Inverse Trigonometric Functions Class 12 MCQs Questions with Answers
Inverse Trigonometric Functions Class 12 MCQ Question. 1.
The value of sin-1(cos \(\frac {3π}{5}\)) is ……………
(A) \(\frac {π}{10}\)
(B) \(\frac {3π}{5}\)
(C) \(\frac {π}{10}\)
(D) \(\frac {-3π}{5}\)
Answer:
(C) \(\frac {π}{10}\)
Explanation:
= sin -1\(\left[\cos \left(\frac{3 \pi}{5}\right)\right]\)
= sin -1\(\left[\cos \left(\frac{\pi}{2}+\frac{\pi}{10}\right)\right]\)
= sin -1\(\left(-\sin \frac{\pi}{10}\right)\) [∴ cos (\(\frac {π}{2}\) + x) = – sinx ]
= sin -1\(\left(\sin \frac{\pi}{10}\right)\) [∵ sin-1 (x) = – sin-1 x ]
= \(\frac {π}{10}\)[∴sin-1(sin x) = x,x ∈\(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
Inverse Trigonometry Class 12 MCQ Chapter 2 Question 2.
The value of tan \(\left[\frac{1}{2} \cos ^{-1}\left(\frac{\sqrt{5}}{3}\right)\right]\) is
(A) \(\frac{3+\sqrt{5}}{2}\)
(B) \(\frac{3-\sqrt{5}}{2}\)
(C) \(\frac{-3+\sqrt{5}}{2}\)
(D) \(\frac{-3-\sqrt{5}}{2}\)
Answer:
(B) \(\frac{3-\sqrt{5}}{2}\)
Explanation:
x = tan \(\left[\frac{1}{2} \cos ^{-1}\left(\frac{\sqrt{5}}{3}\right)\right]\)
Let cos-1\(\frac{\sqrt{5}}{3}\) = θ
cos θ = \(\frac{\sqrt{5}}{3}\)
⇒ x = tan \(\frac {1}{2}\) θ
⇒ x = \(\frac{\sin \frac{\theta}{2}}{\cos \frac{\theta}{2}}\)
∵ sin \(\frac {θ}{2}\) = \(\frac{\sqrt{1-\frac{\sqrt{5}}{3}}}{\sqrt{2}}\)
Cos \(\frac {θ}{2}\) = \(\frac{\sqrt{1+\frac{\sqrt{5}}{3}}}{\sqrt{2}}\)
x = \(\frac{\sqrt{1-\frac{\sqrt{5}}{3}}}{\sqrt{1+\frac{\sqrt{5}}{3}}}\)
= \(\frac{\sqrt{3-\sqrt{5}}}{\sqrt{3+\sqrt{5}}}\)
= \(\frac{\sqrt{3-\sqrt{5}}}{\sqrt{3+\sqrt{5}}} \times \frac{\sqrt{3-\sqrt{5}}}{\sqrt{3-\sqrt{5}}}\)
= \(\frac{3-\sqrt{5}}{\sqrt{(3)^{2}-(\sqrt{5})^{2}}}\)
= \(\frac{3-\sqrt{5}}{\sqrt{9-5}}\)
= \(\frac{3-\sqrt{5}}{2}\)
![]()
MCQ Of Inverse Trigonometry Class 12 Chapter 2 Question 3.
Which of the following is the principal value branch of cos x?
(A) \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
(B) \(\left[0, \frac{\pi}{2}\right]\)
(C) [0,π]
(D) (0,π) – \(\left\{\frac{\pi}{2}\right\}\)
Answer:
(C) [0,π]
Explanation:
As we know that the principal value of cos-1 x is [0, π]
y = cos-1x
Inverse Trigonometric Functions MCQ Chapter 2 Question 4.
Which of the following is the principal value branch of cosec-1x?
(A) \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
(B) [0,π] – \(\left\{\frac{\pi}{2}\right\}\)
(C) \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
(D) \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – {0}
Answer:
(D) \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – {0}
Explanation:
As we know that the principal value of cosec-1 x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – {0}
y = cosec-1 x
Class 12 Maths Chapter 2 MCQ Question 5.
The value of sin-1 \(\left[\cos \left(\frac{33 \pi}{5}\right)\right]\) is
(A) \(\frac{3 \pi}{5}\)
(B) \(\frac{-7 \pi}{5}\)
(C) \(\frac{\pi}{10}\)
(D) \(\frac{-\pi}{10}\)
Answer:
(D) \(\frac{-\pi}{10}\)
Explanation:
= sin-1 \(\left[\cos \left(\frac{\pi}{2}+\frac{\pi}{10}\right)\right]\)
= sin-1\(\left(-\sin \frac{\pi}{10}\right)\) [∵ cos \(\left(\frac{\pi}{2}+x\right)\) = -sin x]
= sin-1[sin \(\frac {π}{10}\)][∵sin-1(-x) = – sin-1 x]
= \(-\frac{\pi}{10}\) [∵sin-1(sin x) = x,x ∈\(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)]
MCQ On Inverse Trigonometric Functions Chapter 2 Question 6.
The domain of function cos-1 (2x – 1) is
(A) [0,1]
(B) [-1,1]
(C) [-1,1]
(D) [0,π]
Answer:
(A) [0,1].
Explanation:
We have cos-1(2x – 1)
⇒ -1 ≤ 2x – 1 ≤ 1
⇒ 0 ≤ 2x ≤ 2
⇒ 0 ≤ x ≤ 1
⇒ ∈[0,1]
![]()
MCQ On Inverse Trigonometric Functions Class 12 Question 7.
The value of cos-1(cos \(\frac {3π}{2}\)) is
(A) \(\frac {π}{2}\)
(B) \(\frac {3π}{2}\)
(C) \(\frac {5π}{2}\)
(D) \(\frac {7π}{2}\)
Answer:
(A) \(\frac {π}{2}\)
Explanation:
We have,
cos-1(cos \(\frac {3π}{2}\)) = cos-1[cos(2π – \(\frac {π}{2}\))]
[∵ cos (cos \(\frac {3π}{2}\)) = cos \(\frac {π}{2}\)]
= cos-1 cos \(\frac {π}{2}\) = \(\frac {π}{2}\)
[∴cos-1(cos x) = x,x∈[0,π]]
MCQ Inverse Trigonometry Class 12 Chapter 2 Question 8.
The value of expression 2 sec-1 2 + sin-1\(\frac {1}{2}\) is
(A) \(\frac {π}{6}\)
(B) \(\frac {5π}{6}\)
(C) \(\frac {7π}{6}\)
(D) 1
Answer:
(B) \(\frac {5π}{6}\)
Explanation:
We have,
2 sec-1 + sin-1(\(\frac {1}{2}\))
= 2 sec-1 sec \(\frac {π}{3}\) + sin-1(sin x) = x]
= sec-1 (sec x) = x and sin-1(sin x ) = x]
= \(\frac {4π + π}{6}\)
= \(\frac {5π}{6}\)
Inverse Trigonometry MCQs Chapter 2 Question 9.
What is the value of sec2(tan-1)
(A) 1
(B) 4
(C) 5
(D) 3
Option
(C) 5
Explanation:
sec2(tan-1 2) sec2(sec-1\(\sqrt{1+2^{2}}\))
sec2(sec-1\(\sqrt{{2}}\))
= (\(\sqrt{{2}}\))2
= 5
Class 12 Inverse Trigonometry MCQ Chapter 2 Question 10.
The principal value of
cos -1\(\frac {1}{2}\) + 2 sin-1\(\frac {1}{2}\) + tan-1\(\frac {1}{2}\) is …………
(A) \(\frac {π}{3}\)
(B)\(\frac {π}{6}\)
(C) \(\frac {4π}{3}\)
(D) \(\frac {3π}{4}\)
Answer:
(C) \(\frac {4π}{3}\)
Explanation :
= cos-1\(\frac {1}{2}\) + 2 sin-1 \(\frac {1}{2}\) + 4 tan-1 \(\left(\frac{1}{\sqrt{3}}\right)\)
= cos-1(cos\(\frac {π}{3}\)) + 2 sin-1(sin \(\frac {π}{6}\)) + 4 tan-1(tan \(\frac {π}{2}\))
= \(\frac {π}{3}\) + 2 x \(\frac {π}{6}\) + 4 x \(\frac {π}{6}\)
= \(\frac{2 \pi+2 \pi+4 \pi}{6}\)
= \(\frac {8π}{6}\)
= \(\frac {4π}{3}\)
![]()
Inverse Trigonometry MCQ Chapter 2 Class 12 Question 11.
The principal value of cot-1\((-\sqrt{3})\) is
(A) \(\frac {4π}{3}\)
(B) \(\frac {π}{2}\)
(C) \(\frac {π}{4}\)
(D) \(\frac {π}{3}\)
Answer:
(A) \(\frac {4π}{3}\)
Explanation:
Let cot-1 (\(\frac {1}{2}\)) = θ
⇒ cot θ = – \(\sqrt{3}\)
⇒ cot θ = – cot \(\frac {π}{6}\)
= cot π – \(\frac {π}{6}\)
⇒ cot θ = cot \(\frac {5π}{6}\)
θ = \(\frac {5π}{6}\) ∈ (0,π)
∴ Principal value of cot-1(\((-\sqrt{3})\)) is \(\frac {5π}{6}\)
Inverse Trigonometric Functions MCQ Pdf Chapter 2 Question 12.
Domain of sirix is:
(A) (-1,∞)
(B) (-1,1)
(C) (-1, 1)
(D) None of these.
Answer:
(B) (-1,1)
Explanation:
Domain of sin-1 x is [-1, 1]
MCQ Questions For Inverse Trigonometry Class 12 Question 13.
Range of cos-1 x is:
(A) [0, \(\frac {π}{2}\)]
(B) [-\(\frac {π}{2}\) , \(\frac {π}{2}\) ]
(C) [-\(\frac {π}{2}\) , \(\frac {3π}{2}\) ]
(D) [0,π]
Answer:
(D) [0,π]
Explanation:
The branch with range (0, π) is called the pñncipal value branch of the function cas-1x.
Class 12 Maths Chapter 2 MCQ Questions Question 14.
Domain of sec1x is:
(A) R -(-1, 1)
(B) R
(C) (-1,1]
(D) R-(0, 1)
Answer:
(A) R -(-1, 1)
MCQ Of Chapter 2 Maths Class 12 Question 15.
The value of tan-1 (\((-\sqrt{3})\)) – sec-1(-2) is:
(A) π
(B) – \(\frac {π}{3}\)
(C) \(\frac {π}{3}\)
(D) \(\frac {2π}{3}\)
Answer:
(B) – \(\frac {π}{3}\)
Explanation:
tan-1 – sec-1(-2)
= \(\frac {π}{3}\) – \(\frac {2π}{3}\) = – \(\frac {π}{3}\)
Assertion And Reason Based MCQs (1 Mark each)
Directions: In the following Questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
(A) Both A and R are true and R is 11w correct explanation of A
(B) Both A and R are true but R is NOT the correct explanation of A
(C) A is true but R is false
(D) Ais false and R is True
![]()
Class 12 Maths Ch 2 MCQ Question 1.
Assertion (A): sin-1 (sin \(\frac {2π}{3}\) ) = \(\frac {2π}{3}\)
Reason (R): sin-1 (sin θ) = θ, if θ ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Answer:
(D) Ais false and R is True
Explanation:
The pnncipal value branch of sin-1 is \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Let x = sin θ ⇒ θ sin-1x
sin-1(sin θ) = sin-1 = θ
sin-1’(sin θ) = θ, if θ ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Hence R is true.
Sin-1(sin \(\frac {2π}{3}\)) ≠ \(\frac {2π}{3}\),since \(\frac {2π}{3}\) ☐ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Hence A is false.
MCQ Of Inverse Trigonometric Functions Chapter 2 Question 2.
Assertion (A): Range of tan-1 x is \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Reason (R): Domain of tan-1 x is R.
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A
Explanation:
Domain of tan x is the set {x: x ∈ R and x ≠ (2n+ 1) \(\frac {π}{2}\), n∈Z} and Range is R.
⇒ tan x is not defined for odd multiples of \(\frac {π}{2}\)
If we restrict the domain of tangent function to \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\), then it is one-one and onto with its
range as R. Actually tan x restricted to any of the intervals
\(\left(\frac{-3 \pi}{2}, \frac{-\pi}{2}\right),\left(\frac{-\pi}{2}, \frac{\pi}{2}\right),\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)etc., is
bijective and its range is R.
Thus tan-1 x can be defined as a function whose domain is R and range could be any of the intervals \(\left(\frac{-3 \pi}{2}, \frac{-\pi}{2}\right),\left(\frac{-\pi}{2}, \frac{\pi}{2}\right),\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)and
soon.
∴ Both A and R are true but R is not correct explanation of A.
MCQs On Inverse Trigonometric Functions Chapter 2 Question 3.
Assertion (A): Principal value of sin-1 \(\left(\frac{1}{\sqrt{2}}\right)\) is \(\frac {π}{4}\)
Reason (R): Principal value of cot-1 \(\left(\frac{1}{\sqrt{3}}\right)\) is \(\frac {π}{3}\)
Answer:
(C) A is true but R is false
Explanation:
sin-1 \(\left(\frac{1}{\sqrt{2}}\right)\) = sin (sin \(\frac {π}{4}\)) = \(\frac {π}{4}\)
cot-1 \(\left(\frac{-1}{\sqrt{3}}\right)\) = y
cot y = \(\left(\frac{-1}{\sqrt{3}}\right)\)
= – cot \(\frac {π}{3}\)
= cot (π – \(\frac {π}{3}\))
= cot (\(\frac {π}{3}\))
cot-1\(\left(\frac{-1}{\sqrt{3}}\right)\) = \(\frac {2π}{3}\)
Hence Assertion is correct and Reason is incorrect.
MCQ On Inverse Trigonometry Class 12 Chapter 2 Question 4.
Assertion (A): Range of cot-1 x is (0, π)
Reason (R): Domain of tan-1 x is R.
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A
MCQ Class 12 Maths Chapter 2 Question 5.
Assertion (A): Principal value of cos-1(1) is π
Reason (R): Value of cos 0° is 1
Answer:
(D) Ais false and R is True
Explanation:
in case of Assertion:
cos-1(1) = y
cos y = 1
cos y = cos 0° [∴cos 0° = 1]
∴y = 0
⇒ Principal value of cos-1 (1) is 0
Hence Assertion is in correct.
Reason is correct.
![]()
Case-Based MCQs
Attempt any four sub-parts from each Question.
Each sub-part carries 1 mark.
I. Read the following text and answer the following Questions on the basis of the same:
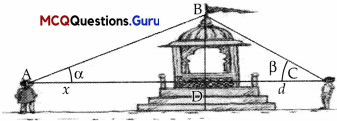
Two men on either side of a temple of 30 metres high observe its top at the angles of elevation a and (3 respectively, (as shown in the figure above). The distance between the two men is 40\((\sqrt{3})\) metres and the distance between the first person A and the temple is 30\((\sqrt{3})\) meters.
Ch 2 Maths Class 12 MCQ Question 1.
∠CAB = α =
(A) sin-1\(\left(\frac{2}{\sqrt{3}}\right)\)
(B) sin -1 \(\left(\frac{1}{2}\right)\)
(C) sin -1 (2)
(D) sin -1 \(\left(\frac{\sqrt{3}}{2}\right)\)
Answer:
(B) sin -1 \(\left(\frac{1}{2}\right)\)
Explanation:
In ∆ BDA
sin α = \(\frac {BD}{AB}\)
AB2 = AD2 + BD2
= (30\((30 \sqrt{3})^{2}\))2 +(30)2
= (60)2
AB = 60m
Now, sin α = \(\frac {30}{60}\)
sin α = \(\frac {1}{2}\)
i.e. ∠CAB = α = sin-1\(\frac {1}{2}\)
MCQ Of Maths Class 12 Chapter 2 Question 2.
∠CAB = α =
(A) cos-1(\(\frac {1}{5}\))
(B) cos-1(\(\frac {2}{5}\))
(C) cos-1(\(\left(\frac{\sqrt{3}}{2}\right)\))
(D) cos-1(\(\frac {4}{5}\))
Answer:
(C) cos-1(\(\left(\frac{\sqrt{3}}{2}\right)\))
Explanation:
In ∆ BDA
cos α = \(\frac {AD}{AB}\)
cos α = \(\frac{30 \sqrt{3}}{60}\)
α = cos-1 \(\left(\frac{\sqrt{3}}{2}\right)\)
∴ ∠CAB = α = cos-1 \(\left(\frac{\sqrt{3}}{2}\right)\)
MCQ Questions Of Inverse Trigonometric Functions Chapter 2 Question 3.
∠BCA = β =
(A) tan-1(\(\frac {1}{2}\))
(B) tan-1 (2)
(C) tan-1\(\left(\frac{1}{\sqrt{3}}\right)\)
(D) tan-1\((\sqrt{3})\)
Answer:
(D) tan-1\((\sqrt{3})\)
Explanation:
DC = AC – AD
= 4o\((\sqrt{3})\) -3o\((\sqrt{3})\)
= 10\((\sqrt{3})\)m
In ABDC
tan β = \(\frac {BD}{DC}\) ≠ \(\frac{30}{10 \sqrt{3}}\) = \((\sqrt{3})\)
∠BCA = β = tan-1\((\sqrt{3})\)
![]()
Question 4.
∠ABC =
(A) \(\frac{\pi}{4}\)
(B) \(\frac{\pi}{6}\)
(C) \(\frac{\pi}{2}\)
(D) \(\frac{\pi}{3}\)
Answer:
(C) \(\frac{\pi}{2}\)
Explanation:
Since
Sin α = \(\frac {1}{2}\)
i.e Sin α = sin 30°
we have
tan β = \((\sqrt{3})\)
tan β = tan 60°
∴ β = 60°
Now, In ∆ABC
∠ABC + ∠BCA + ∠CAB = 180°
∠ABC + 60° + 30° = 180°
∠ABC = 90°
∴ ABC = \(\frac {π}{2}\)
Question 5.
Domain and Range of cos1 X
(A) (-1, 1), (0, π)
(B) [-1, 1), (0, π)
(C) [-1, 1), [0, π]
(D) (-1, 1), \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\)
Answer:
(C) [-1, 1), [0, π]
II. Read the following text and answer the following Questions on the basis of the same: In the school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to tan-1\(\frac {1}{2}\) and tan-1 \(\frac {1}{3}\) respectively

Question 1.
The value of sin A is
(A) \(\frac {1}{2}\)
(B) \(\frac {1}{3}\)
(C) \(\frac{1}{\sqrt{5}}\)
(D) \(\frac{2}{\sqrt{5}}\)
Answer:
(C) \(\frac{1}{\sqrt{5}}\)
Explanation:
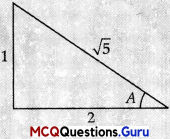
A = tan-1 \(\frac {1}{2}\)
tan A = \(\frac {1}{2}\)
∴ sin A = \(\frac{1}{\sqrt{5}}\)
Question 2.
Cos (A + B + C) = ……………..
(A) -1
(B) 0
(C) -1
(D) \(\frac {1}{2}\)
Answer:
-1
Explanation:
Explanation: Since ABC is a triangle,
A + B + C = 180°
cos(A + B + C) = cos 180° = -1
![]()
Question 3.
If B = cos-1x, then x = ………….
(A) \(\frac{1}{\sqrt{5}}\)
(B) \(\frac{3}{\sqrt{10}}\)
(C) \(\frac{1}{\sqrt{10}}\)
(D) \(\frac{2}{\sqrt{5}}\)
Answer:
(B) \(\frac{3}{\sqrt{10}}\)
Explanation:
B = tan-1 \(\frac {1}{3}\)
⇒ tan B = \(\frac {1}{3}\)
cos B = \(\frac{3}{\sqrt{10}}\)
B = cos-1\(\frac{3}{\sqrt{10}}\)
⇒ x = \(\frac{3}{\sqrt{10}}\)
![]()
Question 4.
If B = sin-1x, then x = ………….
(A) \(\frac{1}{\sqrt{5}}\)
(B) \(\frac{3}{\sqrt{10}}\)
(C) \(\frac{1}{\sqrt{10}}\)
(D) \(\frac{2}{\sqrt{5}}\)
Answer:
(A) \(\frac{1}{\sqrt{5}}\)
Explanation:
A = tan-1\(\frac {1}{2}\)
⇒ tan A = \(\frac {1}{2}\)
∴ Sin A = \(\frac{1}{\sqrt{5}}\)
A = Sin-1 \(\frac{1}{\sqrt{5}}\)
⇒ x = \(\frac{1}{\sqrt{5}}\)
Question 5.
The third angle, ∠C = …………..
(A) \(\frac {π}{4}\)
(B) \(\frac {π}{2}\)
(C) \(\frac {π}{3}\)
(D) \(\frac {3π}{4}\)
Answer:
(D) \(\frac {3π}{4}\)
Explanation:
∠C = π – (A + B)
= π – \(\frac {π}{4}\)
= \(\frac {3π}{4}\)
III. Read the following text and answer the following Questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Question 1.
Principal value of sin’ () is
(A) \(\frac {π}{6}\)
(B) \(\frac {π}{3}\)
(C) \(\frac {π}{4}\)
(D) \(\frac {π}{2}\)
Answer:
(A) \(\frac {π}{6}\)
Explanation:
Sin-1\(\left(\frac{1}{2}\right)\) = y
Sin y = \(\frac {1}{2}\)
Principal value branch of Sin-1 is \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
and sin \(\frac {π}{6}\) = \(\frac {1}{2}\)
Principal vlaue of sin-1\(\frac {1}{2}\) is \(\frac {π}{6}\)
![]()
Question 2.
Principal value of tan-1(I)
(A) \(\frac {π}{4}\)
(B) \(\frac {π}{2}\)
(C) π
(D) \(\frac {π}{3}\)
Answer:
(A) \(\frac {π}{4}\)
Explanation:
tan-1 = tan-1(tan \(\frac {π}{4}\) )
= \(\frac {π}{4}\)
Question 3.
Principal value of cot-1\((\sqrt{3})\) is:
(A) \(\frac {π}{3}\)
(B) π
(C) \(\frac {π}{6}\)
(D) \(\frac {π}{2}\)
Answer:
(C) \(\frac {π}{6}\)
Explanation:
cot-1\((\sqrt{3})\) = cot-1 (cot \(\frac {π}{6}\)) = \(\frac {π}{6}\)
Question 4.
Principal value of sin-1 (1) + sin-1\(\left(\frac{1}{\sqrt{2}}\right)\) is
(A) 2π
(B) π
(C) \(\frac {3π}{4}\)
(D) \(\frac {π}{3}\)
Answer:
(C) \(\frac {3π}{4}\)
Explanation:
sin-1 + sin-1\(\left(\frac{1}{\sqrt{2}}\right)\) = \(\frac{\pi}{2}+\frac{\pi}{4}\)
= \(\frac {3π}{4}\)
Question 5.
Principal value of 2cos-1 (1) + 5tan-1 (1) is:
(A) \(\frac {3π}{4}\)
(B) \(\frac {π}{4}\)
(C) \(\frac {π}{2}\)
(D) \(\frac {5π}{4}\)
Answer:
(D) \(\frac {5π}{4}\)
Explanation:
2 cos-1(1) + 5 tan-1 (1)
= 2 x 0 + 5 x \(\frac {π}{4}\)
= \(\frac {5π}{4}\)




