Integrals Class 12 MCQs Questions with Answers
Integration MCQ Class 12 Maths Chapter 7 Question 1.
\(\int \frac{\cos 2 x-\cos 2 \theta}{\cos x-\cos \theta}\) dx is equal to
(A) 2.(sin x + x cos θ) + C
(B) 2(sin x – x cos θ) + C
(C) 2(sin x + 2x cos θ) + C
(D) 2(sin x – 2x cos θ) + C
Answer:
(A) 2.(sin x + x cos θ) + C
Explanation:
I = \(\int \frac{\cos 2 x-\cos 2 \theta}{\cos x-\cos \theta} d x\)
= \(\int \frac{\left(2 \cos ^{2} x-1-2 \cos ^{2} \theta+1\right)}{\cos x-\cos \theta} d x\)
= \(2 \int \frac{(\cos x+\cos \theta)(\cos x-\cos \theta)}{(\cos x-\cos \theta)} d x\)
= 2\(\int(\cos x+\cos \theta) d x\)
= 2 sin x + 2 cos θ + C
MCQ On Integration Class 12 Chapter 7 Question 2.
The value of \(\int_{-\pi / 2}^{\pi / 2}\left(x^{3}+x \cos x+\tan ^{5} x+1\right) d x\) is
(A) O
(B) 2
(C) π
(D) 1
Answer:
(C) π
Explanation:
Let,
= \(\int_{-\pi / 2}^{\pi / 2}\left(x^{3}+x \cos x+\tan ^{5} x+1\right) d x\)
= \(\int_{-\pi / 2}^{\pi / 2} x^{3} d x+\int_{-x / 2}^{\pi / 2} x \cos x+\int_{-\pi / 2}^{\pi / 2} \tan ^{5} x d x+\) + \(\int_{-\pi / 2}^{\pi / 2} 1 \cdot d x\)
it is know that if f(x) is an even function, then \(\int_{-\Omega}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x\)
and if f(x)is an odd function, then
= \(\int_{-a}^{a} f(x) d x=0\)
∴ I = 0 + 0 + 0 + 2\(\int_{0}^{\pi / 2} 1 \cdot d x\)
= \(2[x]_{0}^{\pi / 2}=\frac{2 \pi}{2}=\pi\)
= 2 sin x + 2x cos θ + C
Integration MCQ Questions Class 12 Chapter 7 Question 3.
\(\int \frac{d x}{e^{x}+e^{-x}}\) is equal to ‘
(A) tan-1 (ex) + C
(B) tan-1(e-x) + C
(C) log(ex – e-x) + C
(D) log (ex + e-x) + C
Answer:
(A) tan-1 (ex) + C
Explanation:
Let
I = \(2[x]_{0}^{\pi / 2}=\frac{2 \pi}{2}=\pi\)
= \(2[x]_{0}^{\pi / 2}=\frac{2 \pi}{2}=\pi\)
Also, let ex = t
ex dx = dt
I = \(\int \frac{d t}{1+t^{2}}\)
= tan-1 t + C
= tan-1 (ex) + C
![]()
MCQ On Integration Class 12 Question 4.
\(\int \frac{\cos 2 x}{(\sin x+\cos x)^{2}}\) is equal to
(A) \(\frac{-1}{\sin x+\cos x}+C\)
(B) \(\log |\sin x+\cos x|+C\)
(C) \(\log |\sin x-\cos x|+C\)
(D) \(\frac{1}{(\sin x+\cos x)^{2}}\)
Answer:
(B) \(\log |\sin x+\cos x|+C\)
Explanation:
Let
I = \(\frac{\cos 2 x}{(\cos x+\sin x)^{2}}\)
I = \(\int \frac{\cos ^{2} x-\sin ^{2} x}{(\cos x+\sin x)^{2}} d x\)
= \(\int \frac{(\cos x+\sin x)(\cos x-\sin x)}{(\cos x+\sin x)^{2}} d x\)
= \(\int \frac{\cos x-\sin x}{\cos x+\sin x} d x\)
Let cos x + sin x = t
⇒ (cos x – sin x) dx = dt
⇒ I = \(\int \frac{d t}{t}\)
= log |t| + C
= log |cos x = sin x |+ C
Integration MCQs Class 12 Chapter 7 Question 5.
if f(a + b – x) = f(x), then \(\int_{a}^{b} x f(x) d x\) is equal to
(A) \(\frac{a+b}{2} \int_{a}^{b} f(b-x) d x\)
(B) \(\frac{a+b}{2} \int_{a}^{b} f(b+x) d x\)
(C) \(\frac{b-a}{2} \int_{a}^{b} f(x) d x\)
(D) \(\frac{a+b}{2} \int_{a}^{b} f(x) d x\)
Answer:.
(D) \(\frac{a+b}{2} \int_{a}^{b} f(x) d x\)
Explanation:
Let
I = \(\int_{a}^{b} x f(x) d x\)
I = \(\int_{a}^{b}(a+b-x) f(a+b-x) d x\) [∵\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(a+b-x) d x\)]
⇒ I = \(\int_{a}^{b}(a+b-x) f(x) d x\)
⇒I = \((a+b) \int_{a}^{b} f(x) d x-I\) – I [Using Equestion(i)]
⇒ I + I = \((a+b) \int_{a}^{b} f(x) d x\)
⇒ 2I = \((a+b) \int_{a}^{b} f(x) d x\)
⇒ I = \(\left(\frac{a+b}{2}\right) \int_{a}^{b} f(x) d x\)
MCQ Of Integration Class 12 Chapter 7 Question 6.
The Value of \(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right) d x\) is
(A) 1
(B) 0
(C) -1
(D) \(\frac {π}{4}\)
Answer:
(B) 0
Explanation:
Let
⇒ I = \(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right) d x\)
⇒ I = \(\int_{0}^{1} \tan ^{-1}\left(\frac{x-(1-x)}{1+x(1-x)}\right) d x\)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1} x-\tan ^{-1}(1-x)\right] d x\) ……….(i)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1}(1-x)-\tan ^{-1}(1-1+x)\right] d x\)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1}(1-x)-\tan ^{-1}(x)\right] d x\)
⇒ I = \(\int_{0}^{1}\left[\tan ^{-1}(1-x)-\tan ^{-1}(x)\right] d x\) ………(ii)
Adding equestion(i) and (ii), we obtained
2I = \(\int_{0}^{1}\left(\tan ^{-1} x+\tan ^{-1}(1-x)\right.\) – \(\left.-\tan ^{-1}(1-x)-\tan ^{-1} x\right) d x\)
⇒ I = 0
![]()
MCQs On Integration Class 12 Chapter 7 Question 7.
\(\int_{0}^{1} \tan ^{-1}\left(\frac{2 x-1}{1+x-x^{2}}\right) d x\) is equal to
(A) \(\sin (b-a) \log \left|\frac{\sin (x – b)}{\sin (x – a)}\right|+C\)
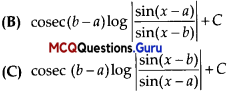
(D) \(\sin (b-a) \log \left|\frac{\sin (x – a)}{\sin (x – b)}\right|+C\)
Answer:.
Option (C) is correct.
Explanation:
Let
I = \(\int \frac{d x}{\sin (x-a) \sin (x-b)}\)
= \(\frac{1}{\sin (b-a)} \int \frac{\sin (b-a)}{\sin (x-a) \sin (x-b)} d x\)
= \(\frac{1}{\sin (b-a)} \int \frac{\sin (x-a-x+b)}{\sin (x-a) \sin (x-b)} d x\)
= \(\frac{1}{\sin (b-a)} \int \frac{\sin \{(x-a)-(x-b)\}}{\sin (x-a) \sin (x-b)} d x\)
sin (x – a) cos (x – b) –
= \(\frac{1}{\sin (b-a)} \int \frac{\cos (x-a) \sin (x-b)}{\sin (x-a) \sin (x-b)} d x\)
= \(\frac{1}{\sin (b-a)} \int[\cot (x-b)-\cot (x-a)] d x\)
= \(\frac{1}{\sin (b-a)}[\log |\sin (x-b)|-\log |\sin (x-a)|]+C\)
![]()
Integration MCQ With Answers Pdf Class 12 Chapter 7 Question 8.
\(\int \sqrt{1+x^{2}} d x\) is equal to
(A) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left|\left(x+\sqrt{1+x^{2}}\right)\right|+C\)
(B) \(\frac{2}{3}\left(1+x^{2}\right)^{3 / 2}+C\)
(C) \(\frac{2}{3} x\left(1+x^{2}\right)^{3 / 2}+C\)
(D) \(\frac{x^{2}}{2} \sqrt{1+x^{2}}+\frac{1}{2} x^{2} \log \left(x+\sqrt{1+x^{2}}\right)+C\)
Answer:
(A) \(\frac{x}{2} \sqrt{1+x^{2}}+\frac{1}{2} \log \left|\left(x+\sqrt{1+x^{2}}\right)\right|+C\)
Explanation:
it is known that,
\(\int \sqrt{a^{2}+x^{2}} d x=\frac{x}{2} \sqrt{a^{2}+x^{2}}\) + \(+\frac{a^{2}}{2} \log \left|x+\sqrt{x^{2}+a^{2}}\right|+C\)
\(\int \sqrt{1+x^{2}} d x=\frac{x}{2} \sqrt{1+x^{2}}\) + \(+\frac{1}{2} \log \left|x+\sqrt{1+x^{2}}\right|+C\)
MCQ Integration Class 12 Chapter 7 Question 9.
\(\int \frac{x d x}{(x-1)(x-2)}\) is equal to
(A) \(\log \left|\frac{(x-1)^{2}}{x-2}\right|+C\)
(B) \(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)
(C) \(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)
(D) \(\log |(x-1)(x-2)|+C\)
Answer:
(B) \(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)
Explanation:
Let
\(\frac{x}{(x-1)(x-2)}=\frac{A}{(x-1)}+\frac{B}{(x-2)}\)
x = A(x – 2) + B (x – 1) ………..(i)
Substituting x = 1 and 2 in Equestion (i), we obtained
A = -1 and B = 2
∴ \(\frac{x}{(x-1)(x-2)}=-\frac{1}{(x-1)}+\frac{2}{(x-2)}\)
\(\int \frac{x}{(x-1)(x-2)} d x=\int\left\{\frac{-1}{(x-1)}+\frac{2}{(x-2)}\right\} d x\)
= -log |x – 1| + 2 log |x – 2| + C
\(\log \left|\frac{(x-2)^{2}}{x-1}\right|+C\)
Integral MCQ Questions Class 12 Chapter 7 Question 10.
If f(x) = \(\int_{0}^{x} t \sin t d t\), then f'(x) is
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
Answer:
(B) x sin x
Explanation:
f(x) = \(\int_{0}^{x} t \sin t d t\)
Integrating by parts, we obtain
f(x) = \(t \int_{0}^{x} \sin t d t-\int_{0}^{x}\left\{\left(\frac{d}{d t} t\right) \int \sin t d t\right\} d t\)
= \([t(-\cos t)]_{0}^{x}-\int_{0}^{x}(-\cos t) d t\)
= [-t cost + sin t]x0
= -x cos x + sin x
= f'(x) = -[{x(- sin x)}+cos x] + cos x
x sin x – cos x + cos x
= x sin x
![]()
Integration MCQ Class 12 Chapter 7 Question 11.
\(\int \tan ^{-1} \sqrt{x} d x\) is equal to
(A) (x + 1)tan-1\(\sqrt{x}-\sqrt{x}\) + C
(B) x tan-1\(\sqrt{x}-\sqrt{x}\) + C
(C) \(\sqrt{x}-\sqrt{x}\) tan-1\(\sqrt{x}\) + C
(D) \(\sqrt{x}\) – (x + )tan \(\sqrt{x}\) + C
Answer:
(A) (x + 1)tan-1\(\sqrt{x}-\sqrt{x}\) + C
Explanation:
Let,
I = \(\int 1 \cdot \tan ^{-1} \sqrt{x} d x\)
= tan-1 \(\sqrt{x} \cdot x-\frac{1}{2} \int \frac{1}{(1+x)} \cdot \frac{2}{\sqrt{x}} d x\)
=x tan-1 \(\sqrt{x}-\frac{1}{2} \int \frac{2}{\sqrt{x}(1+x)} d x\)
Put x = t2
⇒ dx = 2t dt
∴ I = x tan-1\(\sqrt{x}\) – \(\int \frac{t}{t\left(1+t^{2}\right)} d t\)
x = tan-1\(\sqrt{x}\) – \(\int \frac{t^{2}}{1+t^{2}} d t\)
= tan-1\(\sqrt{x}\) – \(\int\left(1-\frac{1}{1+t^{2}}\right) d t\)
= tan-1\(\sqrt{x}\) – \(\int\left(1-\frac{1}{1+t^{2}}\right) d t\)
= \(x \tan ^{-1} \sqrt{x}-\sqrt{x}+\tan ^{-1} t+C\)
= \(x \tan ^{-1} \sqrt{x}-\sqrt{x}+\tan ^{-1} \sqrt{x}+C\)
= \((x+1) \tan ^{-1} \sqrt{x}-\sqrt{x}+C\)
Integral MCQ Class 12 Chapter 7 Question 12.
\(\int x^{2} e^{x^{3}} d x\) is equal to
(A) \(\frac{1}{3} e^{x^{3}}+C\)
(B) \(\frac{1}{3} e^{x^{2}}+C\)
(C) \(\frac{1}{2} e^{x^{3}}+C\)
(D) \(\frac{1}{2} e^{x^{2}}+C\)
Answer:
(A) \(\frac{1}{3} e^{x^{3}}+C\)
Explanation:
Let,
I = \(\int x^{2} e^{x^{3}} d x\)
Also, let x3 = t
⇒ 3 x2 dx = dt
⇒ I = \(\frac{1}{3} \int e^{t} d t\)
= \(\frac{1}{3}\)(et) + C
= \(\frac{1}{3} e^{x^{3}}+C\)
Integration MCQs Class 12 Chapter 7 Question 13.
\(\int e^{x} \sec x(1+\tan x) d x\) is equal to
(A) ex cos x + C
(B) ex sec x + C
(C) ex sin x + C
(D) ex tan x + C
Answer:
(B) ex sec x + C
Explanation:
\(\int e^{x} \sec x(1+\tan x) d x\)
Let
I = \(\int e^{x} \sec x(1+\tan x) d x=\int e^{x}(\sec x+\sec x \tan x) d x\)
Also, let sec x = f(x) ⇒sec x tan x = f'(x)
It is known that, \(\int e^{x}\left\{f(x)+f^{\prime}(x)\right\} d x=e^{x} f(x)+C\)
∴ ex sec x + C
Integration Class 12 MCQ Chapter 7 Question 14.
\(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin ^{2} x \cos ^{2} x}\) dx is equal to
(A) tan x + cot x + C
(B) tan x + cosec x + C
(C) -tan x + cot x + C
(D) tan x + sec x + C
Answer:
(A) tan x + Cot x + C
Explanation:
\(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x=\int\left(\frac{\sin ^{2} x}{\sin ^{2} x \cos ^{2} x}-\frac{\cos ^{2} x}{\sin ^{2} x \cos ^{2} x}\right) d x\)
= ![]()
= tan x + cot x+ C
MCQ Of Integration Chapter 7 Class 12 Question 15.
\(\int \frac{d x}{\sin ^{2} x \cos ^{2} x}\) equal to
(A) tan x + cot x + C
(B) tan x – cot x + C
(C) tan x cot x + C
(D) tan x – cot 2x + C
Answer:
(B) tan x – cot x + C
Explanation:
Let
I = \(\int \frac{d x}{\sin ^{2} x \cos ^{2} x}\)
= \(\int \frac{1}{\sin ^{2} x \cos ^{2} x} d x\)
= \(\int \frac{\sin ^{2} x+\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x\)
= \(\int \frac{\sin ^{2} x}{\sin ^{2} x \cos ^{2} x} d x+\int \frac{\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x\)
= ![]()
= tan x – cot x + C
![]()
Question 16.
\(\int \frac{x^{9}}{\left(4 x^{2}+1\right)^{6}} d x\) is equal to
(A) \(\frac{1}{5 x}\left(4+\frac{1}{x^{2}}\right)^{-5}+C\)
(B) \(\frac{1}{5}\left(4+\frac{1}{x^{2}}\right)^{-5}+C\)
(C) \(\frac{1}{10 x}(1+4)^{-5}+C\)
(D) \(\frac{1}{10}\left(\frac{1}{x^{2}}+4\right)^{-5}+C\)
Answer:
(D) \(\frac{1}{10}\left(\frac{1}{x^{2}}+4\right)^{-5}+C\)
Explanation:
I = \(\int \frac{x^{9}}{\left(4 x^{2}+1\right)^{6}} d x\)
= \(\int \frac{x^{9}}{x^{12}\left(4+\frac{1}{x^{2}}\right)^{6}} d x\)
= \(\int \frac{d x}{x^{3}\left(4+\frac{1}{x^{2}}\right)^{6}}\)
put 4 + \(\frac{1}{x^{2}}\) = t
⇒ \(\frac{-2}{x^{3}}\) dx = dt
⇒ \(\frac{-2}{x^{3}}\) dx = –\(\frac{1}{2}\) dt
∴ I = \(\frac{1}{2} \int \frac{d t}{t^{6}}\)
= \(-\frac{1}{2}\left[\frac{t^{-6+1}}{-6+1}\right]+C\)
= \(\frac{1}{10}\left[\frac{1}{t^{5}}\right]+C\)
= \(\frac{1}{10}\left(4+\frac{1}{x^{2}}\right)^{-5}+C\)
Question 17.
\(\frac{1}{x^{2}}\) is equal to
(A) \(x+\frac{x^{2}}{2}+\frac{x^{3}}{3}-\log |1-x|+C\)
(B) \(x+\frac{x^{2}}{2}-\frac{x^{3}}{3}-\log |1-x|+C\)
(C) \(x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\log |1+x|+C\)
(D) \(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\log |1+x|+C\)
Answer:
(D) \(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\log |1+x|+C\)
Explanation:
Let
I = \(\int \frac{x^{3}}{x+1} d x\)
= \(\int\left(\left(x^{2}-x+1\right)-\frac{1}{(x+1)}\right) d x\)
= \(\frac{x^{3}}{3}-\frac{x^{2}}{2}+x-\log |x+1|+C\)
Question 18.
if \(\int \frac{x^{3} d x}{\sqrt{1+x^{2}}}=a\left(1+x^{2}\right)^{3 / 2}+b \sqrt{1+x^{2}}+C\) then
(A) a = \(\frac {1}{3}\), b = 1
(B) a = \(\frac {-1}{3}\), b = 1
(C) a = \(\frac {-1}{3}\), b = -1
(D) a = \(\frac {-1}{3}\), b = -1
Answer:.
(D) a = \(\frac {-1}{3}\), b = -1
Explanation:
Let
I = \(\int \frac{x^{3}}{\sqrt{1+x^{2}}} d x\)
= \(a\left(1+x^{2}\right)^{3 / 2}+b \sqrt{1+x^{2}}+C\)
I = \(\int \frac{x^{3}}{\sqrt{1+x^{2}}} d x\)
= \(\int \frac{x^{2} \cdot x}{\sqrt{1+x^{2}}} d x\)
Put 1 + x2 = t2
⇒ 2x dx = 2t dt
∴ I = \(\int \frac{t\left(t^{2}-1\right)}{t} d t\)
= \(\frac{t^{3}}{3}-t+C\)
= \(\frac{1}{3}\left(1+x^{2}\right)^{3 / 2}-\sqrt{1+x^{2}}+C\)
∴ a = \(\frac {-1}{3}\), b = -1
Question 19.
\(\int_{-\pi / 4}^{\pi / 4} \frac{d x}{1+\cos 2 x}\) is equal to
(A) 1
(B) 2
(C) 3
(D) 4
Answer:
(D) 4
Explanation:
Let
I = \(\int_{-\pi / 4}^{\pi / 4} \frac{d x}{1+\cos 2 x}\)
= \(\int_{-\pi / 4}^{\pi / 4} \frac{d x}{2 \cos ^{2} x}\)
= \(\frac{1}{2} \int_{-\pi / 4}^{\pi / 4} \sec ^{2} x d x\)
= \(\int_{0}^{\pi / 4} \sec ^{2} x d x\)
= \([\tan x]_{0}^{\pi / 4}\)
= 1
Question 20.
\(\int \frac{d x}{x^{2}+2 x+2}\) equals
(A) x tan-1 (x + 1) + C
(B) tan-1 (x + 1) + C
(C) (x + 1) tan-1 + C
(D) tan-1 + C
Answer:
(B) tan-1 (x + 1) + C
Explanation:
\(\int \frac{d x}{x^{2}+2 x+2}=\int \frac{d x}{\left(x^{2}+2 x+1\right)+1}\)
= \(\int \frac{1}{(x+1)^{2}+(1)^{2}} d x\)
= \(\left[\tan ^{-1}(x+1)\right]+C\)
![]()
Question 21.
\(\int \frac{d x}{x^{2}+2 x+2}\) is equal to
(A) \(2 \sqrt{2}\)
(B) \(2(\sqrt{2}+1)\)
(C) 2
(D) \(2(\sqrt{2}-1)\)
Answer:
(D) \(2(\sqrt{2}-1)\)
Explanation:
Let
I = \(\int_{0}^{\pi / 2} \sqrt{1-\sin 2 x} d x\)
= \(\int_{0}^{\pi / 4} \sqrt{(\cos x-\sin x)^{2}} d x\) + \(+\int_{\pi / 4}^{\pi / 2} \sqrt{(\sin x-\cos x)^{2}} d x\)
= \([\sin x+\cos x]_{0}^{\pi / 4}+[-\cos x-\sin x]_{\pi / 4}^{\pi / 2}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-0-1+\left(-0-1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right) \)
= \(2(\sqrt{2}-2)\)
= \(2(\sqrt{2}-1)\)
Question 22.
The anti-derivative of \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)\) equals
(A) \(\frac{1}{3} x^{1 / 3}+2 x^{1 / 2}+C\)
(B) \(\frac{2}{3} x^{2 / 3}+\frac{1}{2} x^{2}+C\)
(C) \(\frac{2}{3} x^{2 / 3}+2 x^{1 / 2}+C\)
(D) \(\frac{3}{2} x^{3 / 2}+\frac{1}{2} x^{1 / 2}+C\)
Answer:
(D) \(\frac{3}{2} x^{3 / 2}+\frac{1}{2} x^{1 / 2}+C\)
Explanation:
\(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right) d x=\int x^{1 / 2} d x+\int x^{-1 / 2} d x\)
\(=\frac{x^{3 / 2}}{\frac{3}{2}}+\frac{x^{1 / 2}}{\frac{1}{2}}+C\)
= \(\frac{2}{3} x^{3 / 2}+2 x^{1 / 2}+C\)
Question 23.
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}\) equals
(A) \(\frac {π}{3}\)
(B) \(\frac {2π}{3}\)
(C) \(\frac {π}{6}\)
(D) \(\frac {π}{12}\)
Answer:
(D) \(\frac {π}{12}\)
Explanation:
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}=F(\sqrt{3})-F(1)\)
= tan-1\(\sqrt{3}\) – tan-1 1
= \(\frac {π}{3}\) – \(\frac {π}{4}\)
= \(\frac {π}{12}\)
Question 24.
\(\int_{0}^{2 / 3} \frac{d x}{4+9 x^{2}}\) equals
(A) \(\frac {π}{6}\)
(B) \(\frac {π}{12}\)
(C) \(\frac {π}{24}\)
(D) \(\frac {π}{4}\)
Answer:
(C) \(\frac {π}{24}\)
Explanation:
\(\int \frac{d x}{4+9 x^{2}}=\int \frac{d x}{(2)^{2}+(3 x)^{2}}\)
Put 3x = t
⇒ 3dx = dt
∴ \(\int \frac{d x}{(2)^{2}+(3 x)^{2}}=\frac{1}{3} \int \frac{d t}{(2)^{2}+(t)^{2}}\)
= \(\frac{1}{3}\left[\frac{1}{2} \tan ^{-1} \frac{t}{2}\right]\)
= \(\frac{1}{6} \tan ^{-1}\left(\frac{3 x}{2}\right)\)
= F(x)
By second fundamental theorem of calculus, we obtain
\(\int_{0}^{2 / 3} \frac{d x}{4+9 x^{2}}=F\left(\frac{2}{3}\right)-F(0)\)
= \(\frac{1}{6} \tan ^{-1}\left[\frac{3}{2} \times \frac{2}{3}\right]-\frac{1}{6} \tan ^{-1}(0)\)
= \(\frac{1}{6} \tan ^{-1}(1)\)
= \(\frac{1}{6} \tan ^{-1}\left[\tan \frac{\pi}{4}\right]\)
= \(\frac{\pi}{24}\)
![]()
Question 25.
If \(\frac{d}{d x} f(x)=4 x^{3}-\frac{3}{x^{4}}\) such that f(2) = 0. Then f(x) is
(A) \(x^{4}+\frac{1}{x^{3}}-\frac{129}{8}\)
(B) \(x^{3}+\frac{1}{x^{4}}+\frac{129}{8}\)
(C) \(x^{4}+\frac{1}{x^{3}}+\frac{129}{8}\)
(D) \(x^{3}+\frac{1}{x^{4}}-\frac{129}{8}\)
Answer:
(C) \(x^{4}+\frac{1}{x^{3}}+\frac{129}{8}\)
Explanation:
It is given that,
\(\frac {d}{dx}\) f(x) = 4 x 3 – \(\frac{3}{x^{4}}\)
∴ Anti – derivauve of 4×3 – \(\frac{3}{x^{4}}\) = f(x)
∴ f(x) = \(\frac{3}{x^{4}}\)
f(x) = \(\frac{3}{x^{4}}\)
f(x) = \(\frac{3}{x^{4}}\)
f(x) = \(\frac{3}{x^{4}}\)
Also,
f(2) = 0
f(2) = (2)4 + \(\frac{1}{2^{3}}\) + C = 0
⇒ \(16+\frac{1}{8}+C\) = 0
⇒ C = –\(16+\frac{1}{8}\)
⇒ C = \(\frac{-129}{8}\)
∴ f(x) = \(x^{4}+\frac{1}{x^{3}}-\frac{129}{8}\)
Assertion And Reason Based MCQs (1 Mark each)
Directions¡In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as:
(A) Both A and R are true and R is the correct explanation of A
(B) Both A and R are true but R is NOT the correct explanation of A
(C) A is true but R is false
(D) A is false and R is True
Question 1.
Assertion (A): \(\int \frac{d x}{x^{2}+2 x+3}=\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{x+1}{\sqrt{2}}\right)+c\)
Reason (R): \(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
Answer:
(A) Both A and R are true and R is the correct explanation of A
Explanation:
\(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
This is a standard integral and hence R is true.
\(\int \frac{d x}{x^{2}+2 x+3}=\int \frac{d x}{(x+1)^{2}+(\sqrt{2})^{2}}\)
= \(\frac{1}{\sqrt{2}} \tan ^{-1}\left(\frac{x+1}{\sqrt{2}}\right)+c\)
Hence A is true and R is the correct explanation for A.
Question 2.
Assertion(A): \(\int e^{x}[\sin x-\cos x] d x=e^{x} \sin x+C\)
Reason (R): \(\int e^{x}\left[f(x)+f^{\prime}(x)\right] d x=e^{x} f(x)+c\)
Answer:
(D) A is false and R is True
Explanation:
\(\int e^{x}\left[f(x)+f^{\prime}(x)\right] d x\) = \(\int e^{x} f(x) d x+\int e^{x} f^{\prime}(x) d x\)
= \(f(x) e^{x}-\int f^{\prime}(x) e^{x} d x\) + \(+\int f^{\prime}(x) e^{x} d x\)
= \(e^{x} f(x)+c\)
Hence R is true.
\(\int e^{x}(\sin x-\cos x) d x\) = \(e^{x}(-\cos x)+c\)
= \(e^{x}(\cos x)+c\) [∵\(\frac{d}{d x}(-\cos x)=\sin x\)]
Hence A is false.
Question 3.
Assertion (A): \(\int x^{x}(1+\log x) d x=x^{x}+c\)
Reason (R): \(\frac{d}{d x}\left(x^{x}\right)=x^{x}(1+\log x)\)
Answer:
(A) Both A and R are true and R is the correct explanation of A
Explanation:
Let y = x3
log y = x log x
Differentiating w,r.t. x
\(\frac{1}{y} \frac{d y}{d x}=x\left(\frac{1}{x}\right)+\log x(1)\)
\(\frac{d y}{d x}=y(1+\log x)\)
= xx(1+log x)
Hence R is true.
Since \(\frac {d}{dx}\)(xx) = xx(1 + log x)
\(\int x^{x}(1+\log x) d x\) = xx + c
Using the concept of anti-derivative, A is true.
R is the correct explanation for A.
![]()
Question 4.
Assertion (A): \(\int x^{2} d x=\frac{x^{3}}{3}+c\)
Reason (R): \(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
Answer:
(C) A is true but R is false
Explanation:
Since
\(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
\(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
= \(\int e^{x^{2}} d x=e^{x^{3 / 3}}+c\)
∴ A is true.
\(\int e^{x^{2}}\) dx is a function
which can not be integrated.
∴ R is false.
Question 5.
Assertion (A): \(\int_{0}^{\pi / 2} \frac{\cos x}{\sin x+\cos x} d x=\frac{\pi}{4}\)
Reason (R): \(\int_{0}^{\pi / 2} \frac{\sin x}{\sin x+\cos x} d x=\frac{\pi}{4}\)
Answer:
(A) Both A and R are true and R is the correct explanation of A
Explanation:
Let I = \(\int_{0}^{\pi / 2} \frac{\sin x}{\sin x+\cos x} d x\) ………(i)
\(\int_{0}^{a} f(x) d x=\int_{0}^{a} f(a-x) d x\)
∴ \(I=\int_{0}^{\pi / 2} \frac{\sin \left(\frac{\pi}{2}-x\right) d x}{\sin \left(\frac{\pi}{2}-x\right)+\cos \left(\frac{\pi}{2}-x\right)}\)
I = \(\int \frac{\cos x}{\cos x+\sin x} d x\) ……….(ii)
Adding equations (i) + (ii),
2I = \(\int_{0}^{\pi / 2} \frac{\sin x+\cos x}{\sin x+\cos x} d x\)
= \(\int_{0}^{\pi / 2} 1 d x\)
= \([x]_{0}^{\pi / 2}\)
= \(\frac {π}{2}\)
I = \(\frac {π}{4}\)
Hence R is true.
From (ii), A is also true.
R is the correct explanation for A.
Question 6.
Assertion (A): \(\int_{-3}^{3}\left(x^{3}+5\right) d x=30\)
Reason (R): f(x) = x3 + 5 is an odd function
Answer:
(C) A is true but R is false
Explanation:
Let f(x) = x3 + 5
f(-x) = (-x)3 + 5
= -x3 + 5
f(x) is neither even nor odd. Hence R is false.
\(\int_{-3}^{3}\left(x^{3}+5\right) d x=30\) = 0 [∴x3 is odd]
\(\int_{-3}^{3} 5 d x=5[x]_{-3}^{3}=30\)
∴ \(\int_{-3}^{3}\left(x^{3}+5\right) d x=0+30=30\)
Hence A is true.
Question 7.
Assertion (A): \(\frac{d}{d x}\left[\int_{0}^{x^{2}} \frac{d t}{t^{2}+4}\right]=\frac{2 x}{x^{4}+4}\)
Reason (R): \(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
Answer:
(A) Both A and R are true and R is the correct explanation of A
Explanation:
\(\int \frac{d x}{x^{2}+a^{2}}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+c\)
: This is a standard integral and hence true.
So R is true.
\(\int_{0}^{x^{2}} \frac{d t}{t^{2}+4}=\left[\frac{1}{2} \tan ^{-1}\left(\frac{t}{2}\right)\right]_{0}^{x^{2}}\)
= \(\frac{1}{2} \tan ^{-1}\left(\frac{x^{2}}{2}\right)\)
\(\frac{d}{d x}\left[\int_{0}^{x^{2}} \frac{d t}{t^{2}+4}\right]=\frac{d}{d x}\left[\frac{1}{2} \tan ^{-1}\left(\frac{x^{2}}{2}\right)\right]\)
= \(\frac{1}{2} \times \frac{1}{1+\frac{x^{4}}{4}} \times \frac{2 x}{2}\)
= \(\frac{x}{2} \times \frac{4}{4+x^{4}}\)
= \(\frac{2 x}{4+x^{4}}\)
Hence A is true and R is the correct explanation for A.
![]()
Question 8.
Assertion (A): \(\int_{-1}^{1}\left(x^{3}+\sin x+2\right) d x\) = 0
Reason (R):
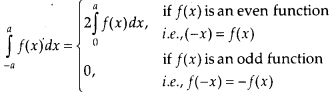
Answer:
(D) A is false and R is True
Explanation:
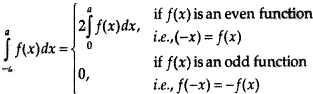
This is a property of the definite integrals and hence R is true.
\(\int_{-1}^{1}\left(x^{3}+\sin x+2\right) d x\) = 0
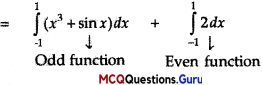
= \(0+2[x]_{-1}^{1}\)
= 2 x 2
= 4
Hence A is false.
Case-Based MCQs
Attempt any four sub-parts from each question.
Each sub-part carries 1 mark.
I. Read the following text and answer the following questions on the basis of the same:
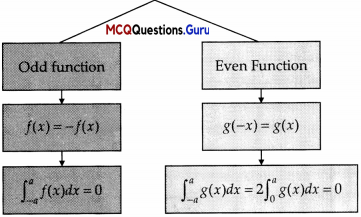
Question 1.
\(\int_{-1}^{1} x^{99}\) dx = …………….
(A) 0
(B) 1
(C) -1
(D) 2
Answer:
(A) 0
Explanation:
\(\int_{-1}^{1} x^{99}\) dx = 0, since x99 is an odd function.
Question 2.
\(\int_{-\pi}^{\pi} x \cos x d x\) = …………..
(A) 1
(B) 0
(C) -1
(D) \(\frac {π}{2}\)
Answer:
(B) 0
Explanation:
\(\int_{-\pi}^{\pi} x \cos x d x\) = 0, since x cos x is an odd function.
Question 3.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{3} x d x\) = …………..
(A) 1
(B) 0
(C) -1
(D) π
Answer:
(B) 0
Explanation:
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{3} x d x\) = 0, since sin3x dx = 0 is an odd function.
![]()
Question 4.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^{3} x d x\) = …………..
(A) π
(B) 0
(C) 2π
(D) \(\frac {π}{2}\)
Answer:
(C) 2π
Explanation:
Since x sin x is an even function
\(\int_{-\pi}^{\pi} x \sin x d x\) = \(2 \int_{0}^{\pi} x \sin x d x\)
= 2 \(2\left[-x \cos x+\int(1 \times \cos x d x)\right]_{0}^{\pi}\)
= 2 \(2[-x \cos x+\sin x]_{0}^{\pi}\)
= 2[(π + 0) – (0 + 0)]
= 2π
Question 5.
\(\int_{-\pi}^{\pi} \tan x \sec ^{2} x d x\) = …………..
(A) 1
(B) -1
(C) 0
(D) 2
Answer:
(C) 0
Explanation:
\(\int_{-\pi}^{\pi} \tan x \sec ^{2} x d x\) = 0, Sìnce it is an odd function
II. Read the following text and answer the following questions on the basis of the same:
\(\int e^{x}\left[f(x)+f^{\prime}(x)\right] d x\) = \(\int e^{x} f(x) d x+\int e^{x} f^{\prime}(x) d x\)
= \(f(x) e^{x}-\int f^{\prime}(x) e^{x} d x\) + \(\int f^{\prime}(x) e^{x} d x\)
= \(e^{x} f(x)+c\)
Question 1.
\(\int e^{x}(\sin x+\cos x) d x\) = …………..
(A) ex cos x + C
(B) ex sin x + C
(C) ex + C
(D) ex(-cos x + sin x) + c
Answer:
(B) ex sin x + C
Explanation:
\(\int e^{x}(\underbrace{\sin x}_{f(x)}+\underbrace{\cos x}_{f^{\prime}(x)}) d x=e^{x} \sin x+c\)
Question 2.
\(\int e^{x}\left(\frac{x-1}{x^{2}}\right) d x\) dx = …………..
(A) ex + C
(B) \(\frac{e^{x}}{x}+c\)
(C) \(\frac{e^{x}}{x^{2}}+c\)
(D) \(\frac{-e^{x}}{x^{2}}+c\)
Answer:
(B) \(\frac{e^{x}}{x}+c\)
Explanation:
\(\int e^{x}\left(\frac{x-1}{x^{2}}\right) d x\) = \(\int e^{x}\left(\frac{\frac{1}{x}}{\frac{x}{f(x)}}-\frac{\frac{1}{x^{2}}}{f^{\prime}(x)}\right) d x\)
= \(\frac{e^{x}}{x}+c\)
Question 3.
\(\int e^{x}(x+1) d x\) = …………….
(A) x ex + C
(B) ex + C
(C) ex + C
(D) None of these
Answer:
(A) x ex + C
Explanation:
\(\int e^{x}\left(\underset{f(x)}{x}+\underset{f^{\prime}(x)}{1}\right) d x=x e^{x}+c\)
Question 4.
\(\int_{0}^{\pi} e^{x}\left(\tan x+\sec ^{2} x\right) d x\) = …………..
(A) 0
(B) 1
(C) -1
(D) -ex
Answer:
(A) 0
Explanation:
\(\int_{0}^{\pi} e^{x}\left(\tan x+\sec ^{2} x\right) d x=\left[e^{x} \tan x\right]_{0}^{\pi}=0\)
![]()
Question 5.
\(\int \frac{x e^{x}}{(1+x)^{2}}\) = …………..
(A) \(x e^{x}+c\)
(B) \(\frac{e^{x}}{(x+1)^{2}}+c\)
(C) \(\frac{x e^{x}}{x+1}+c\)
(D) \(\frac{e^{x}}{x+1}+c\)
Answer:
(D) \(\frac{e^{x}}{x+1}+c\)
Explanation:
\(\int e^{x}\left[\frac{(x+1)-1}{(x+1)^{2}}\right] d x\) = \(\int e^{x}\left[\frac{1}{x+1}-\frac{1}{(x+1)^{2}}\right] d x\)
= \(\frac{e^{x}}{x+1}+c\)
III. Read the following text and answer the following questions on the basis of the same:
Let’s say that we want to evaluate \(\int[P(x) / Q(x)]\) where P(x) is a proper rational fraction. In such cases, it is possible to write the integrand as a sum of simpler rational functions by using partial fraction decomposition. Post this, integration can be carried out easily. The following image indicates some simple partial fractions which can be associated with various rational functions:

In the above table, A, B and C are real numbers to be determined suitably.
Question 1.
\(\frac{e^{x}}{x+1}+c\)
(A) log\(\frac{e^{x}}{x+1}+c\) + C
(B) 1og\(\frac{e^{x}}{x+1}+c\) + C
(C) log\(\frac{e^{x}}{x+1}+c\) + C
(D) log\(\frac{e^{x}}{x+1}+c\) + C
Answer:
(A) log\(\frac{e^{x}}{x+1}+c\) + C
Explanation:
We write,
\(\frac{1}{(x+1)(x+2)}\) = \(\frac{A}{x+1}+\frac{B}{x+2}\) ………(i)
where; real number A and B are to be determined suitably. This gives
1 = A(x + 2) + B(x + 1)
Equating the coefficients of x and the constant term, we get
A + B = 0 and 2A + B = 1
Solving these equatlons,we get A = 1 and B = -1.
Thus, the Integrand Is given by
\(\frac{1}{(x+1)(x+2)}\) = \(\frac{1}{x+1}+\frac{-1}{x+2}\)
Therefore,
\(\int \frac{d x}{(x+1)(x+2)}=\int \frac{d x}{x+1}-\int \frac{d x}{x+2}\)
= \(\log |x+1|-\log |x+2|+C\)
= \(\log \left|\frac{x+1}{x+2}\right|+C\)
![]()
Question 2.
Integration of (x + 1)(x +2)
(A) log \(\frac{(x+1)^{2}}{(x+2)}\) + C
(B) log \(\frac{(x+2)^{2}}{(x+1)}\) + C
(C) log \(\frac{(x)^{2}}{(x+1)}\) + C
(D) log \(\frac{(x-2)^{2}}{(x+1)}\) + C
Answer:
(B) log \(\frac{(x+2)^{2}}{(x+1)}\) + C
Explanation:
Let
\(\frac{x}{(x+1)(x+2)}=\frac{A}{(x+1)}+\frac{B}{(x+2)}\)
⇒ x = A(x + 2) + B(x + 1)
Equating the coefficients of x and constant term, we obtain
A + B = 1
2A + B = 0
On solving, we obtain
A = -1 and B = 2
\(\frac{x}{(x+1)(x+2)}=\frac{-1}{(x+1)}+\frac{2}{(x+2)}\)
⇒ \(\int \frac{x}{(x+1)(x+2)} d x=\int \frac{-1}{(x+1)}+\frac{2}{(x+2)} d x\)
= – log |x + 1| + 2 log |x + 2| + C
= log(x + 2)2 – 1og |x + 1|+ C
= log \(\frac{(x+2)^{2}}{(x+1)}\) + C
Question 3.
\(\int \frac{1}{x^{2}-9}\)dx
(A) \(\frac{1}{6} \log \left|\frac{x-3}{x+3}\right|+C\)
(B) \(\frac{1}{6} \log \left|\frac{x-2}{x+3}\right|+C\)
(C) \(\frac{1}{6} \log \left|\frac{x+3}{x-3}\right|+C\)
(D) \(\frac{1}{3} \log \left|\frac{x-3}{x+3}\right|+C\)
Answer:
(A) \(\frac{1}{6} \log \left|\frac{x-3}{x+3}\right|+C\)
Explanation:
Let
\(\frac{1}{(x+3)(x-3)}=\frac{A}{(x+3)}+\frac{B}{(x-3)}\)
I = A(x – 3)+B(x + 3)
Equating the coefficients of x and constant term, we obtain
A + B = 0
-3A + 3B = 1
On solving, we obtain
A = –\(\frac{1}{6}\) and B = \(\frac{1}{6}\)
∴ \(\frac{1}{(x+3)(x-3)}=\frac{-1}{6(x+3)}+\frac{1}{6(x-3)}\)
⇒ \(\int \frac{1}{\left(x^{2}-9\right)} d x=\int\left(\frac{-1}{6(x+3)}+\frac{1}{6(x-3)}\right) d x\)
= \(-\frac{1}{6} \log |x+3|+\frac{1}{6} \log |x-3|\) + C
= \(\frac{1}{6} \log \left|\frac{(x-3)}{(x+3)}\right|+C\)
Question 4.
\(\int \frac{1}{e^{x}-1} d x\)
(A) 1og\(\left|\frac{e^{x}-1}{2}\right|\) + C
(B) 1og\(\left|\frac{e^{x}-1}{2 e^{x}}\right|\) + C
(C) log\(\left|\frac{e^{x}-1}{2 x}\right|\) + C
(D) log\(\left|\frac{e^{x}-1}{e^{x}}\right|\) + C
Answer:
(D) log\(\left|\frac{e^{x}-1}{e^{x}}\right|\) + C
Explanation:
Let
ex = t
⇒ ex dx = dt
⇒ \(\int \frac{1}{e^{x}-1} d x=\int \frac{1}{t-1} \times \frac{d t}{t}\)
= \(\int \frac{1}{t(t-1)} d t\)
Let \(\frac{1}{t(t-1)}=\frac{A}{t}+\frac{B}{t-1}\)
1 = A(t – 1) + Bt ………..(i)
Substituting t = 1 and t = O in equation (i), we obtain
A = -1 and B = 1
∴\(\frac{1}{t(t-1)}=\frac{-1}{t}+\frac{1}{t-1}\)
⇒ \(\int \frac{1}{t(t-1)} d t=\log \left|\frac{t-1}{t}\right|+C\)
= \(\log \left|\frac{e^{x}-1}{e^{x}}\right|+C\)
![]()
Question 5.
\(\int \frac{d x}{x\left(x^{2}+1\right)}\) =
(A) \(\log |x|+\frac{1}{2} \log \left|x^{2}+1\right|+C\)
(B) \(\log |x|-\frac{1}{4} \log \left|x^{2}+1\right|+C\)
(C) \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|+C\)
(D) \(\log |x|-\frac{1}{3} \log \left|x^{2}-1\right|+C\)
Answer:
(C) \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|+C\)
Explanation:
Let
\(\frac{1}{x\left(x^{2}+1\right)}=\frac{A}{x}+\frac{B x+C}{x^{2}+1}\)
1 = A(x2 + 1) + (Bx + C)x
Equating the coefficients of x2, x and constant
term, we obtain
A + B = 0
C = 0
A = 1
On solving these equations, we obtain
A =1, B = -1, and C = 0
∴ \(\frac{1}{x\left(x^{2}+1\right)}=\frac{1}{x}+\frac{-x}{x^{2}+1}\)
⇒ \(\int \frac{1}{x\left(x^{2}+1\right)} d x=\int\left\{\frac{1}{x}-\frac{x}{x^{2}+1}\right\} d x\)
= \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|+C\)