MCQ Questions for Class 12 Maths Chapter 6 Application of Derivatives

Application of Derivatives Class 12 MCQs Questions with Answers

Application Of Derivatives Class 12 MCQ Question 1.
A ladder, 5 metre long, standing on a horizontal floor, leans against a vertical wall. ¡f the top of the ladder slides downwards at the rate of 10 cm/sec.
then the rate at which the angle between the (loor and the ladder is decreasing when lower end of ladder is 2 metre from the wall is:
(A) \(\frac {1}{10}\) radian/sec
(B) \(\frac {1}{20}\) radian/sec
(C) 20 radianìsec
(D) 10 radian/sec
Answer:
(B) \(\frac {1}{20}\) radian/sec

Explanation:
Let the angle between floor and the ladder be θ.
Let AB = x an and BC = y cm

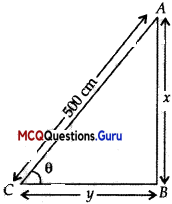
sin θ = \(\frac{x}{500}\) and cos θ = \(\frac{y}{500}\)
⇒ x = 500 sin θ and y = 500 cos θ
Also, \(\frac{dθ}{dt}\) = 10 cm/s
= 500.cos θ \(\frac{dx}{dt}\) = 10 cm/s
⇒ \(\frac{d \theta}{d t}=\frac{10}{500 \cos \theta}=\frac{1}{50 \cos \theta}\)
For y = 2 m = 200cm,
\(\frac{dθ}{dt}\) = \(\frac{1}{50 \cdot \frac{y}{500}}\)
= \(\frac{10}{y}\)
= \(\frac{10}{200}\)
= \(\frac{1}{20}\) rad/s

Application Of Derivatives MCQ Chapter 6 Question 2.
For the curve y = 5x² – 2x³, if r increases at the rate of 2 units/sec. then at x = 3 the slope of curve is changing at ……………… units/sec.
(A) -72
(8) -36
(C) 24
(D) 48
Answer:
(A) -72

Explanation:
Given
curve is y = 5x – 2x³
or \(\frac{dy}{dx}\) = 5 – 6x²
or m = 5 – 6x² [slope m = \(\frac{dy}{dx}\)]
\(\frac{dm}{dt}\) = -12x \(\frac{dx}{dt}\) = -24x
\(\left.\frac{d m}{d t}\right|_{x=3}\) = -72

Class 12 Maths Chapter 6 MCQ Questions Question 3.
The contentment obtained after eating x units of a new dish at a trial function is given by the function fix) = x³ + 6x² + 5x + 3. The marginal contentment when 3 units of dish are consumed is …………..
(A) 60
(B) 68
(C) 24
(D) 48
Answer:
(B) 68

Exp1anation.
f(x) = x³ + 6x² + 5x + 3
\(\frac{d f(x)}{d x}\) = 3x² + 12x + 5
At x = 3, ,
Marginal contentment
= 3 x (3)² +12 x 3 + 5
= 27 + 36 + 5
= 68 units.

MCQ On Application Of Derivatives Class 12 Question 4.
A particle moves along the curve x² = 2y. The point at which, ordinate increases at the same rate as the abscissa is …………
(A) (1,2)
(B) (\(\frac{1}{2}\),1)
(C) (\(\frac{1}{2}\),\(\frac{1}{2}\))
(D) (1,\(\frac{1}{2}\))
Answer:
(B) (\(\frac{1}{2}\),1)

Explanation:
x² = 2y ……….(1)
⇒2x\(\frac{dx}{dt}\) = 2\(\frac{dy}{dt}\) (given \(\frac{dy}{dt}\) = \(\frac{dx}{dt}\))
2x\(\frac{dx}{dt}\) = 2\(\frac{dx}{dt}\)
⇒ x = 1
From (1) y = \(\frac{1}{2}\)
so point is (1,\(\frac{1}{2}\))

Application Of Derivatives Class 12 MCQ Questions Question 5.
The curve y = \(x^{1 / 5}\) has at (0, 0)
(A) a vertical tangent (parallel lo y.axis)
(B) a horizontal tangent (parallel to x-axis)
(C) an oblique tangent
(D) no tangent
Answer:
(A) a vertical tangent (parallel lo y.axis)

Explanation:
Given that, y = x\(x^{1 / 5}\)
On differentiating with respect to x, we get
\(\frac{dx}{dt}\) = \(\frac{1}{5}\)x\(x^{1 / 5}\) = \(\frac{1}{5}\)\(x^{-4 / 5}\)
∴ \(\frac{dx}{dt}\)_(0,0) = \(\frac{1}{5}\) x (0)\(x^{-4 / 5}\) = ∞
So, the curve y = \(x^{1 / 5}\) has a vertical tangent at (0, 0), which is parallel to y-axis.

MCQ Of Application Of Derivatives Class 12 Chapter 6 Question 6.
The equation of normal to the curve 3x² – y² = 8 which is parallel to the line x + 3y = 8 is
(A) 3x – y = 8
(A) 3x + y + 8 = 0
(C) x + 3y ± 8 = 0
(D) x + 3y = 0
Answer:
(C) x + 3y ± 8 = 0

Explanation :
We have, the equation of the curve 1s 3 x 1 – y² = 8
Also, the given equation of the line is x + 3y = 8.
⇒ 3y = 8 – x
⇒ y = – \(\frac{x}{3}\) + \(\frac{8}{3}\)
Thus, slope of the line is – \(\frac{1}{3}\) which should be equal to slope of the equation of normal to the curve. On differentiating equation (1) with respect to x,
we get
6x – 2y = 0

⇒ \(\frac{d y}{d x}=\frac{6 x}{2 y}=\frac{3 x}{y}\) = Slope of the curve
Now, slope of normal to the curve
= \(-\frac{1}{\left(\frac{d y}{d x}\right)}\)
= \(\frac{1}{\left(\frac{3 x}{y}\right)}\)
= – \(\frac{y}{3x}\)
∴ \(-\left(\frac{y}{3 x}\right)=-\frac{1}{3}\)
= -3y = -3x
= y = x
On substituting the value of the given equation of the curve, we get
3x² – x² = 8
2x² = 8
x² = 4
⇒ x ± 2
For x = 2
3(2)² – y² = 8
⇒ y² = 4
⇒ y² = ± 2
and for x = -2
3 (2)² – y² = 8
⇒ y² = 4
y = ±2
So, the points at which normal is parallel to the
given line are (±2, ±2).
Hence, the equation of normal at (±2, ±2) is
= y – (±2) = \(\frac{1}{3}\)[x – (±2)]
= 3[(y – (±2)] = -[(x-(±2)]
∴ x + 3y ± 8 = 0

Class 12 Maths Chapter 6 MCQ Question 7.
If the curve ay + x² =7 and x³ = y. cut orthogonally at (1, 1), then the value of a is:
(A) 1
(B) 0
(C) – 6
(D) 6
Answer:
(D) 6

Explanation :
Given that, ay + x² = 7 and x² = y on differentiating both equations with respect to x we get
a \(\frac{dy}{dx}\) + 2x = 0 and 3x² = \(\frac{dy}{dx}\)
⇒ \(\frac{dy}{dx}\) = –\(\frac{2x}{a}\) and \(\frac{dy}{dx}\) = 3x²
\(\frac{dy}{dx}\) = \(\frac{-2}{a}\) = m₂
Since, the curve cuts orthogonally at (1, 1).
∴ m₁ m₂ = -1
⇒ \(\frac{-2}{a}\).3 = -1
∴ a = 6

Applications Of Derivatives Class 12 MCQ Chapter 6 Question 8.
The equation of tangent to the curve
y(1 + x²) = 2 – x, where it crosses x-axis is:
(A) x + 5y = 2
(B) x – 5y = 2
(C) 5x – y = 2
(D) 5x + y = 2
Answer:
(A) x + 5y = 2

Explanation:
Given that the equation of curve is
y(1 + x³) = 2 – x ……….(i)
On differentiating with respect to x, we get
∴ y.(0 + 2x) + (1 + x²) \(\frac{dy}{dx}\) = 0 – 1

⇒ 2xy + (1 + x²) = -1
\(\frac{dy}{dx}\) = \(\frac{-1-2 x y}{1+x^{2}}\) ……….(ii)
Since, the given curve passes through x-axis,
i.e., y = 0
0(1 + x²) = 2 – x [By using EQuestion (i)]
⇒ x = 2
So the curve passes through the point (2,0).
∴ \(\frac{dy}{dx}\)_(2,0) = \(\frac{-1-2 \times 0}{1+2^{2}}\) = –\(\frac{1}{5}\) = Slope of the curve
∴ Slope of tangent to the curve = –\(\frac{1}{5}\)
∴ Equation of tangent to the curve passing through (2,0) is

MCQ On Derivatives Class 12 Chapter 6 Question 9.
The points at which the tangents to the curve y = x³ – 12x + 18 are parallel to x – axis are:
(A) (2, -2), (-2, -34)
(B) (0,34), (-2,0)
(C) (2, 34), (-2,0)
(D) (2, 2), (-2,34)
Answer:
(D) (2, 2), (-2,34)

Explanation :
The equation of the curve is given by
y = x³ – 12x + 18
On differentiating with respect to x, we get
∴ \(\frac{dy}{dx}\) = 3x² – 12
So, the slope of line parallel to the x-axis,
\(\frac{dy}{dx}\) = 0
⇒ 3x³ – 12 = 0
⇒ x² = \(\frac{12}{3}\)
⇒ x² = 4
∴ x = ±2
For x = 2,
y = 2³ – 12x² + 18 = 2
and for x = -2,
y = (-2) -12x(-2) + 18 = 34
So, the points are (2,2) and (-2, 34).

MCQ On Application Of Derivatives Chapter 6 Question 10.
The tangent to the curve y = e^2x at the point (0, 1) meets x-axis at:
(A) (0,1)
(B) (- \(\frac{1}{2}\),o)
(C) (2,0)
(D) (0,2)
Answer:
(B) (- \(\frac{1}{2}\),o)

Explanation :
The equation of the curve is given by y = e^2x
Since, it passes through the point (0,1).
∴ \(\frac{dy}{dx}\) = e^2x.2
= 2 e^2x
\(\frac{dy}{dx}\)_(0,1) = 2e^2.0 = 2
= Slope of tangent to the curve.
∴ Equation of tangent is
y – 1 = 2(x – 0)
y = 2x + 1
Since, tangent to the curve y = e^2x at the point
(0, 1) meets x-axis, i.e. y = 0.
∴ 0 = 2x + 1
x = – \(\frac{1}{2}\)
so the required Point is (- \(\frac{1}{2}\), o).

Class 12 Application Of Derivatives MCQ Chapter 6 Question 11.
The interval on which the function f(x) = 2x³ + 9x² + 12x – 1 is decreasing is:
(A) [-1, ∞]
(B) [-2, -1]
(C) (- ∞,-2]
(D) (-1, 1]
Answer:
(B) [-2, -1]

Explanation:
Given that,
f(x) = 2x³ + 9x² + 12x -1
f(x) = 6x³ + 18x + 12
= 6(x² + 3x + 2)
= 6(x + 2)(x + 1)
So, f ‘(x) ≤ 0,for decreasing.
On drawing number lines as below:

We see that f’(x) is decreasing in[-2,-1].

Question 12.
y = x(x – 3)² decreases for the values of x given by:
(A) 1 < x < 3
(B) x < 0 (C) x > 0
(D) 0 < x < \(\frac {3}{2}\)
Answer:
(A) 1 < x < 3

Explanation:
Given that,
y = x(x – 3)²
∴ \(\frac{dy}{dx}\) = x.2 (x – 3).1 + (x – 3)².1
= 2x² – 6x + x² + 9 – 6x
= 3x² – 12x + 9
= 3(x² – 3x – x + 3)
= 3(x – 3)(x – 1)
So, y = x(x – 3)² decreases for(1,3).
[Since, y’ < 0 for all x ∈ (1, 3), hence y is decreasing on (1,3)].

MCQ Questions On Application Of Derivatives Chapter 6 Question 13.
The function f(x) = 4 sin³x – 6 sin²x + 12 sin x + 100 is strictly
(A) increasing in (π, \(\frac{3π}{2}\))
(B) decreasing in (\(\frac{3π}{2}\), π)
(C) decreasing in (\(\frac{-π}{2}\),\(\frac{π}{2}\))
(D) decreasing in (0, \(\frac{π}{2}\))
Answer:
(B) decreasing in (\(\frac{3π}{2}\), π)

Explanation:
Given that,
f(x) = 4 sin³ x – 6 sin²x + 12 sin x + 100
On differentiating with respect to x, we get
f'(x) = 12 sin² x. cos x – 12 sin x. cos x + 12 cos x
= 12[sin²x.cos x – sin x.cos x + cos x ]
= 12 cos x[sin² x – sin x + 1]
⇒ f'(x) = 12 cos x[sin² x + 1(1 – sin x)]
⇒ 1 – sin x ≥ 0 and sin² x ≥ 0
⇒ sin² x + 1 – sin x ≥ 0

Hence, f'(x) > 0, when cos x >0, i.e, x ∈\(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
So.f(x) is increasing when x ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
and f (x) < 0, when cos x < 0, i.e., x ∈\(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)
Hence, f’ (x) is decreasing when x ∈\(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)
Since \(\left(\frac{\pi}{2}, \pi\right)\)∈\(\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\)
Hence,f(x) is decreasing in\(\left(\frac{\pi}{2}, \pi\right)\)

Derivatives MCQ Questions Chapter 6 Question 14.
Which of the following functions is decreasing on \(\left(0, \frac{\pi}{2}\right)\)
(A) sin 2x
(B) tan x
(C) cos x
(D) cos3x
Answer:
(C) cos x

Explanation:
In the given interval \(\left(0, \frac{\pi}{2}\right)\)
f(x) = cos x
On differentiating with respect to x, we get
f’(x) = – sin x
which gives f’(x) < 0 in (\(\left(0, \frac{\pi}{2}\right)\)) Hence, f(x) = cos x is decreasing in (o, \(\left(0, \frac{\pi}{2}\right)\)).

MCQ Application Of Derivatives Chapter 6 Question 15.
The function f(x) = tan x – x
(A) always increases
(B) always decreases
(C) never increases
(D) sometimes increases and sometimes decreases
Answer:
(A) always increases

Explanation: We have, f(x) = tan x – x On differentiating with respect to x, we get f'(x) = sec x – 1 f'(x) > 0,∀ x ∈R
So, f(x) always increases.

Class 12 Maths Ch 6 MCQ Question 16.
Let the f : R →R be defined by f(x) = 2x + cos x then f:
(A) has a minimum at x = π
(B) has a maximum, at x = 0
(C) is a decreasing function
(D) is an increasing function
Answer:
(D) is an increasing function

Explanation:
Given that,
f(x) = 2x + cos x
Differentiating with respect to x, we get
f'(x) = 2 + (-sin x)
= 2 – sin x
Since, f(x) > 0, ∀ x ∈ R
Hence, f(x) is an increasing function.

MCQs On Application Of Derivatives Chapter 6 Question 17.
If x is real, the minimum value of x² – 8x + 17 is
(A) -1
(B) 0
(C) 1
(D) 2
Answer:
(C) 1

Explanation:
Let,
f(x) = x² – 8x + 17
On differentiating with respect to x, we get
f’(x) = 2x – 8
So, f'(x) = 0
2x – 8 = 0
So, f’(x) = 0
2x – 8 = 0
2x = 8
∴ x = 4
Now, Again on differentiating with respect to x,
we get
f'(x) = 2 > 0,∀x
So,x = 4 is the point of local minimum.
Minimum value of f(x) at x = 4
f(4) = 44 – 84 + 17 = 1

Ch 6 Maths Class 12 MCQ Question 18.
The smallest value of the polynomial x³ – 18 x² + 96x in [0, 9] is
(A) 126
(B) 0
(C) 135
(D) 160
Answer:
(B) 0

Explanation:
Given that, the smallest value of
polynomial is f(x) = x³ – 8x² + 96x
On differentiating with respect to x we get
f'(x) = 3x² – 36 x + 96
So,
f’(x) = 0
3x² – 36x + 96 = 0
= 3(x² – 12x + 32) = 0
(x – 8)(x – 4) = 0
x = 8,4 ∈[0,9]
We shall now calculate the value of f(x) at these points and at the end points of the interval [0, 9]
Le., at x = 4 and x = 8 and at x = 0 and at x = 9.
f(4) = 4³ – 18 × 4² + 96 × 4
= 64 – 288 + 384 = 160
f(8) = 8³ – 18 × 8² + 96 × 8 = 128
f(9) = 9³ -18 × 9² + 96 × 9
=729 – 1458 + 864 = 135
and f(0) = 0³ – 18 x 0² +96 x 0 = 0
Thus, we conclude that absolute minimum value of fix) in 10,91 is 0 occurring at x 0.

MCQ Of Derivatives Class 12 Chapter 6 Question 19.
The function f(x) = 2x³ – 3x² – 12x + 4, has
(A) two points of local maximum
(B) two points of local maxiuma
(C) one maxium and one minimum
(D) no maxima or minima
Answer:
(C) one maxium and one minimum

Explanation:
We have,
f(x) = 2x³ – 3x² – 12x + 4
f'(x) = 6x² – 6x – 12
Now, f'(x) = 0
⇒ 6(x² – x – 2) = 0
6(x + 1)(x – 2) = 0
x = -1 and x = +2
On number line for f(x), we get

Hence, x= -1 is point of local maxima and x = 2 is point of local minima.
So,f(x) has one maxima and one minima.

MCQ Of Chapter 6 Maths Class 12 Question 20.
The maximum value of sin x. cos x is
(A) \(\frac {1}{4}\)
(B) \(\frac {1}{2}\)
(C) \(\sqrt{2}\)
(D) \(2 \sqrt{2}\)
Answer:
(B) \(\frac {1}{2}\)

Explanation:
Let us assume that,
f(x)= sin x.cos x
Now, we know that
sin x. cos x = \(\frac {1}{2}\) sin2x
∴ f'(x) = \(\frac {1}{2}\) cos 2x. 2 = cos2x
Now, f'(x) = 0
⇒ cos 2x = 0
⇒ cos 2x = cos \(\frac {π}{2}\)
x = \(\frac {π}{4}\)
Also f”(x) = \(\frac {d}{dx}\).cos 2x = -2 sin 2x
∴ \(\left[f^{\prime \prime}(x)\right]_{\text {at } x=\frac{\pi}{4}}\) = -2 sin 2. \(\frac {π}{4}\)
= – 2 sin \(\frac {π}{2}\)
= – 2<0
∴ x \(\frac {π}{4}\) is point of maxiuma.
f(\(\frac {π}{4}\)) = \(\frac {1}{2}\).sin.2\(\frac {π}{4}\)
= \(\frac {1}{2}\)

Question 21.
Maximum slope of the cwve y = -x³ + 3x² + 9x -27 is:
(A) 0
(B) 12
(C) 16
(D) 32
Answer:
(B) 12

Explanation:
Given that,
y = -x³ + 3x² + 9x – 27
∴\(\frac {dy}{dx}\) = -3x² + 6x + 9
= Slope of the curve
and \(\frac{d^{2} y}{d x^{2}}\) = -6x + 6 = -6(x – 1)
∴\(\frac{d^{2} y}{d x^{2}}\) = -6x + 6 = -6(x – 1)
∴\(\frac{d^{2} y}{d x^{2}}\) = 0
⇒ -6(x – 1) = 0
x = 1 > 0
Now, \(\frac{d^{2} y}{d x^{2}}\) = -6 < 0
So, the maximum slope of given curve is at x = 1.
∴\(\left(\frac{d y}{d x}\right)_{(x=1)}\) = -3 x 1² +6 x 1 + 9 = 12

Question 22.
The maximum value of \(\left(\frac{1}{x}\right)^{x}\) is:
(A) e
(B) e ^x
(C) \(e^{1 / e}\)
(D) \(\left(\frac{1}{e}\right)^{1 / e}\)
Answer:
(C) \(e^{1 / e}\)

Explanation:
Let y = \(\left(\frac{1}{x}\right)^{x}\)
log y = x. log \(\frac{1}{x}\)
∴ \(\frac{1}{y} \cdot \frac{d y}{d x}\) = \(x \cdot \frac{1}{\frac{1}{x}} \cdot\left(-\frac{1}{x^{2}}\right)+\log \frac{1}{x}, 1\)
= -1 + log \(\frac{1}{x}\)
∴ \(\frac{d y}{d x}=\left(\log \frac{1}{x}-1\right) \cdot\left(\frac{1}{x}\right)^{x}\)
Now, \(\frac{dy}{dx}\) = 0
⇒ log \(\frac{1}{x}\) = 1 = loge
⇒ \(\frac{1}{x}\) = e
⇒ x = \(\frac{1}{e}\)
Hence, the maximum value of f = \(\frac{1}{e}\) = \((e)^{1 / e}\)

Assertion And Reason Based Mcqs (1 Mark Each)

Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R) Mark the correct choice as.
(A) Both A and R are true and R is the correct explanation of A
(B) Both A and R are true but R is NOT the correct explanation of A
(C) A is true but R is false
(D) A is false and R is True

Question 1.
The total revenue received from the sale of x units of a product is given by R(x) = 3x² + 36x + 5 in rupees.
Assertion (A): The marginal revenue when x = 5 is 66.
Reason (R): Marginal revenue is the rate of change of total revenue with respect to the number of items sold at an instance.
Answer:
(A) Both A and R are true and R is the correct explanation of A

Marginal revenue is the rate of change of total revenue with respect to the number of items sold at an instance. Therefore R is true.
R'(x) = 6x +36
R'(5) = 66
∴ A is true.
R is the correct explanation of A.

Question 2.
The radius r of a right circular cylinder is increasing at the rate of 5 cm/mm and its height h, is decreasing at the rate of 4 cm/min.
Assertion (A): When r = 8cm and h = 6 cm, the rate of change of volume of the cylinder is 224 π cm³/min
Reason (R): The volume of a cylinder is V =\(\frac {1}{3}\) πr²h
Answer:
(C) A is true but R is false

Explanation:
The volume of a cylinder is V = πr²h
So R is false.
\(\frac {dr}{dt}\) = 5cm/min, \(\frac {dh}{dt}\) = -4 cm/min
V = πr²h
\(\frac {dV}{dt}\) = π\(\left(r^{2} \frac{d h}{d t}+2 h r \frac{d r}{d t}\right)\)
\(\frac {dV}{dt}\) = π[64 × (-4) + 2 × 6 × 8 × 5]
\(\left.\frac{d V}{d t}\right)_{r=8, h=6}\) = 224 π cm³ /mm
∴ Volume is increasing at the rate of 224 π cm³ /mm
∴ A is true.

Question 3.
Assertion (A): For the curve y = 5x – 2x³ if x increases at the rate of 2 units/sec, then at x = 3 the slope of curve is decreasing at 36 units/sec.
Reason (R): The slope of the curve is
Answer:
(D) A is false and R is True

Explanation:
The slope of the curve y = f(x) is \(\frac {dy}{dt}\)
R is true.
Given curve is y = 5x – 2x³
or \(\frac {dy}{dt}\) = 5 – 6x²
or m = 5 – 6x² [slope m = \(\frac {dy}{dx}\)]
\(\frac {dm}{dt}\) = -12x \(\frac {dx}{dt}\) = -24x [∴ \(\frac {dx}{dt}\) = 2 unit/sec]
\(\left.\frac{d m}{d t}\right|_{x=3}=-72\)

Rate of Change of the slope is decreasing by 72 units/s
A is false.

Question 4.
A particle moves along the curve 6y = x² + 2.
Assertion (A): The curve meets the Y axis at three points.
Reason (R): At the points (2 ) and (-2, -1) the ordinate changes two times as fast as the abscissa.
Answer:
(D) A is false and R is True

Explanation:
On Y axis, x = 0. The curve meets the Y axis at
only one point, i.e., (o,\(\frac{1}{3},\) ).
Hence A is false.
6y = x³ + 2
or 6\(\frac{d y}{d t}\) = 3x²\(\frac{dx}{d t}\)
Given, \(\frac{d y}{d t}\) = 2 \(\frac{dx}{d t}\)
or 12 = 3x²
or x = ±2
Put x = 2 and -2 in the given equation to get y
∴ The points are (2,\(\frac{5}{3},\))(-2 -1)
R is true.

Question 5.
Assertion (A): At x =\(\frac{π}{6}\), the curve y = 2cos² (3x) has a vertical tangent.
Reason (R): The slope of tangent to the curve
y = 2cos² (3x) at x = \(\frac{π}{6}\) is zero.
Answer:
(D) A is false and R is True

Explanation:
Given y = 2cos²(3x)
\(\frac{π}{6}\) = 2 × 2 × cos(3x) × (- sin 3x) x 3
\(\frac{dy}{dx}\) = -6 sin 6x
\(\left.\frac{d y}{d x}\right]_{x=\frac{\pi}{6}}\) = -6 sin π
= -6 × 0
= 0
∴ R is true.
Since the slope of tangent is zero, the tangent is parallel to the X – axis. That is the curve has a horizontal tangent at x = \(\frac{π}{6}\) Hence A is false.

Question 6.
Assertion (A): The equation of tangent to the curve y = sin x at the point (0, 0) is y = x.
Reason(R): If y = sin x, then at x = 0 is 1.
Answer:
Option (A) is correct.

Explanation:
Given y = sin x
\(\frac{dy}{dx}\) = cos x
Slope of tangent at (0, 0) = \(\left[\frac{d y}{d x}\right]_{(0,0)}\)
= cos 0° = 1
∴ R is true.
Equation of tangent at (0, 0) is
y – 0 = 1(x – 0)
y = x.
Hence A is true.
R is the correct explanation of A.

Question 7.
Assertion (A): The slope of normal to the curve x² + 2y + y² = 0 at (-1, 2) is -3.
Reason (R): The slope of tangent to the curve x² + 2y + y² = 0 at(- 12) is
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:
Given x² + 2y + y² = 0
2x + 2\(\frac{dy}{dx}\) + 2y\(\frac{dy}{dx}\) = 0
\(\frac{dy}{dx}\) (2 + 2y) = -2x
\(\frac{dy}{dx}\) = \(\frac{-2 x}{2(1+y)}\) = \(\frac{-2 x}{2(1+y)}\) = \(\frac{x}{1+y}\)
Slope of tangent at (-1, 2)
\(\left[\frac{d y}{d x}\right]_{(-1,2)}=\frac{-(-1)}{1+2}\) = \(\frac{1}{3}\)
Hence R is true.
Slope of normal at (-1, 2)
= \(\frac{-1}{\text { Slope of tangent }}\)
Slope of tangent
= -3.
Hence A is true.
R is the correct explanation for A.

Question 8.
The equation of tangent at (2, 3) on the curve y² = ax³ + b is = 4x – 5.
Assertion (A): The value of a is ±2
Reason (R): The value of h is ±7
Answer:
(C) A is true but R is false

Explanation:
∴ y² = ax³ + b
Differentiate with respect to x,
2y \(\frac{dy}{dx}\) = 3a x²
or \(\frac{dy}{dx}\) = \(\frac{3 a x^{2}}{2 y}\)
or \(\frac{dy}{dx}\) = \(\frac{3 a x^{2}}{\pm 2 \sqrt{a x^{3}+b}}\) [∴ y² = ax³ + b]
or \(\left.\frac{d y}{d x}\right|_{(2,3)}=\frac{3 a(2)^{2}}{\pm 2 \sqrt{a(2)^{3}+b}}\)
= \(\frac{12 a}{\pm 2 \sqrt{8 a+b}}\)
= \(\frac{6 a}{\pm \sqrt{8 a+b}}\)
Since (2, 3) lies on the curve
y² = ax³ + b
or 9 – 8a + b ………..(1)
Also from equation of tangent
y = 4x – 5
slope of the tangent = 4
\(\left.\frac{d y}{d x}\right|_{(2,3)}=\frac{6 a}{\pm \sqrt{8 a+b}}\) becomes
4 = \(\frac{6 a}{\pm \sqrt{9}}\) {from(i)}
4 = \(\frac{6 a}{\pm 3}\)
4 = \(\frac{6 a}{ 3}\) or 4 = \(\frac{6 a}{-3}\)
either, a = 2 or a = -2
For a = 2,
9 = 8(2) + b
or b = -7
a = 2 and b = -7
and for a = -2,
9 = 8(-2) + b
or b = 25
or a = -2 and b = 25
Hence A is true and R is false.

Question 9.
Assertion (A): The function f(x) = x³ – 3x² + 6x -100 is strictly increasing on the set of real numbers.
Reason (R): A strictly increasing function is an injective function.
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A

Explanation:
f(x) = x³ – 3x² + 6x – 100
f'(x) = 3x² – 6x + 6
= 3[x² – 2x + 2]
= 3[(x – 1)² + 1]
since f'(x) > 0; x ∈R
f(x) is strictly increasing on R.
Hence A is true.
For a strictly increasing function,
x₁ > x₂
f(x₁) > f(x₂)
i.e.; x₁ = x₂
= f(x₁) = f(x₂)
Hence, a strictly increasing function is always an injective function.
So R is true.
But R is not the correct explanation of A.

Question 10.
Consider the functionf(x) = sin4x + cos4x.
Assertion (A): f(x) is increasing in[0,\(\frac {π}{4}\) ]
Reason (R): f(x) is decreasing in [\(\frac {π}{2}\),\(\frac {π}{4}\)]
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A

Explanation:
f(x) = sin⁴ x + cos⁴ x
or f'(x) = 4sin³x cos x – 4 cos³x sin x
= – 4sin x cos x – sin² x + cos² xJ
= -2 sin 2x cos 2x
= -sin 4x
On equating,
f'(x) = 0
or -sin 4x = 0
or 4x = 0,π,2π,………….
or x = 0,\(\frac{\pi}{4}, \frac{\pi}{2}\)
Sub-intervals are [0,\(\frac {π}{4}\)],\(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\)
or f'(x)< o in [o. \(\left[0, \frac{\pi}{4}\right]\) or f(x) is decreasing in [o, \(\left[0, \frac{\pi}{4}\right]\) and f’(x) > 0 in \(\frac{\pi}{4}, \frac{\pi}{2}\)
∴ f'(x) is increasing in [latex]\frac{\pi}{4}, \frac{\pi}{2}[/latex].
Both A and R are true. But R is not the correct explanation of A.

Question 11.
Assertion (A): The function y = [x(x – 2)²] is increasing in (0, 1) ∪ (2,∞ )
Reason (R): = \(\left[0, \frac{\pi}{4}\right]\) = 0, when x = 0, 1,2.
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A

Explanation:
y = [x(x – 2)]²
= [x² – 2x]²
∴ \(\frac{d y}{d x}\) = 2(x² – 2x)(2x – 2)
∴ \(\frac{d y}{d x}\) = 4x(x – 1)(x – 2)
On equating \(\frac{d y}{d x}\) = 0
4x(x – 1)(x – 2) = 0
⇒x = 0,.x = 1,x = 2
∴ intervals are (-∞, 0), (0,1), (1,2), (2,∞)
Since, \(\frac{d y}{d x}\) > 0 in (0,1) or (2, ∞)
∴ f(x) is increasing in (0,1) u (2, ∞)
Both A and R are true. But R is not the correct explanation of A.

Question 12.
Assertion (A): The function y = log(1 + x) – 2 + x is a decreasing function of x throughout its domain.
Reason (R): The domain of the function
f(x) = log(1 + x) 2 + x (-1, c)
Answer:
(D) A is false and R is True

Explanation:
log (1 + x) is defined only when x + 1 > 0 or x > -1

Hence R is true.
y = log(1 + x) – \(\frac{2 x}{2+x}\)
Duff. w.tt. ‘x’,
\(\frac{d y}{d x}=\frac{1}{1+x}-\frac{[(2+x)(2)-2 x]}{(2+x)^{2}}\)
= \(\frac{1}{1+x}-\frac{[4-2 x-2 x]}{(2+x)^{2}}\)
= \(\frac{1}{1+x}-\frac{4}{(2+x)^{2}}\)
= \(\frac{(2+x)^{2}-4(1+x)}{(2+x)^{2}(1+x)}\)
= \(\frac{4+x^{2}+4 x-4-4 x}{(2+x)^{2}(1+x)}\)
= \(\frac{x^{2}}{(2+x)^{2}(1+x)}\)
For increasing function,
\(\frac{x^{2}}{(2+x)^{2}(1+x)}\) ≥ 0
or \(\frac{x^{2}}{(2+x)^{2}(x+1)}\) ≥ 0
or \(\frac{(2+x)^{2}(x+1) x^{2}}{(2+x)^{4}(x+1)^{2}}\) ≥ 0
or \((2+x)^{2}(x+1) x^{2}\) ≥ 0
When x > -1,
\({dy}{dx}\) is always greater than zero.
∴ y = log(l + x) – \(\frac{2 x}{2+x}\)
is always increasing throughout its domain.
Hence A is false.

Question 13.
The sum of surface areas (S) of a sphere of radius ‘r’ and a cuboid with sides \(\frac{x}{3}\), x and 2x is a constant.
Assertion (A): The sum of their volumes (V) is minimum when x equals three times the radius of the sphere.
Reason (R): Vis minimum when r = \(\sqrt{\frac{S}{54+4 \pi}}\)
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:
Given S = 4πr² + 2\(\left[\frac{x^{2}}{3}+2 x^{2}+\frac{2 x^{2}}{3}\right]\)
S = 4πr² + 6x²
or x² = \(\frac{S-4 \pi r^{2}}{6}\)
and V = \(\frac{4}{3} \pi r^{3}+\frac{2 x^{3}}{3}\)
V = \(\frac{4}{3} \pi r^{3}+\frac{2}{3}\left(\frac{S-4 \pi r^{2}}{6}\right)^{3 / 2}\)
\(\frac{d V}{d r}=4 \pi r^{2}+\left(\frac{S-4 \pi r^{2}}{6}\right)^{1 / 2}\left(\frac{-8 \pi r}{6}\right)\)
\(\frac{dV}{dr}\) = 0
or r = \(\sqrt{\frac{S}{54+4 \pi}}\)
Now \(\frac{d^{2} V}{d r^{2}}=8 \pi r+\left(\frac{-8 \pi}{6}\right)\left(\frac{S-4 \pi r^{2}}{6}\right)^{1 / 2}\) + \(\frac{1}{2}\left(\frac{S-4 \pi r^{2}}{6}\right)^{-1 / 2}\left(\frac{-8 \pi r}{6}\right)\)
at r = \(\sqrt{\frac{S}{54+4 \pi}} ; \frac{d^{2} V}{d r^{2}}>0\)
∴ for r = \(\sqrt{\frac{S}{54+4 \pi}}\) volume is minimum
i.e., r²(54 + 4π) = S
or r² (54 + 4π) =4πr² + 6x²
or 6x² = 54r²
or x² = 9r²
or x = 3r
Hence both A and R are true.
R is the correct explanation of A.

Question 14.
AB is the diameter of a circle and C is any point on the circle.
Assertion (A): The area of ΔABC is maximum when it is isosceles.
Reason (R): ΔABC is a right-angled triangle.
Answer:
(A) Both A and R are true and R is the correct explanation of A

Explanation:

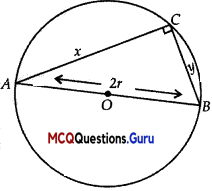
Let the sides of rt. ∆ABC be x and y.
∴ x² + y² = 4r²
and A = Area of ∆ = \(\frac {1}{2}\) xy
Let, S = A² = \(\frac {1}{2}\) x²y²
= \(\frac {1}{4}\) x²(4r² – x²)
= \(\frac {1}{4}\)(4r²x² – x⁴
∴ \(\frac {dS}{dx}\) = \(\frac {1}{4}\)\(\left[8 r^{2} x-4 x^{3}\right]\)
or \(\frac {dS}{dx}\) = 0
or x² = 2r² or x = \(\sqrt{2} r\)
and y² = 4r² – 2r² = 2r²
or y = \(\sqrt{2} r\)
i.e., x = y and \(\frac{d^{2} S}{d x^{2}}\) = (2r² – 3x²)
= 2r² – 6r²<0
or Area is maximum, when à is isosceles.
Hence A is true.
Angle in a semicircle is a right angle.
∴ ∠C = 90°
∆ABC is a right-angled triangle.
∴ R is true.
R is the correct explanation of A.

Question 15.
A cylinder is inscribed in a sphere of radius R.
Assertion (A): Height of the cylinder of maximum volume is \(\frac{2 R}{\sqrt{3}}\) units.
Reason (R): The maximum volume of the cylinder is \(\frac{2 R}{\sqrt{3}}\) cubic units.
Answer:
(C) A is true but R is false

Explanation:
Let the radius and height of cylinder be r and h respectively
∴V = πr²h ………..(1)
But r² = R² – \(\frac{h^{2}}{4}\)
∴ \(\pi h\left(R^{2}-\frac{h^{2}}{4}\right)=\pi\left(R^{2} h-\frac{h^{3}}{4}\right)\)
or \(\frac{d V}{d h}=\pi\left(R^{2}-\frac{3 h^{2}}{4}\right)\)
For maximum or minimum
∴ \(\frac{d V}{d h}=0 \text { or } h^{2}=\frac{4 R^{2}}{3}\)
or h = \(\frac{2 R}{\sqrt{3}}\)

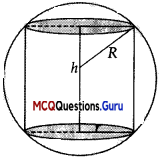
and \(\frac{d^{2} V}{d h^{2}}=\pi\left(-\frac{6 h}{4}\right)<0\)
Maximum volume = \(\pi \cdot\left[R^{2} \cdot \frac{2 R}{\sqrt{3}}-\frac{1}{4}\left(\frac{2 R}{\sqrt{3}}\right)^{3}\right]\)
= \(\frac{4 \pi R^{3}}{3 \sqrt{3}}\) cubic units
Hence A is true and R is false.

Question 16.
Assertion (A): The altitude of the cone of maximum volume that can be inscribed in a sphere of radius r is \(\frac{4 r}{3}\)
Reason (R): The maximum volume of the cone is \(\frac{8}{7}\) of the volume of the sphere.
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A

Explanation:
Let radius ‘of cone be x and its height be h.
∴ OD = (h – r)
Volume of cone
(V) = \(\frac{1}{3} \pi x^{2} h\) …………(1)

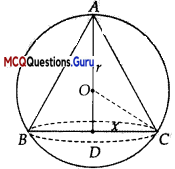
In ∆OCD, x² + (h – r)² = r² or x² = r² – (h – r)²
∴ V = \(\frac{1}{3}\)πh {r² – (h – r)²}
= \(\frac{1}{3}\)π(- h³ + 2h²r)
or \(\frac{d V}{d h}=\frac{\pi}{3}\left(-3 h^{2}+4 h r\right)\)
∴ \(\frac{d V}{d h}=0 \text { or } h=\frac{4 r}{3}\)
\(\frac{d^{2} V}{d h^{2}}=\frac{\pi}{3}(-6 h+4 r)\)
= \(\frac{\pi}{3}\left(-6\left(\frac{4 r}{3}\right)+4 r\right)\)
= \(-\frac{4 \pi r}{3}<0\)
∴ at h = \(-\frac{4 \pi r}{3}<0\) Volume is maximum

Maximum volume
= \(\frac{1}{3} \pi \cdot\left\{-\left(\frac{4 r}{3}\right)^{3}+2\left(\frac{4 r}{3}\right)^{2} r\right\}\)
= \(\frac{8}{27} \cdot\left(\frac{4}{3} \pi r^{3}\right)\)
= \(\frac{8}{27}\) (volume of sphere)
Hence both A and R are true.
R is not the correct explanation of A.

Case-Based MCQs

Attempt any four sub-parts from each question.
Each sub-part carries 1 mark.

I. Read the following text and answer the following questions, on the basis of the same:
The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – \(\frac {1}{2}\) x² where x is the number of days exposed to sunlight.

Question 1.
The rate of growth of sunlight is …………..
(A) 4x – \(\frac {1}{2}\) x²
(B) 4 – x
(C) x – 4
(D) x – \(\frac {1}{2}\)x²
Answer:
(B) 4 – x

Explanation:
y = 4x – \(\frac {1}{2}\) x²
rate of growth of the pIant with respect to sunlight.
= \(\frac {dy}{dx}\)
= \(\frac {d}{dx}\)\(\left[4 x-\frac{1}{2} x^{2}\right]\)
= (4 – x)cm/day

Question 2.
What is the number of days it will take for the plant to grow to the maximum height?
(A) 4
(B) 6
(C) 7
(D) 10
Answer:
(A) 4

Explanation:
\(\frac {dy}{dx}\) = 4 – x
The number of days it will take for the plant to grow to the maximum height,
\(\frac {dy}{dx}\) = 0
4 – x = 0
x = 4 Days.

Question 3.
What is the maximum height of the plant?
(A) 12 cm
(B) 10 cm
(C) 8 cm
(D) 6 cm
Answer:
(C) 8 cm

Explanation:
We have, number of days for maximum height of plant = 4 Days
∴ Maximum height of plant
\(y_{(x=4)}\) = 4 x 4 – \(\frac {1}{2}\) x 4 x 4 = 16 – 8 = 8 cm

Question 4.
What will be the height of the plant after 2 days?
(A) 4 cm
(B) 6 cm
(C) 8 cm
(D) 10 cm
Answer:
(B) 6 cm

Explanation:
Height of plant after 2 days
\(y_{(x=4)}\) = 4 x 2 – \(\frac {1}{2}\) x 2 x 2 = 8 – 2= 6 cm

Question 5.
If the height of the plant is 7/2 cm, the number of days it has been exposed to the sunlight is ………….
(A) 2
(B) 3
(C) 4
(D) 1
Answer:
(D) 1

Explanation:
Given, y = \(\frac {7}{2}\)
i.e., 4x – \(\frac {1}{2}\) x² = \(\frac {7}{2}\)
8x – x² = 7
x² – 8x + 7 = 0
x² – 7x – x + 7 = 0
x(x – 7) – (x – 7) = 0
x = 17
We will take x = 1, because it will take 4 days for the plant to grow to the maximum height i.e. 8 cm and cm is not maximum height so, it will take less than 4 days. i.e., 1 Day.

II. Read the following text and answer the following
questions on the basis of the same:
P(x) = – 5x² + 125 x + 37500 is the total profit function of a company, where x is the production of the company.

Question 1.
What will be the production when the profit is maxi mum?
(A) 37,500
(B) 12.5
(C) – 12.5
(D) – 37,500
Answer:
(B) 12.5

Explanation:
We, have
P(x) = – 5x² + 125x + 37500
P(x) = – 10x + 125
For maximum profit
P'(x) = 0
– 10 x + 125 = O
– 10 x = -125
x = \(\frac {125}{10}\)
= 12.5

Question 2.
What will he the maximum profit?
(A) ₹ 38,28,125
(B) ₹ 38,281.25
(C) ₹ 39,0(X)
(D) None of these
Answer:
(B) ₹ 38,281.25

Explanation:
Maximum profit
= P (1Z5)
= – 5(12.5)² + 125 x 12.5 + 37500
= -781.25 + 1562.5 + 37500
= 38,281.25

Question 3.
Check-in which interval the profit is strictly increasing.
(A) (12.5, o)
(B) for all real numbers
(C) for all positive real numbers
(D) (0, 12.5)
Answer:
(D) (0, 12.5)

Question 4.
When the production is 2 units what will be the profit of the company?
(A) 37,500
(B) 37,730
(C) 37,770
(D) None of these
Answer:
(B) 37,730

Explanation:
When production is 2 units, then profit of company = P(2)
= -5 × 2² +125 × 2 + 37500
= -20 + 250 + 3700
= 37,730

Question 5.
What will be production of the company when the profit is ₹ 38,250 ?
(A) 15
(B) 30
(C) 10
(D) data is not sufficient to find
Answer:
(C) 10

Explanation:
Profit = 38,250
i.e., -5x² + 125x +37,500 = 38,250
5x² – 125x + 750 = 0
x² – 25x + 150 = 0
x(x – 15)-10 (x – 15) = 0
(x – 10) (x -15) = 0
x = 10,15
P(x) = -5x² + 125x + 37500
P(10) = 5 x 10² + 125 x 10 + 37500
= – 500 + 1250 + 37500
= ₹ 38,250
Hence, production of company is 10 units when the profit is ₹ 38250.

III. Read the following text and answer the following questions on the basis of the same:
The shape of a toy is given as f(x) = 6(2x⁴ – x²). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

Question 1.
Which value from the Following may be abscissa ot critical point?
(A) ± 1/4
(B) ± 12
(C) ± 1
(D) None of these
Answer:
(B) ± 12

Question 2.
Find the slope of the normal based on the position of the stick.
(A) 360
(B) -360
(C) \(\frac {1}{360}\)
(D) \(\frac {-1}{360}\)
Answer:
(D) \(\frac {-1}{360}\)

Explanation:
Slope of the normal based on the position of the slick
= \(\frac{-1}{f^{\prime}(x)}\)
f'(x) = 6 [8x³ – 2x]
f'(2) = 6[8 x 8 – 2 x 2]
= 6[64 – 4]
= 360
∴ Slope = \(\frac {1}{360}\)

Question 3.
What will be the equation of the tangent at the critical point ¡fit passes through (2, 3)?
(A) x + 360 y = 1082
(B) y = 360 x – 717
(C) x = 717y + 360
(D) None of these
Answer:
(B) y = 360 x – 717

Explanation:
We have
\(\left.\frac{d y}{d x}\right]_{(2,3)}\) = 360
∴ (y – y’) = \(\frac{d y}{d x}\) (x – x’)
(y – 3) = 360(x – 2)
y – 3 = 360x – 720
y = 360x – 717

Question 4.
Find the second-order derivative of the function at x = 5.
(A) 598
(B) 1,176
(C) 3,588
(D) 3,312
Answer:
(C) 3,588

Explanation:
f(x) =6(2⁴ – x²)
f'(x) = 6[8x³ – 2x]
f”(x) = 6[24x² – 2]
f”(5) = 6[24 x 25 – 2]
= 6[600 – 2]
= 3588

Question 5.
At which of the following intervals will f(x) be increasing?
(A) \(\left(-\infty, \frac{-1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
(B) \(\left(\frac{-1}{2}, 0\right) \cup\left(\frac{1}{2}, \infty\right)\)
(C) \(\left(0, \frac{1}{2}\right) \cup\left(\frac{1}{2}, \infty\right)\)
(D) \(\left(-\infty, \frac{-1}{2}\right) \cup\left(0, \frac{1}{2}\right)\)
Answer:
(B) \(\left(\frac{-1}{2}, 0\right) \cup\left(\frac{1}{2}, \infty\right)\)

Explanation:
For increasing
f'(x) > 0
6(8x³ – 2x) > 0
i.e., x(4x² – 1) > 0
4x² – 1 > 0
x > 0
4x² >1
x² > \(\frac {1}{4}\)
x > \(\frac {1}{2}\)
and x >\(\frac {1}{2}\)
i.e., x ∈\(\left(\frac{-1}{2}, 0\right) \cup\left(\frac{1}{2}, \infty\right)\)

VI. Read the following text and answer the following questions, on the basis of the same:
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:

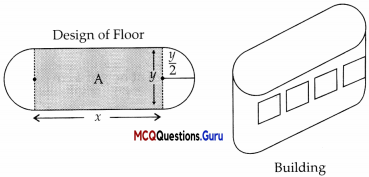
Question 1.
11 x and y represents the length and breadth of the rectangular region, then the relation between the variables is:
(A) x + πy = 100
(B) 2x + πy = 200
(C) πx + y = 50
(D) x + y = 100
Answer:
(B) 2x + πy = 200

Explanation:
Perimeter =
x + x + \(\frac{\pi y}{2}+\frac{\pi y}{2}\)
200 = 2x + \(\frac{2 \pi y}{2}\)
200 = 2x + πy

Question 2.
The area of the rectangular region A expressed as a function of x is :
(A) \(\frac {2}{π}\) (100 x – x²)
(B) \(\frac {1}{π}\) (100x – x²)
(C) \(\frac {x}{π}\) (100x – x)
(D) πy² + \(\frac {1}{π}\) (100x – x²)
Answer:
(A) \(\frac {2}{π}\) (100 x – x²)

Explanation:
Area (A) = x × y
= x × \(\left(\frac{200-2 x}{\pi}\right)\) [from (i)]
\(\frac {2}{π}\) [100x – x²] ………(i)

Question 3.
The maximum value of area A is:
(A) \(\frac{\pi}{3200}\) m²
(B) \(\frac{\pi}{3200}\) m²
(C) \(\frac{\pi}{5000}\) m²
(D) \(\frac{\pi}{1000}\) m²
Answer:
(C) \(\frac{\pi}{5000}\) m²

Explanation:
\(\frac{dA}{dx}\) = \(\frac{2}{π}\) [100 – 2x]
\(\frac{dA}{dx}\) = \(\frac{2}{π}\) [500 – 2x]
\(\frac{dA}{dx}\) = 0
x = 50 ………(i)
A = \(\frac{2}{π}\)[ 100 × 50 – 50 × 50]
= \(\frac{2}{π}\) [5000 – 2500]
= \(\frac{2}{π}\) x 2500
= \(\frac{2}{5000}\) m²

Question 4.
The CEO of the multi-national company is interested in maximizing the area of the whole floor including the semi-circular ends. For this to happen
the value of x should be
(A) 0 m
(B) 30 m
(C) 50 m
(D) 80 m
Answer:
(A) 0 m

Question 5.
The extra area generated if the area of the whole floor is maximized is:
(A) \(\frac{3000}{π}\) m²
(B) \(\frac{5000}{π}\) m²
(C) \(\frac{7000}{π}\) m²
(D) No change. Both areas are equal.
Answer:
(D) No change. Both areas are equal.

V. Read the following text and answer the following questions. On the basis of the same:
An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the
sides.

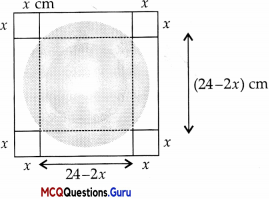
Question 1.
Find the volume of that open box?
(A) 4x² – 96x² + 576x
(B) 4x³ + 96x² – 576x
(C) 2x³ – 48x² + 288x
(D) 2x³ + 48x² + 288x
Answer:
(A) 4x² – 96x² + 576x

Explanation:
Volume of open box = length × breadth × height
= (24 – 2x) × (24 – 2x)
= (4x³ – 96x² + 576x) cm³

Question 2.
Find the value of \(\frac{dV}{dx}\)
(A) 12(x² + 16x – 48)
(B) 12(x² – 16x + 48)
(C) 6(x² + 8x – 24)
(D) 6(x² – 8x + 24)
Answer:
(B) 12(x² – 16x + 48)

Explanation:
\(\frac{dV}{dx}\) = \(\frac{d}{dx}\)[4x² – 96x² + 576x]
= 12x² – 2 × 96x + 576
= 12 [r² – 16x + 48]

Question 3.
Find the value of \(\frac{d^{2} \mathrm{~V}}{d x^{2}}\) ?
(A) 24(x + 8)
(B) 12(x – 4)
(C) 24(x – 8)
(D) 12(x + 4)
Answer:
(C) 24(x – 8)

Explanation:
\(\frac{d^{2} \mathrm{~V}}{d x^{2}}\) = \(\frac{d}{d x}\left[\frac{d V}{d x}\right]\)
\(\frac{d}{d x}\left[12\left(x^{2}-16 x+48\right)\right]\)
= [12 (2x – 16)]
= 24(x – 8)

Question 4.
Find the value of x other than 12?
(A) 3
(B) 9
(C) 1
(D) 4
Answer:
(D) 4

Question 5.
Volume is maximum at what height of that open box?
(A) 3 cm
(B) 9 cm
(C) 1 cm
(D) 4 cm
Answer:
(D) 4 cm

Explanation:
For maximum value,
\(\frac {dV}{dx}\) = 0
i.e.,12(x² – 16x + 48) = 0
x² – 16x + 48 = 0
x² – 4x – 12x + 48 = 0
x(x – 4) -12(x – 4) = 0
(x – 4(x – 12) = 0
x = 4,12
V(x = 4) = (24 – 2 × 4)(24 – 2 × 4) × 4
= 16 × 16 × 4
= 1024 cm³
V(x = 12) = (24 – 2 × 12)(24 – 2 × 12) × 12 = 0
Hence, volume is maximum at height 4 cm of the open box.

VI. Read the following text and answer the following questions on the basis of the same:
A right circular cylinder is inscribed in a cone.

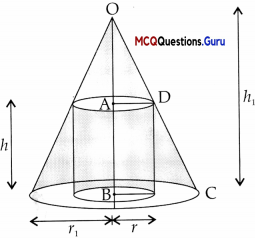
S = Curved Surface Area of Cylinder.
Question 1.
\(\frac{r}{r_{1}}\) = ?
(A) \(\frac{h-h_{1}}{h_{1}}\)
(B) \(\frac{h_{1}-h}{h_{1}}\)
(C) \(\frac{h-h_{1}}{h}\)
(D) \(\frac{h+h_{1}}{h_{1}}\)
Answer:
(B) \(\frac{h_{1}-h}{h_{1}}\)

Explanation:
In ∆DEC and ∆OBC [Since DEC 1OBC]
\(\frac{D E}{O B}=\frac{E C}{B C}\)
\(\frac{h}{h_{1}}=\frac{r_{1}-r}{r_{1}}\)
r₂h = r₁h₁ – rh₁
r₁(h – h₁) = – rh₁
or \(\frac{r}{r_{1}}=\frac{h_{1}-h}{h_{1}}\)

Question 2.
Find the value of ‘S’?
(A) \(\frac{2 \pi r}{h}\left(h_{1}-h\right) h\)
(B) \(\frac{2 \pi r}{h_{1}}\left(h_{1}-h\right) h\)
(C) \(\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}-h\right) h\)
(D) \(\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}+h\right) h\)
Answer:
(C) \(\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}-h\right) h\)

Explanation:
Curved surface area of cylinder,
s = \(\frac{2 \pi r}{r_{1}}\left(r_{1}-r\right) h_{1}\)
= \(2 \pi r h_{1} \times \frac{h}{h_{1}}\) [∴ \(\frac{h}{h_{1}}=\frac{r_{1}-r}{r_{1}}\)]
= \(\frac{2 \pi r_{1}\left(h_{1}-h\right) \cdot h}{h_{1}}\) [∴ \(r=r_{1} \frac{\left(h_{1}-h\right)}{h_{1}}\)]
∴ S = \(\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}-h\right) h\)

Question 3.
What is the value of \(\frac {dS}{dh}\) ?
(A) \(\frac{2 \pi r_{1}}{h}\left(h_{1}-2 h\right)\)
(B) \(\frac{2 \pi r_{1}}{h_{1}}\left(h-2 h_{1}\right)\)
(C) \(\frac{2 \pi r}{h}\left(h_{1}-2 h\right)\)
(D) \(\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}-2 h\right)\)
Answer:
(D) \(\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}-2 h\right)\)

Explanation:
\(\frac{d S}{d h}=\frac{2 \pi r_{1}}{h_{1}}\left(h_{1}-2 h\right)\)

Question 4.
Find the value of \(\frac{d^{2} \mathrm{~S}}{d h^{2}}\)?
(A) \(-\frac{4 \pi r_{1}}{h_{1}}\)
(B) \(-\frac{4 \pi r}{h}\)
(C) \(-\frac{4 \pi r_{1}}{h}\)
(D) \(\frac{4 \pi r_{1}}{h}\)
Answer:
(A) \(-\frac{4 \pi r_{1}}{h_{1}}\)

Explanation:
\(\frac{d^{2} S}{d h^{2}}=\frac{2 \pi r_{1}}{h_{1}}(0-2)\)
= \(\frac{-4 \pi r_{1}}{h_{1}}\)

Question 5.
What is the relation between r1 and r?
(A) r₁ = \(\frac {r}{2}\)
(B) 2r₁ = 3r
(C) r₁ = 2r
(D) \(\frac{r_{1}}{2}=\frac{r}{3}\)
Answer:
(C) r₁ = 2r

Explanation:
S = \(\frac{2 \pi r}{r_{1}}\left(r_{1}-r\right) h_{1}\)
S = \(\frac{2 \pi h_{1}\left(r r_{1}-r^{2}\right)}{r_{1}}\)
\(\frac {dS}{dr}\) = \(\frac{2 \pi h_{1}\left(r_{1}-2 r\right)}{r_{1}}\)
\(\frac {dS}{dr}\) = 0
\(\frac{2 \pi h_{1}\left(r_{1}-2 r\right)}{r_{1}}\) = 0
r₁ – 2r = 0
r₁ = 2r

MCQ Questions for Class 12 Maths with Answers