CBSE Class 9

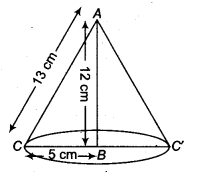
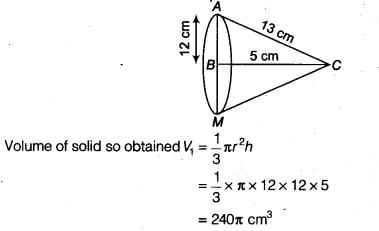
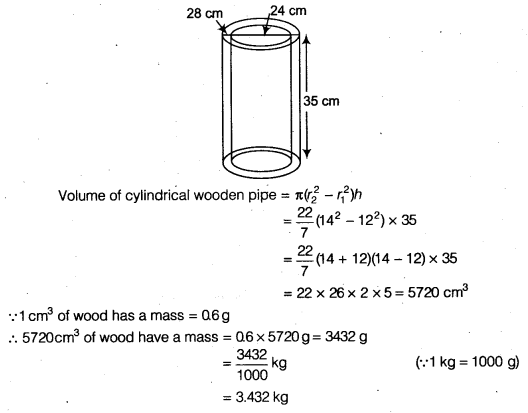
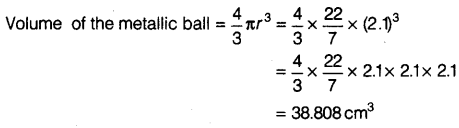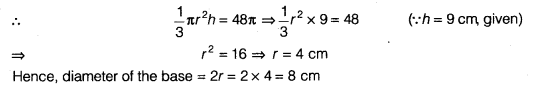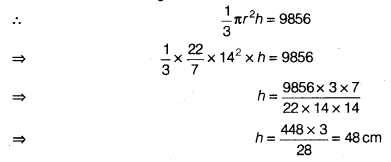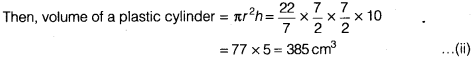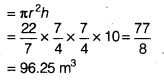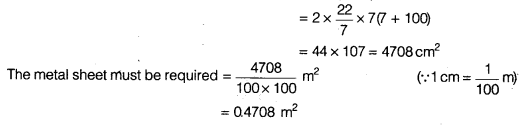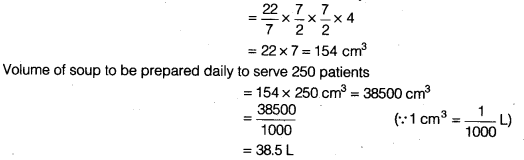NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9

Question 1.
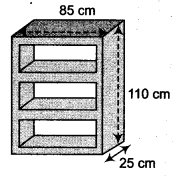
A wooden bookshelf has external dimensions as follows : Height = 110cm, Depth = 25cm, Breadth = 85cm (see figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing-is 20 paise per cm² and the rate of pointing is 10 paise per cm², find the total expenses required for palishing and painting the surface of the bookshelf.

Solution:
Here, l = 85 cm b = 25 cm and h = 110 cm
Area of the bookshelf of outer surface = 2 lb + 2bh + hl
= [2(85 x 25)+ 2(110 x 25)+ 85×110] cm2 = (4250 + 5500 + 9350) cm² = 19100 cm²
Cost of polishing of the outer surface of bookshelf
= 19100 x \(\frac { 20 }{ 100 }\) = ₹ 3820
Thickness of the plank = 5 cm
Internal height of bookshelf = (110 – 2 x 5) = 100 cm
Internal depth of bookshelf = (25 – 5) = 20 cm
Internal breadth of bookshelf = 85 – 2 x 5 = 75 cm
Hence, area of the internal surface of bookshelf
= 2(75 x 20)+ 2(100x 20)+ 75×100
= 3000 + 4000 + 7500 = 14500 cm2
So, cost of painting of internal surface of bookshelf
= 14500 x \(\frac { 10 }{ 100 }\) = ₹1450
Hence, total costing of polishing and painting = 3820 + 1450= ₹ 5270

Question 2.
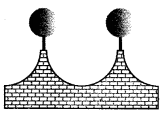
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in figure. Eight such spheres are-used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².

Solution:
It is obvious, we have to subtract the cost of the sphere that is resting on the supports while calculating the cost of silver paint.
Surface area to be silver paint

Question 3.
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
Solution:
Let d be the diameter of the sphere

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.8 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.8.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.8

Question 1.
Find the volume of a sphere whose radius is
(i) 7 cm
(ii) 0.63 cm
Solution:
(i) We have, r = 7 cm

Question 2.
Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm
(ii) 0.21 m
Solution:
(i) We have, d = 28 cm
⇒ r = 14 cm

Question 3.
The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm³?
Solution:
We have, d = 4.2 cm ⇒ r = 2.1 cm

The density of the metal per cm³ = 8.9 g
The density of the metal 38.808 cm³ = 38.808 x 8.9 g = 345.39 g
Hence, the mass of the ball = 345.39 g

Question 4.
The diameter of the Moon is approximately one-fourth of the diameter of the Earth. What fraction of the volume of the Earth is the volume of the Moon?
Solution:
Let diameter of the Earth is d₃.
We have, diameter of Moon (d₁) = \(\frac { 1 }{ 4 }\) diameter of the Earth

Question 5.
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Solution:
Diameter = 10.5 cm
⇒ Radius, r = 5.25 cm

Question 6.
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Solution:
Inner radius (r₁) = 1 m -100 cm
Outer radius (r₂) = (100 + 1)cm ( ∵ Inner radius + Thickness)
= 101 cm

Question 7.
Find the volume of a sphere whose surface area is 154 cm².
Solution:
We have, surface area of a sphere = 154 cm²

Question 8.
A dome of a building is in the form of a hemisphere. From inside, it was white washed at the cost of ₹498.96. If the cost of white washing is ₹2.00 per square metre, find the
(i) inside surface area of the dome,
(ii) volume of the air inside the dome.
Solution:
Cost of white washed = ₹ 498.96
Cost of white washing per square metre = ₹ 2.00

Question 9.
Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the
(i) radius r’ of the new sphere,
(ii) ratio of S and S’.
Solution:

Question 10.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm³) is needed to fill this capsule?
Solution:
We have, diameter = 3.5 mm

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.8 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.8, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7

Question 1.
Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
Solution:
(i) We have, r = 6 cm and h = 7cm

Question 2.
Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
Solution:
(i) We have, r = 7 cm and l = 25 cm

Question 3.
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use π = 3.14)
Solution:

Question 4.
If the volume of a right circular cone of height 9 cm is 48 cm3, find the diameter of its base.
Solution:
We have, volume of a right circular cone = 48 π cm3

Question 5.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Solution:
We have, diameter = 3.5 m

Question 6.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
Solution:
We have, d = 28cm
⇒ r = 14 cm
∵ Volume of a right circular cone = 9856 cm³

Question 7.
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
On revolving the right ∆ ABC about the side AB, we get a cone as shown in the adjoining figure.

∴ Volume of the solid so obtained = \(\frac { 1 }{ 3 }\) πr²h
= \(\frac { 1 }{ 3 }\) x π x 5 x 5 x 4 = 100π cm³
Hence, the volume of the solid so obtained is 100π cm³.

Question 8.
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
On revolving the right ∆ ABC about the side BC( = 5 cm),
we get a cone as shown in the adjoining figure.

In above Question 7, the volume V₂ obtained by revolving the ∆ ABC about the side 12 cm i.e., V₂ = 100π cm³.

Hence, the required ratio =5:12

Question 9.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Solution:

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6

Question 1.
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000cm3 =1 L.)
Solution:
We have, circumference of the base = 132 cm
∴ 2πr = 132

Question 2.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm³ of wood has a mass of 0.6 g.
Solution:
Given, inner diameter = 24 cm
Inner radius (r₁) = 12cm
Outer diameter = 28 cm
Outer radius (r₂) = 14cm
h = 35cm

Question 3.
A soft drink is available in two packs
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm.
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Solution:
(i) We have, h = 15cm
l = 5cm, b = 4cm, h = 15 cm
Volume of cuboidical body =l x b x h= 5 x 4 x 15 = 300cm3 …(i)
(ii) We have, Diameter = 7cm
Radius, r = \(\frac { 7 }{ 2 }\) cm
Height, h = 10cm

∴ From Eqs. (i) and (ii), we see that volume of a plastic cylinder has greater capacity and its capacity is 385 – 300 = 85 cm3 is more than the tin can.

Question 4.
If the lateral surface of a cylinder is 94.2 cm² and its height is 5 cm, then find
(i) radius of its base,
(ii) its volume. (Use π = 3.14)
Solution:
We have, lateral surface of a cylinder = 94.2 cm² and h = 5 cm
∴ 2πrh = 94.2
⇒ 2 x 3.14 x r x 5 = 94.2
⇒ r = \(\frac { 94.2 }{ 31.4 }\)
⇒ r = 3 cm
(i) Hence, radius of base, r = 3cm
(ii) Volume of a cylinder = πr2h= 3.14(3)²x 5
= 3.14 x 9 x 5
= 141.3 cm³

Question 5.
It costs ₹2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of ₹20 per m², find
(i) inner curved surface area of the vessel,
(ii) radius of the base,
(iii) capacity of the vessel.
Solution:
We have, cost to paint the inner curved surface = ₹2200
Cost to paint per m² = ₹20

(i) Inner curved surface area of the vessel = 110m²
(ii) Hence, radius of the base is 1.75 m.
(iii) Capacity of the vessel = Volume of the vessel

Question 6.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Solution:
Capacity of a closed cylindrical vessel = 15.4 L
= 15.4 x 1000cm3 (∵ 1L = 1000 cm²)
∴ πr²h = 15400 cm³
πr² x 100 = 15400
r² = 154 x \(\frac { 7 }{ 22 }\) (∵ h= 1m= 100cm)
⇒ r² = 7 x 7
⇒ r = 7 cm
Total surface area of closed cylindrical vessel = 2πr(r + h)

Question 7.
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of. the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution:

Question 8.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution:
We have, diameter = 7cm
Radius, r = \(\frac { 7 }{ 22 }\) cm
h= 4 cm
Capacity of the cylindrical bowl = Volume of the cylinder = πr²h

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5

Question 1.
A matchbox measures 4 cm x 2.5 cm x 1.5 cm. What will be the volume of a packet containing 12 such boxes?
Solution:
Volume of a match box = 4 cm x 2.5 cm x 1.5 cm= 15 cm³
Volume of a packet = 12 x 15 cm³ = 180 cm³

Question 2.
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold? ( 1 m³ = 1000L)
Solution:
Volume of a cuboidal water tank = 6 m x 5 m x 4.5 m
= 30 x 4.5 m³ = 135 m³
= 135 x 1000L = 135000L (∵ 1 m³ = 1000L)

Question 3.
A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid?
Solution:
Volume of a cuboidal vessel = hold liquid
∴ l x b x h = 380 m3
⇒ 10 x 8 x h = 380
⇒ h = \(\frac { 380 }{ 80 }\)
⇒ h= 4.75m
Hence, the cuboidal vessel must be made 4.75 m high.

Question 4.
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of ₹30 per m3.
Solution:
Volume of a cuboidal pit = l x bx h= (8 x 6 x 3)m³ =144 m³
∵ Cost of digging per m³ = ₹ 30
∴ Cost of digging 144m³ = ₹ 30x 144 = ₹ 4320

Question 5.
The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are 2.5 m and 10 m, respectively.
Solution:
Given, l = 2.5 m and h = 10m
Let breadth of tank be b.

Hence, breadth of the cuboidal tank is 2 m.

Question 6.
A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20 m x 15 m x 6 m. For how many days will the water of this tank last?
Solution:

Question 7.
A go down measures 40 m x 25 m x 10 m. Find the maximum number of wooden crates each measuring 15 m x 125 m x 0.5 m that can be stored in the go down.
Solution:
Dimension for godown, l = 40m b = 25 m and c = 10 m
Volume of the godown = l x b x h= 40 m x 25 m x 10 m
Dimension for wooden gate l = 1.5 m, b = 1.25 m, b = 1.25 m, h = 0.5 m
Volume of wooden gates = l x b x h = 1.5 m x 1.25 m x 0.5m

Question 8.
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution:
Volume of a solid cube = 12 cm x 12 cm x 12 cm = 1728 cm³
The solid cube is cut into eight cubes of equal volume.

Question 9.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
Solution:
Given, l = 2 km= 2 x 1000 m = 2000m
b = 40 m
and h = 3 m
Since, the water flows at the rate of 2 km h^-1,
i.e., the water from 2 km of river flows into the sea in one hour.
The volume of water flowing into the sea in one hour = Volume of the cuboid
= l x b x h
= (2000 x 40 x 3) m³
= 240000 m³
∴ The volume of water flowing into the sea in one minute
= \(\frac { 240000 }{ 60 }\) m³
= 4000 m³

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5, drop a comment below and we will get back to you at the earliest.