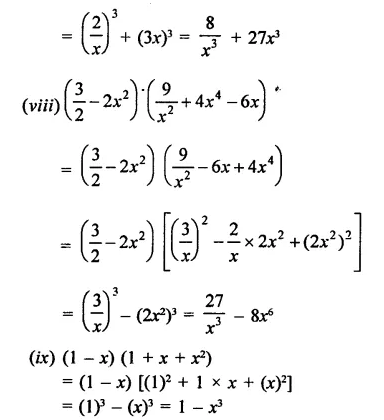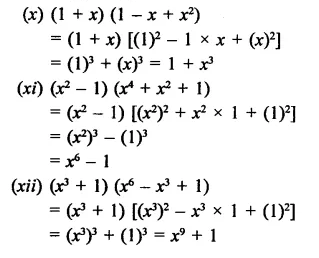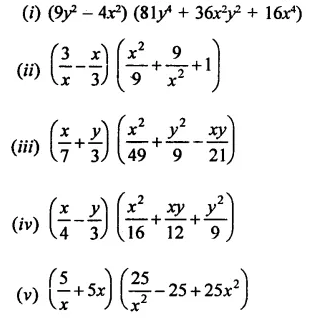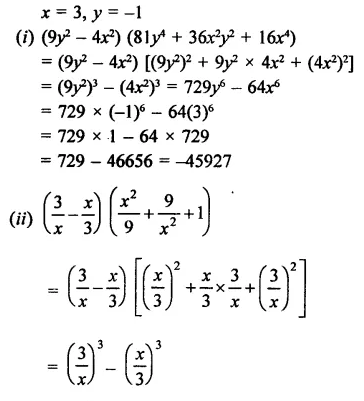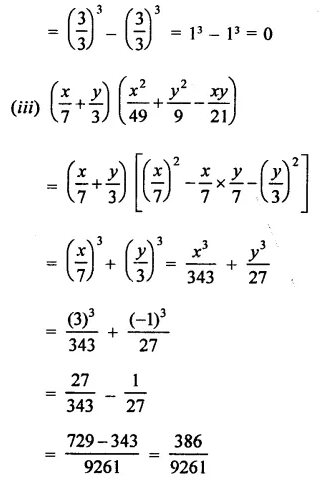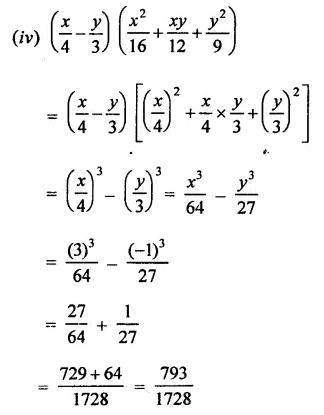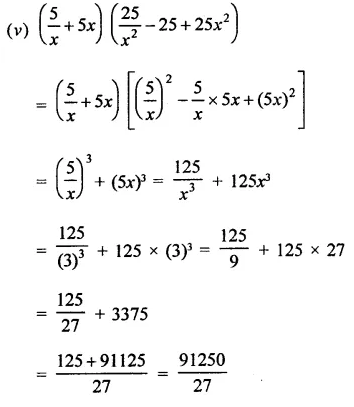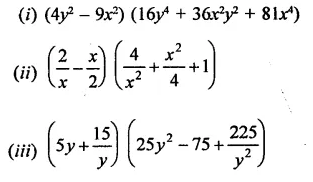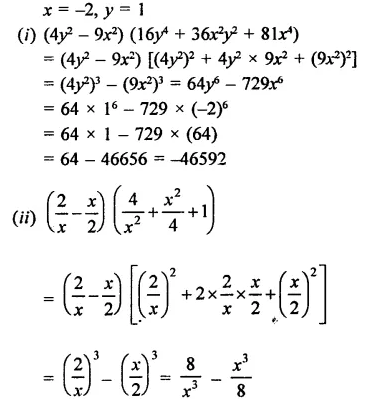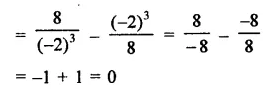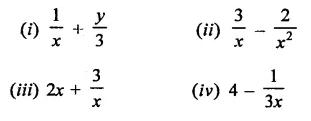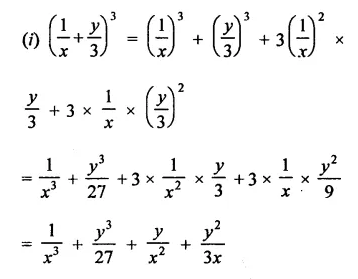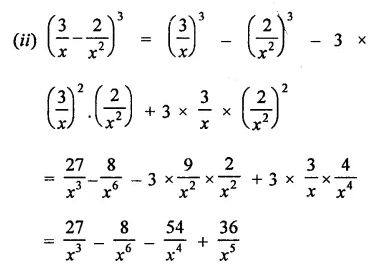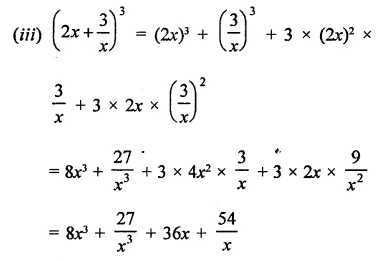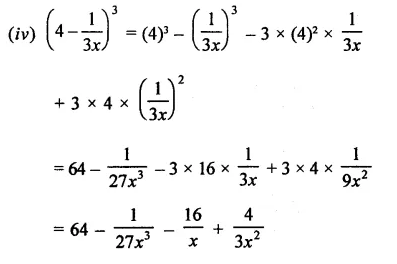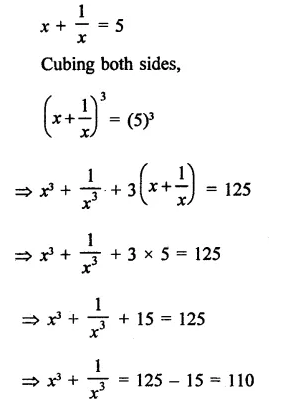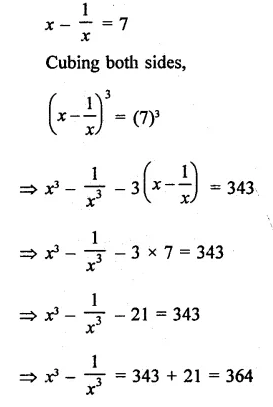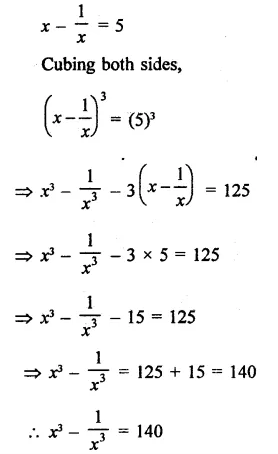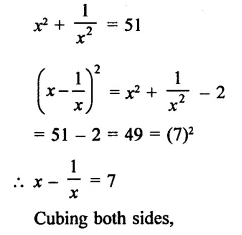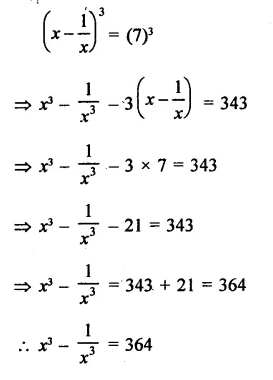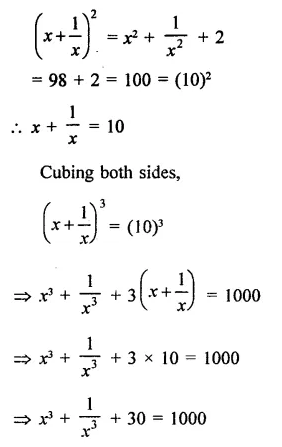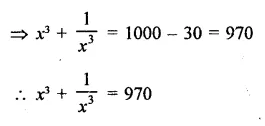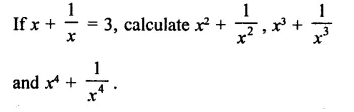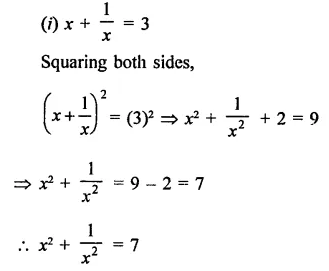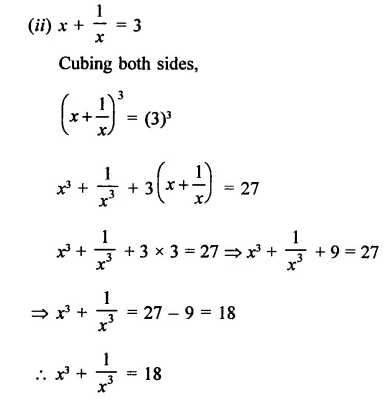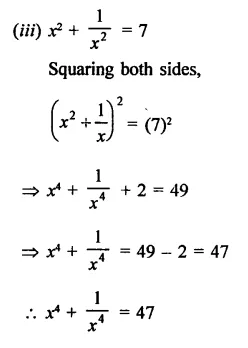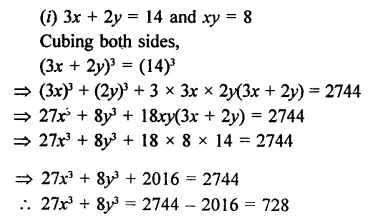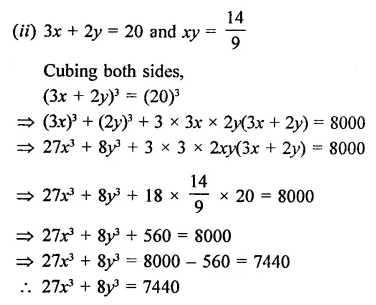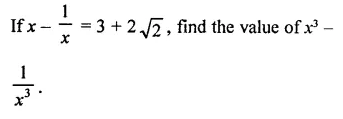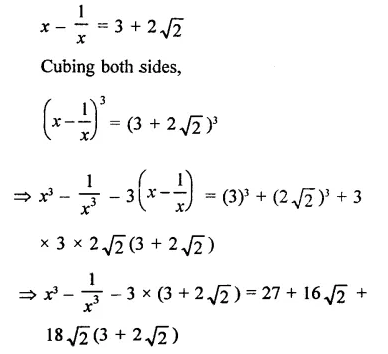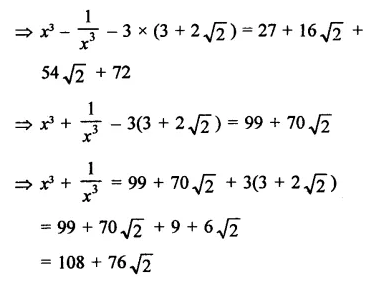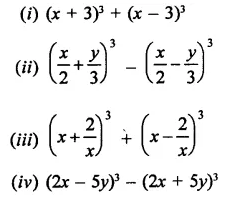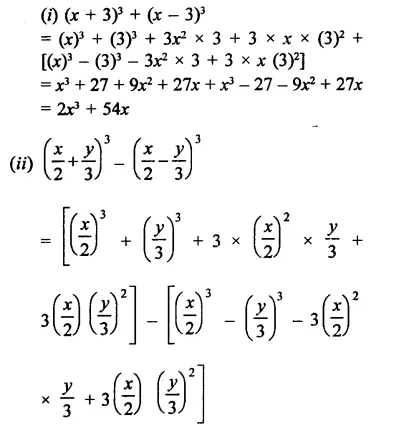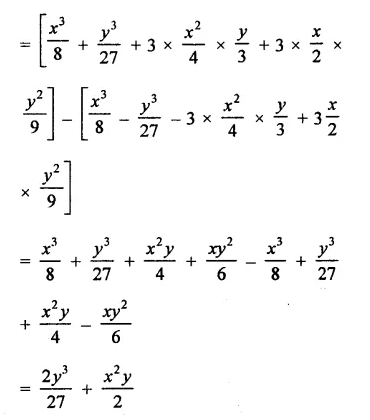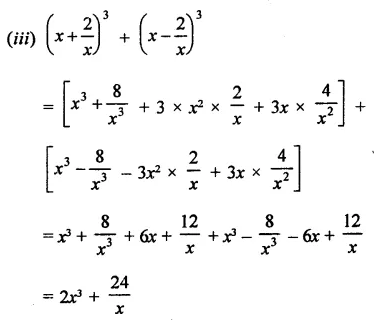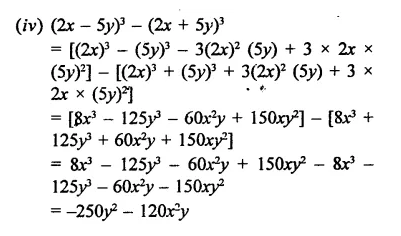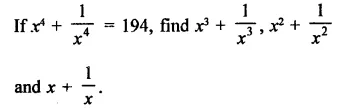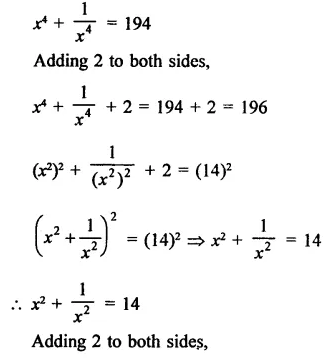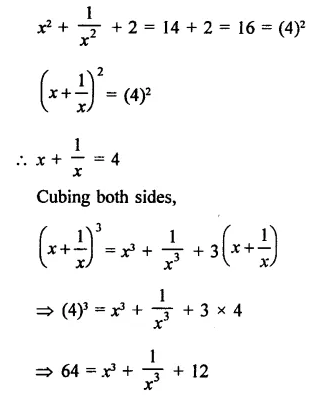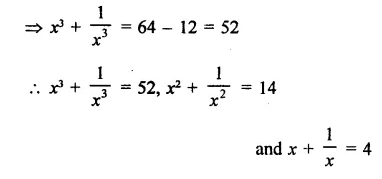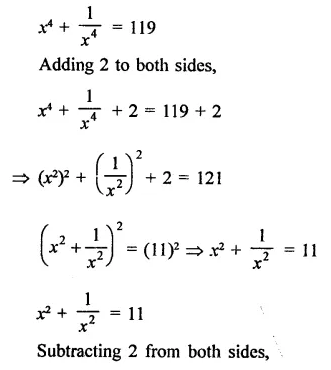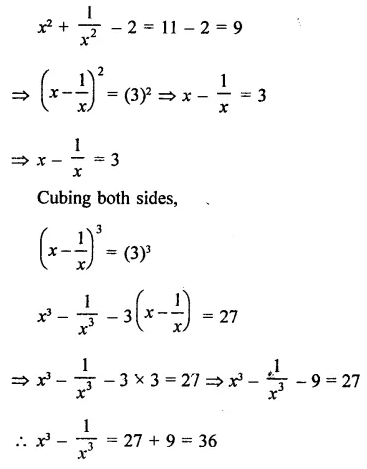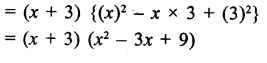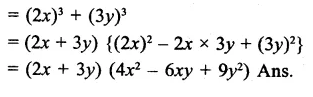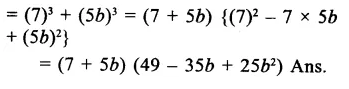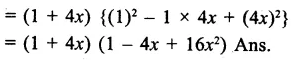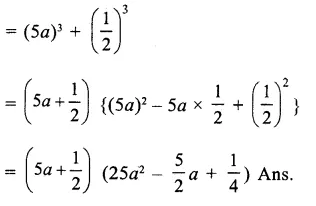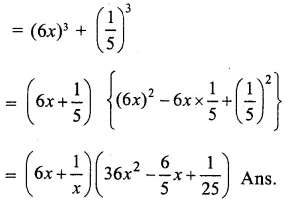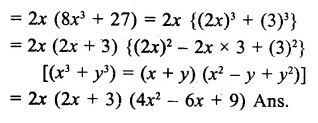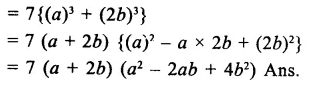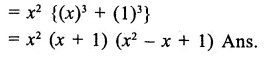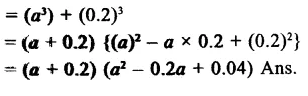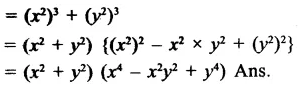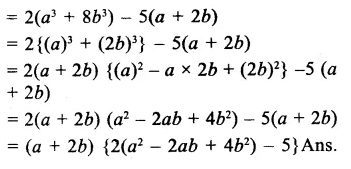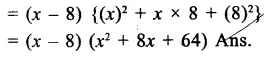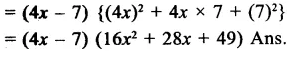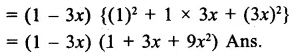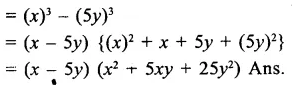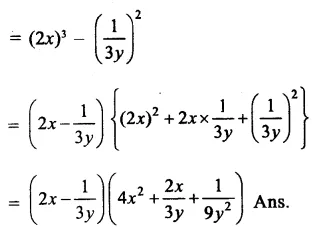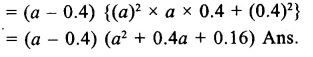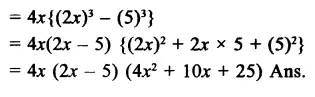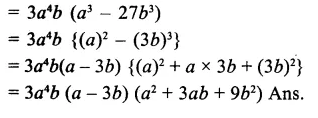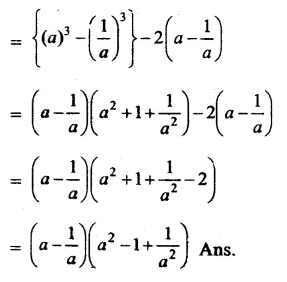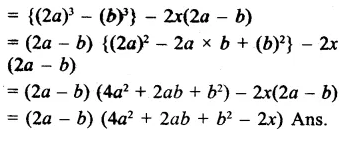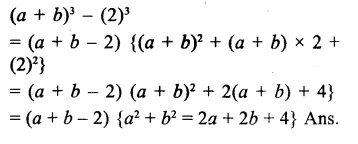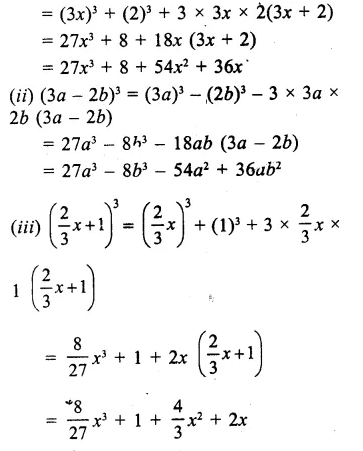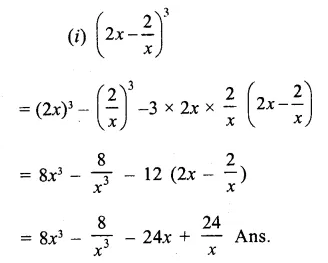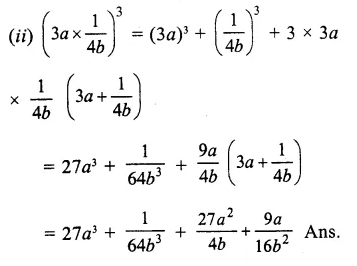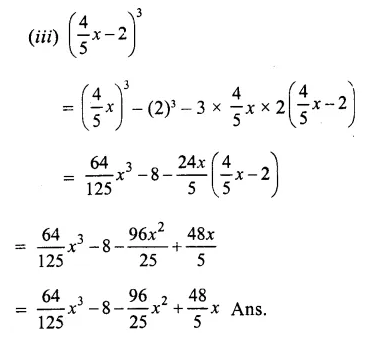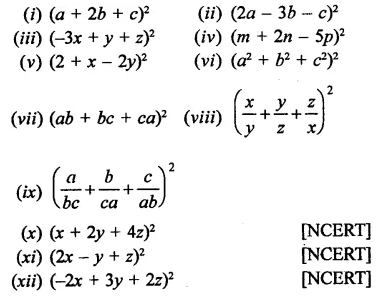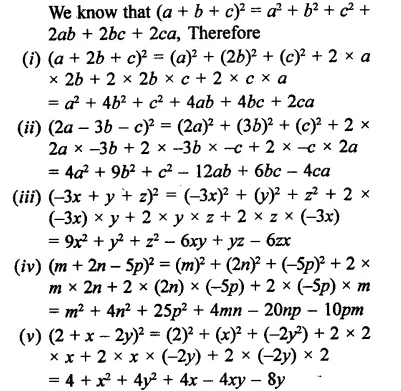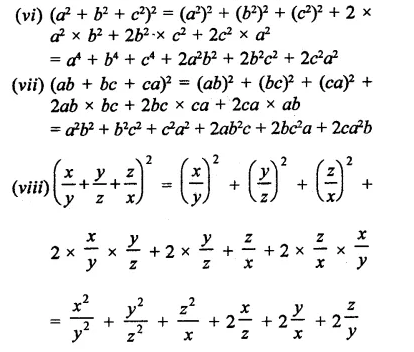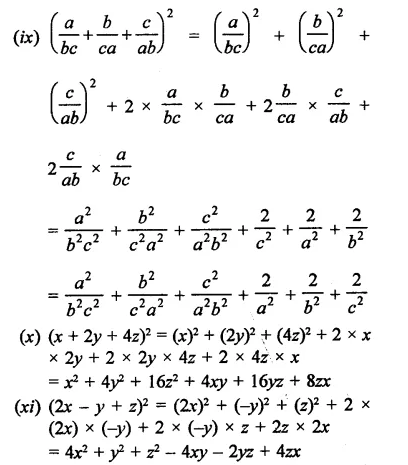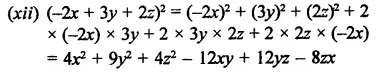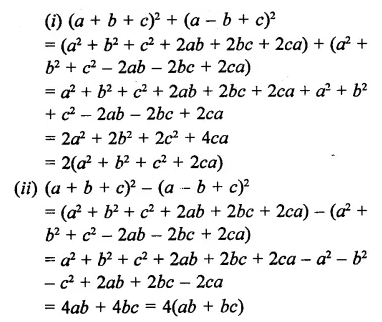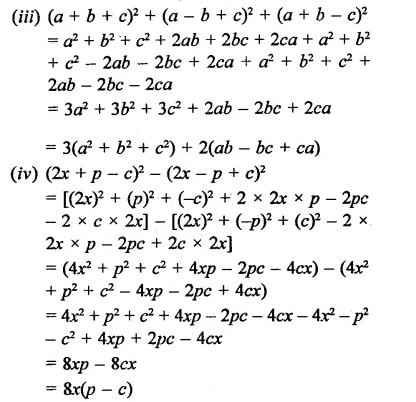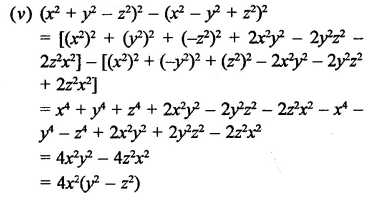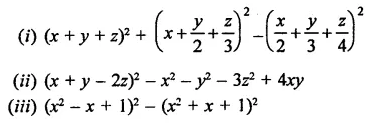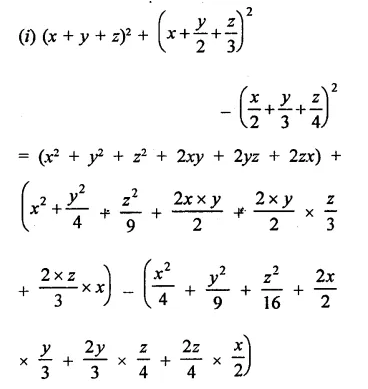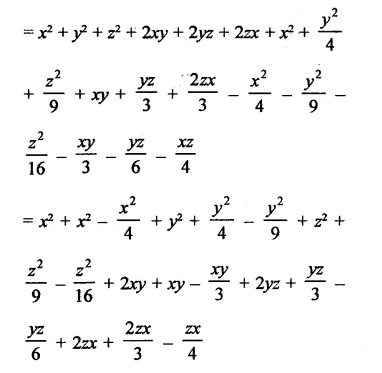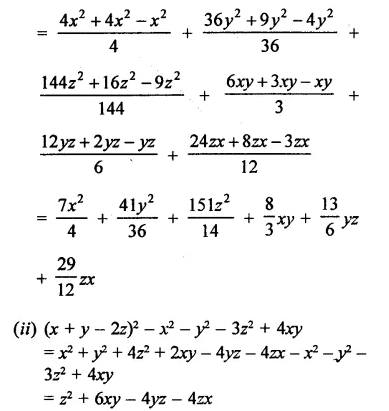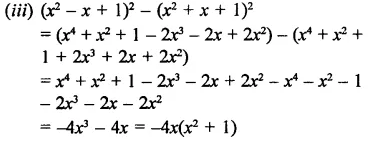CBSE Class 9

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4

Question 1.
Find the following products:
(i) (3x + 2y) (9X² – 6xy + Ay²)
(ii) (4x – 5y) (16x² + 20xy + 25y²)
(iii) (7p⁴ + q) (49p⁸ – 7p⁴q + q²)

Solution:

Question 2.
If x = 3 and y = -1, find the values of each of the following using in identity:

Solution:

Question 3.
If a + b = 10 and ab = 16, find the value of a² – ab + b² and a² + ab + b².
Solution:
a + b = 10, ab = 16 Squaring,
(a + b)² = (10)²
⇒ a² + b² + lab = 100
⇒ a² + b² + 2 x 16 = 100
⇒  a² + b² + 32 = 100
∴ a² + b² = 100 – 32 = 68
Now, a² – ab + b² = a² + b² – ab = 68 – 16 = 52
and a² + ab + b² = a² + b² + ab = 68 + 16 = 84

Question 4.
If a + b = 8 and ab = 6, find the value of a³ + b³.
Solution:
a + b = 8, ab = 6
Cubing both sides,
(a + b)³ = (8)3
⇒ a³ + b³ + 3 ab{a + b) = 512
⇒  a³ + b³ + 3 x 6 x 8 = 512
⇒  a³ + b³ + 144 = 512
⇒  a³ + b³ = 512 – 144 = 368
∴ a³ + b³ = 368

Question 5.
If a – b = 6 and ab = 20, find the value of a³-b³.
Solution:
a – b = 6, ab = 20
Cubing both sides,
(a – b)3 = (6)³
⇒  a³ – b³ – 3ab(a – b) = 216
⇒  a³ – b³ – 3 x 20 x 6 = 216
⇒  a³ – b³ – 360 = 216
⇒  a³ -b³ = 216 + 360 = 576
∴ a³ – b³ = 576

Question 6.
If x = -2 and y = 1, by using an identity find the value of the following:

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.3

Question 1.
Find the cube of each of the following binomial expressions:

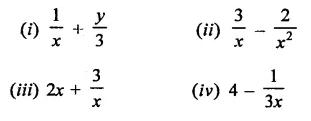
Solution:

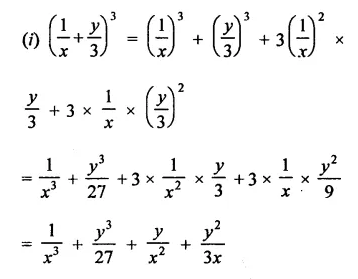
Question 2.
If a + b = 10 and ab = 21, find the value of a³ + b³.
Solution:
a + b = 10, ab = 21
Cubing both sides,
(a + b)³ = (10)³
⇒ a³ + 6³ + 3ab (a + b) = 1000
⇒  a³ + b³ + 3 x 21 x 10 = 1000
⇒  a³ + b³ + 630 = 1000
⇒  a³ + b³ = 1000 – 630 = 370
∴ a³ + b³ = 370

Question 3.
If a – b = 4 and ab = 21, find the value of a³-b³.
Solution:
a – b = 4, ab= 21
Cubing both sides,
⇒ (a – A)³ = (4)³
⇒ a³ – b³ – 3ab (a – b) = 64
⇒ a³-i³-3×21 x4 = 64
⇒  a³ – 6³ – 252 = 64
⇒  a³ – 6³ = 64 + 252 =316
∴ a³ – b³ = 316

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.
If 2x + 3y = 13 and xy = 6, find the value of 8x³ + 21y³.
Solution:
2x + 3y = 13, xy = 6
Cubing both sides,
(2x + 3y)³ = (13)³
⇒ (2x)³ + (3y)³ + 3 x 2x x 3X2x + 3y) = 2197
⇒ 8x³ + 27y³ + 18xy(2x + 3y) = 2197
⇒ 8x³ + 27y³ + 18 x 6 x 13 = 2197
⇒ 8X³ + 27y³ + 1404 = 2197
⇒  8x³ + 27y³ = 2197 – 1404 = 793
∴ 8x³ + 27y³ = 793

Question 10.
If 3x – 2y= 11 and xy = 12, find the value of 27x³ – 8y³.
Solution:
3x – 2y = 11 and xy = 12 Cubing both sides,
(3x – 2y)³ = (11)³
⇒  (3x)³ – (2y)³ – 3 x 3x x 2y(3x – 2y) =1331
⇒  27x³ – 8y³ – 18xy(3x -2y) =1331
⇒   27x³ – 8y³ – 18 x 12 x 11 = 1331
⇒  27x³ – 8y³ – 2376 = 1331
⇒  27X³ – 8y³ = 1331 + 2376 = 3707
∴ 2x³ – 8y³ = 3707

Question 11.
Evaluate each of the following:
(i)  (103)³
(ii) (98)³
(iii) (9.9)³
(iv) (10.4)³
(v) (598)³
(vi) (99)³
Solution:
We know that (a + bf = a³ + b³ + 3ab(a + b) and (a – b)³= a³ – b³ – 3 ab(a – b)
Therefore,
(i)  (103)³ = (100 + 3)³
= (100)³ + (3)³ + 3 x 100 x 3(100 + 3)    {∵ (a + b)³ = a³ + b³ + 3ab(a + b)}
= 1000000 + 27 + 900 x 103
= 1000000 + 27 + 92700
= 1092727
(ii) (98)³ = (100 – 2)³
= (100)³ – (2)³ – 3 x 100 x 2(100 – 2)
= 1000000 – 8 – 600 x 98
= 1000000 – 8 – 58800
= 1000000-58808
= 941192
(iii) (9.9)³ = (10 – 0.1)³
= (10)³ – (0.1)³ – 3 X 10 X 0.1(10 – 0.1)
= 1000 – 0.001 – 3 x 9.9
= 1000 – 0.001 – 29.7
= 1000 – 29.701
= 970.299
(iv) (10.4)³ = (10 + 0.4)³
= (10)³ + (0.4)³ + 3 x 10 x 0.4(10 + 0.4)
= 1000 + 0.064 + 12(10.4)
= 1000 + 0.064 + 124.8 = 1124.864
(v) (598)³ = (600 – 2)³
= (600)³ – (2)³ – 3 x 600 x 2 x (600 – 2)
= 216000000 – 8 – 3600 x 598
= 216000000 – 8 – 2152800
= 216000000 – 2152808
= 213847192
(vi) (99)³ = (100 – 1)³
= (100)³ – (1)³ – 3 x 100 x 1 x (100 – 1)
= 1000000 – 1 – 300 x 99
= 1000000 – 1 – 29700
= 1000000 – 29701
= 970299

Question 12.
Evaluate each of the following:
(i)  111³ – 89³
(ii) 46³ + 34³
(iii) 104³ + 96³
(iv) 93³ – 107³
Solution:
We know that a³ + b³ = (a + bf – 3ab(a + b) and a³ – b³ = (a – bf + 3 ab(a – b)
(i) 111³ – 89³
= (111 – 89)³ + 3 x ill x 89(111 – 89)
= (22)³ + 3 x 111 x 89 x 22
= 10648 + 652014 = 662662
(OR)
(a + b)³ – (a – b)³ = 2(b³ + 3a²b)
= 111³ – 89³ = (100 + 11)³ – (100 – 11)³
= 2(11³ + 3 x 100² x 11]
= 2(1331 + 330000]
= 331331 x 2 = 662662
(a + b)³ + (a- b)³ = 2(b³ + 3ab²)
(ii) 46³ + 34³ = (40 + 6)³ + (40 – 6)³
= 2[(40)³ + 3 x 40 x 6²]
= 2[64000 + 3 x 40 x 36]
= 2[64000 + 4320]
= 2 x 68320 = 136640
(iii) 104³ + 96³ = (100 + 4)³ + (100 – 96)³
= 2 [a³ + 3 ab²]
= 2[(100)³ + 3 x 100 x (4)²]
= 2[ 1000000 + 300 x 16]
= 2[ 1000000 + 4800]
= 1004800 x 2 = 2009600
(iv) 93³ – 107³ = -[(107)³ – (93)³]
= -[(100 + If – (100 – 7)³]
= -2[b³ + 3a²b)]
= -2[(7)³ + 3(100)² x 7]
= -2(343 + 3 x 10000 x 7]
= -2[343 + 210000]
= -2[210343] = -420686

Question 13.

Solution:

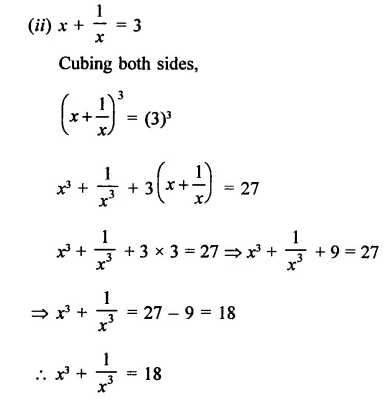
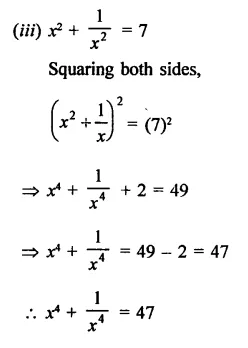
Question 14.
Find the value of 27X³ + 8y³ if
(i) 3x + 2y = 14 and xy = 8
(ii) 3x + 2y = 20 and xy = \(\frac { 14 }{ 9 }\)
Solution:

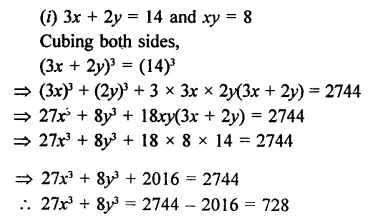
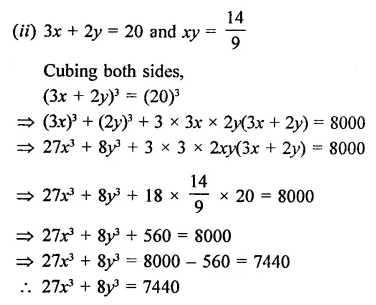
Question 15.
Find the value of 64x³ – 125z³, if 4x – 5z = 16 and xz = 12.
Solution:
4x – 5z = 16, xz = 12
Cubing both sides,
(4x – 5z)³ = (16)³
⇒ (4x)³ – (5y)³ – 3 x 4x x 5z(4x – 5z) = 4096
⇒ 64x³ – 125z³ – 3 x 4 x 5 x xz(4x – 5z) = 4096
⇒  64x³ – 125z³ – 60 x 12 x 16 = 4096
⇒ 64x³ – 125z³ – 11520 = 4096
⇒  64x³ – 125z³ = 4096 + 11520 = 15616

Question 16.

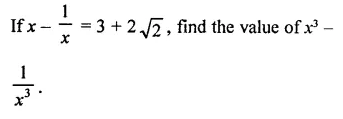
Solution:

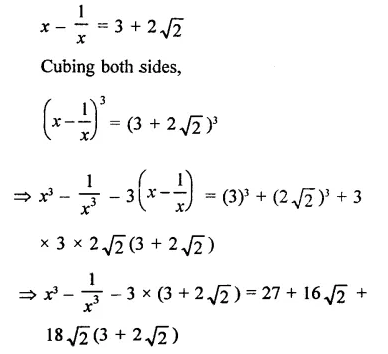
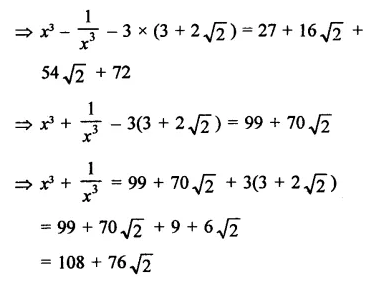
Question 17.
Simplify each of the following:

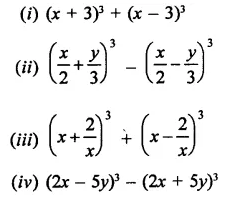
Solution:

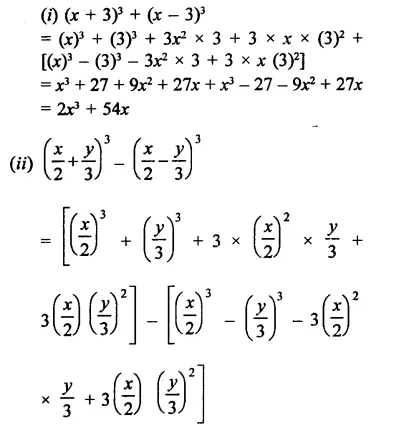
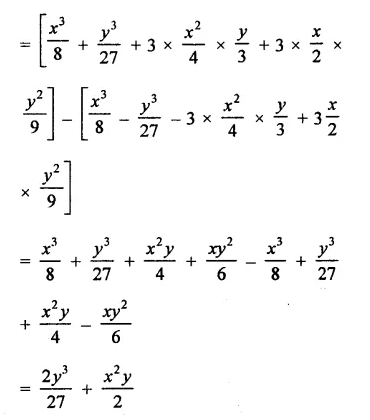
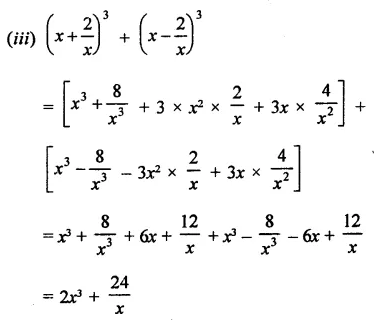
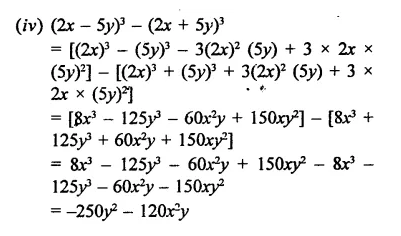
Question 18.

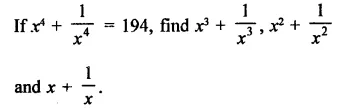
Solution:

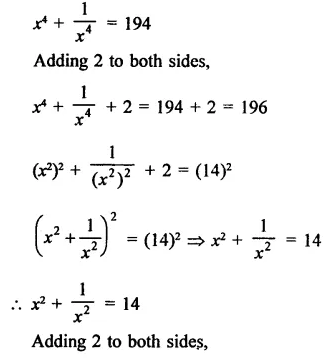
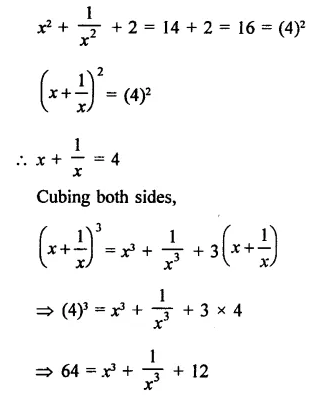
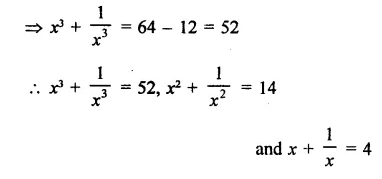
Question 19.

Solution:

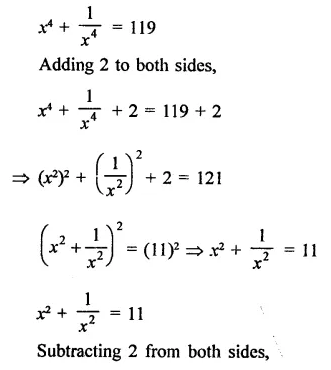
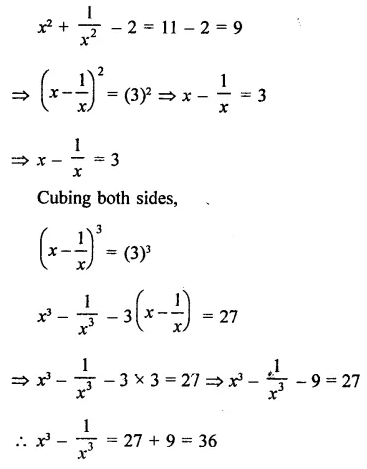
Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.2

Question 1.
Write the following in the expanded form:

Solution:

Question 2.
If a + b + c = 0 and a² + b² + c² = 16, find the value of ab + be + ca.
Solution:
a + b+ c = 0
Squaring both sides,
(a + b + c)² = 0
⇒ a² + b² + c² + 2(ab + bc + ca) = 0
16 + 2(ab + bc + c) = 0
⇒ 2(ab + bc + ca) = -16
⇒  ab + bc + ca =-\(\frac { 16 }{ 2 }\) = -8
∴ ab + bc + ca = -8

Question 3.
If a² + b² + c² = 16 and ab + bc + ca = 10, find the value of a + b + c.
Solution:
(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
= 16 + 2 x 10
= 16 + 20 = 36
= (±6)²
∴ a + b + c = ±6

Question 4.
If a + b + c = 9 and ab + bc + ca = 23, find the value of a² + b² + c².
Solution:
(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
⇒ (9)² = a² + b² + c² + 2 x 23
⇒ 81= a² + b² + c² + 46
⇒  a² + b² + c² = 81 – 46 = 35
∴ a² + b² + c² = 35

Question 5.
Find the value of 4x² + y² + 25z² + 4xy – 10yz – 20zx when x = 4, y = 3 and z = 2.
Solution:
x = 4, y – 3, z = 2
⇒ 4x² + y² + 25z² + 4xy – 10yz – 20zx
= (2x)² + (y)² + (5z)² + 2 x2 x x y-2 x y x 5z – 2 x 5z x 2x
= (2x + y- 5z)²
= (2 x 4 + 3- 5 x 2)²
= (8 + 3- 10)²
= (11 – 10)²
= (1)² = 1

Question 6.
Simplify:
(i)  (a + b + c)² + (a – b + c)²
(ii) (a + b + c)² –  (a – b + c)²
(iii) (a + b + c)² +   (a – b + c)² + (a + b – c)²
(iv) (2x + p – c)² – (2x – p + c)²
(v) (x² + y² – z²)² – (x² – y² + z²)²
Solution:

Question 7.
Simplify each of the following expressions:

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.