CBSE Class 9

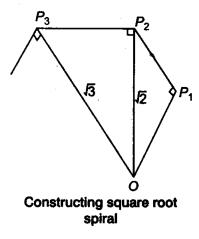
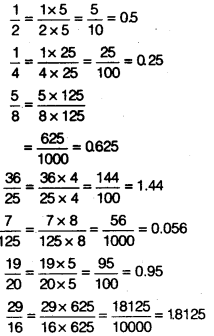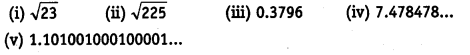NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5

Question 1.
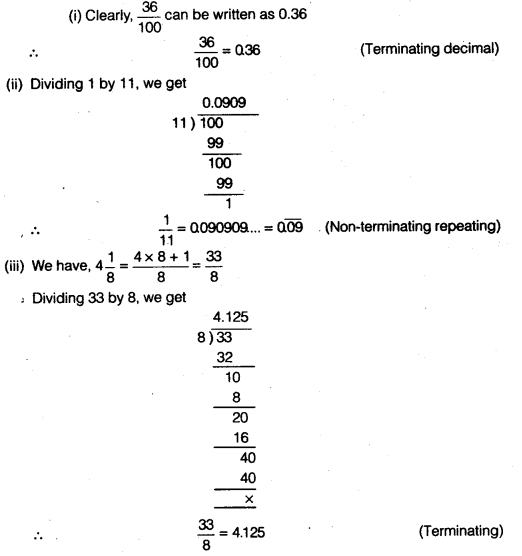
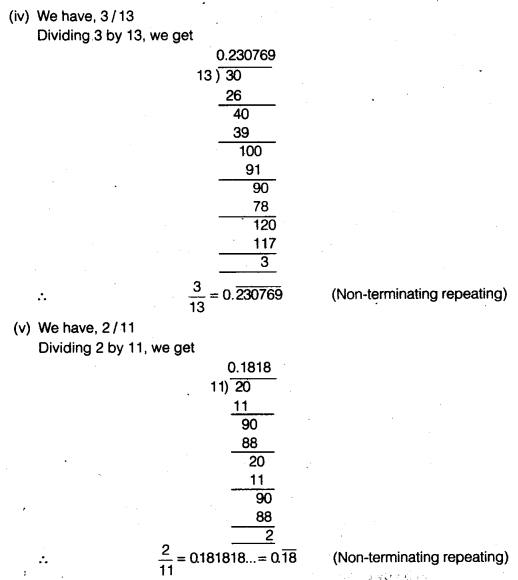
Classify the following numbers as rational or irrational.

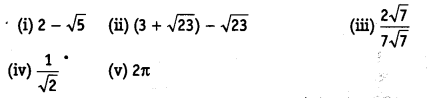
Solution:
(i) Irrational ∵ 2 is a rational number and √5 is an irrational number.
∴ 2.√5 is an irrational number.
(∵The difference of a rational number and an irrational number is irrational)
(ii) 3 + \( \sqrt{23} \) – \( \sqrt{23} \) = 3 (rational)
(iii) \(\frac { 2\sqrt { 7 } }{ 7\sqrt { 7 } }\) (rational)
(iv) \(\frac { 1 }{ \sqrt { 2 } }\)(irrational) ∵ 1 ≠ 0 is a rational number and \( \sqrt{2} \)≠ 0 is an irrational number.
∴ \(\frac { 1 }{ \sqrt { 2 } }\) is an irrational number. 42
(∵ The quotient of a non-zero rational number with an irrational number is irrational).
(v) 2π (irrational) ∵ 2 is a rational number and π is an irrational number.
∴ 2x is an irrational number. ( ∵The product of a non-zero rational number with an irrational number is an irrational)

Question 2.
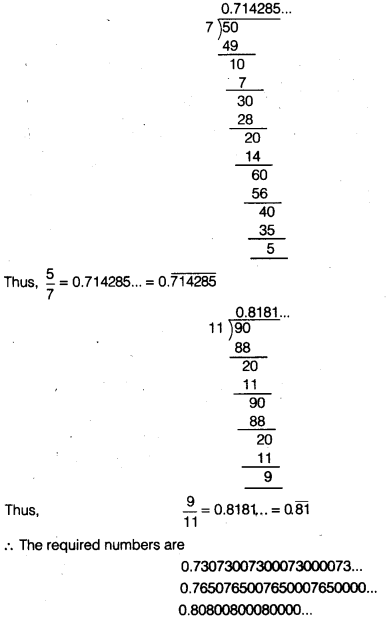
Simplify each of the following expressions

Solution:

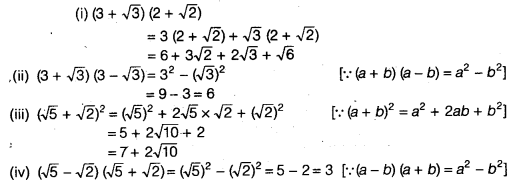
Question 3.
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π = \(\frac { c }{ d }\). This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Solution:
Actually \(\frac { c }{ d }\) = \(\frac { 22 }{ 7 }\),which is an approximate value of π.

Question 4.
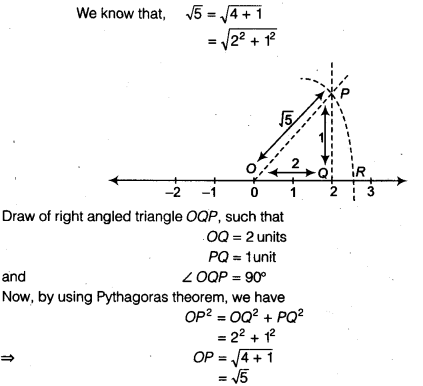
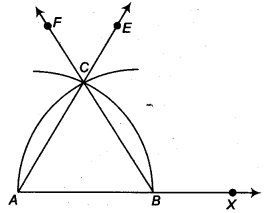
Represent \( \sqrt{9.3} \) on the number line.
Solution:
Firstly we draw AB = 9.3 units. Now, from S, mark a distance of 1 unit. Let this point be C. Let O be the mid-point of AC. Now, draw aemi – circle with centre O and radius OA. Let us draw a line perpendicular to AC passing through point B and intersecting the semi-circle at point D.

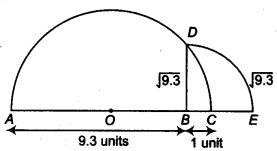
∴ The distance BD = \( \sqrt{9.3} \)
Draw an arc with centre B and radius BD, which intersects the number line at point E, then the point E represents \( \sqrt{9.3} \) .

Question 5.
Rationalise the denominator of the following

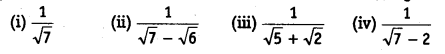
Solution:

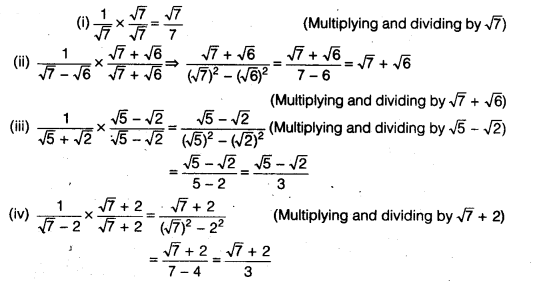
We hope the NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4

Question 1.
Visualise 3.765 on the number line, using successive magnification.
Solution:
We know that, 3.765 lies between 3 and 4. So, let us divide the part of the number line between 3 and 4 into 10 equal parts and look at the portion between 3.7 and 3.8 through a magnifying glass. Now 3.765 lies between 3.7 and 3.8 [Fig. (i)]. Now, we imagine to divide this again into ten equal parts. The first mark will represent 3.71, the next 3.72 and soon. To see this clearly,we magnify this as shown in [Fig. (ii)].

Again 3.765 lies between 3.76 and 3.77 [Fig. (ii)]. So, let us focus on this portion of the number line [Fig. (iii)] and imagine to divide it again into ten equal parts [Fig. (iii)]. Here, we can visualise that 3.761 is the first mark and 3.765 is the 5th mark .in these subdivisions. We call this process of visualisation of representation of numbers on the number line through a magnifying glass as the process of successive magnification.

So, we get seen that it is possible by sufficient successive magnifications of visualise the position (or representation) of a real number with a terminating decimal expansion on the number line.

Question 2.
Visualise 4.\(\bar { 26 }\) on the number line, upto 4 decimal places.
Solution:
We adopt process by successive magnification and successively decreasethe lengths of the portion of the number line in which 4.\(\bar { 26 }\) is located. Since 4.\(\bar { 26 }\) is located between 4 and 5 and is divided into 10 equal parts [Fig. (i)]. In further, we locate 4.26between 4.2 and 4.3 [Fig. (ii)].

To get more accurate visualisation of the representation, we divide this portion into 10 equal parts and use a magnifying glass to visualise that 4.\(\bar { 26 }\) lies between 4.26 and 4.27. To visualise 4.\(\bar { 26 }\) more clearly we divide again between 4.26 and 4.27 into 10 equal parts and visualise the repsentation of 4.\(\bar { 26 }\) between 4.262 and 4.263 [Fig. (iii)].

Now, for a much better visualisation between 4.262 and 4.263 is agin divided into 10 equal parts [Fig. (iv)]. Notice that 4.\(\bar { 26 }\) is located closer to 4.263 then to 4.262 at 4.2627.

Remark: We can adopt the process endlessly in this manner and simultaneously imagining the decrease in the length of the number line in which 4.\(\bar { 26 }\) is located.

We hope the NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3

Question 1.
Write the following in decimal form and say what kind of decimal expansion each has

Solution:

Question 2.
You know that \(\frac { 1 }{ 7 }\) = \(\bar { 0.142857 }\). Can you predict what the decimal expansions of \(\frac { 2 }{ 7 }\) , \(\frac { 13 }{ 7 }\) , \(\frac { 4 }{ 7 }\) , \(\frac { 5 }{ 7 }\) , \(\frac { 6 }{ 7 }\) are , without actually doing the long division? If so, how?
Solution:

Question 3.
Express the following in the form \(\frac { p }{ q }\)where p and q are integers and q ≠ 0.
(i) 0.\(\bar { 6 }\)
(ii) 0.4\(\bar { 7 }\)
(iii) 0.\(\overline { 001 }\)
Solution:
(i)Let x= 0.\(\bar { 6 }\) = 0.666… ….(i)
Multiplying Eq. (i) by 10, we get
10x = 6.666.. ….(ii)
On subtracting Eq. (ii) from Eq. (i), we get
(10x- x)=(6.666…) – (0.666…)
9x = 6
x= 6/9
⇒ x=2/3

(ii) Let x = 0.4\(\bar { 7 }\) = 0.4777… …(iii)
Multiplying Eq. (iii) by 10. we get
10x = 4.777… . …(iv)
Multiptying Eq. (iv) by 10, we get
100x = 47.777 ….. (v)
On subtracting Eq. (v) from Eq. (iv), we get
(100 x – 10x)=(47.777….)-(4.777…)
90x =43
⇒ x = \(\frac { 43 }{ 90 }\)

(iii) Let x = 0.\(\overline { 001 }\)= 0.001001001… …(vI)
Multiplying Eq. (vi) by (1000), we get
1000x = 1.001001001… .. .(vii)
On subtracting Eq. (vii) by Eq. (vi), we get
(1000x—x)=(1.001001001….) – (0.001001001……)
999x = 1
⇒ x = \(\frac { 1 }{ 999 }\)

Question 4.
Express 0.99999… in the form \(\frac { p }{ q }\)Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Let x = 0.99999… ………..(i)
Multiplying Eq. (i) by 10, we get
10x = 9.99999… …(ii)
On subtracting Eq. (ii) by Eq. (i), we get
(10 x – x) = (9.99999..) – (0.99999…)
9x = 9
⇒ x = \(\frac { 9 }{ 9 }\)
x = 1

Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac { 1 }{ 17 }\)? Perform the division to check your answer.
Solution:
The maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac { 1 }{ 17 }\) is 17-1 = 16 we have,

Thus,\(\frac { 1 }{ 17 }\) = 0.\(\overline { 0588235294117647….., }\)a block of 16-digits is repeated.

Question 6.
Look at several examples of rational numbers in the form \(\frac { p }{ q }\) (q≠ 0). Where, p and q are integers with no common factors other that 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Consider many rational numbers in the form \(\frac { p }{ q }\) (q≠ 0). where p and q are integers with no common factors other that 1 and having terminating decimal representations.
Let the various such rational numbers be \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 4 }\), \(\frac { 5 }{ 8 }\), \(\frac { 36 }{ 25 }\), \(\frac { 7 }{ 125 }\), \(\frac { 19 }{ 20 }\), \(\frac { 29 }{ 16 }\) etc.
In all cases, we think of the natural number which when multiplied by their respective denominators gives 10 or a power of 10.

From the above, we find that the decimal expansion of above numbers are terminating. Along with we see that the denominator of above numbers are in the form 2m x 5n, where m and n are natural numbers. So, the decimal representation of rational numbers can be represented as a terminating decimal.

Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
0.74074007400074000074…
0.6650665006650006650000…
0.70700700070000…

Question 8.
Find three different irrational numbers between the rational numbers \(\frac { 5 }{ 7 }\) and \(\frac { 9 }{ 11 }\) .
Solution:
To find irrational numbers, firstly we shall divide 5 by 7 and 9 by 11,
so,

Question 9.
Classify the following numbers as rational or irrational

Solution:
(i) \( \sqrt{23} \) (irrational ∵ it is not a perfect square.)
(ii) \( \sqrt{225} \) = 15 (rational) (whole number.)
(iii) 0.3796 = rational (terminating.)
(iv) 7.478478… =7.\(\bar { 478 }\) = rational (non-terminating repeating.)
(v) 1.101001000100001… = irrational (non-terminating non-repeating.)

We hope the NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2

Question 1.
State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m , where m is a natural number.
(iii) Every real number is an irrational number.
Solution:
(i) True (∵ Real numbers = Rational numbers + Irrational numbers.)
(ii) False (∵ no negative number can be the square root of any natural number.)
(iii) False (∵ rational numbers are also present in the set of real numbers.)

Question 2.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution:
No, the square roots of all positive integers are not irrational.
e.g., √l6 = 4
Here, ‘4’ is a rational number.

Question 3.
Show how √5 can be represented on the number line.
Solution:

Now, take O as centre OP = √5 as radius, draw an arc, which intersects the line at point R. .
Hence, the point R represents √5.

Question 4.
Classroom activity (constructing the ‘square root spiral’).
Solution:
Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁, of unit lengths Draw a line segment P₁, P₂ perpendicular to OP₁ of unit length (see figure).

Now, draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n-1 P_n by drawing a line segment of unit length perpendicular to
OP_n-1. In this manner, you will have created the points P₂, P₃,…… P_n,….. and
joined them to create a beautiful spiral depicting √2,√3,√4,……

We hope the NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.2, drop a comment below and we will get back to you at the earliest.