NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 12 |
| Chapter Name | Constructions |
| Exercise | Ex 12.1 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction
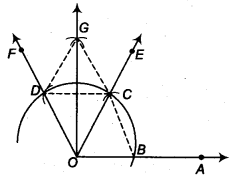
- Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
- Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
- Draw the ray OE passing through C.
Then, ∠EOA = 60° - Draw the ray of passing through D. Then, ∠FOE = 60°.
- Next, taking Cand Das centres and with the radius more than \(\frac { 1 }{ 2 }\) CD, draw arcs to intersect each other, say at G.
- Draw the ray OG. This ray OG is the bisector of the ∠FOE i.e.,
∠FOG = ∠EOG = \(\frac { 1 }{ 2 }\) ∠FOE = \(\frac { 1 }{ 2 }\) (60°) = 30°
Thus, ∠GOA = ∠GOE + ∠EOA
= 30° + 60° = 90°
Justification
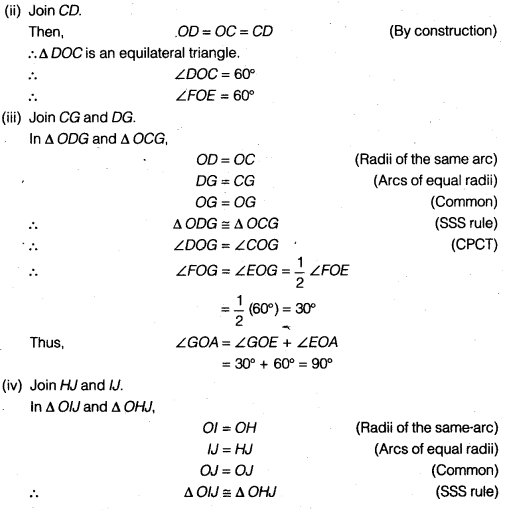
(i) Join BC.
Then, OC=OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°
∴ ∠EOA = 60°
(ii) Join CD.
Then, OD=OC=CD (By construction)
∴ ∆DOC is an equilateral triangle.
∴ ∠DOC = 60°
∴ ∠FOE = 60°
(iii) Join CG and DG.
In ∆ODG and ∆OCG,
OD = OC (Radii of the same arc)
DG = CG (Arcs of equal radii)
OG = OG (Common)
∴ ∆ ODG ≅ ∆OCG (SSS rule)
∴ ∠DOG = ∠COG (CPCT)
∴ ∠FOG = ∠EOG = \(\frac { 1 }{ 2 }\) ∠FOE
= \(\frac { 1 }{ 2 }\) (60°) = 30°
Thus, ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°
Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction
- Taking O as centre and some radius, draw an arc of a circle which intersects OA, say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
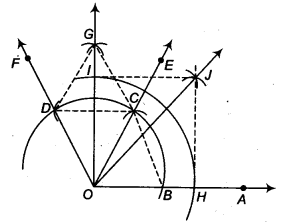
- Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
- Draw the ray OE passing through C. Then, ∠EOA = 60°.
- Draw the ray OF passing through D. Then, ∠FOE = 60°.
- Next, taking C and D as centres and with radius more than \(\frac { 1 }{ 2 }\) CD, draw arcs to intersect each other, say at G.
- Draw the ray OG. This ray OG is the bisector of the ∠FOE,
i.e., ∠FOG = ∠EOG = \(\frac { 1 }{ 2 }\) ∠FOE = \(\frac { 1 }{ 2 }\) (60°) = 30°.
thus , ∠GOA = ∠GOE + ∠EOA
= 30° + 60° = 90° - Now taking O as centre and any radius, draw an arc to intersect the rays OA and OG, say at Hand /, respectively.
- Next, taking H and las centres and with the radius more than \(\frac { 1 }{ 2 }\) Hl, draw
arcs to intersect each other, say at J. - Draw the ray OJ. This ray OJ is the required bisector of the ∠GOA.
∠GOJ = ∠AOJ = \(\frac { 1 }{ 2 }\) ∠GOA
= \(\frac { 1 }{ 2 }\) (90°) = 45°
Justification
(i) Join BC. (By construction)
Then, OC = OB = BC
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°
∴ ∠EOA = 60°
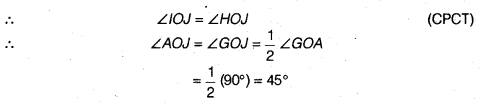
Question 3.
Construct the angles of the following measurements
(i) 30°
(ii) 22 \(\frac { 1 }{ 2 }\)
(iii) 15°
Solution:
(i) Steps of construction
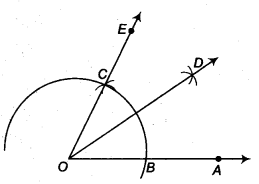
- Taking O as centre and some radius, draw an arc of a circle which intersects OA, say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
- Draw the ray OE passing through C. Then, ∠EOA = 60°.
- Taking B and C as centres and with the radius more than \(\frac { 1 }{ 2 }\) BC, draw arcs to intersect each other, say at D.
- Draw the ray OD, this ray OD is the bisector of the ∠EOA, i.e.,
∠EOD = ∠AOD = \(\frac { 1 }{ 2 }\) ∠EOA = \(\frac { 1 }{ 2 }\) (60°) = 30°
(ii) Steps of construction
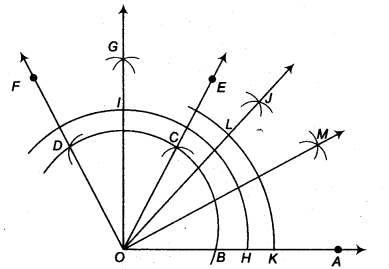
- Taking O as centre and some radius, draw an arc of a circle which, intersects OA, say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
- Taking C as centre and with the same radius as before, drawn an arc intersecting the arc drawn in step 1, say at D.
- Draw the ray OE passing through C. Then, ∠EOA = 60°.
- Draw the ray OF passing through D. Then, ∠FOE = 60°.
- Next, taking C and D as centres and with radius more than \(\frac { 1 }{ 2 }\)CD, draw arcs to intersect each other, say at G.
- Draw the ray OG. This ray OG is the bisector of the ∠FOE,
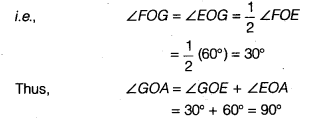
- Now, taking O as centre and any radius, draw an arc to intersect the rays OA and OG, say at H and l, respectively.
- Next, taking H and l as centres and with the radius more than \(\frac { 1 }{ 2 }\)Hl, draw arcs to intersect each other, say at J.
- Draw the ray OJ. This ray OJ is the bisector of the ∠GOA
i. e., ∠GOJ = ∠AOJ = \(\frac { 1 }{ 2 }\) ∠GOA
= \(\frac { 1 }{ 2 }\) (90°) = 45 ° - Now, taking O as centre and any radius, drawn an arc to intersect the rays OA and OJ, say at K and L, respectively.
- Next, taking K and L as centres and with the radius more than \(\frac { 1 }{ 2 }\)KL, draw arcs to intersect each other, say at H.
- Draw the ray OM. This ray OM is the bisector of the ∠AOJ, i.e., ∠JOM = ∠AOM
= \(\frac { 1 }{ 2 }\) ∠AOJ = \(\frac { 1 }{ 2 }\) (45°) = 22 \(\frac { 1 }{ 2 }\) °
(iii) Steps of construction
- Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C..
- Draw the ray OE passing through C. Then, ∠EOA = 60°.
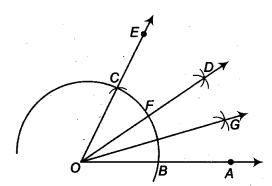
- Now, taking 6 and Cas centres and with the radius more than \(\frac { 1 }{ 2 }\) BC, draw arcs to intersect each other, say at D.
- Draw the ray OD intersecting the arc drawn in step 1 at F. This ray OD is the bisector of the ∠EOA, i.e.,
∠EOD = ∠AOD = \(\frac { 1 }{ 2 }\) ∠EOA = \(\frac { 1 }{ 2 }\) (60°) = 30° - Now, taking B and F as centres and with the radius more than \(\frac { 1 }{ 2 }\) BF, draw arcs to intersect each other, say at G.
- Draw the ray OG. This ray OG is the bisector of the ∠AOD,
i. e., ∠DOG = ∠AOG = \(\frac { 1 }{ 2 }\) ∠AOD = \(\frac { 1 }{ 2 }\) (30°) = 15°
- Draw the ray OG. This ray OG is the bisector of the ∠AOD,
Question 4.
Construct the following angles and verify by measuring them by a protractor
(i) 75°
(ii) 105°
(iii) 135°
Solution:
(i) Steps of construction
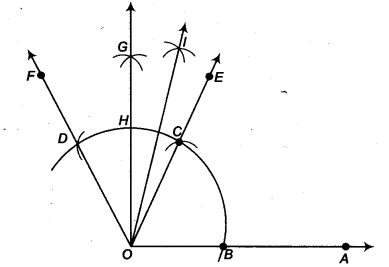
- Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
- Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
- Join the ray OE passing through C. Then, ∠EOA = 60°.
- Draw the ray of passing through D. Then, ∠FOE = 60°.
- Next, taking C and D as centres and with the radius more than \(\frac { 1 }{ 2 }\)CD, draw arcs to intersect each other, say at G.
- Draw the ray OG intersecting the arc of step 1 at H. This ray OG is the bisector of the ∠FOE, i.e., ∠FOG = ∠EOG
= \(\frac { 1 }{ 2 }\) ∠FOE = \(\frac { 1 }{ 2 }\)(60°) = 30° - Next, taking Cand H as centres and with the radius more than \(\frac { 1 }{ 2 }\)CH, draw
arcs to intersect each other, say at l.
Draw the ray OI. This ray OI is the bisector of the ∠GOE,
i. e., ∠GOI = ∠EOI = \(\frac { 1 }{ 2 }\) ∠GOE = \(\frac { 1 }{ 2 }\) (30°) = 15°
Thus, ∠IOA = ∠IOE + ∠EOA
=15°+ 60° = 75°
On measuring the ∠IOA by protractor, we find that ∠IOA = 15°
Thus, the construction is verified.
(ii) Steps of construction
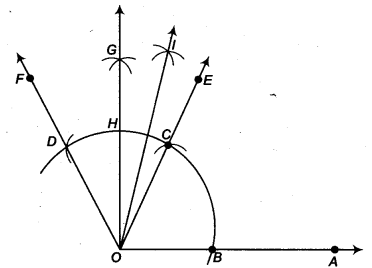
- Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
- Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at a point D.
- Draw the ray Of passing through C. Then, ∠EOA = 60°.
- Draw the ray OF passing through D. Then, ∠FOE = 60°.
- Next, taking Cand Das centres and with the radius more than \(\frac { 1 }{ 2 }\) CD, draw arcs to intersect each other, say at G.
- Draw the ray OG intersecting the arc drawn in step 1 at H. This ray OG is the bisector of the ∠FOE, i.e.,
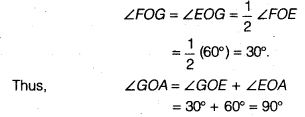
- Next, taking H and D as centres and with the radius more than \(\frac { 1 }{ 2 }\) HD, draw arcs to intersect each other, say at l.
- Draw the ray Ol. This ray Ol is the bisector of the ∠FOG, i.e.,
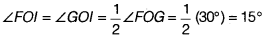
Thus, ∠lOA = ∠IOG + ∠GOA = 15° + 90° = 105°. On measuring the ∠lOA by protractor, we find that ∠FOA = 105°.
Thus, the construction is verified.
(iii) Steps of construction
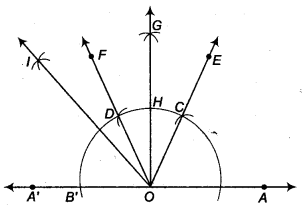
- Produce AO to A’ to form ray OA’.
- Taking O as centre and some radius, draw an arc of a circle which intersects OA at a point B and OA’ at a point B’.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C.
- Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
- Draw the ray OE passing through C, then ∠EOA = 60°.
- Draw the ray OF passing through D, then ∠FOE = 60°.
- Next, taking C and D as centres and with the radius more than \(\frac { 1 }{ 2 }\) CD, draw arcs to intersect each other, say at G.
- Draw the ray OGintersecting the arc drawn in step 1 at H. This ray OG is the bisector of the ∠FOE i,e.,
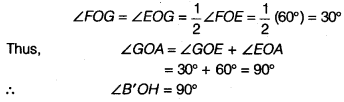
- Next, taking B’ and H as centres and with the radius more than \(\frac { 1 }{ 2 }\) B’H, drawn arcs to intersect each other, say at l.
- Draw the ray Ol. This ray Ol is the bisector of the ∠B’OG i.e.,
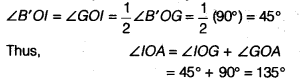
On measuring the ∠IOA by protractor, we find that ∠lOA = 135°.
Thus, the construction is verified.
Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
Steps of construction
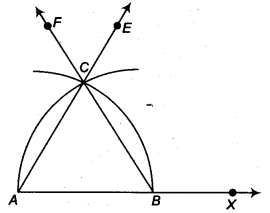
- Take a ray AX with initial point A From AX, cut off AB = 4 cm.
- Taking A as centre and radius (= 4 cm), draw an arc of a circle, which intersects AX, say at a point B.
- Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
- Draw the ray AE passing through C.
- Next, taking B as centre and radius (= 4 cm), draw an arc of a circle, which intersects AX, say at a point A
- Taking A as centre and with the same radius as in step 5, draw an arc intersecting the previously drawn arc, say at a point C.
Draw the ray BF passing through C.
Then, ∆ ABC is the required triangle with gives side 4 cm.
Justification
AB = BC (By construction)
AB = AC (By construction)
∴ AB = BC = CA
∴ ∆ ABC is an equilateral triangle.
∴ The construction is justified.
We hope the NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.1, drop a comment below and we will get back to you at the earliest.