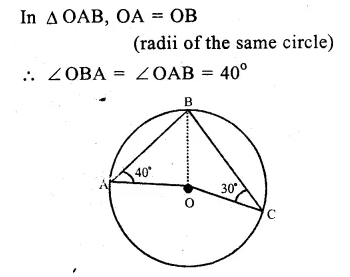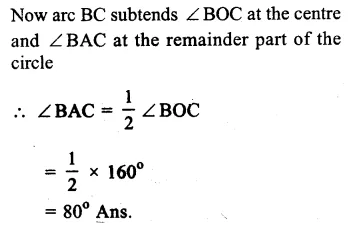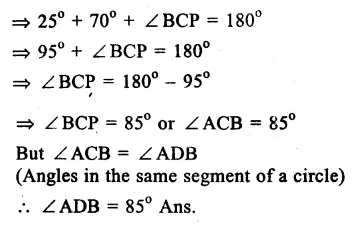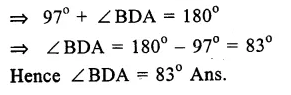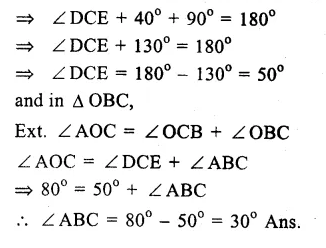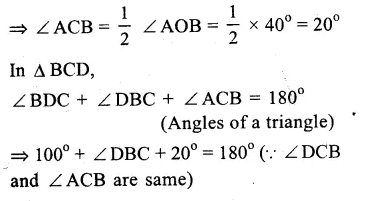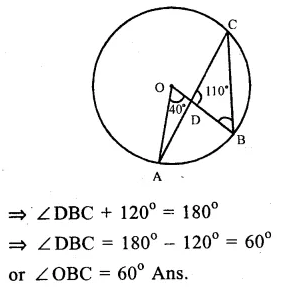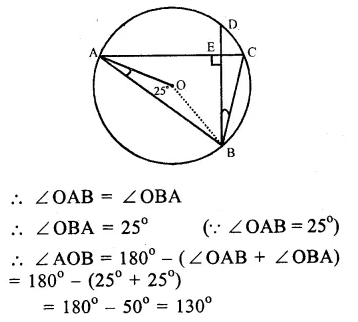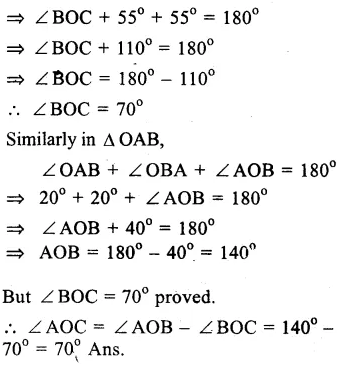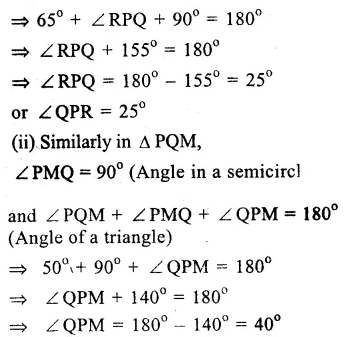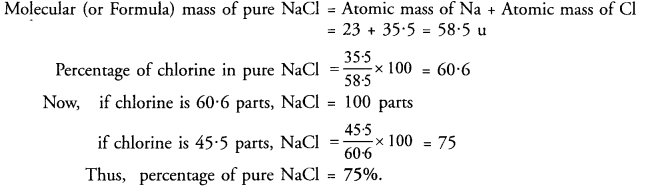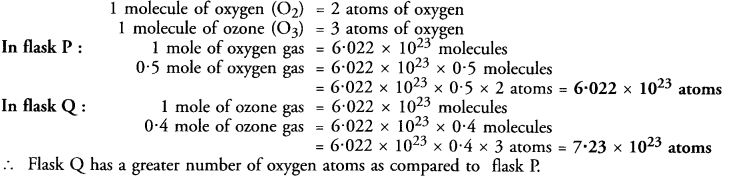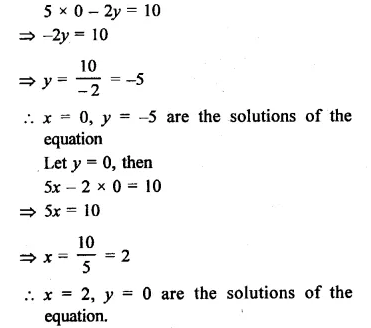CBSE Class 9

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C

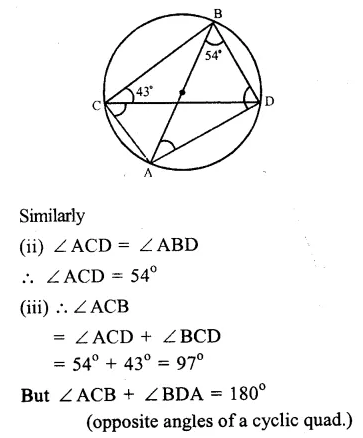
Question 1.
Solution:
In cyclic quad. ABCD, ∠ DBC = 60° and ∠BAC = 40°
∴∠ CAD and ∠ CBD are in the same segment of the circle.
∴∠ CAD = ∠ CBD or ∠ DBC
=> ∠ CAD = 60°
∴∠BAD = ∠BAC + ∠CAD
= 40° + 60° = 100°
But in cyclic quad. ABCD,
∠BAD + ∠BCD = 180°
(Sum of opposite angles)
=> 100° + ∠BCD = 180°
=> ∠BCD = 180° – 100°
∴ ∠ BCD = 80°
Hence (i) ∠BCD = 80° and
(ii) ∠CAD = 60° Ans.

Question 2.
Solution:
In the figure, POQ is diameter, PQRS is a cyclic quad, and ∠ PSR =150° In cyclic quad. PQRS.
∠ PSR + ∠PQR = 180°
(Sum of opposite angles)
=> 150° + ∠PQR = 180°
=> ∠PQR = 180°- 150° = 30°
=> ∠PQR =180° – 150° = 30°
Now in ∆ PQR,
∴∠ PRQ = 90° (Angle in a semicircle)
∴∠ RPQ + ∠PQR = 90°
=> ∠RPQ + 30° = 90°
=> ∠RPQ = 90° – 30° = 60° Ans.

Question 3.
Solution:
In cyclic quad. ABCD,
AB || DC and ∠BAD = 100°
∠ ADC = ∠BAD =180°
(co-interior angles)

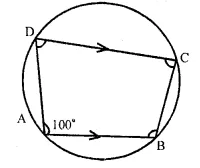
=> ∠ ADC + 100° = 180°
=> ∠ADC = 180° – 100° = 80°
∴ ABCD is a cyclic quadrilateral.
∴ ∠BAD + ∠BCD = 180°
=> 100° + ∠ BCD = 180°
=> ∠BCD = 180° – 100°
=> ∠BCD = 80°
Similarly ∠ABC + ∠ADC = 180°
=> ∠ABC + 80° = 180°
=> ∠ABC = 180° – 80° = 100°
Hence (i) ∠BCD = 80° (ii) ∠ADC = 80° and (iii) ∠ABC = 100° Ans.

Question 4.
Solution:
O is the centre of the circle and arc ABC subtends an angle of 130° at the centre i.e. ∠AOC = 130°. AB is produced to P
Reflex ∠AOC = 360° – 130° = 230°
Now, arc AC subtends reflex ∠ AOC at the centre and ∠ ABC at the remaining out of the circle.

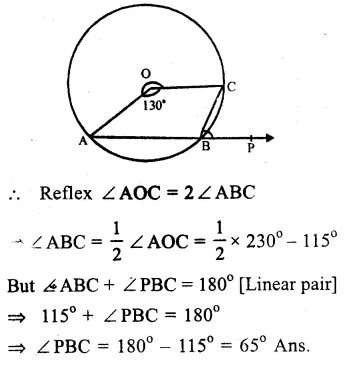
Question 5.
Solution:
In the figure, ABCD is a cyclic quadrilateral in which BA is produced to F and AE is drawn parallel to CD.
∠ABC = 92° and ∠FAE = 20°
ABCD is a cyclic quadrilateral.

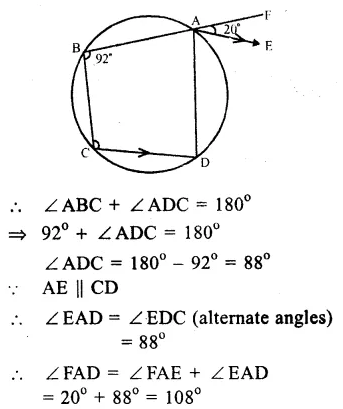
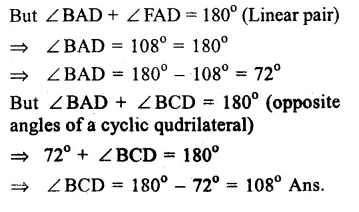
Question 6.
Solution:
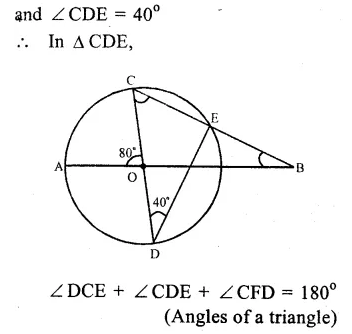
In the figure, BD = DC and ∠CBD = 30°
In ∆ BCD,
BD = DC (given)
∠ BCD = ∠ CBD
(Angles opposite to equal sides)
= 30°
But ∠BCD + ∠CBD + ∠BDC = 180° (Angles of a triangle)
=> 30°+ 30°+ ∠BDC = 180°
=> 60°+ ∠BDC = 180°
=> ∠ BDC =180° – 60° = 120°
But ABDC is a cyclic quadrilateral
∠BAC + ∠BDC = 180°
=> ∠BAC + 120°= 180°
=> ∠ BAC = 180° – 120° = 60°
Hence ∠ BAC = 60° Ans.

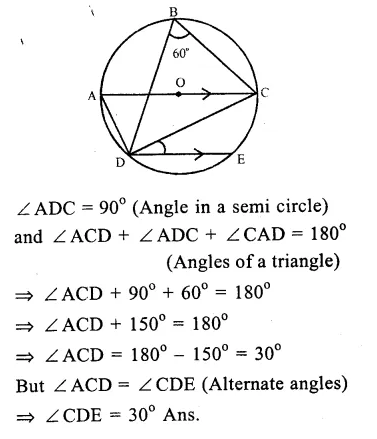
Question 7.
Solution:
(i) Arc ABC subtends ∠ AOC at the centre , and ∠ ADC at the remaining part of the circle.
∠ AOC = 2 ∠ ADC

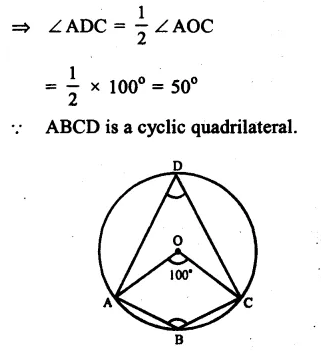
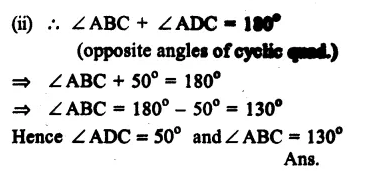
Question 8.
Solution:
In the figure, ABC is an equilateral triangle inscribed is a circle
Each angle is of 60°.
∠ BAC = ∠ BDC
(Angles in the same segment)
∠BDC = 60°
BECD is a cyclic quadrilateral.
∠BDC + ∠BEC = 180°
(opposite angles of cyclic quad.)
=> 60°+ ∠BEC = 180°
=> ∠BEC = 180° – 60°= 120°
Hence ∠BDC = 60° and ∠BEC = 120° Ans.

Question 9.
Solution:
ABCD is a cyclic quadrilateral.
∠BCD + ∠BAD = 180°
(opposite angles of a cyclic quad.)
=> 100°+ ∠BAD = 180°
so ∠BAD = 180° – 100° = 80°
Now in ∆ ABD,
∠BAD + ∠ABD + ∠ADB = 180° (Angles of a triangle)

=> 80° + 50° + ∠ADB = 180°
=> 130°+ ∠ADB = 180°
=> ∠ADB = 180° – 130° = 50°
Hence, ∠ADB = 50° Ans.

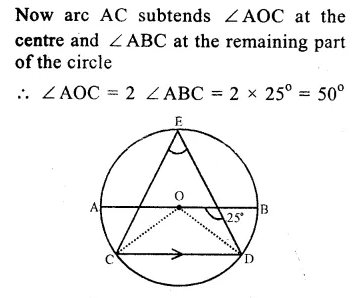
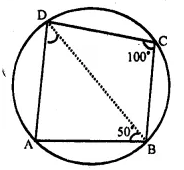
Question 10.
Solution:
Arc BAD subtends ∠ BOD at the centre and ∠BCD at the remaining part of the circle.

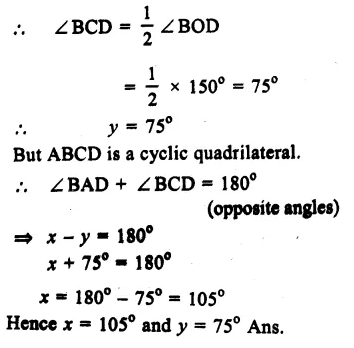
Question 11.
Solution:
In ∆ OAB,
OA = OB (radii of the same circle)
∠OAB = ∠OBA = 50°
and Ext ∠BOD = ∠OAB + ∠OBA
=>x° = 50° + 50° – 100°
ABCD is a cyclic quadrilateral
∠BAD + ∠BCD = 180°
(opposite angles of a cyclic quad.)
=> 50°+ y° = 180°
=> y° = 180° – 50° = 130°
Hence x = 100° and y = 130° Ans.

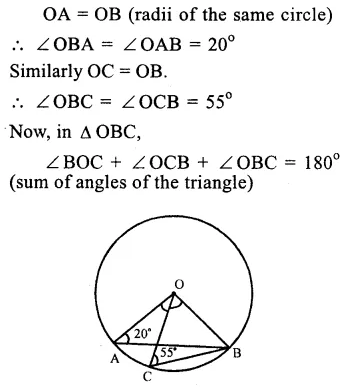
Question 12.
Solution:
Sides AD and AB of cyclic quadrilateral ABCD are produced to E and F respectively.
∠CBF = 130°, ∠CDE = x.
∠CBF + ∠CBA = 180° (Linear pair)
=> 130°+ ∠CBA = 180°
=> ∠CBA = 180° – 130° = 50°
But Ext. ∠ CDE = Interior opp. ∠ CBA (In cyclic quad. ABCD)
=> x = 50° Ans.

Question 13.
Solution:
In a circle with centre O AB is its diameter and DO || CB is drawn. ∠BCD = 120°
To Find : (i) ∠BAD (ii) ABD
(iii) ∠CBD (iv) ∠ADC
(v) Show that ∆ AOD is an equilateral triangle.
(i) ABCD is a cyclic quadrilateral.
∠BCD + ∠BAD = 180°
120° + ∠BAD = 180°

Question 14.
Solution:
AB = 6cm, BP = 2cm, DP = 2.5cm
Let CD = xcm
Two chords AB and CD

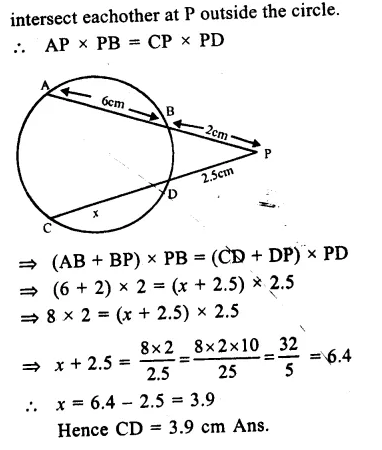
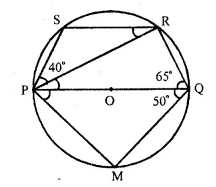
Question 15.
Solution:
O is the centre of the circle
∠ AOD = 140° and ∠CAB = 50°
BD is joined.
(i) ABDC is a cyclic quadrilateral.

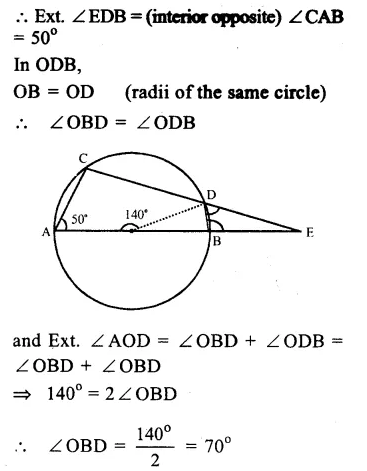
Question 16.
Solution:
Given : ABCD is a cyclic quadrilateral whose sides AB and DC are produced to meet each other at E.
To Prove : ∆ EBC ~ ∆ EDA
Proof : In ∆ EBC and ∆ EDA
∠ E = ∠ E (common)
∠ECB = ∠EAD
{Exterior angle of a cyclic quad, is equal to its interior opposite angle}
and ∠ EBC = ∠EDA
∆ EBC ~ ∆ EDA (AAS axiom)
Hence proved

Question 17.
Solution:
Solution Given : In an isosceles ∆ ABC, AB = AC
A circle is drawn x in such a way that it passes through B and C and intersects AB and AC at D and E respectively.
DE is joined.
To Prove : DE || BC
Proof : In ∆ ABC,
AB = AC (given)
∠ B = ∠ C (angles opposite to equal sides)
But ∠ ADE = ∠ C (Ext. angle of a cyclic quad, is equal E to its interior opposite angle)
∠ADE = ∠B
But, these are corresponding angles
DE || BC.
Hence proved.

Question 18.
Solution:
Given : ∆ ABC is an isosceles triangle in which AB = AC.
D and E are midpoints of AB and AC respectively.
DE is joined.
To Prove : D, B, C, E are concyclic.
Proof: D and E are midpoints of sides AB and AC respectively.
DE || BC
In ∆ ABC, AB = AC
∠B = ∠C
But ∠ ADE = ∠ B (alternate angles)
∠ADE =∠C
But ∠ADE is exterior angle of quad. DBCE which is equal to its interior opposite angle C.
DBCE is a cyclic quadrilateral.
Hence D, B, C, E are con cyclic.
Hence proved.

Question 19.
Solution:
Given : ABCD is a cyclic quadrilateral whose perpendicular bisectors l, m, n, p of the side are drawn

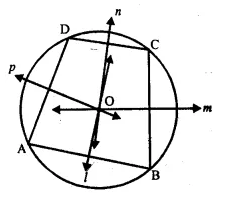
To prove : l, m, n and p are concurrent.
Proof : The sides AB, BC, CD and DA are the chords of the circle passing through the vertices’s of quad. A, B, C and D. and perpendicular bisectors of a chord always passes through the centre of the circle.
l,m, n and p which are the perpendicular bisectors of the sides of cyclic quadrilateral will pass through O, the same point Hence, l, m, n and p are concurrent.
Hence proved.

Question 20.
Solution:
Given : ABCD is a rhombus and four circles are drawn on the sides AB, BC, CD and DA as diameters. Diagonal AC and BD intersect each other at O.

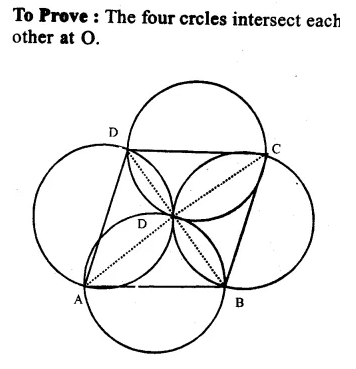
Question 21.
Solution:
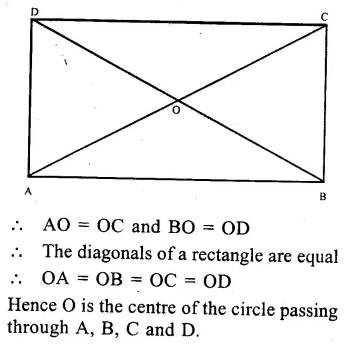
Given: ABCD is a rectangle whose diagonals AC and BD intersect each other at O.
To prove : O is the centre of the circle passing through A, B, C and D

Question 22.
Solution:
Construction.
(i) Let A, B and C are three points
(ii) With A as centre and BC as radius draw an arc
(iii) With centre C, and radius AB, draw another arc which intersects the first arc at D.
D is the required point.
Join BD and CD, AC and BA and CB

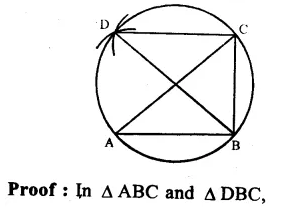
BC = BC (common)
AC = BD (const.)
AB = DC
∴ ∆ ABC ≅ ∆ DBC (SSS axiom)
∴ ∠BAC ≅ ∠BDC (c.p.c.t.)
But these are angles on the same sides of BC
Hence these are angles in the same segment of a circle
A, B, C, D are concyclic Hence D lies on the circle passing througtvA, B and C.
Hence proved.

Question 23.
Solution:
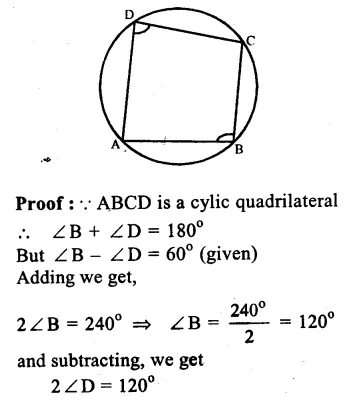
Given : ABCD is a cylic quadrilateral (∠B – ∠D) = 60°
To prove : The small angle of the quad, is 60°

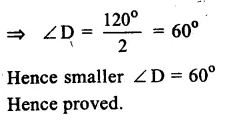
Question 24.

Solution:
Given : ABCD is a quadrilateral in which AD = BC and ∠ ADC = ∠BCD
To prove : A, B, C and D lie on a circle

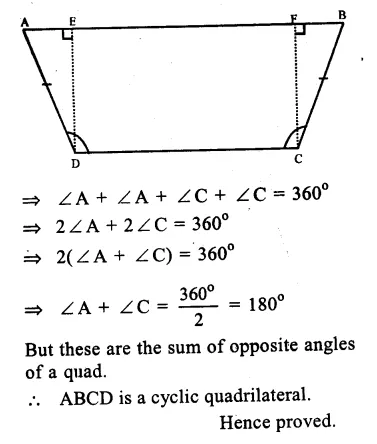
Question 25.
Solution:
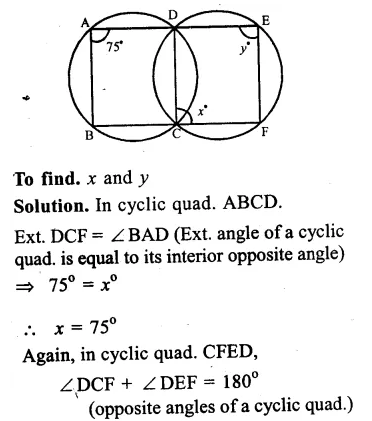
Given : In the figure, two circles intersect each other at D and C
∠BAD = 75°, ∠DCF = x° and ∠DEF = y°

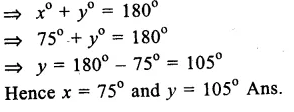
Question 26.
Solution:
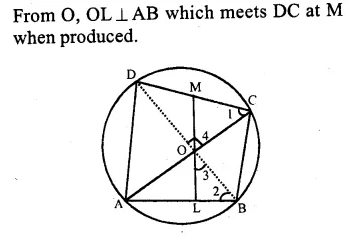
Given : ABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at O at right angle.

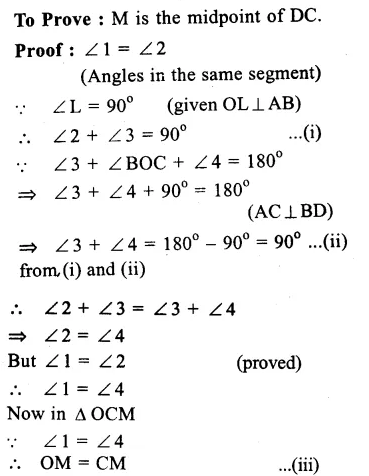
Question 27.
Solution:
In a circle, two chords AB and CD intersect each other at E when produced.
AD and BC are joined.

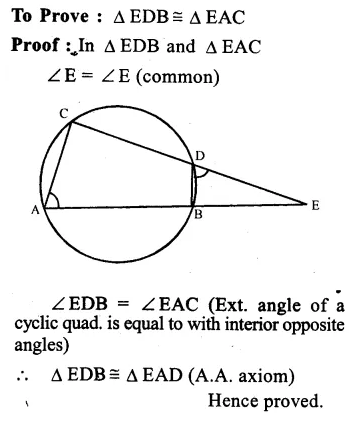
Question 28.
Solution:
Given : Two parallel chords AB and CD of a circle BD and AC are joined and produced to meet at E.

Question 29.
Solution:
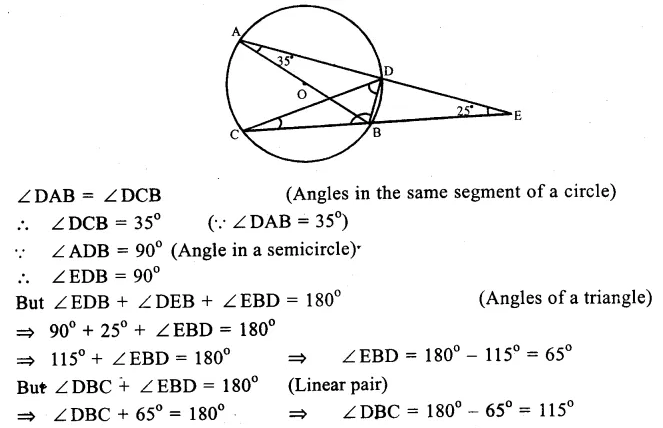
Given : In a circle with centre O, AB is its diameter. ADE and CBE are lines meeting at E such that ∠BAD = 35° and ∠BED = 25°.
To Find : (i) ∠DBC (ii) ∠DCB (iii) ∠BDC
Solution. Join BD and AC,

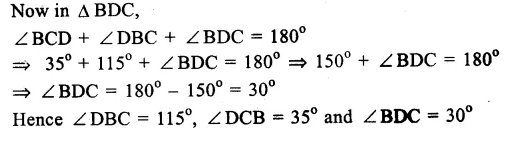
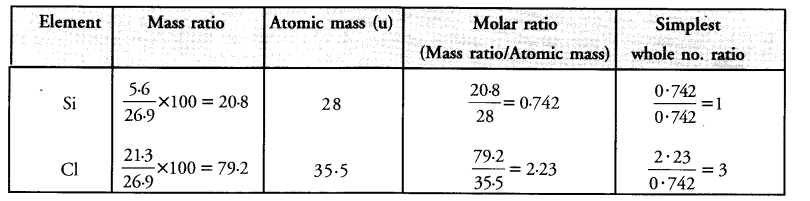
Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C

Question 1.
Solution:
(i) O is the centre of the circle
∠OAB = 40°, ∠OCB = 30°
Join OB.

Question 2.
Solution:
O is the centre of the cirlce and ∠AOB = 70°
∵ Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∵ ∠ACB = \(\frac { 1 }{ 2 } \) ∠AOB = \(\frac { 1 }{ 2 } \) x 70°
=> ∠ACB = 35°
or ∠OCA = 35°
In ∆OAC,
OA = OC (radii of the same circle)
∴ ∠OAC = ∠OCA = 35° Ans.

Question 3.
Solution:
In the figure, O is the centre of the circle. ∠PBC = 25°, ∠APB =110°
∠ APB + ∠ BPC = 180° (Linear pair)
=> 110° + ∠ BPC = 180°

Question 4.
Solution:
O is the centre of the circle
∠ABD = 35° and ∠B AC = 70°
BOD is the diameter of the circle
∠BAD = 90° (Angle in a semi circle)
But ∠ADB + ∠ABD + ∠BAD = 180° (Angles of a triangle)
=> ∠ADB + 35° + 90° = 180°
=> ∠ADB + 125° = 180°
=> ∠ADB = 180° – 125° = 55°
But ∠ACB = ∠ADB (Angles in the same segment of the circle)
∠ACB = 55° Ans.

Question 5.
Solution:
O is the centre of a circle and ∠ACB = 50°
∴ arc AB subtends ∠ AOB at the centre and ∠ ACB at the remaining part of the circle.
∴ ∠ AOB = 2 ∠ ACB
= 2 x 50° = 100
∴ OA = OB (radii of the same circle)
∴ ∠ OAB = ∠ OBA (Angles opposite to equal sides)
Now in ∆ OAB,
∠ OAB + ∠ OBA + ∠ AOB = 180°
=> ∠ OAB + ∠ OAB + ∠ AOB = 180° (∠OAB = ∠OBA)
=> 2 ∠ OAB + 100°= 180°
=> 2 ∠ OAB = 180° – 100° = 80°
=> ∠OAB = \(\frac { { 80 }^{ o } }{ 2 } \) = 40°
Hence, OAB = 40° Ans.

Question 6.
Solution:
(i) In the figure,
∠ABD = 54° and ∠BCD = 43°
∠BAD = ∠BCD (Angles in the same segment of a circle)
∠BAD = 43°

Question 7.
Solution:
Chord DE || diameter AC of the circle with centre O.
∠CBD = 60°
∠CBD = ∠ CAD
(Angles in the same segment of a circle)
∠CAD = 60°
Now in ∆ ADC,

Question 8.
Solution:
In the figure,
chord CD || diameter AB of the circle with centre O.
∠ ABC = 25°
Join CD and DO.
AB || CD
∠ ABC = ∠ BCD (alternate angles)

Question 9.
Solution:
AB and CD are two straight lines passing through O, the centre of the circle and ∠AOC = 80°, ∠CDE = 40°
∠ CED = 90° (Angle in a semi circle)

Question 10.
Solution:
O is the centre of the circle and ∠AOB = 40°, ∠BDC = 100°
Arc AB subtends ∠AOB at the centre and ∠ ACB at the remaining part of the circle
∠ AOB = 2 ∠ ACB

Question 11.
Solution:
Chords AC and BD of a circle with centre O, intersect each other at E at right angles.
∠ OAB = 25°. Join OB.
In ∆ OAB,
OA = OB (radii of the same circle)

Question 12.
Solution:
In the figure, O is the centre of a circle ∠ OAB = 20° and ∠ OCB = 55° .
In ∆ OAB,

Question 13.
Solution:
Given : A ∆ ABC is inscribed in a circle with centre O and ∠ BAC = 30°
To Prove : BC = radius of the circle
Const. Join OB and OC

Question 14.
Solution:
In a circle with centre O and PQ is its diameter. ∠PQR = 65°, ∠SPR = 40° and ∠PQM = 50°
(i) ∠PRQ = 90° (Angle in a semicircle) and ∠PQR + ∠RPQ + ∠PQR = 180° (Angles of a triangle)

Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.