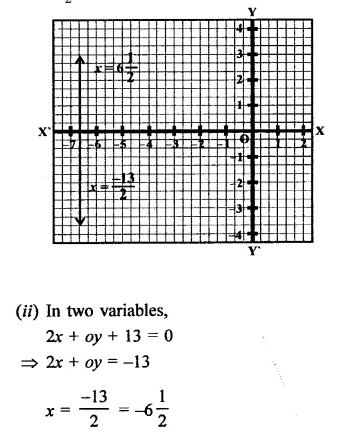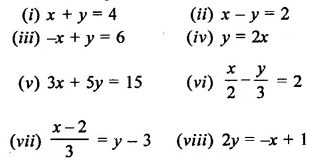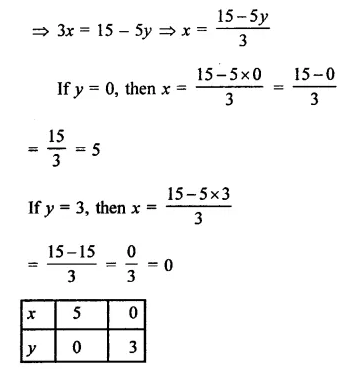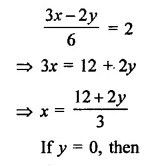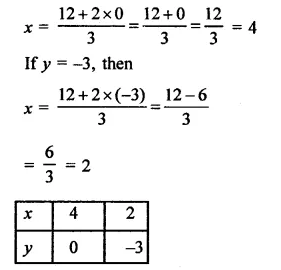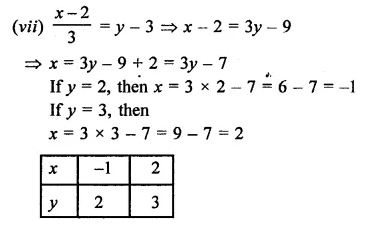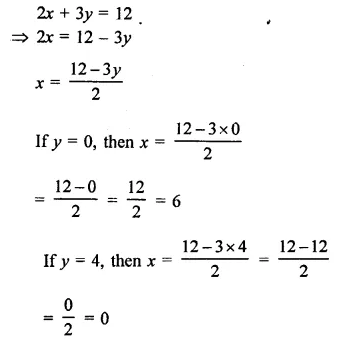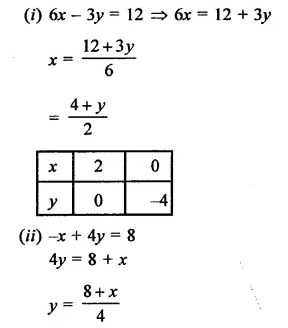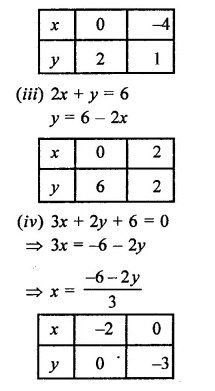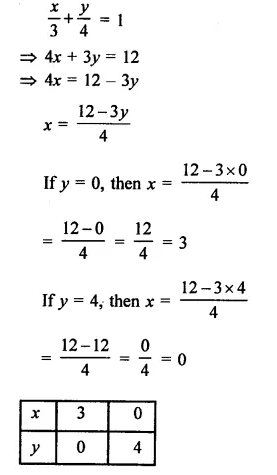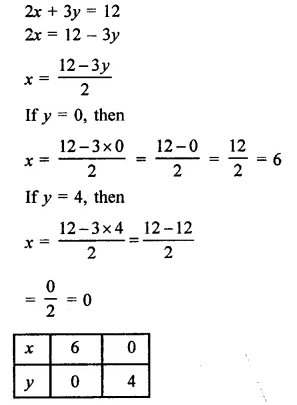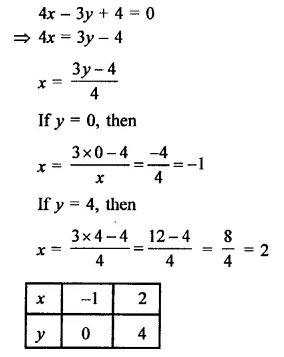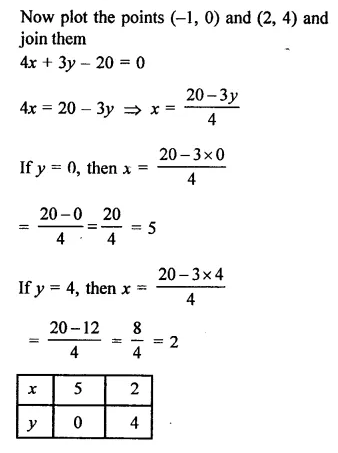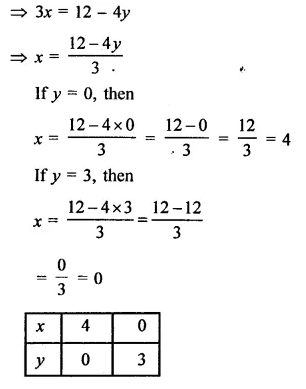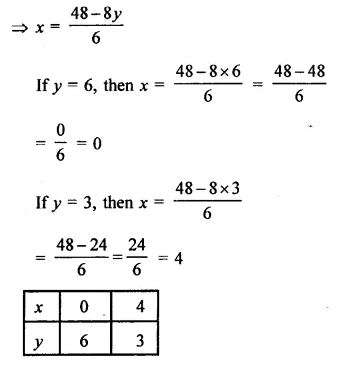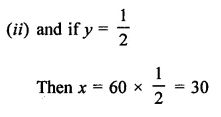CBSE Class 9

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Mark the correct alternative in each of the following:
Question 1.
If (4, 19) is a solution of the equation y = ax + 3, then a =
(a) 3                           
(b) 4
(c) 5            
(d) 6
Solution:
∵  (4, 19) is a solution of equation
y = ax + 3
∴ x = 4, y= 19 will satisfy the equation
∴  19 = a x 4 + 3 = 4a + 3
4a = 19-3 = 16 ⇒ a= \(\frac { 16 }{ 4 }\) = 4
∴  a = 4                                      (b)

Question 2.
If (a, 4) lies on the graph of 3x + y = 10, then the value of a is
(a) 3                           
(b) 1
(c) 2                           
(d) 4
Solution:
∵  (a, 4) is the solution of the equation 3x + y = 10
∴ x = a, y = 4 will satisfy the equation
∴ Substituting the value of x and y in the equation
3 xa + 4= 10 ⇒  3a =10- 4 = 6
⇒  a =  \(\frac { 6 }{ 3 }\) = 2
∴ a = 2                                           (c)

Question 3.
The graph of the linear equation 2x – y= 4 cuts x-axis at
(a) (2, 0)                     
(b) (-2, 0)
(c) (0, -4)                    
(d) (0, 4)
Solution:
∵  graph of the equation,
2x – y = 4 cuts x-axis
∴ y = 0
∴  2x – 0 = 4 ⇒  2x = 4
⇒  x = \(\frac { 4 }{ 2 }\) = 2
∴ The line cuts x-axis at (2, 0)               (a)

Question 4.
How many linear equations are satisfied by x = 2 and y = -3 ?
(a) Only one                
(b)   Two
(c) Three                     
(d)    Infinitely many
Solution:
∵  From a point, infinitely number of lines can pass.
∴  The solution x = 2, y = -3 is the solution of infinitely many linear equations.       (d)

Question 5.
The equation x – 2 = 0 on number line is represented by
(a) aline                      
(b)   a point
(c) infinitely many lines
(d) two lines
Solution:
The equation x – 2 = 0
⇒  x = 2
∴ It is representing by a point on a number line. (b)

Question 6.
x = 2, y = -1 is a solution of the linear equation
(a) x   + 2y  = 0           
(b) x + 2y =  4
(c) 2x + y =  0            
(d) 2x + y =  5
Solution:
x = 2, y = -1
Substituting the values of x and y in the equations one by one, we get (a) x + 2y = 0
⇒ 2 + 2(-1) = 0
⇒ 2 – 2 = 0
⇒ 0 = 0 which is true                             (a)

Question 7.
If (2k – 1, k) is a solution of the equation 10x – 9y = 12, then k =
(a) 1                           
(b) 2
(c) 3                           
(d) 4
Solution:
∵  (2k – 1, k) is a solution of the equation 10x – 9y = 12
Substituting the value of x and y in the equation
10(2k – 1) – 9k = 12
⇒ 20k – 10-9k= 12
⇒  20k – 9k = 12 + 10
⇒  11k = 22
⇒  k =\(\frac { 22 }{ 11 }\)  = 2
∴  k = 2                                                 (b)

Question 8.
The distance between the graph of the equation x = – 3    and x   = 2      is
(a) 1                             
(b) 2
(c) 3                             
(d) 5
Solution:
The distance between the  graphs of the equation
x = -3 and x = 2 will be
2(-3) = 2+ 3 = 5                                     (b) 

Question 9.
The distance   between the graphs of the equations y = -1 and y = 3    is
(a) 2                            
(b) 4
(c) 3                            
(d) 1
Solution:
The distance between the graphs of the equation
y = -1 and y = 3
is 3 – (-1) = 3 + 1 = 4                            (b)

Question 10.
If the graph of the equation 4x + 3y = 12 cuts the co-ordinate axes at A and B, then hypotenuse of right triangle AOB is of length
(a) 4 units
(b) 3 units
(c) 5 units          
(d) none of these
Solution:
Equation is 4x + 3y = 12
If it cuts the x-axis, then y = 0
∴  4x x 3 x 0 = 12
⇒  4x = 12 ⇒  x = \(\frac { 12 }{ 4 }\) = 3
OA = 3 units
∴ The point of intersection of x-axis is (3, 0)
Again if it cuts the y-axis, then x = 0 , Y= 0
∴  4x x 3 x 0 = 12
⇒ 4x = 12 ⇒ x =  \(\frac { 12 }{ 3 }\) = 4
⇒ OB = 4 units
∴ The point of intersection is (0, 4)
∴ In right ΔAOB,
AB² = AO² + OB²
= (3)² + (4)²
= 9 + 16 = 25
= (5)²
∴ AB = 5 units                                        (c)

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Write the equation representing x-axis.
Solution:
The equation of x-axis is, y = 0.

Question 2.
Write the equation representing y-axis.
Solution:
The equation of y-axis is, x = 0.

Question 3.
Write the equation of a line passing through the point (0, 4) and parallel to x-axis.
Solution:
The equation of the line passing through the point (0,4) and parallel to x-axis will be y = 4.

Question 4.
Write the equation of a line passing through the point (3, 5) and parallel to x-axis.
Solution:
The equation of the line passing through the point (3, 5) and parallel to x-axis will be y = 5.

Question 5.
Write the equation of a line parallel toy-axis and passing through the point (-3, -7).
Solution:
The equations of the line passing through the point (-3, -7) and parallel to y-axis will be x = -3.

Question 6.
A line passes through the point (-4, 6) and is parallel to x-axis. Find its equation. A line passes through the point (-4, 6) and is parallel to x-axis. Find its equation.
Solution:
A line parallel to x-axis and passing through the point (-4, 6) will be y = 6.

Question 7.
Solve the equation 3x – 2 = 2x + 3 and represent the solution on the number line.
Solution:
3x – 2 = 2x + 3
⇒  3x – 2x = 3 + 2 (By terms formation)
⇒  x = 5
∴ x = 5
Solution on the number line is

Question 8.
Solve the equation 2y – 1 = y + 1 and represent it graphically on the coordinate plane.

Solution:
2y – 1 = y + 1
⇒ 2y – y = 1 +1
⇒  y = 2
∴ It is a line parallel to x-axis at a distance of 2 units above the x-axis is y = 2.

Question 9.
If the point (a, 2) lies on the graph of the linear equation 2x – 3y + 8 = 0, find the value of a.
Solution:
∵ Points (a, 2) lies on the equation
2x – 3y + 8 = 0
∴ It will satisfy the equation,
Now substituting the value of x = a, y = 2 in the equation
⇒ 2a – 3 x 2+ 8= 0
⇒ 2a + 2= 0
⇒ 2a = -2
⇒ a = \(\frac { -2 }{ 2 }\) = -1
∴ a = -1

Question 10.
Find the value of k for which the point (1, -2) lies on the graph of the linear equation, x – 2y + k = 0.
Solution:
∵ Point (1, -2) lies on the graph of the equation x – 2y + k = 0
∴ x = 1, y = -2 will satisfy the equation
Now substituting the value of x = 1, y = -2 in it
1-2 (-2) + k = 0
⇒  1 + 4 + k = 0
⇒  5+ k = 0 ⇒  k =-5
∴  k = -5

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Give the geometric representations of the following equations.
(a) on the number line
(b) on the cartesian plane.
(i) x – 2
(ii) y + 3 = 0
(iii) y = 3
(iv) 2x + 9 = 0
(v) 3x – 5 = 0
Solution:
(i) x = 2
(i) on the number line

(ii) x = 2 is a line parallel to 7-axis at a distance of 2 units to right of y-axis.

(ii) y = -3 is a line parallel to x-axis at a distance of 3 units below x-axis.

(iii) y = 3
(i) y = 3

(ii) y = 3 is a line parallel to x-axis at a distance of 3 units above x-axis.


x = -4.5 is a line parallel to 7-axis at a distance of 4.5 units to left of y-axis.


(ii) x = 1\(\frac { 2 }{ 3 }\) is a line parallel to y-axis at a  distance of 1\(\frac { 2 }{ 3 }\) unit to right side of y-axis.

Question 2.
Give the geometrical representation of 2x + 13 = 0 as an equation in
(i) One variable
(ii) Two variables
Solution:
(i) In one variable,
2x + 13 = 0
⇒ 2x = – 13
⇒ x = \(\frac { -13 }{ 2 }\)

is a line parallel to y-axis at a distance of -6 \(\frac { 1 }{ 2 }\) units on the left side of y-axis.

Question 3.
Solve the equation 3x + 2 = x -8, and represent on
(i) the number line
(ii) the Cartesian plane.
Solution:
3x + 2 = x – 8
⇒  3x – x = -8 – 2
⇒  2x = -10
⇒  x = \(\frac { -10 }{ 2 }\) = -5
(i) on the number line s = -5

(ii) x = -5 is a line parallel to  y-axis at a distance of 5 knot’s left of y-axis.

Question 4.
Write the equal of the line that is parallel to x-axis and passing through the points.
(i) (0, 3)                     
(ii)  (0, -4)
(iii) (2, -5)                     
(iv)    (3, 4)
Solution:
∵  A line parallel to x-axis will be of the type y = a
∴ (i) y = 3
(ii) y = -4
(iii) y = -5 and y = 4 are equations of the lines parallel to x-axis

Question 5.
Write the equation of the line that is parallel to y-axis and passing through the points.
(i) (4, 0)                      
(ii) (-2, 0)
(iii) (3, 5)                    
(iv) (-4, -3)
Solution:
∵  A line parallel to y-axis will be of the type x = a
∴  (i) x = 4, (ii)  x = -2, x = 3 and x = -4 are the equations of the lines parallel to y-axis.

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Draw the graph of each of the following linear equations in two variables.

Solution:
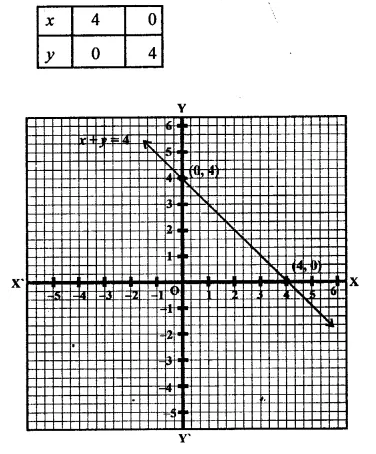
(i)x + y = 4
x = 4 – y
If y = 0, then x = 4
If y = 4, then x = 0
Now plot the points (4, 0) and (0, 4) on the graph and join them ro get the graph of the given equation

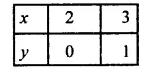
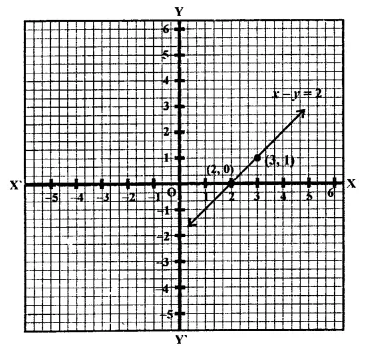
(ii)x – y = 2
x = 2 +y
If y = 0, then x = 2 and if y = 1,
Then x = 2 + 1 = 3

Now plot the points (2, 0) and (3, 1) on the graph and join them to get the graph of the equation.

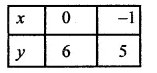
(iii) -x+y = 6 ⇒  y = 6+x

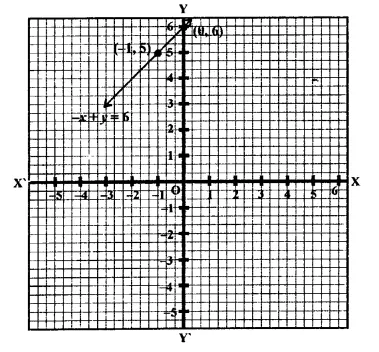
If x = 0, then y = 6 + 0 = 6
If x = -1, then y = 6 – 1 = 5

Now plot the points (0, 6) and (-1, 5) on the graph and join them to get a graph of the line.
(iv) y = 2x
If x = 0, then y =  2 x 0 = 0
If x = 1, then y = 2 x 1 = 2


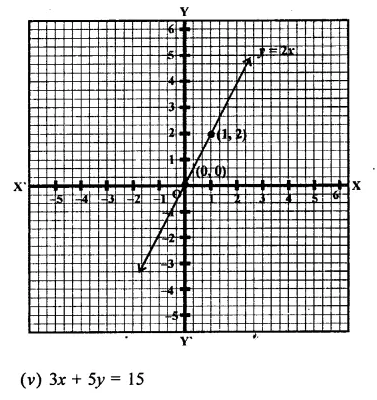
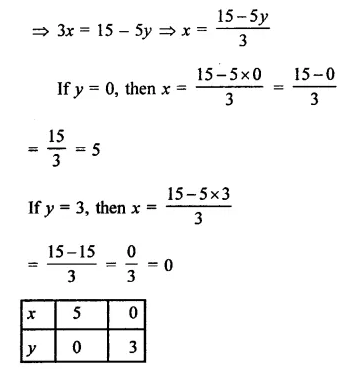
Now plot the points (0, 0) and (1, 2) on the graph and join them to get the graph of the line.


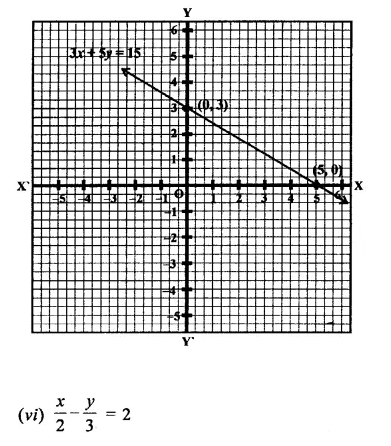
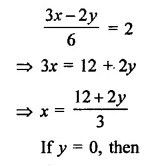
Now plot the points (5, 0) and (0, 3) on the graph and join them to get the graph of the line.

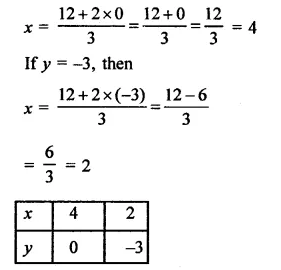
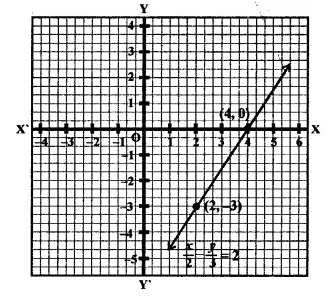
Now plot the points (4, 0) and (2, -3) on the graph and join them to get the graph of the line.


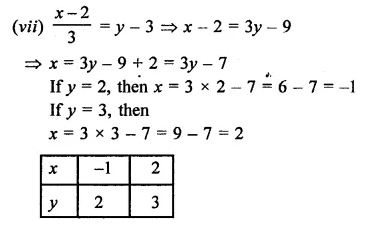
Now plot the points (-1, 2) and (2, 3) on the graph and join then to get the graph of the line.


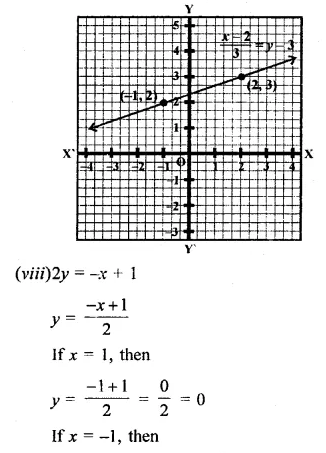
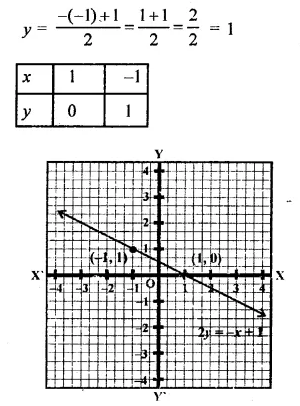
Now plot the points (1, 0) and (-1, 1) on the graph and join then to get the graph of the line.

Question 2.
Give the equations of two lines passing through (3, 12). How many more such lines are there, and why ?
Solution:
∵  Points (3, 12) lies on the lines passing through the points
∴ Solutions is x = 3,y- 12
∴  Possible equation can be
x + y = 15
-x+y = 9
4x-y = 0
3x – y + 3 = 0

Question 3.
A three-wheeler scooter charges ₹15 for first kilometer and ₹8 each for every subsequent kilometer. For a distance of x km, an amount of ₹y is paid. Write the linear equation representing the above information.
Solution:
Charges for the first kilometer = ₹15
Charges for next 1 km = ₹8
Distance = x km
and total amount = ₹y
∴ Linear equation will be,
15 + (x- 1) x 8 =y
⇒  15 + 8x – 8 = y
⇒   7 + 8x = y
∴  y = 8x + 7

Question 4.
Plot the points (3, 5) and (-1, 3) on a graph paper and verify that the straight line passing through these points also passes through the point (1, 4).
Solution:

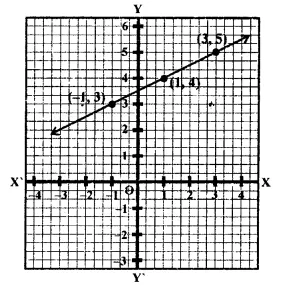
Points (3, 5) and (-1, 3) have been plotted on the graph and joined to get a line. We see that die point (1,4) also lies out.

Question 5.
From the choices given below, choose the equation whose graph is given in figure.
(i) y = x                   
(ii) x + y = 0
(iii) y = 2x                   
(iv) 2 + 3y = 7x
Solution:

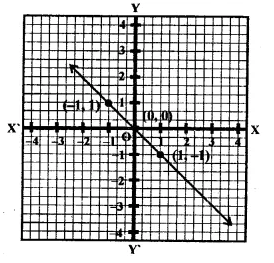
From the graph, we see that Points (-1, 1) and (1, -1) be on the graph of the line these will satisfy the equation of the line
∴  -x = y ⇒ x+ y = 0
i.e, required equation
∵ x + y = 0 is the graph of the equation.

Question 6.
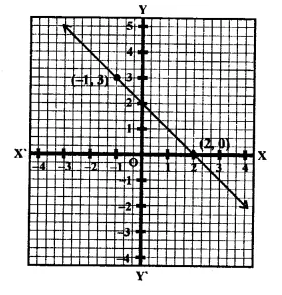
From the choices given below, choose the equation whose graph is given in figure.
(i) y = x + 2              
(ii) y = x – 2
(ii) y = -x + 2           
(iv) x + 2y = 6
Solution:
From the graph
Points (-1,3) and (2, 0) lie on the graph of the line
Now there points, by observation, satisfy the equation y= -x+2
∴ Required equation is y = -x + 2 whose graph is given.

Question 7.
If the point (2, -2) lies on the graph of the linear equation 5x + ky =4, find the value of k.
Solution:
∵  Point (2, -2) lies on the graph of the linear equation 5x + ky = 4
∴  It will satisfy it
∴ Now substituting the values of x and y 5 x 2 + k (-2) = 4
⇒ 10 – 2k = 4 ⇒  -2k = 4 – 10 = -6 -6
⇒ k= \(\frac { -6 }{ -2 }\) =3
Hence k = 3

Question 8.
Draw the graph of the equation 2x + 3p = 12. From the graph find the co-ordinates of the point.
(i) whose y -coordinates is 3
(ii) whose x-coordinates is -3
Solution:


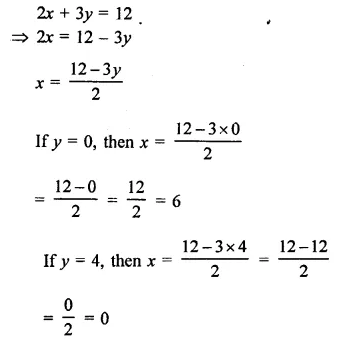
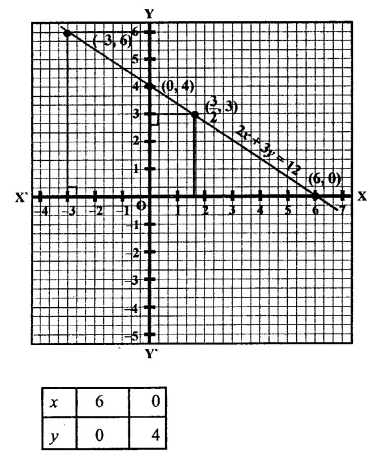
Plot the points (6, 0) and (0, 4) on the graph and join them to get the graph if the line.
(i) If y = 3, then draw perpendicular from y = 3 to the line, which get meets it at P then x-coordinate of p will be
∴ coordinates of P are ( \(\frac { 3 }{ 2 }\) ,3)
(ii) If x = -3, draw perpendicular from x = -3 to the line, which meets it Q.
The y coordinates of Q will be y = 6
∴ co-ordinates of Q are (-3, 6)

Question 9.
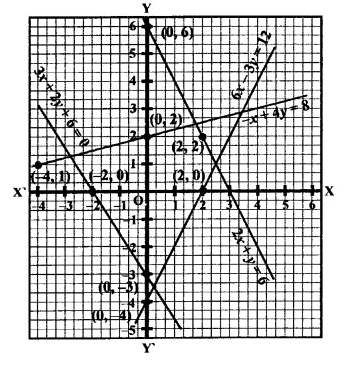
Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinates axes:
(i) 6x – 3y = 12        
(ii) -x + 4y = 8
(iii) 2x + y = 6          
(iv) 3x + 2y + 6 = 0
Solution:


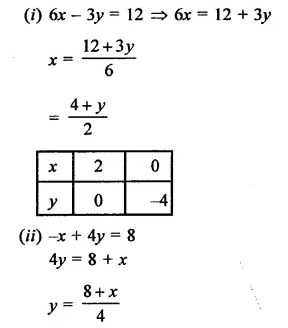
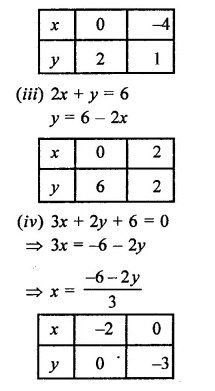
Now plot the points of each equation and join then we get four lines as shown on the graphs.
Equation (i) cuts the axes at (2, 0) and (0, -4)
Equation (ii) cuts the axes at (-8, 0) and (0, 2)
Equation (iii) cuts the axes at (3, 0), (0, 6) and
Equation (iv), cuts the axes at (-2, 0) and (0,-3)

Question 10.
A lending library has a fixed charges for the first three days and an additional charge for each day thereafter. Aarushi paid ₹27 for a book kept for seven days. If fixed charges are ₹x and per day charges are ₹y. Write the linear equation representing the above information.
Solution:
Let fixed charges for first 3 days = ₹x
and additional charges for each day = ₹y
Total period = 7 days
and amount charges = ₹27
∴ x + (7 – 3) x y  = 27
⇒  x + 4y = 27
Hence x + 4y = 27

Question 11.
A number is 27 more than the number obtained by reversing its digits. If its unit’s and ten’s digit are x and y respectively, write the linear equation representing the above statement.
Solution:
Let unit’s digit = x
and tens digit = y
∴  Number = x + 10y
By reversing the digits, units digit = y
and ten’s digit = x
∴  number = y + 10x
Now difference of these two numbers = 27 (x + 10y) – (y +10x) = 27
x + 10y – y – 10x = 27
⇒  -9x + 9y – 27 = 0
⇒ x-_y + 3 = 0                   (Dividing by -9)
Hence equation is x – y + 3 = 0

Question 12.
The sum of a two digit number and the number obtained by reversing the order of its digits is 121. If units and ten’s digit of the number are x and y respectively, then write the linear equation representing the above statement.
Solution:
Let unit digit = x
and tens digit = y
∴ Number = x + 10y
By reversing the digits,
units digit = y
and tens digit = x
∴ Number =y+ 10x
Now sum of these two numbers = 121
∴ x + 10y + y + 10x = 121
⇒  1 lx + 11y = 121
⇒  x + y = 11                        (Dividing by 11)
∴  x + y = 11

Question 13.
Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also find the area of the shaded region.
Solution:
2x + y = 6
⇒  y = 6 – 2x
If x = 0, then y = 6- 2 x 0 = 6 – 0 = 6
If x = 2, then y = 6- 2 x 2 = 6- 4 = 2

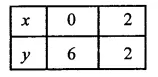
Now plot the points (0, 6) and (2, 2) on the graph and join them to get a line which intersects x-axis at (3, 0) and y-axis at (0,6)
Now co-ordinates if vertices of the shaded portion are (6, 0) (0, 0) and (3, 0) Now area of the shaded region.

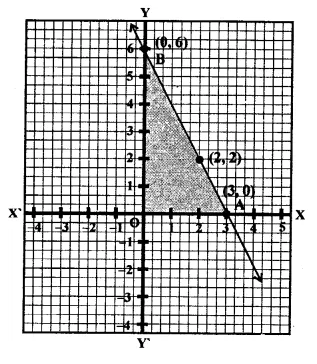
Question 14.
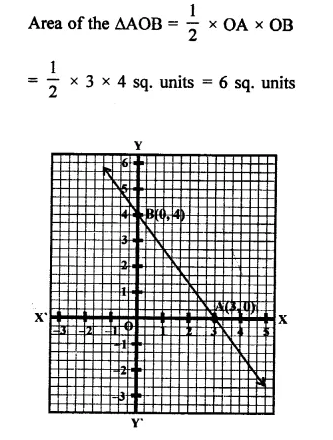
Draw the graph of the equation  \(\frac { x }{ 3 }\) +  \(\frac { y }{ 4 }\)  = 1 Also find the area of the triangle formed by the line and the co-ordinate axes.
Solution:

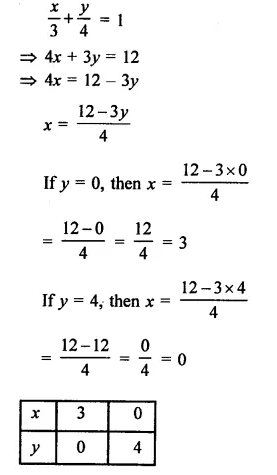
Now plot the points (3, 0) and (0, 4) and join them to get a line which interest x-axis at A (3, 0) and y-axis at B (0, 4)

Question 15.
Draw the graph of y = | x |
Solution:
y = | x |

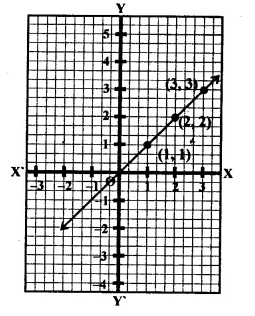
⇒   y = x       [∵ | x |=x]
∴  Now taking z points.


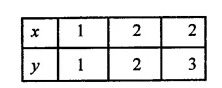
Now plot the points (1, 1) (2, 2) and (3, 3) and join them to get a graph of a line.

Question 16.
Draw the graph of y = | x | + 2
Solution:
y – | x | + 2
⇒  y = x + 2         [| x | = x]
If x = 0, then y = 0 + 2 = 2
If x = 1, then y = 1+2 = 3
If x = 2, then y = 2 + 2 = 4

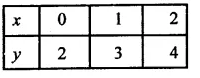
Now plot the points (0, 2), (1, 3) and (2, 4) on the graph and join them to get a line.

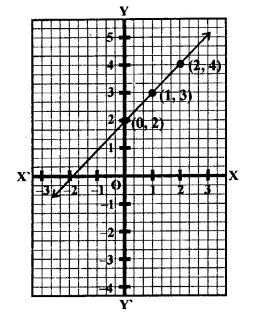
Question 17.
Draw the graphs of the following linear equation on the same graph paper.
2x + 3y = 12, x -y = 1
Find the co-ordinates of the vertices of the triangle formed by the two straight lines and the y-axis. Also find the area of the triangle.
Solution:

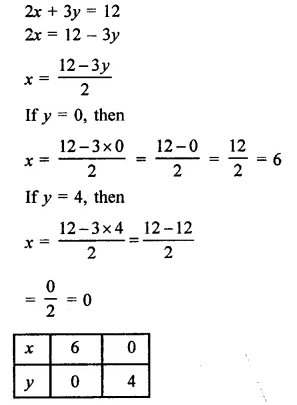
Now plot the points (6, 0) (0, 4) on the graph to get a line.

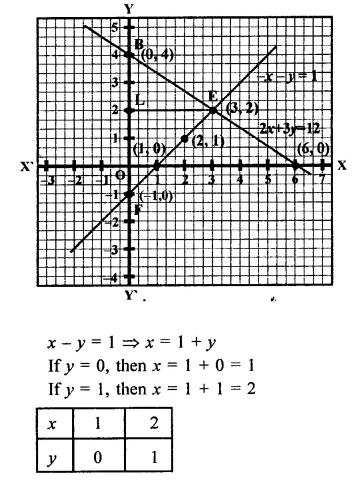
Now plot the points (1, 0) and (2, 1) on the graph to get another line.
Area of the triangle FEB so formed,
= \(\frac { 1 }{ 2 }\) FB x FL = \(\frac { 1 }{ 2 }\) x 5 x 3
= \(\frac { 15 }{ 2 }\)
= 7.5 sq. units
co-ordinates of E, F, B are E (3, 2), (0, -1) and (0, 4)

Question 18.
 Draw the graphs of the linear equations 4x – 3y + 4 = 0 and 4x + 3y – 20 = 0. Find the area bounded by these lines and x-axis.
Solution:



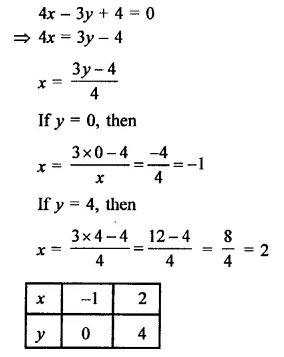
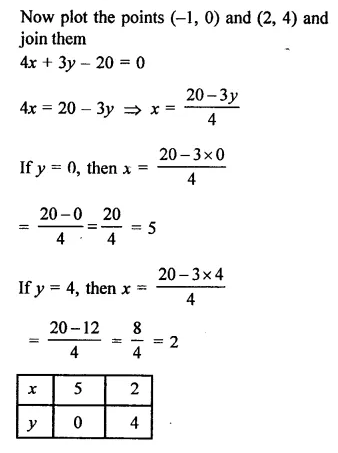
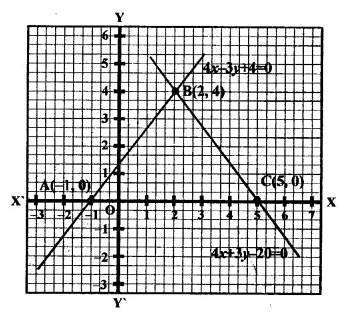
Now plot the points (5, 0) and (2, 4)and join them to get a line we see that the ΔABC is formed by bounding there line with x-axis.

Question 19.
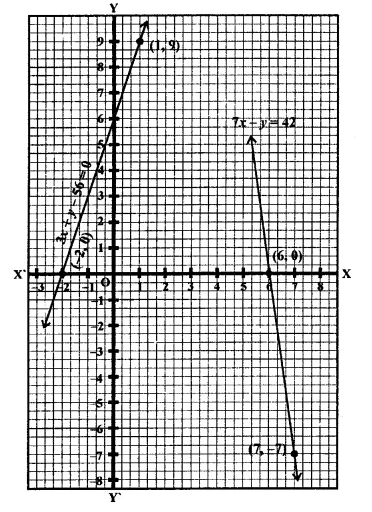
The path of a train A is given by the equation 3x + 4y – 12 = 0 and the path of another train B is given by the equation 6jc + 8y – 48 = 0. Represent this situation graphically.
Solution:
Path of the train A = 3x + 4y – 12 = 0
Path of the train B = 6x + 8y – 48 = 0
Now, 3x + 4y – 12 = 0


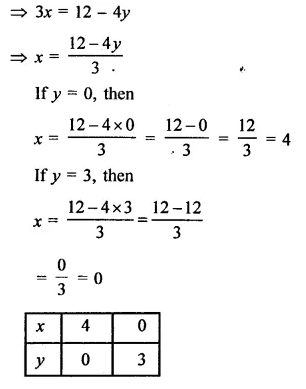
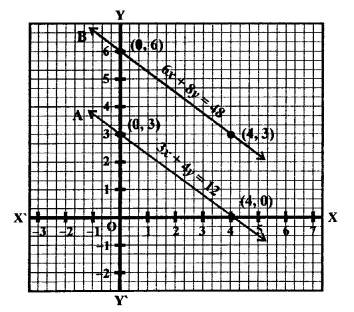
Now plot the points (4, 0) and (0, 3) on the graph and join them to get a line, and 6x + 8y – 48 = 0
⇒  6x = 48 – 8y

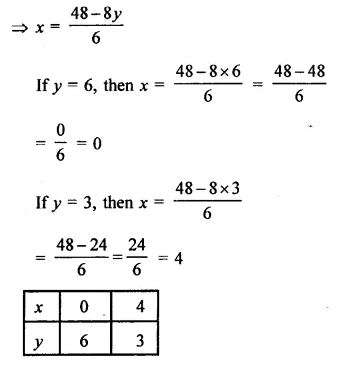
Now plot the points (0, 6) and (4, 3) on the graph and join them to get another line.

Question 20.
Ravish tells his daughter Aarushi, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. If present ages of Aarushi and Ravish are x and y years respectively, represent this situation algebraically as well as graphically.
Solution:
Present age of Aarushi = x years
and age of Ravish = y years
7 years ago,
age of Aarushi = x – 7
years and age of Ravish =y-7 years
∴ y- 7 = 7 (X – 7)
⇒  y – 7 = 7x – 49
⇒  7x – y = -7 + 49  = 42
7x – y = 42
⇒  y = 7x – 42
If x = 6, then
y = 7 x 6 – 42 = 42 – 42 = 0,
If x = 7, then
y = 7 x 7 – 42 – 49 – 42 = -7

Plot the points (6, 0) (7, -7) on the graph and join them.
After 3 years,
age of Aarushi = x + 3
and age of Ravish = y + 3
⇒  y + 3 = 3(x + 3)
⇒ y + 3 = 3x + 9
⇒ y = 3x+ 9-3
⇒ y = 3x + 6
If x = -2, then y = 3 x (-2) + 6 =6-6=0
If x = 1, then y = 3 x (1) + 6 =3+6=9

Plot the points (1, 9), (-2, 0) on the graph Arundeep’s Mathematics (R.D.) 9th and join them to get another line.

Question 21.
Aarushi was driving a car with uniform speed of 60 km/h. Draw distance-time graph. From the graph, find the distance travelled by Aarushi in.
(i) 2\(\frac { 1 }{ 2 }\) Hours             
(ii) \(\frac { 1 }{ 2 }\) Hour
Solution:
Speed of car = 60 km / h.

Now plot the points (60, 1), (120, 2) are the graph and join then to get the graph of line.
From the graph, we see that

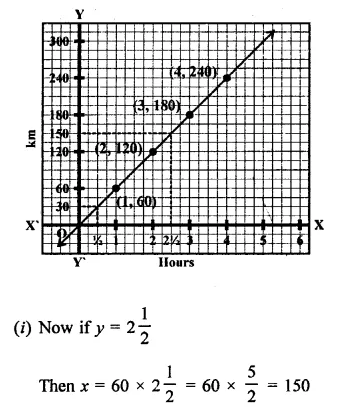
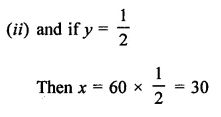
Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.