NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms
These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms
Question 1.
Write true (T) or false (F)
(a) Wittaker proposed five kingdom classification.
(b) Monera is divided into Archaebacteria and Eubacteria.
(c) Starting from Class, Species comes before Genus.
(d) Anabaena belongs to kingdom Monera.
(e) Blue-green algae belong to kingdom Protista.
(f) All prokaryotes are classified under Monera.
Answer:
(a) —T
(b) —T,
(c) — F
(d) —T,
(e) —F,
(f) —T.
More Resources
- NCERT Exemplar Solutions for Class 9 Science
- NCERT Solutions for Class 9 Science
- Value Based Questions in Science for Class 9
- HOTS Questions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
Question 2.
Fill in the blanks :
(a) Fungi show ……………. mode of nutrition.
(b) Cell wall of fungi is made up of ……………… .
(c) Association between blue-green algae and fungi is called as …………….. .
(d) Chemical nature of chidn is ……………… .
(e) ………………. has smallest number of organisms with maximum number of similar characters.
(f) ……………… are called amphibians of plant kingdom.
Answer:
(a) saprophytic
(b) chitin
(c) lichen
(d) carbohydrate
(e) Species
(f) Bryophytes.
Question 3.
You are provided with seeds of Gram, Wheat, Rice Pumpkin, Maize and Pea. Classify them whether they are monocot or dicot ?
Answer:
Gram-Dicot.
Wheat-Monocot.
Rice-Monocot.
Pumpkin-Dicot.
Maize-Monocot.
Pea-Dicot.
Question 4.
Match the items of Column A with items of Column B.

Answer:
(a) —(ii),
(b) —(i),
(c) — (iv),
(d) —(iii),
(e) — (vi),
(f) —(v),
(g) — (vii).
Question 5.
Match the articles of Column A with those of column B

Answer:
a —(iii),
b —(ii),
c—(vi),
d —(i),
e —(v),
f—(iv).
Question 6.
Classify the following organisms based on absence or presence of true coelom as acoelomate, pseudocoelomate and coelomate : Spongilla, Sea Anemone, Planaria, Liver Fluke, Wuchereria, Ascaris, Nereis, Earthworm, Scorpion, Birds, Fishes and Horse.
Answer:
- Spongilla-Acoelomaxe
- Sea Anemone-Acoelomate
- Planaria-Acoelomate
- Liver Fluke-Acoelomate
- Wuchereria— Pseudocoelomate
- Aszvzris-Pseudocoelomate
- Nereis-Coelomate
- Scorpion—Coelomate
- Earthworm-Coelomate
- Birds-Coelomate
- Fishes-Coelomate
- Horse-Coelomate.
Question 7.
Endoskeleton of fishes is made up of cartilage and bone. Classify the following fishes as cartilaginous or bony : Xorpedo, Sting Ray, Dog fish, Rohu, Angler Fish, Exocoetus.
Answer:
- Xorpedo—Cartilaginous
- Sting Ray-Cartilaginous
- Dog Fish-Cartilaginous
- Rohu-Bony
- Angler fish-Bony
- Exocoetus—Bony.
Question 8.
Classify the following based on number of chambers in their heart : Rohu, Scolidon, Salamander, Flying Lizard, King Cobra, Crocodile, Ostrich, Pigeon, Bat, Whale.
Answer:
- Rohu. 2-Chambered.
- Scoliodon. 2-chambered
- Frog. 3-chambered
- Salamander. 3-chambered
- Flying Lizard. Incompletely 4-chambered.
- King Cobra. Incompletely 4-chambered.
- Crocodile. 4-chambered
- Ostrich. 4-chambered
- Pigeon. 4-chambered
- Bat. 4-chambered
- Whale. 4-chambered.
Question 9.
Classify Rohu, Scoliodon, Flying Lizard, King Cobra, Frog, Salamander, Ostrich, Pigeon, Bat, Crocodile and Whale into cold blooded and warm blooded animals.
Answer:
- Rohu. Cold blooded
- Scoliodon. Cold blooded
- Flying Lizard. Cold blooded
- King Cobra. Cold Blooded
- Frog. Cold blooded
- Salamander. Cold blooded
- Ostrich. Warm blooded
- Pigeon. Warm blooded
- Bat. Warm blooded,
- Crocodile. Cold blooded
- Whale. Warm blooded.
Question 10.
Name two egg laying mammals.
Answer:
- Duck Billed Platypus
- Echidna
Question 11.
Fill in the blanks.
(a) Five Kingdom classification of living organisms is given by …………….. .
(b) Basic smallest unit of classification is …………. .
(c) Prokaryotes are grouped in kingdom …………. .
(d) Paramoecium is a protistan because of its ……………. .
(e) Fungi do not contain ……………. .
(f ) A fungus ………….. can be seen without microscope.
(g) Common fungus used in preparing the bread is …………… .
(h) Algae and fungi form symbiotic association called ……………. .
Answer:
(a) Whittaker
(b) species
(c) Monera
(d) unicellular eukaryotic nature
(e) chlorophyll
(f) like mushroom
(g) Yeast
(h) lichen.
Question 12.
Give True (T) and Flase (F) :
(a) Gymnosperms differ from angiosperms in having covered seeds.
(b) Non-flowering plants are called cryptogamae.
(c) Bryophytes have conducting tissue.
(d) Funaria is a moss.
(e) Compound leaves are found in many ferns.
(f) Seeds, contain embryo.
Answer:
(a) —F,
(b) —F,
(c) —F,
(d) —T,
(e) —T,
(f) —T.
Question 13.
Give examples for the following :
(a) Bilateral, dorsiventral symmetry is found in ……………. .
(b) Worm causing disease elephantiasis is ……………… .
(c) Open circulatory system is found in ………………. where coelomic cavity is filled with blood.
(d) …………….. are known to have pseudocoelom.
Answer:
(a) Liver Fluke/Lizard
(b) Wuchereria (Filarial Worm)
(c) Arthropods
(d) Nematodes (roundworms).
Question 14.
Label a, b, c and d in the given figure. Give the function of b.
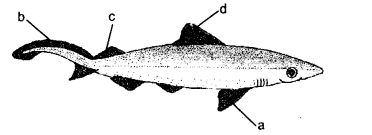
Answer:
a —pectoral fin.
b —caudal fin.
c—posterior dorsal fin,
d —anterior dorsal fin.
Function of b. Swimming and steering.
Question 15.
Fill the boxes with appropriate characteristics/plant group(s)
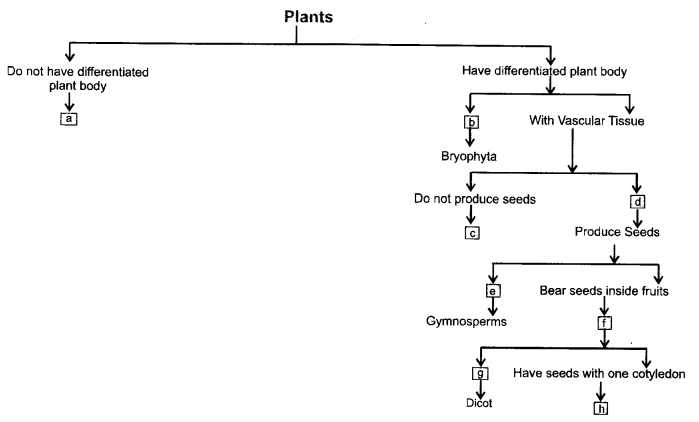
Answer:
a —Thallophyta.
b —Without specialized vascular tissue (non-vascular)
c —Pteridophyta.
d —Phanerogemae.
e —Bear naked seeds.
f—Angiosperms.
g—Have seeds with two cotyledons,
h —Monocots.
Question 16.
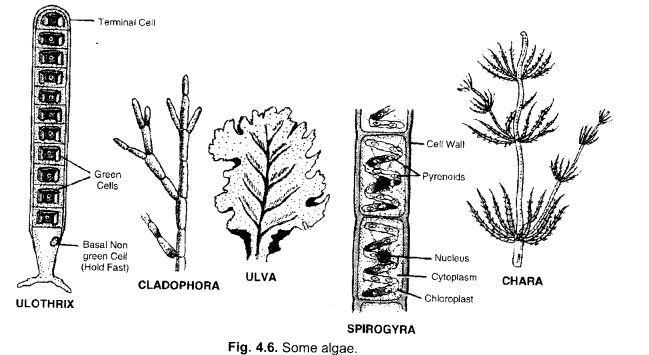
Write name of a few thallophytes. Draw a labelled diagram of Spirogyra.
Answer:
Ulothrix, Cladophora, JJlva, Spirogyra, Chara,
Question 17.
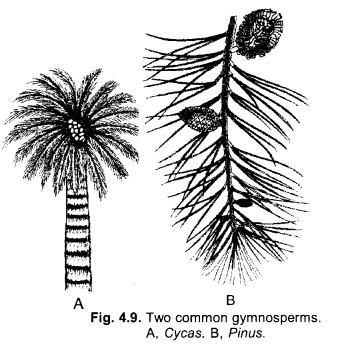
Thallophyta, bryophyta and pteridophyta one called “cryptogams.” Gymnosperms and angiosperns are called “phanerogams”. Discuss why ? Draw one example of gymnosperm. (CCE 2011)
Answer:
(a) Thallophyta, bryophyta and pteridophyta are called cryptogams because they are seedless and possesss inconspicuous or hidden reproductive organs.
(b) Gymnosperms and angiosperms are called phanerogams as they have conspicuous reproductive organs with seeds containing an embryo and reserve food.
(c)
Question 18.
Define the terms and give one example of each
(a) Bilateral symmetry
(b) Coelom
(c) Triploblastic. (CCE 2011, 2012)
Answer:
(a) Bilateral Symmetry: It is a type of symmetry in which appendages and organs of the body are paired with one of each pair being present in right and left halves of the body, e.g., Lizard, Human.
(b) Coelom: It is mesoderm lined, fluid filled internal body cavity that lies between alimentary canal and skin. It provides a shock proof environment to the contained body organs, e.g, chordates, annelids.
(c) Triploblastic: They are animals having three germinal layers — outer ectoderm, middle mesoderm and inner endoderm, e.g, nematodes, arthropods, star fish.
Question 19.
You are given Leech, Nereis, Scolopendra, Prawn and Scorpio/i. All have segmented body organisation. Will you classify them in one group ? If not give the important characters based on which you will separate these, organisms into different groups.
(CCE 2012)
Answer:
No,
- Leech and Nereis have metameric segmentation (external segmentation corresponding to internal segmentation), closed circulatory system and unjointed appendages. They belong to annelida.
- Scolopendra, Prawn and Scorpion have open circulatory system and jointed appendages. They belong to arthropoda.
Question 20.
Which organism is more complex and evolved among bacteria, Mushroom and Mango tree ? Give reasons. (CCE 2012)
Answer:
Mango tree is more complex and evolved among bacteria, Mushroom and Mango because of the
- Differentiated sporophyte
- Vascular tissues
- Embryo stage
- Seeds present inside fruit. Bacteria are procaryotic. Mushroom is eucaryotic (fungus) but without any differentiation of stem leaves and roots, absence of vascular tissues and embryo stage.
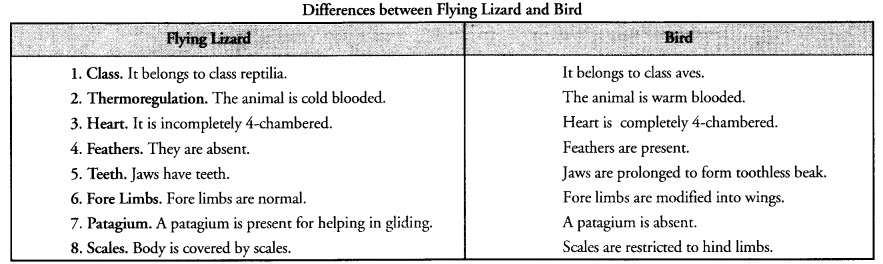
Question 21.
Differentiate between flying Lizard and Bird. Draw the diagram.
Answer:
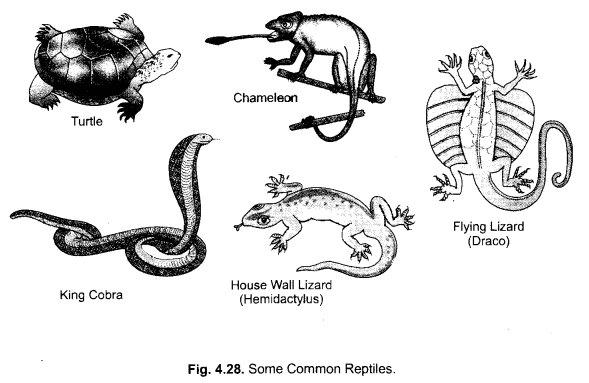

Question 22.
List out some common features in Cat, Rat and Bat. (CCE2012, 2013)
Answer:
Cat, Rat and Bat belong to same class of mammalia. The common features are
- Hair
- Mammary glands
- Integumentary glands
- Seven cervical vertebrae
- Diaphragm
- 4-Chambered heart
- External pinnae
- Vivipary.
Question 23.
Why do we keep both snake and turtle in the same class ? (CCE 2012)
Answer:
Both Snake and Turtle have been placed in class reptilia because of the common characteristics :
- Skin without glands
- Three chambered (incompletely four chambered) heart
- Respiration through lungs
- Cold blooded
- Hard shelled eggs
- Embryo protected by extra embryonal membranes.
Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.