NCERT Solutions for Class 9 Science Chapter 13 Why Do we Fall Ill
These Solutions are part of NCERT Solutions for Class 9 Science. Here we have given NCERT Solutions for Class 9 Science Chapter 13 Why Do we Fall Ill. LearnInsta.com provides you the Free PDF download of NCERT Solutions for Class 9 Science (Biology) Chapter 13 – Why Do We Fall ill solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 13 – Why Do We Fall ill Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks.
More Resources
- NCERT Solutions for Class 9 Science
- HOTS Questions for Class 9 Science
- Value Based Questions in Science for Class 9
- NCERT Exemplar Solutions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
NCERT TEXT BOOK QUESTIONS
IN TEXT QUESTIONS
Question 1.
State any two conditions essential for good health.
- Complete physical fitness free from any disease.
- Perfect mental (and social) well being.
Answer:
State any two conditions essential for being free of disease.
- Non-overcrowded living conditions, safe drinking water and clean environment.
- Balanced diet, personal hygiene, exercise and relaxation.
Question 2.
Are the answers to the above questions same or different ? Why ?
Answer:
Different: Health is a state of perfect physical, mental, and social well being of a person while disease is a state of disease or discomfort of the body or its part.
Question 3.
List any three reasons why you would think that you are sick and ought to see a doctor. If only one of these symptoms were present, would you still go to the doctor ? Why or why not ?
Answer:
- Cough, cold and fever. The sickness must be due to infection which requires proper diagnosis and treatment which only doctor can do.
- If only one symptom is present (say cough only or cold only) even then I will prefer to get treatment from the doctor because an untreated infection can spread and cause further damage to the body.
Question 4.
In which of the following case do you think the long term effects on your health are likely to be most unpleasant ?
Answer:
(a) If you get jaundice
(b) If you get lice
(c) If you get acne.
Jaundice. It is a severe disease which also takes several days to heal. During this period bile pigments collect at several places in the body and permanently damage some of them.
Question 5.
Why are we normally advised to take bland and nourishing food when we are sick ? (CCE 2011, 2012)
Answer:
It helps in strengthening of the immune system and provides nourishment to body which is being depleted by infectious agent.
Question 6.
What are the different means by which infectious diseases are spread ?
Answer:
By air directly or as droplets, e.g., cold.
By contaminated food and water, e.g., cholera.
By fomites or articles contaminated by the patient, e.g., chicken-pox.
Question 7.
Contagious diseases simply spread by contact.
Answer:
By sexual and blood contact in case of AIDS, syphilis and some other diseases.
By vectors and carriers, e.g., malaria by female Anopheles.
Question 8.
What precautions would you take in your school to reduce incidence of infectious diseases ?
Answer:
- Airy and well-spaced classrooms.
- Advising students falling sick not to come to school. If any such student does come, the same should be provided a separate bench.
- Ensuring safe drinking water.
- Cleanliness.
- Protection against flies and mosquitoes.
- Vaccination against diseases.
- Regular medical examination of students.
Question 9.
What is immunisation ?
Answer:
Development of immunity or resistance against a pathogen through vaccination is called immunisation.
Question 10.
What are the immunisation programmes available at our nearest health centre in your locality ?
Which of these diseases are two major health problems in your area ?
Answer:


NCERT CHAPTER END EXERCISES
Question 1.
How many times did you fall ill in the last one year ? What were the illnesses ?
(a) Think of one change you could make in your habits in order to avoid any of/most of the above illnesses.
(b) Think of one change you would wish for in your surroundings in order to avoid any of/most of the above illnesses.
Answer:
I suffered last year from cough and common cold (thrice), typhoid (once), malaria (once), loose motions (thrice)
(a) Change in Habits,
- I should not sit along with those persons who are suffering from cough and cold,
- I should take care of not eating unprotected food,
- I should protect myself from mosquito bites.
(b) Change in Surroundings. Sanitary conditions in and around my home should be improved. The drains should be regularly cleaned and kept covered.
Question 2.
A doctor/nurse/health worker is exposed to more sick people than others in the community. Find out how she avoids getting sick herself. (CCE 2012, 2013, 2017)
Answer:
Through
- vaccination against most of the common diseases,
- use of gloves,
- use of different dress or coat while visiting patients, and
- use of disposable syringes and needles.
Question 3.
Conduct a survey in your neighbourhood to find what the three most common diseases are. Suggest three steps that could be taken by your local authorities to bring down the incidence of these diseases.
Answer:
The three most common diseases in my neighbourhood are malaria, typhoid and diarrhoea. The diseases mostly spread through unhygienic surroundings. The authorities should take care of
- disposal of garbage,
- cleaning of drains with occasional spray of insecticides
- covering of drains and
- providing clean drinking water.
Question 4.
A baby is not able to tell his/her caretakers that he/she is sick. What would help us to find out
(a) that the baby is sick
(b) what the sickness is ?
Answer:
- Running fever
- Cold and cough
- Excessive crying
- Loose motions
- Non-intake of proper diet.
To find the sickness, the baby is taken to a doctor. The doctor is able to diagnose the disease with the help of stethoscope, palpation (feeling with hand), above symptoms and laboratory test.
Question 5.
Under which of the following conditions is a person most likely to fall sick ?
(a) When she is recovering from malaria.
(b) When she has recovered from malaria and is taking care of someone suffering from chicken-pox ?
(c) When she is on a four day fast after recovering from malaria and is taking care of someone suffering from chicken-pox. Why ?
Answer:
(c) Four day fast will make the person weak with reduced immunity. As a result the chances of picking up chicken-pox and falling sick would be more.
Question 6.
Under which of the following conditions are you most likely to fall sick ?
(a) When you are having examinations.
(b) When you have travelled by bus and train for two days.
(c) When your friend is suffering from measles. Why ?
Answer:
(c) Measles is an infectious viral disease of young children which spreads through nasal or throat discharge (droplet method, fomite and other contacts). Visiting such a friend is likely to provide infection.
SELECTION TYPE QUESTIONS
Alternate Response Type Questions
(True/False, Right/Wrong, Yes/No)
Question 1.
Health of an individual depends on the surroundings.
Question 2.
Gainful employment has no relation to individual health.
Question 3.
On the basis of symptoms, physicians look for signs of disease.
Question 4.
High blood pressure is an infectious disease.
Question 5.
Penicillin is effective against bacteria because it inhibits their wall formation.
Question 6.
In open spaces, air borne human diseases spread rapidly.
Question 7.
AIDS spreads through sex, blood to blood contact and from mother to child.
Question 8.
Personal hygiene is basic to prevent infectious diseases.
Matching Type Questions :
Question 9.
Match the contents of the columns I and II (single matching)

Question 10.
Match the contents of columns I, II and III (double matching)

Question 11.
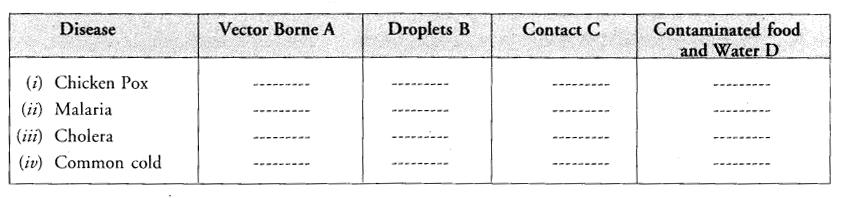
Which type of pathogen(Viral-V, Bacteria-B, Protozoan-P) cause the following discases (key or Check List Items)

Question 12.
Match the stimulus with Appropriate Response.
Fill in the Blanks
Question 13. ………….. medicines are difficult to make as the pathogens have very few biochemical mechanisms of their own.
Question 14. In AIDS patients even small cold can become ……………. .
Question 15. Sleeping sickness is caused by …………. a protozoan.
Question 16. The two important contributory causes of diseases are ……………. and …………… make up.
Question 17. Health is the state of well being physically, ……………. and socially.
Answers:
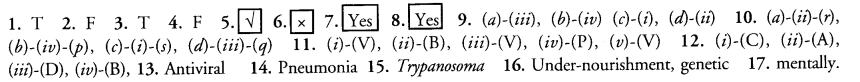
SOME TYPICAL QUESTIONS
Question 1.
Which parameters to health are difficult to measure ?
Answer:
Mental health and social well being.
Question 2.
Name the biologist who established that pathogen is a disease agent.
Answer:
Robert Koch.
Question 3.
Name the enzyme present in tears which prevents eye infections.
Answer:
Lysozyme.
Question 4.
What kills bacteria in our food in the mouth and stomach ?
Answer:
The enzyme lysozyme in saliva kills bacteria in food in our mouth, and in stomach HC1 of gastric juice kills the bacteria.
Question 5.
If a pregnant mother is suffering from AIDS, would her child get the disease via genes or placenta ?
Answer:
Placenta (Note : AIDS is not a genetic disease).
Question 6.
Why is it difficult to develop vaccines for some diseases ? (CCE 2011)
Answer:
It is difficult to develop vaccines against the diseases caused by viruses. Viruses are very specific to hosts. They have no metabolic machinery of their own. Viruses live and multiply only in the living cells. They cannot be cultured on artificial medium. It is because of these that vaccines are difficult to be prepared in such cases.
Question 7.
While going abroad, why is it essential to get vaccinated against certain diseases ?
Answer:
A person may be carrier of some disease. Such a person may take that particular disease to a foreign country. Therefore, all visitors to a foreign country are vaccinated against the disease which is not prevalent in that country.
Question 8.
Name such a vaccine which saves the life of babies from three diseases.
Answer:
D.P.T. is a vaccine which is three-in-one. Babies should be immunised within the first six weaks of birth D = Diphtheria, P= Pertussis (whooping cough), T = Tetanus.
Question 9.
Who discovered small pox vaccine ?
Answer:
Edward Jenner.
Question 10.
Define the word disease carrier.
Answer:
One who harbours germs of a disease but does not suffer from the disease is termed as carrier.
Question 11.
What are the common symptoms of infection ?
Answer:
In nearly all the infections of the human body, there is a rise in body temperature, an increased rate of heart beat, increased frequency of respiration, dry tongue, poor appetite, concentration of urine and changes in white blood cells circulating the blood.
NCERT Solutions for Class 9 Science Chapter 13 Why Do We Fall ill
Hope given NCERT Solutions for Class 9 Science Chapter 13 are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.