CBSE Class 11

By going through these CBSE Class 11 Maths Notes Chapter 16 Probability Class 11 Notes, students can recall all the concepts quickly.

Probability Notes Class 11 Maths Chapter 16

Coin, Die and Playing cards
(i) Coin : It has two sides, viz. head and tail. If we have more than one coin, coins are regarded as distinct, if not otherwise stated.

(ii) Die : A die has six faces marked 1, 2, 3, 4, 5 and 6. If we have more than one die, all dice are regarded as different, if not otherwise stated.

(iii) Playing cards : Its pack has 52 cards. There are four suits, viz., spade, heart, diamond and club, each having 13 cards. There are two colours red (heart and diamond) and black (spade and club) each having 26 cards. In 13 cards of each suit, there are 3 face cards viz. king, queen and jack. So, there are in all 12 face cards in a pack of playing cards. Also, there are 16 honour cards, 4 of each suit viz., ace, king, queen and jack.

The set of all possible outcomes of an experiment is called the sample space of that experiment. It is usually denoted by S. The elements of S are called sample points and the subset of S is called an event.

Note : Elements of sample space are known as sample points.

If an experiment conducted repeatedly under the identical conditions does not give necessarily the same result, then the experiment is called random experiment. The result of the experiment is called outcome.

Different types of events :

1. Simple event: If an event has only one sample point of the sample space, it is called a simple (or elementary) event.
2. Compound event : When an event is composed of a number of simple events, then it is called a compound event.
3. Null event: An event having no sample point is called null event. It is denoted by Φ. It is also known as impossible event.
4. Sure event: The event which is certain to occur is said to be the sure event.
5. Equally likely events : Events are called equally likely, when we do not expect the happening of one event in preference to the other.
6. Mutually exclusive events: A set of events is said to be mutually exclusive, if the happening of one event A excludes the happening of the other event B, i.e., A ∩ B = Φ
7. Exhaustive events : A set of events is said to be exhaustive, if the performance of the experiment always results in the occurrence of at least one of them.

If A is an event of an experiment whose sample space is S, then its probability P(A) is given by
P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{\text { Number of favourable cases }}{\text { Total number of exhaustive cases }}\)

P(A ∪ B) = P(A) + P(B) – P(A ∩ B), where A and B are any two events.

P(A ∪ B) = P(A) + P(B), where A and B are mutually exclusive events.

0 ≤ P(A) ≤ 1, for an event A.

P(\(\overline{\mathrm{A}}\)) = 1 – P(A), where P(\(\overline{\mathrm{A}}\)) denotes the probability of not happening the event A.

P(A ∪ \(\overline{\mathrm{A}}\)) = P(S) = 1.

If the event A implies the event B, then P(A) ≤ P(B).

P(A ∪ B ∪ C) = PC A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C).

For any two events A and B,
(i) P(A ∩ \(\overline{\mathrm{B}}\)) = P(A) – P(A ∩ B)
(ii) P(\(\overline{\mathrm{A}}\) ∩ B) = P(B) – P(A ∩ B).

Two events A and B associated with the same random experiment are independent, if and only if, P(AB) = P(A).P(B).

Let p₁ p₂, …, p_n be the probabilities of r independent events A₁ A₂,…, A_n respectively. Then, the probability that at least one of r events happen = 1 – (1 -P₁)(1 – p₂) (1 – p₃)… (1 – P_r)
= \(\frac{\text { No. of favourable cases }}{\text { No. of cases which are not favourable }}\)

Odds in favour of an event
= \(\frac{\text { No. of cases which are not favourable }}{\text { No. of cases which are favourable }}\)

By going through these CBSE Class 11 Maths Notes Chapter 15 Statistics Class 11 Notes, students can recall all the concepts quickly.

Statistics Notes Class 11 Maths Chapter 15

Before we discuss about the measure of deviations, we are expected to know how to calculate arithmetic mean \(\bar{x}\) and median.
To find mean of a distribution, we proceeded as :
For ungrouped data : x₁, x₁ …….. x_n.
\(\bar{x}=\frac{x_{1}+x_{2}+\ldots+x_{n}}{n}=\frac{\Sigma x_{i}}{n}\)

For discrete frequency distribution

For Continuous Frequency distribution : Let a be the assumed mean.
∴ d_i = x_i – a, h = class interval
and N = Total frequency = f₁ + f₂ + … f_n
Then \(\bar{x}=a+\left(\frac{\Sigma f_{i} d_{i}}{N}\right) \times h\)
To calculate the median, the process is as follows :
For ungrouped data : Arrange the data in ascending or descending order.

If n is odd, \(\left(\frac{n+1}{2}\right)\) th value = Median
If n is even \(\frac{1}{2}\left[\frac{n}{2} \text { th value }+\left(\frac{n}{2}+1\right)^{\text {th }} \text { value }\right]\) = Median
Same method is adopted in case of discrete frequency distribution.

For continuous frequency distribution:
(i) Find the cumulative frequencies :
(ii) \(\frac{\mathrm{N}}{2}\)th or next of \(\frac{\mathrm{N}}{2}\)th cumulative frequency correspond to median class.
(iii) Cumulative frequency C just before \(\frac{\mathrm{N}}{2}\)th c.f. is denoted by C.
(iv) l = lower limit of median class
h = class interval of median class
f= frequency corresponding to median class
Then, median = M = l + \(\left(\frac{\frac{N}{2}-C}{f}\right)\)x h

Measures of dispersion are required to study the degree of scattemess of observations from the central value. The central value may be mean (or median).

Mean deviation from the mean : If a set of n observations x₁ x₂, … x_n have their mean \(\bar{x}\), then mean deviation from the mean \(\bar{x}=\frac{\sum_{i=1}^{n}\left|x_{i}-\bar{x}\right|}{n}\) , where |x_i – \(\bar{x}\)| is the abosolute value of the deviation of x_i from\(\bar{x}\) .

In case, the distribution is a grouped one, the mean deviation from the mean is given by
M.D \((\bar{x})=\frac{\sum_{i=1}^{k} f_{i}\left|x_{i}-\bar{x}\right|}{\sum_{i=1}^{k} f_{i}}\)
where k is the number of classes.

Mean deviation from the median : If a set of n observations are x₁, x₂, x₃, ………….x_n, then mean deviation from the median = M.D. (Med.)
= \(\frac{\Sigma \mid x_{i}-\text { Median } \mid}{n}\)
In case of grouped data, M.D. (Med.) = \(\frac{\Sigma f_{i} \mid x_{i}-\text { Median } \mid}{\Sigma f_{i}}\)

Variance and Standard Deviation: In case of mean deviation from the mean, we take the absolute values of the deviations from the mean, so that their sum does not become zero. Another way is to find the square of the deviations and then add up. It may be possible that \(\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\) in case of distributions having large number of observations but small deviations may be larger than that in case of a distribution having small number of observations but larger deviations which may not be true. As such, to overcome this difficulty, we take average of the squares of deviations.

Thus, variance = \(\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n}\) and standard deviation = σ = \(\sqrt{\text { variance }}=\sqrt{\frac{\Sigma\left(x_{i}-\bar{x}\right)^{2}}{n}} .\)

Short-cut Method to Calculate Variance for discrete frequency distribution :

For continuous frequency distribution : Let a be the assumed mean and h be the class interval.
Now, we calculate the variable, y_i as
y_i = \(\frac{x_{i}-a}{h}\)

Comparison of variability of distribution : To compare the variability of two or more distributions, we calculate the coefficient of variation of each distribution, i.e.,
Coefficient of variance (C.V.)
= \(\frac{\text { Standard Deviation }}{\text { Mean }}\) x 100
= \(\frac{\sigma}{x}\) x 100
Greater is the value of coefficient of variation of a distribution, there is more variability in that distribution.

By going through these CBSE Class 11 Maths Notes Chapter 14 Mathematical Reasoning Class 11 Notes, students can recall all the concepts quickly.

Mathematical Reasoning Notes Class 11 Maths Chapter 14

Statement : A sentence is called mathematically acceptable statement, if it is either true of false but not both.

Negation of a Statement: The denial of a statement is called negation of the statement e.g.
If p : Diagonals of a rectangle are equal.

So, ~ p : Diagonals of a rectangle are not equal. This may also be written as
~ p : It is false that diagonals of a rectangle are equal. Further, it may also be written as
~ p : There is at least one rectangle whose diagonals are not equal.

Compound Statement: A compound statement is a statement which is made up of two or more statements.
Each statement is called a component statement.

The Connecting Word “And” : We can connect the two statements by the word “AND”, e.g. ‘
p : 48 is divisible by 4.
q : 48 is divisible by 6.
p and q : 48 is divisible by 4 and 6.

Truth Value of p and q : The statementp and q are both true, otherwise it is false, i.e., it is false, when
(i) p is true and q is false.
(ii) p is false and q is true.
(iii) p is false and q is false.

The Connecting Word “OR” : The statement p and q may be connected by the connecting word ‘OR’: i.e., p or q, e.g.
p : Ice cream is available at dinner.
q : Coffee is available at dinner.
p or q : Ice cream or coffee is available at dinner.

Exclusive “OR” : In a statement p or q, if one of the statements either p or q is true, then the statement is true. Thus, connecting of word “OR” is exclusive.

Inclusive “OR” : In a statement either both are true, then connecting word ‘OR’ is inclusive, e.g.
At plus one level, a student can either opt for Biology or Mathematics or both.
Here, the connecting word “OR” is inclusive.

Truth value of p or q : When p and q statements both are false, then p or q is also false, otherwise it is true.
Thus, p or q is true, when
(i) p is true, q is false.
(ii) p is false, q is true.
(iii.) p and q both are true.

Quantifier “There Exists” : There exists, is used for at least one e.g.
p : There exist, a quadrilateral whose all sides are equal.
The statement is equivalent to
There is at least one quadrilateral whose all sides are equal.

Quantifier “For All” : In mathematical statements “for all” is commonly used e.g. For all n ∈ N implies that each n is a natural rumber.

Implications : “If then”, “only if’ and “if and only if’ are known as imphcations. .
If p then q : The statement if “p then q” says that in the event if p is true, the i q must be true e.g.
‘ I a numbei ” a multiple of 4, then it is a multiple of 2.
Here p : A ni her is a multiple of 4.
and q : The m. aber is a multiple of 2.
When p is true i.e., a number is a multiple of 4, then q is true
i. e., the number is a multiple of 2.

“If p then q” may be used as : l.p implies q : It is denoted by p ⇒ q. The symbol ⇒ stands for implies.
2. p is sufficient condition for q : A number is a multiple of 4 is sufficient to conclude that the number is a multiple of
3. p only if q. The number is a multiple of 4 only if it is a multiple of 2.
4. q is a necessary condition for p. When the number is a multiple of 4, it is necessarily a multiple of 2.
5. – q implies ~ p (~ stands for negation or not)

Converse Statement : The converse of “if p then q” is if q then p e.g.
If a number x is odd, then x² is also odd.
Its converse is : If x² is odd, then x is also odd.

Contrapositive Statement: Contrapositive of “if p then q” is if not q then not p. e.g. contrapositive of
“If a number is divisible by 4, it is divisible by 2”, is
“If a number is not divisible by 2, then it is not divisible by 4”.

Truth Value of “If p then q” : Truth value of the statement “if p then q” is false, when p is true and q is false, otherwise it is true, ue., It is true, when
(i) p is true, q is true.
(it) p is false, q is true.
(iii) p is false, q is false.

However, three methods are adopted to test the truth value of this statement.
(1) Assuming that p is true, prove that q must be true. (Direct method).
(2) Assuming that q is false, prove thatp must be false.
(3) Assuming thatp is true and q is false, obtain a contradiction. (Contradiction method).

Statements with “If and Only If’: “If and only if’, represented by the symbol ⇔, has the following equivalent forms :
(i) p if and only if q.
(it) q if and only p.
(iii) p is necessary and sufficient condition for q and vice-verse.
(iv) p ⇔ q.

Truth Value of “If and only If” : Truth value of statements with “if and only iP is true when p and q are both true or false, otherwise it is false, ue.., statement if and only if is true, when
(i) p is true, q is true.
(ii) p is false, q is false.

Statement with if and one if is false, when
(i) p is true, q is false
(ii) p is false, q is true.

To, Prove A Statement By Contradiction
Example : To prove that √3 is irrational.
Let √3 be rational. So, √3 = p/q, where p and q are co-prime.
p² = 3q² ⇒ 3 divides p or 3 is a factor of p.
Let p = 3k. ∴p² = 9k².
∴ p² = 3q²becomes 9k² = 3q² or 3k² = q².
This means 3 is a factor or q.
i. e., 3 is a factor of p and q both. This is a contradiction.
∴ √3 is irrational.

Counter Example : To prove that a statement is false, we find an example (called counter example) by which the given statement is not valid. Then, we say that the statement is false.

By going through these CBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives Class 11 Notes, students can recall all the concepts quickly.

Limits and Derivatives Notes Class 11 Maths Chapter 13

Left Hand Limit: The \(\lim _{x \rightarrow a^{-}}\)f(x) is the expected value f(x) at x = a, given the values of fix) near x to the left of a. This value is called the left hand limit of f(x) at a.

Right Hand Limit : The \(\lim _{x \rightarrow a^{+}}\)f(x) is the expected value of f(x) at x – a, given the values of fix) near x to the right of a. ‘ ‘his value is called the right hand limit of f(x) at a.

Limit of a Function: If the right and left hand limits coincide, the common value of the limit of f(x) as x → a is called the limit of a function. It is denoted by \(\lim _{x \rightarrow a}\)f(x).

Algebra of Limits:
(i) Limit of sum of two functions is sum of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}\) [(x)+g(x)] = \(\lim _{x \rightarrow a}\)f(x) + \(\lim _{x \rightarrow a}\) g(x).

(ii) Limit of difference of two functions is difference of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}\) [(x)-g(x)] = \(\lim _{x \rightarrow a}\)f(x) – \(\lim _{x \rightarrow a}\) g(x).

(iii) Limit of product of two functions is product of the limits
of the functions i.e.,
\(\lim _{x \rightarrow a}\) [(x)+g(x)] . \(\lim _{x \rightarrow a}\)f(x) . \(\lim _{x \rightarrow a}\) g(x).

(iv) Limit of quotient of two functions is quotient of the limits of the functions (whenever the denominator is non-zero i.e..
\(\lim _{c \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}\)

(v) \(\lim _{x \rightarrow a}\) (c.f)(x) = c\(\lim _{x \rightarrow a}\)f(x)

Limit of Polynomial:
Let f(x) = a₀ + a₁x + a + a₂x² + … + a_nxⁿ be a polynomial function.
Let \(\lim _{x \rightarrow a}\) x^k = a^k.
\(\lim _{x \rightarrow a}\) f(x) = [a₀ + a₁x + a + a₂x² + … + a_nxⁿ]
= a₀ + a₁\(\lim _{x \rightarrow a}\)x + a + a₂\(\lim _{x \rightarrow a}\)x² + … + a_n\(\lim _{x \rightarrow a}\)xⁿ
= a₀ + x₁a + a₂a² + … + a_naⁿ
= f(a).

Limit of Rational Function : A function f is said to be a rational function, if f(x) = \(\frac{g(x)}{h(x)}\), where g(x) and h(x) are polynomials h(x) ≠ 0

However, ifg(a) = 0 and h(a) = 0, i.e., this is of the form 0/0 then factor(s),x-a of g(x) and h(x) are determined and then cancelled out.
Let g(x) = (x-a)p(x)
h(x) = (x-a)q(x)

(ii) For any positive integer n,
\(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}\) = na^n-1

Theorems:
(i) Let f and g be two real valued functions with the same domain such that f(x) ≤ g(x) for allx in the domain of definition. For some a, if both \(\lim _{x \rightarrow a}\)f(x) and \(\lim _{x \rightarrow a} g(x) exist, then
[latex]\lim _{x \rightarrow a}f(x) ≤ [latex]\lim _{x \rightarrow a}\)g(x)

(ii) Sandwich Theorem : Let f, g and h be real functions
such that f(x) ≤ g(x) ≤ h(x) for all x in the common domain of
definition. For some real number a, if \(\lim _{x \rightarrow a}\)g(x) f(x) = Z, \(\lim _{x \rightarrow a}\)g(x) = h(x) = l, then lim g(x) = l.

Limit of Trigonometric Functions :
(i) \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\) = 1
(ii) \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}\) = 0

Derivative of f(x) at x = a : Suppose f is a real valued of function and a is a point in its domain of definition. The derivative of f at x = a is defined by
\(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
provided this limit exists. It is denoted by f'(a).

Derivative of fix) : Suppose f is a real valued function, the function defined by \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) wherever the limit exists is defined to be the derivative of/‘and is denoted by fix). Thus,

f ‘(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

Algebra of Derivative of Functions:
(i) Derivative of sum of two functions is sum of the derivatives of functions:
\(\frac{d}{d x}\)[f(x) + g(x)] = [\(\frac{d}{d x}\)f(x) + \(\frac{d}{d x}\)g(x)]
or (u + v)’ = u’ + v’.

iii) Derivative of difference of two functions is the difference of the derivatives of the functions :
\(\frac{d}{d x}\)[f(x) – g(x)] = [\(\frac{d}{d x}\)f(x) – \(\frac{d}{d x}\)g(x)]
or (u + v)’ = u’ + v’.

(iii) Derivative of product of two functions is given by the product rule, i.e.,
or (u .v)’ = u’v + uv’.

(iv) Derivative of quotient of two functions is given by quotient rule (whenever the denominator is non-zero).

(v) Derivative of λf(x)
\(\frac{d}{d x}\)[λf(x)] = λ \(\frac{d y}{d x}\)f(x)
or (λu)’ = λu’

Some Derivatives:
(i) \(\frac{d}{d x}\)xⁿ = nxn-1
(ii) \(\frac{d}{d x}\)(ax + b)ⁿ = na(ax + b)^n-1
(iii) If f(x) = a₀xⁿ + a₁x^n-1 + a₂x^n-2 + … a_m
then na₀x^n-1 + (n-1)a₁x^n-2 + (n-2)a₂x^n-3+ …….. +a_n-1
(iv) \(\frac{d}{d x}\) (sin x) = cos x.
(v) \(\frac{d}{d x}\) (cos x) = – sin x.
(vi) \(\frac{d}{d x}\) (tan x) = sec² x.
(vii) \(\frac{d}{d x}\) (cosec x) = – cosec x cot x.
(viii) \(\frac{d}{d x}\) (sec x) = sec x tan x.
(ix) \(\frac{d}{d x}\) (cot x) = cosec² x

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 10 Cell Cycle and Cell Division. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 10 Important Extra Questions Cell Cycle and Cell Division

Cell Cycle and Cell Division Important Extra Questions Very Short Answer Type

Question 1.
Who first described meiosis?
Answer:
Strasburger,

Question 2.
What is a genome?
Answer:
It is a full set of DNA instructions or a single set of chromosomes in a cell.

Question 3.
What is meant by the non-disjunction of chromosomes?
Answer:
Non-disjunction means failure in the separation of homologous chromosomes during anaphase.

Question 4.
Why is mitosis an equational division?
Answer:
Mitosis is an equational division because the daughter cells get the same number of chromosomes from the parent.

Question 5.
What is crossing over?
Answer:
The exchange of segments of chromatids of homologous chromosomes during meiosis is called crossing over.

Question 6.
Why is meiosis a reductional division?
Answer:
Meiosis is a reductional division because it reduces the number of chromosomes from diploid number to haploid number in the daughter cells.

Question 7.
What are the two successive divisions in meiosis?
Answer:
The first division is reductional followed by the second equational di¬vision.

Question 8.
Name the two phases of the cell cycle of a somatic cell.
Answer:

1. Interphase and
2. M-phase or mitotic phase

Question 9.
During which part of interphase active synthesis of RNA and proteins take place.
Answer:
G. phase.

Question 10.
What amount of DNA is present in the cell during the G₂ phase?
Answer:
Double the amount of DNA present in the original diploid cell.

Question 11.
What is a kinetochore?
Answer:
A part of the chromosome for the attachment of chromosomal fibers.

Question 12.
Define Eumitosis.
Answer:
Chromosomes are attached to the spindle by their centromere and this type of mitosis is called Eumitosis.

Question 13.
Who gave the term mitosis?
Answer:
W. Flemming.

Question 14.
How many mitotic divisions will be required to produce 128 daughter cells from a single cell?
Answer:
127.

Question 15.
What is the Gj phase of the interphase?
Answer:
It is the first period of growth of the neatly formed undivided cells, during which the cell synthesizes a lot of RNA and proteins.

Cell Cycle and Cell Division Important Extra Questions Short Answer Type

Question 1.
Define cell cycles.
Answer:
The cell cycle is the sequence of events that occur between the formation of a cell and its division into daughter cells.

Question 2.
What do you understand by homologous chromosomes?
Answer:
Homologous chromosomes are pairs of chromosomes that have similar characteristics. They show pairing during meiosis. One chromosome in each pair is inherited from the father and the other one from the mother.

Question 3.
Why is mitosis an equational division?
Answer:
Mitosis is an equational division because the daughter cells have the same number of chromosomes and an equal amount of cytoplasm.

Question 4.
Why is meiosis necessary in sexually reproducing organisms?
Answer:
Meiosis is necessary for sexually reproducing organisms because

1. It maintains the number of chromosomes constant in generation as meiosis is reductional division.
2. It causes variations among the progeny because crossing over takes place during meiosis. This variation is important for evolution.

Question 5.
What is the importance of mitosis?
Answer:
Mitosis is important because

1. It maintains genetic stability through generations.
2. It helps in the growth of multicellular organisms.
3. Many plants and animals multiply by mitosis i.e., asexual repro-duction to regenerate the whole organism.
4. It helps to regenerate lost parts of an animal’s body.
5. It helps in the regeneration of new cells in place of dead and worn-out cells.

Question 6.
What are homologous chromosomes? What happens to homologs during meiosis?
Answer:
Each diploid nucleus has pairs of similar chromosomes called homologous chromosomes. The two homologous chromosomes each derived from one parent during sexual reproduction come together and form pairs during the zygonema of meiosis I. Individuals of a pair are similar in length and in the position of their centromere.

Question 7.
What is the significance of meiosis?
Answer:
Significance of meiosis:

1. Sexual reproduction: Maintains a number of chromosomes constant. Characteristic of a species from generation to generation.
2. Genetic variation: Through crossing over, it produces variations of genetic characters of the progeny essential for evolution.

Question 8.
What do you mean by cell reproduction?
Answer:
Cell reproduction: Reproduction is an essential phenomenon in the continuity of life. New cells arise by the division of the pre-existing cells. It was proposed by Rudolf Virchow.

Reproduction is of two types:

1. sexual and
2. asexual reproduction.

The growth and development of the living being are dependent on the division of cells. The single-celled zygotes by means of cell division develop into an adult having a large number of cells.

Question 9.
What is P-oxidation?
Answer:
Fats are broken down into glycerol and fatty acids during digestion. Glycerol enters the glycolytic pathway at the triose phosphate stage. Fatty acids undergo β oxidation by which two-carbon fragments of acetyl A are split off at a time from the fatty acid chain so that the long fatty acid molecule is shortened by two carbon-carbon atoms at a time. This ultimately results in incomplete oxidation of fatty acids.

Question 10.
Distinguish between Anaphase of mitosis and Anaphase of meiosis I.
Answer:

Question 11.
Distinguish between combustion and respiration
Answer:

Question 12.
Distinguish between mitosis and meiosis.
Answer:

Cell Cycle and Cell Division Important Extra Questions Long Answer Type

Question 1.
Describe the changes that take place during the prophase and metaphase of mitosis.
Answer:
Following changes take place during prophase

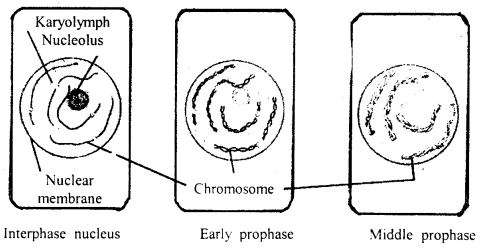
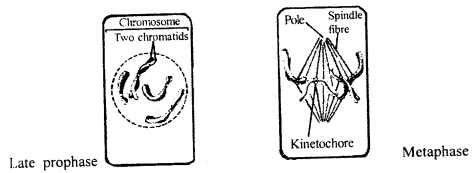
1. Chromosomes become short and thick and sister chromatids are held at the centromere.
2. Nucleus and nuclear envelope disappear.
3. In animal cells, centrioles move to opposite poles.
4. Chromosomes begin to move towards the equatorial plane.

Following changes take place in metaphase:

• Chromosomes lie on the equatorial plate.
• Chromatids become attached by spindle fibers.
• Maximum condensation of chromosomes takes place.

Question 2.
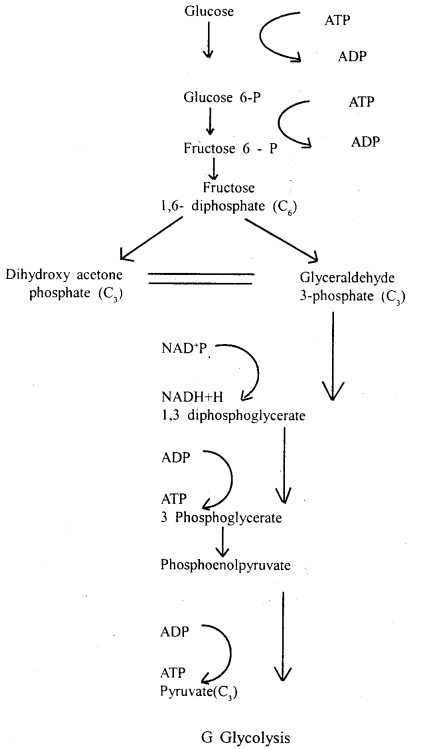
Explain the main steps in aerobic glycolysis.
Answer:
Glycolysis is the breakdown of glucose to pyruvic acid, which includes the following:
(a) Phosphorylation: Transfer of phosphate from ATP to glucose to form glucose – 6 phosphate. One molecule of ATP is consumed enzyme, hexokinase is present.

(b) Isomerisation: There is internal molecular rearrangement to form fructose 6 phosphates. The enzyme is hexose phosphate isomerase.

(c) Second phosphorylation: The fructose – 6-phosphate undergoes phosphorylation to form fructose 1,6 diphosphate. One molecule of ATP is consumed. The enzyme is phosphofructokinase.

(d) Triose phosphates are 3-phosphoglyceraldehyde (PGAL) and dihydroxyacetone phosphate (DHAP). The enzyme phosphorize isomerase maintains the two isomers in equilibrium.

(e) Phosphorylation and oxidative dehydrogenation: PGAL under¬goes simultaneous phosphorylation and oxidative dehydrogenation to form 1,3 diphosphoglyceric acid.

(f) ATP generation: 1,3 diphosphoglyceric acid transfers its phosphate with a high energy bond to ADP to form ATP and 3-phosphoric acid. One molecule of ATP is produced from one triose molecule.

One enzyme is phosphoglyceric kinase Glucose

Question 3.
How cytokinesis is different in an animal and a plant cell?
Answer:
Cytokinesis in plant and animal cells: The separation of daughter nuclei and cytokinesis or cell cleavage maybe two different processes. The first visible changes consist of an appearance of dense material around the microtubules at the equator of the spindle at either mid or late phase then although spindle the fibre tends to disorganize and disappear during telophase, they usually persist and may even increase in number at the equator, frequently intermingled with a row of vesicles and the dense material.

The entire structure is called the midbody. Simultaneously there is a depression on the cell surface a kind of constriction that deepens gradually until reaching the midbody with the completion of the furrowing, the separation of cells is concluded.

The phragmoplast begins to form in the mid anaphase of plant cells. Under the electron microscope, it is possible to observe that the vesicles are of dense material applied together to their surface. The vesicles are derived from Golgi complexes which are found in the regions adjacent to phrag¬moplast which migrate to the equatorial region to be clustered around the microtubules.

Although phragmoplast is initially found as a ring on the periphery of the cell, with time it grows centripetally by the addition of microtubules and partition until it extends across the entire equatorial plane. The vesicles increase in size and just until the two cells are separated by a fairly continuous plasma membrane.

All this time the phragmoplast has been transformed into, cell plate. Thin cytoplasmic connection is plasmoids- data transverse the cell plate and remain in place for communication between the adjacent daughter cells.

The formation of the cell plate also leads to the synthesis of the cell wall. The Golgi-vesicles in phragmoplast is already filled with secretory material consisting mainly of the pectin. The fusion of vesicles results in the combining of the pectin in the extracellular space between the two daughter cells thereby forming the main body of the periphery cell wall.