By going through these CBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives Class 11 Notes, students can recall all the concepts quickly.
Limits and Derivatives Notes Class 11 Maths Chapter 13
Left Hand Limit: The \(\lim _{x \rightarrow a^{-}}\)f(x) is the expected value f(x) at x = a, given the values of fix) near x to the left of a. This value is called the left hand limit of f(x) at a.
Right Hand Limit : The \(\lim _{x \rightarrow a^{+}}\)f(x) is the expected value of f(x) at x – a, given the values of fix) near x to the right of a. ‘ ‘his value is called the right hand limit of f(x) at a.
Limit of a Function: If the right and left hand limits coincide, the common value of the limit of f(x) as x → a is called the limit of a function. It is denoted by \(\lim _{x \rightarrow a}\)f(x).
Algebra of Limits:
(i) Limit of sum of two functions is sum of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}\) [(x)+g(x)] = \(\lim _{x \rightarrow a}\)f(x) + \(\lim _{x \rightarrow a}\) g(x).
(ii) Limit of difference of two functions is difference of the limits of the functions, i.e.,
\(\lim _{x \rightarrow a}\) [(x)-g(x)] = \(\lim _{x \rightarrow a}\)f(x) – \(\lim _{x \rightarrow a}\) g(x).
(iii) Limit of product of two functions is product of the limits
of the functions i.e.,
\(\lim _{x \rightarrow a}\) [(x)+g(x)] . \(\lim _{x \rightarrow a}\)f(x) . \(\lim _{x \rightarrow a}\) g(x).
(iv) Limit of quotient of two functions is quotient of the limits of the functions (whenever the denominator is non-zero i.e..
\(\lim _{c \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}\)
(v) \(\lim _{x \rightarrow a}\) (c.f)(x) = c\(\lim _{x \rightarrow a}\)f(x)
Limit of Polynomial:
Let f(x) = a0 + a1x + a + a2x2 + … + anxn be a polynomial function.
Let \(\lim _{x \rightarrow a}\) xk = ak.
\(\lim _{x \rightarrow a}\) f(x) = [a0 + a1x + a + a2x2 + … + anxn]
= a0 + a1\(\lim _{x \rightarrow a}\)x + a + a2\(\lim _{x \rightarrow a}\)x2 + … + an\(\lim _{x \rightarrow a}\)xn
= a0 + x1a + a2a2 + … + anan
= f(a).
Limit of Rational Function : A function f is said to be a rational function, if f(x) = \(\frac{g(x)}{h(x)}\), where g(x) and h(x) are polynomials h(x) ≠ 0
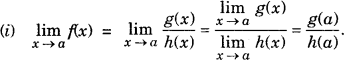
However, ifg(a) = 0 and h(a) = 0, i.e., this is of the form 0/0 then factor(s),x-a of g(x) and h(x) are determined and then cancelled out.
Let g(x) = (x-a)p(x)
h(x) = (x-a)q(x)
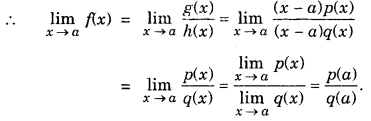
(ii) For any positive integer n,
\(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}\) = nan-1
Theorems:
(i) Let f and g be two real valued functions with the same domain such that f(x) ≤ g(x) for allx in the domain of definition. For some a, if both \(\lim _{x \rightarrow a}\)f(x) and \(\lim _{x \rightarrow a} g(x) exist, then
[latex]\lim _{x \rightarrow a}f(x) ≤ [latex]\lim _{x \rightarrow a}\)g(x)
(ii) Sandwich Theorem : Let f, g and h be real functions
such that f(x) ≤ g(x) ≤ h(x) for all x in the common domain of
definition. For some real number a, if \(\lim _{x \rightarrow a}\)g(x) f(x) = Z, \(\lim _{x \rightarrow a}\)g(x) = h(x) = l, then lim g(x) = l.
Limit of Trigonometric Functions :
(i) \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\) = 1
(ii) \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}\) = 0
Derivative of f(x) at x = a : Suppose f is a real valued of function and a is a point in its domain of definition. The derivative of f at x = a is defined by
\(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
provided this limit exists. It is denoted by f'(a).
Derivative of fix) : Suppose f is a real valued function, the function defined by \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) wherever the limit exists is defined to be the derivative of/‘and is denoted by fix). Thus,
f ‘(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
Algebra of Derivative of Functions:
(i) Derivative of sum of two functions is sum of the derivatives of functions:
\(\frac{d}{d x}\)[f(x) + g(x)] = [\(\frac{d}{d x}\)f(x) + \(\frac{d}{d x}\)g(x)]
or (u + v)’ = u’ + v’.
iii) Derivative of difference of two functions is the difference of the derivatives of the functions :
\(\frac{d}{d x}\)[f(x) – g(x)] = [\(\frac{d}{d x}\)f(x) – \(\frac{d}{d x}\)g(x)]
or (u + v)’ = u’ + v’.
(iii) Derivative of product of two functions is given by the product rule, i.e.,
or (u .v)’ = u’v + uv’.
(iv) Derivative of quotient of two functions is given by quotient rule (whenever the denominator is non-zero).
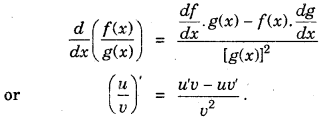
(v) Derivative of λf(x)
\(\frac{d}{d x}\)[λf(x)] = λ \(\frac{d y}{d x}\)f(x)
or (λu)’ = λu’
Some Derivatives:
(i) \(\frac{d}{d x}\)xn = nxn-1
(ii) \(\frac{d}{d x}\)(ax + b)n = na(ax + b)n-1
(iii) If f(x) = a0xn + a1xn-1 + a2xn-2 + … am
then na0xn-1 + (n-1)a1xn-2 + (n-2)a2xn-3+ …….. +an-1
(iv) \(\frac{d}{d x}\) (sin x) = cos x.
(v) \(\frac{d}{d x}\) (cos x) = – sin x.
(vi) \(\frac{d}{d x}\) (tan x) = sec2 x.
(vii) \(\frac{d}{d x}\) (cosec x) = – cosec x cot x.
(viii) \(\frac{d}{d x}\) (sec x) = sec x tan x.
(ix) \(\frac{d}{d x}\) (cot x) = cosec2 x