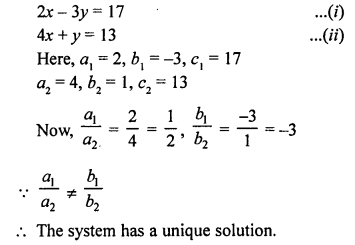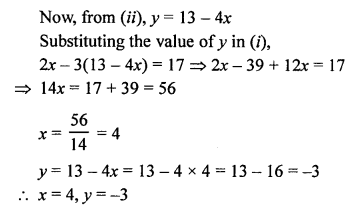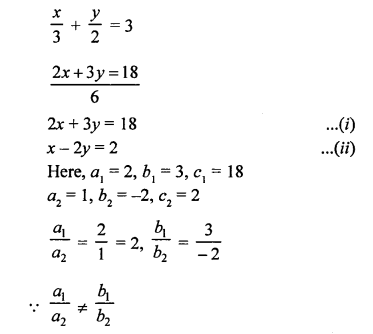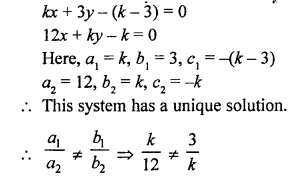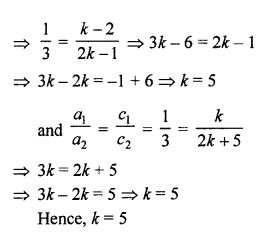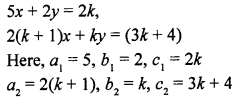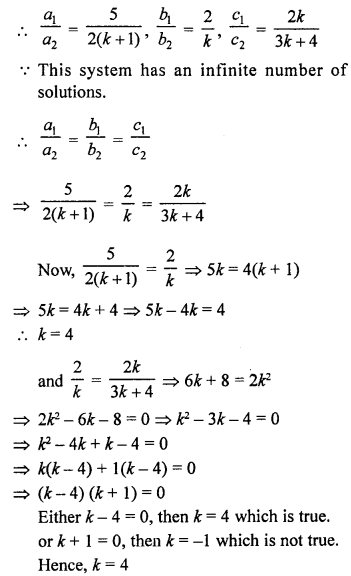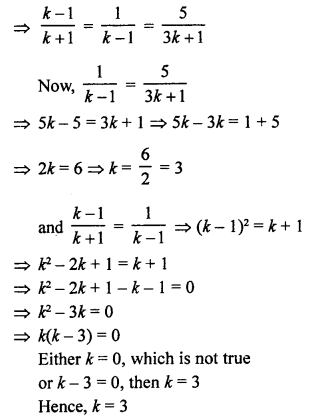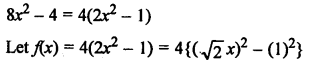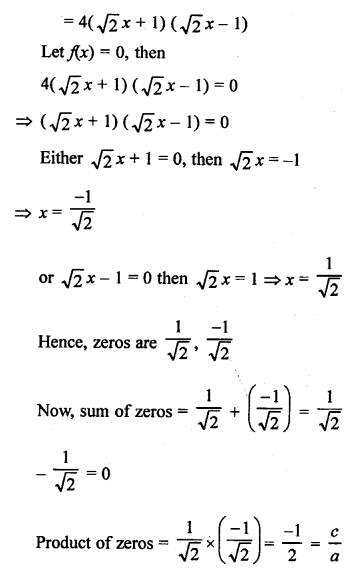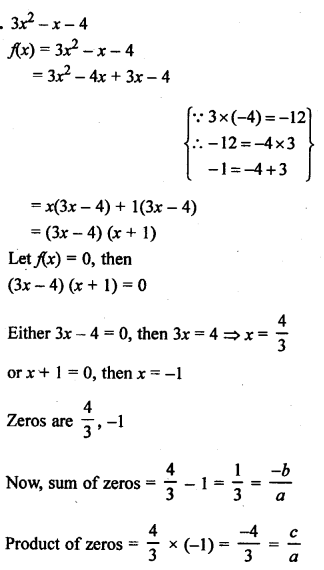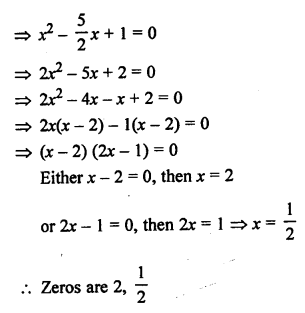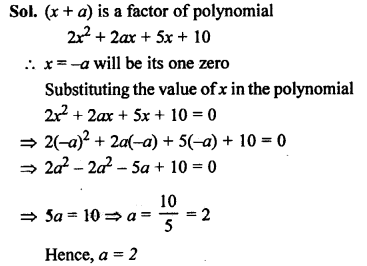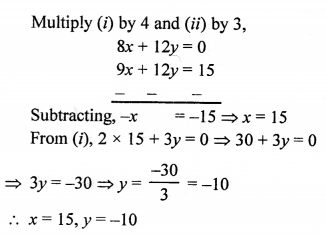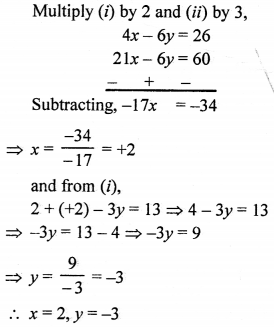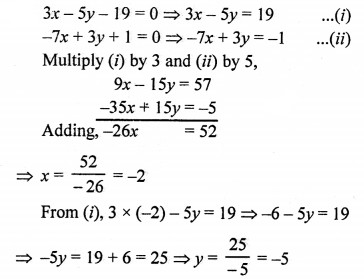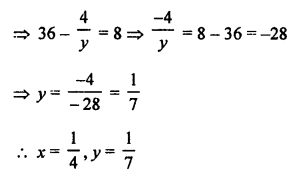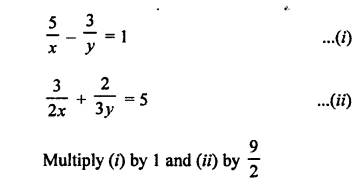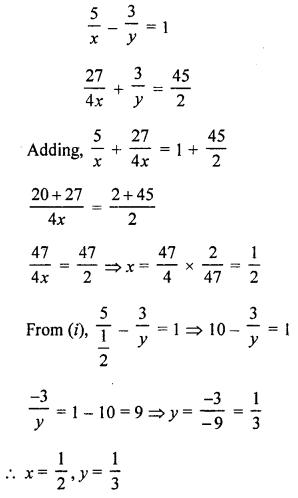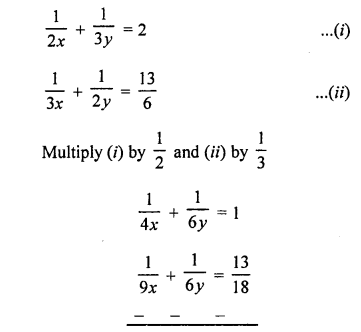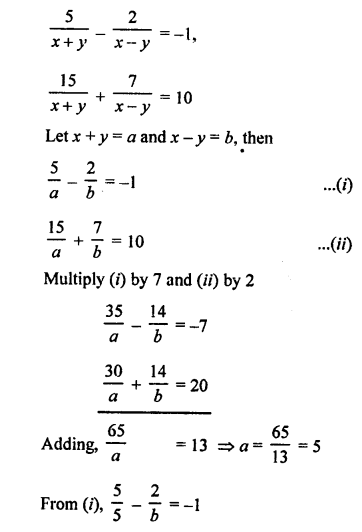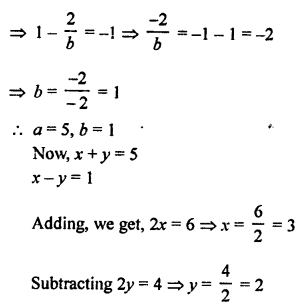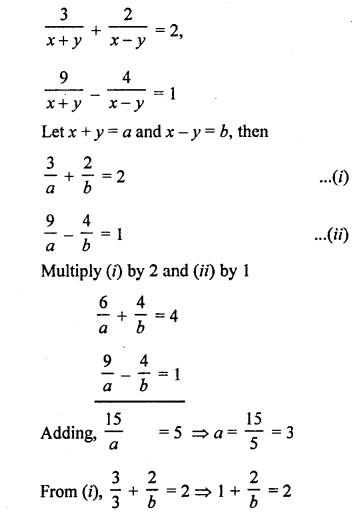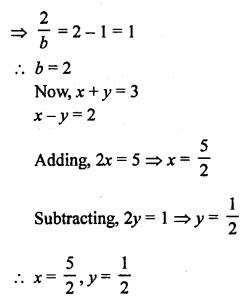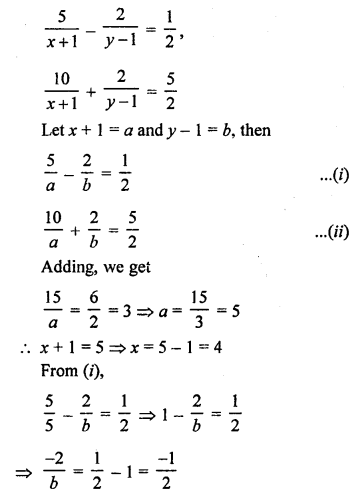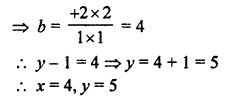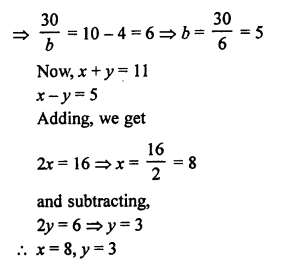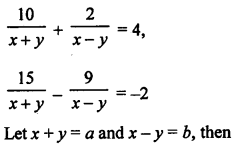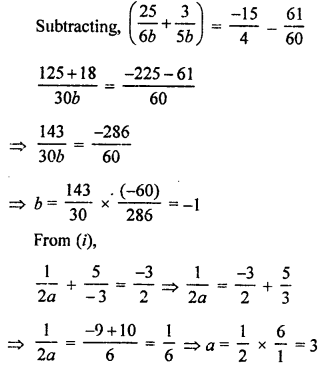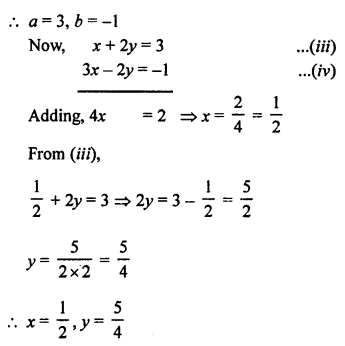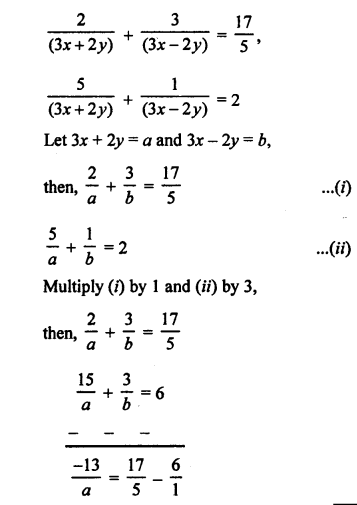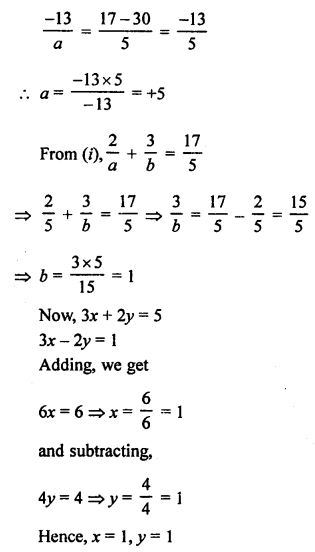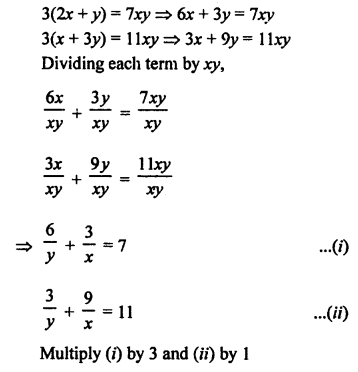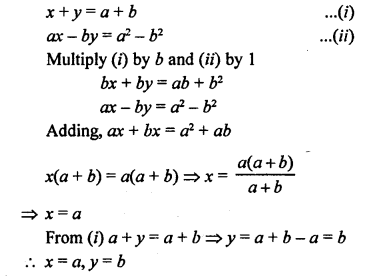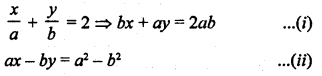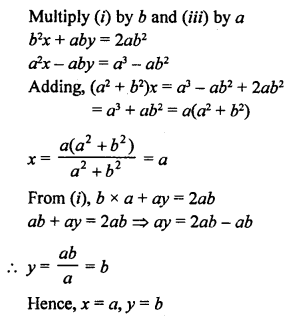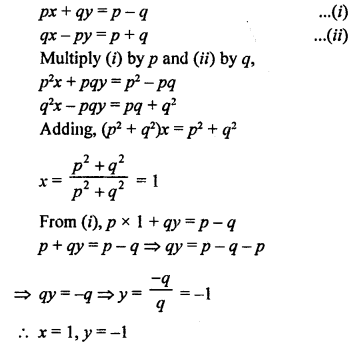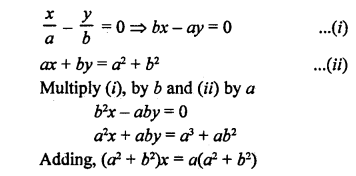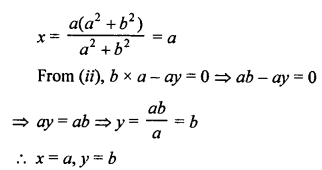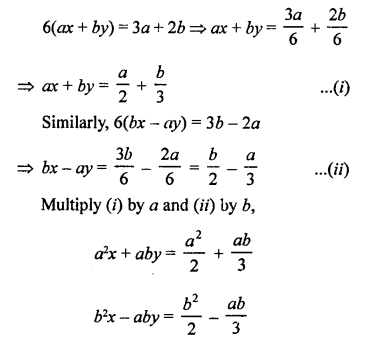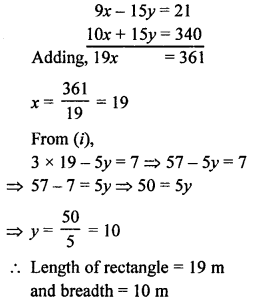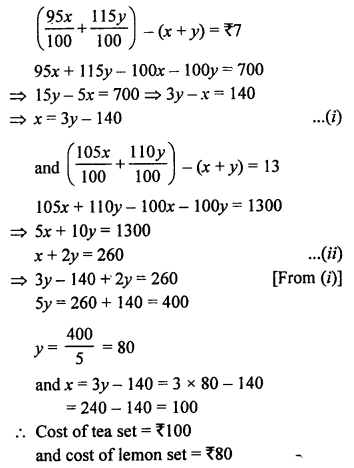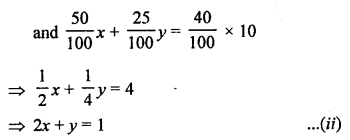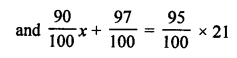Here we are providing Patol Babu, Film Star Extra Questions and Answers Class 10 English Literature Reader, Extra Questions for Class 10 English was designed by subject expert teachers.
Patol Babu, Film Star Extra Questions and Answers Class 10 English Literature
Patol Babu, Film Star Extra Questions and Answers Short Answer Type
Question 1.
Who was Naresh Dutt?
Answer:
Naresh Dutt worked in the film business, he was the youngest brother-in-law of Nishikanto Ghosh, who was Patol Babu’s neighbour.
Question 2.
While buying vegetables at the market, Patol Babu mixed up the order. What does this tell you about his state of mind? Why did this happen?
Answer:
It shows that Patol Babu was very excited at the prospect of getting an opportunity to work in a film. In fact at one time, he used to perform on the stage in his neighbourhood and had been quite good at it.
Question 3.
Do you think Patol Babu was happy with his career? Give reasons for your answer.
Answer:
No, because Patol Babu had changed his jobs and career choices a number of times and really struggled to make a living without managing to improve his lot.
Question 4.
Did Patol Babu miss his acting days? Give reasons for your answers.
Answer:
Yes, he did. Patol Babu could still remember lines from some of the roles he had played in the past.
Question 5.
Why had Patol Babu given up hope at half past twelve?
Answer:
Patol Babu had given up hope because he had been told that Naresh Dutt, the man who was to offer him a role in the movie would be coming at 10:30 a.m.
Question 6.
What instructions does Naresh Dutt give Patol Babu on their first meeting?
Answer:
Naresh Dutt told him to report for shooting the next morning at 8:30 a.m. He also told him that the shooting would take place out of doors, outside the front entrance of a seven-storey office building called Faraday House.
Question 7.
What was the role that was offered to Patol Babu?
Answer:
Patol Babu was to enact the role of an absent-minded, short-tempered pedestrian.
Question 8.
Why was Patol Babu asked to wear a woollen jacket?
Answer:
Patol Babu was asked to do so because the story was supposed to take place in winter.
Question 9.
How did Patol Babu’s wife react to the news?
Answer:
Patol Babu’s wife was sceptical and asked him not to count his chickens before they hatched.
Question 10.
Why did Patol Babu feel humiliated when he reported for the shoot?
Answer:
When Patol Babu saw the single word written on the paper as a dialogue, he felt that the people were pulling his leg and everything was a hoax.
Question 11.
How was Patol Babu’s role crucial to the film, according to the young man Jyoti?
Answer:
According to Jyoti, Patol Babu’s role was crucial because the interaction with Patol Babu would show the preoccupation of the hero with his problem.
Question 12.
Was Patol Babu impressed with his dialogue? Give reasons for your answer.
Answer:
No, Patol Babu was not impressed with his dialogue because he felt the people were pulling his leg when he looked at his dialogue.
Question 13.
While waiting for his shot, Patol Babu remains deep in thought? What was the thought?
Answer:
Patol Babu started thinking of the manner in which he usually spent his Sunday at Karali Babu’s house listening to songs sung in praise of Goddess Kali. He started wondering whether he could quietly slip away.
Question 14.
What worried Patol Babu about his moustache?
Answer:
Patol Babu was worried that it might come off at the time he was to collide with the hero.
Question 15.
Why does’Sosanko call Patol Babu lucky?
Answer:
Patol Babu was disappointed on receiving a one-word dialogue when Sosanko explains that he was lucky to have something to say because there had been more than a hundred people who had appeared in the film and yet had nothing to say. Even the hero had no words to say on that day.
Question 16.
What feelings did Patol Babu plan to convey through his dialogue?
Answer:
Patol Babu had planned to express 60 percent irritation and 40 percent surprise through his one- word dialogue.
Question 17.
What were Patol Babu’s feelings about the people associated with film-making after the shot is over?
Answer:
Patol Babu wondered whether those people had the depth to realise the perfection with which he had just performed.
18.
Why didn’t Patol Babu stop to take his money even though he needed it badly?
Answer:
Patol Babu was so deeply satisfied with his performance that he did not feel the need to take money for it.
Patol Babu, Film Star Extra Questions and Answers Long Answer Type
Question 1.
Describe the character of Patol Babu.
Answer:
Patol Babu was a very punctual man. He was unassuming and modest and was very thrilled at learning of the opportunity in acting. He had been a talented actor in the past and people had bought tickets to see him act. He is also practical and decides to make the most of a tiny film role and practises hard. He is diligent and hard working. He is a creative person and does not wait to be paid because of the creative satisfaction that he derived from enacting the small scene.
Question 2.
Write a letter from Patol Babu to Nishikanto Ghosh describing his satisfaction with the role.
Answer:
15 May xxxx
Dear Nishikanto,
I would like to express my gratitude for recommending me to Naresh Dutt for the role. It was an opportunity of a lifetime for me as it revived memories of my youth. Now life is full of struggle and so there is no time to indulge in my passion for acting. Though the role had been small and the dialogue consisted of only one word, it was a very satisfying moment for me. After several years I felt deep contentment and joy. I hope more such opportunities come my way.
Regards
Patol
Question 3.
Write Baren Mullick’s diary for the day of the shooting.
Answer:
15 May xxxx
It was a good day as the shooting took place as per schedule. The scene required the hero to enter his office in a preoccupied state due to an incident of embezzlement in office. He bumps against a pedestrian. Incidentally the man who played the role was a surprise as he gave just the right expression. His moustache added to the overall effect. He seemed ordinary and I had doubts when I first saw him. But what a surprise package he turned out to be! His suggestion of using a newspaper added to the role. May be we could give him a bigger role in the next film.
Question 4.
Write a letter from Naresh Dutt to Patol Babu sending him the money he had earned.
Answer:
15 May xxxx
Dear Patol Babu,
Thank you for your performance today. It was excellent. The director and other members of production team were very happy with the shot. You gave just the right expression and looked the part with the jacket and moustache. The idea of using a newspaper was brilliant. But, why did you leave without taking the money? I am sending you a cheque with the letter.
Regards
Naresh Dutt
Question 5.
A film critic reviews the movie once it finally releases. Write a review, noticing the impact of Patol Babu’s scene.
Answer:
The new film by Baren Mullick is an unusual story about the struggle of an ordinary man. There is embezzlement at work, but he faces the difficulties with fortitude. The film is a testimony of great direction. The director has an eye for detail. The characters are appropriately represented and the actors.are well chosen. In fact mention must be made of the character of a pedestrian. He is an old man wearing a jacket who collides with the hero. Although, the scene lasted for a few seconds, that man managed to leave a lasting impression.
Question 6.
As Gogon Pakrashi, write a letter to Patol Babu congratulating him on his performance.
Answer:
21 May xxxx Dear Patol,
I heard of your movie debut. Well done! I always knew you would join films someday. It would be a happy moment to see your name on billboards. You had a significant impact in spite of the tiny role. Your expression after the collision was marvellous. Did you get any new offers? Please do take acting seriously.
Such talent should not be wasted. Let us meet soon.
Regards
Gogon Pakrashi
Question 7.
What is the theme of the story?
Answer:
The story is about Patol Babu’s passion for acting. For him the satisfaction derived from a good performance is enough. He had acted for his passion not for money. At one time Patol Babu had acted in the Jatras and been a favourite with the public. He hankered after a career in % films. One day, however, an opportunity to act in a film does come Patol Babu’s way.
The role that he is offered is of an ‘angry pedestrian’ who runs into the hurrying lead actor on a busy road and exclaims “Oh!” Initially, he is rather disappointed, but then he remembers the advice of his mentor that no role, no dialogue is too small for a real actor and one must perform the role whole-heartedly and to the best of ability. He rehearses the single word with different inflections to show pain, sorrow, joy, surprise, agony etc. Having performed his role he feels pride in his performance and comes home, a contented man, even without bothering to wait for his payment.
Patol Babu, Film Star Extra Questions and Answers Reference to Context
Question 1.
“I hope the part calls for some dialogue. ”
(a) Who says this?
Answer:
Patol Babu speaks these lines.
(b) To whom is he speaking?
Answer:
Patol Babu is speaking to Naresh Dutt.
(c) Why does she ask this question?
Answer:
Patol Babu had been offered a role in a movie so he wanted to know whether he had any dialogue. He had been an amateur actor in the past. His interest in acting had been rekindled.
Question 2.
“hope you won’t turn him away. They ’ll pay you, of course. ”
(a) Who is speaking? To whom is he speaking?
Answer:
Nishikanto Babu is speaking to Patol Babu.
(b) Who is he referring to?
Answer:
Nishikanto Babu is referring to his youngest brother-in-law Naresh Dutt.
(c) What would they pay the listener for?
Answer:
They would pay him for enacting a small role in their movie.
Question 3.
“He’s about thirty. A strapping young fellow. He said he would be here by ten thirty. ”
(a) Who does ‘he’ in these lines refer to? Who is the speaker?
Answer:
‘He’ refers to Naresh Dutt. Nishikanto Babu, Patol Babu’s neighbour, is the speaker.
(b) What time does he actually arrive by? Why does he come there?
Answer:
He came at half past twelve. He wanted to offer Patol Babu a role in a movie he was working in.
(c) Is his visit successful? Explain.
Answer:
Yes, because Patol Babu agrees to play the minor role of a pedestrian in the film he was associated with.
Question 4.
“Indeed there was a time when people bought tickets especially to see him. ”
(a) Who is being talked about in these lines?
Answer:
The person being talked about is Patol Babu.
(b) Why did people buy tickets to see him?
Answer:
Patol Babu had been a popular actor on stage, performing in amateur theatre, in his youth.
(c) Where was he living at that time?
Answer:
Patol Babu was living at Kanchrapara.
Question 5.
“Ever since then Patol Babu had struggled to make a living. ”
(a) What was Patol Babu’s first job?
Answer:
Patol Babu worked in a railway factory in Kanchrapara.
(b) Why did Patol Babu come to Calcutta?
Answer:
Patol Babu came to Calcutta as he was offered a higher pay in a clerical post with Hudson & Kimberley in Calcutta.
(c) Why did he have to struggle to make a living?
Answer:
Patol Babu lost his job at Kimberley & Hudson during the war years and since then had changed several jobs but could not succeed in making a living.
Question 6.
“There’s no doubt about that. By the way, the shooting takes place tomorrow morning. ”
(a) Who is the speaker? Who is he talking to?
Answer:
Naresh Dutt is speaking to Patol Babu.
(b) What is he so sure about?
Answer:
Naresh Dutt is sure about the fact that Patol Babu was just right for the role in the movie.
(c) Where was the shooting going to take place?
Answer:
The shooting was going to take place outside a seven-storey office building called Faraday House, near the crossing of Bentinck Street and Mission Row.
Question 7.
“But you haven’t told me about the part.”
(a) Who is the speaker? Who is he speaking to?
Answer:
The speaker is Patol Babu. He is speaking to Naresh Dutt.
(b) What does the ‘part’ mentioned in this line refer to?
Answer:
It refers to the movie role that had been offered to Patol Babu by Naresh Dutt.
(c) Describe the ‘part’ mentioned in this line.
Answer:
It was the role of a short-tempered, absent-minded old pedestrian who collides with the hero of the movie in a street.
Question 8.
“Fine. I wouldn ’t have come to you for just a walk on part. For that we pick people from the street. Of course there’s dialogue and you ’ll be given your lines as soon as you show up tomorrow. ”
(a) Who is the speaker? Who is being spoken to?
Answer:
The speaker is Naresh Dutt. He is speaking to Patol Babu.
(b) What was the part offered to the listener?
Answer:
Patol Babu had to enact the role of an absent-minded, short-tempered pedestrian who collides with the hero.
(c) What was the dialogue that he had to say?
Answer:
Patol Babu’s dialogue consisted of a single word, “Oh!”
Question 9.
“Counting your chickens again before they’re hatched, are you?”
(a) Who is the speaker?
Answer:
The speaker is Patol Babu’s wife.
(b) What does she mean by ‘counting your chickens before they are hatched’?
Answer:
Patol Babu had already started anticipating a career in the movies after he enacted the small role that had been offered to him. His wife made this remark cautioning him that he was talking of success before he had achieved it.
(c) What is the speaker’s opinion of the person being spoken to?
Answer:
His wife did not have a high opinion of his abilities and did not consider him a successful person.
Question 10.
“Patol Babu suddenly felt a little nervous. Should he ask somebody? There was Naresh Dutt there, should he go and remind him?”
(a) Where was Patol Babu standing at this time?
Answer:
Patol Babu was standing near the shooting site waiting for the shooting to start.
(b) Who was Naresh Dutt?
Answer:
Naresh Dutt was the youngest brother-in-law of his neighbour who had got him a role in a movie.
(c) What did he want to remind him of?
Answer:
Patol Babu wanted to remind him of the fact that he had not been given his dialogues.
Question 11.
Patol Babu now turned to his neighbour and asked in a whisper “Who is the director? ”
(a) Where was Patol Babu standing at this moment?
Answer:
Patol Babu was standing outside Faraday House waiting for his turn to enact this role.
(b) Who was the director of the movie?
Answer:
He was the famous director, Baren Mullick.
(c) Who was the hero of the movie?
Answer:
The hero was the famous actor, Chanchal Kumar.
Question 12.
“The youngster Jyoti produced a red-dot pen from his pocket and gave it to Sosanko. Sosanko tore off a page from the notebook he was carrying, scribbled something and handed it to Patol Babu. ”
(a) Who were Jyoti and Sosanko?
Answer:
They were young boys, members of the production team who were shooting a movie.
(b) What did Sosanko scribble on the paper?
Answer:
Sosanko wrote the word ‘Oh! ’
(c) Why did he give the paper to Patol Babu?
Answer:
Sosanko gave it to Patol Babu as it was the dialogue he had to say while enacting the role he had to play.
Question 13.
‘Why waste a Sunday morning in the company of these useless people, and be made to look foolish on top of that? ’
(a) Who is the speaker?
Answer:
Patol Babu is the speaker.
(b) Who are the people referred to as “useless”?
Answer:
The people making the movie are referred to as “useless”.
(c) Why is the person upset?
Answer:
Patol Babu is upset with his dialogue which consisted of just one word.
Question 14.
“Remember one thing Patol, however small a part you ‘re offered, never consider it beneath your dignity to accept it.”
(a) Who is the speaker?
Answer:
The speaker is Gogon Parkashi, Patol Babu’s mentor.
(b) Why is Patol reminded of him?
Answer:
Patol was upset with his one word dialogue, but then he remembered what his mentor had told him.
(c) How does the advice help him?
Answer:
It motivates Patol Babu to enact the one word dialogue with such emotion that even the famous director was impressed.
Question 15.
“Strange! Patol Babu suddenly felt that he could write a whole thesis on that one monosyllabic exclamation! ’
(a) What was the monosyllabic exclamation?
Answer:
It was the word, “Oh!”
(b) What makes Patol Babu feel that he could write a thesis on it?
Answer:
Patol Babu suddenly realised that the same exclamation when spoken in different ways carved different shades of meaning.
(c) How does his discovery impact his acting?
Answer:
Patol Babu puts in so much feeling in the way he utters the word that the director is impressed with him.
Question 16.
“That’s all right. I’ll certainly wait. I’ll be in that side street across the road. ”
(a) Who is the speaker? Who is being spoken to?
Answer:
Patol Babu is speaking to one of the young assistants helping in the shooting.
(b) How is this statement different from his earlier one?
Answer:
Here Patol Babu has made up his mind to put in all he has in his performance while earlier he had been tempted to slip away quietly.
(c) How did he spend his time in the side street?
Answer:
Patol Babu rehearsed his line in front of a glass window.
Question 17.
“There’s a large patch of cloud approaching the sun ”, he said. “This scene must be shot in sunlight. ”
(a) Who is the speaker?
Answer:
The speaker is Bhren Mullick, the director.
(b) Why does he make this statement?
Answer:
He makes it in reply to Patol Babu’s request for a rehearsal before the final take.
(c) Does this refusal affect Patol Babu’s performance? Give reasons for your answer.
Answer:
No, because he gives such a perfect performance that everyone is impressed including the director.
Question 18.
“I hope Grandpa wasn’t hurt too badly. ”
(a) Who says this? Who is he referring to?
Answer:
Jyoti says this line. Jyoti is referring to Patol Babu.
(b) Why does he make this remark?
Answer:
Jyoti made this remark because Patol Babu had just given a shot in which he had to collide with the lead actor and the shot had been very realistic.
(c) What was Patol Babu doing there?
Answer:
Patol Babu was performing the role of a pedestrian who collides with the hero of the movie.
Question 19.
“That’s odd … the man hadn’t been paid yet. What a strange fellow!”
(a) Who is the speaker? Who is he speaking about?
Answer:
Naresh Dutt is speaking about Patol Babu.
(b) What was odd?
Answer:
The fact that Patol Babu had disappeared without waiting to be paid was odd.
(c) Why had he not waited?
Answer:
Patol Babu felt so satisfied with his performance that he did not feel the need to be paid.