NCERT Maths Solutions for Ex 3.5 class 10 Linear equations is the perfect guide to boost up your preparation during CBSE 10th Class Maths Examination.
RS Aggarwal Class 10 Solutions Chapter 3 Linear equations in two variables Ex 3E
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3E. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.
Question 1.
Solution:
Let cost of one chair = ₹ x
and cost of one table = ₹ y
According to the conditions,
5x + 4y = ₹ 5600 …(i)
4x + 3y = ₹ 4340 …(ii)
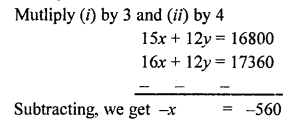
x = -560
and from (i)
5 x 560 + 4y = 5600
2800 + 4y = 5600
⇒ 4y = 5600 – 2800
⇒ 4y = 2800
⇒ y = 700
Cost of one chair = ₹ 560
and cost of one table = ₹ 700
Question 2.
Solution:
Let the cost of one spoon = ₹ x and cost of one fork = ₹ y
According to the conditions,
23x + 17y = 1770 …(i)
17x + 23y = 1830 …(ii)
Adding, we get
40x + 40y = 3600
Dividing by 40,
x + y = 90 …(iii)
and subtracting,
6x – 6y = -60
Dividing by 6,
x – y = -10 …(iv)
Adding (iii) and (iv)
2x = 80 ⇒ x = 40
and subtracting,
2y = 100 ⇒ y = 50
Cost of one spoon = ₹ 40
and cost of one fork = ₹ 50
Question 3.
Solution:
Let number of 25-paisa coins = x
and number 50-paisa coins = y
Total number of coins = 50
and total amount = ₹ 19.50 = 1950 paisa
x + y = 50 …(i)
25x + 50y = 1950
⇒ x + 2y = 78 …(ii)
Subtracting (i) from (ii), y = 28
x = 50 – y = 50 – 28 = 22
Number of 25-paisa coins = 22
and 50-paisa coins = 28
Question 4.
Solution:
Sum of two numbers = 137
and difference = 43
Let first number = x
and second number = y
x + y = 137 …..(i)
x – y = 43 ……(ii)
Adding, we get
2x = 180 ⇒ x = 90
and subtracting,
2y = 94
y = 47
First number = 90
and second number = 47
Question 5.
Solution:
Let first number = x
and second number = y
According to the conditions,
2x + 3y = 92 …(i)
4x – 7y = 2 …(ii)
Multiply (i) by 2 and (ii) by 1
4x + 6y = 184 …..(iii)
4x – 7y = 2 …….(iv)
Subtracting (iii) from (iv),
13y = 182
y = 14
From (i), 2x + 3y = 92
2x + 3 x 14 = 92
⇒ 2x + 42 = 92
⇒ 2x = 92 – 42 = 50
⇒ x = 25
First number = 25
Second number = 14
Question 6.
Solution:
Let first number = x
and second number = y
According to the conditions,
3x + y=142 …(i)
4x – y = 138 …(ii)
Adding, we get
7x = 280
⇒ x = 40
and from (i)
3 x 40 + y = 142
⇒ 120 + y = 142
⇒ y = 142 – 120 = 22
First number = 40,
second number = 22
Question 7.
Solution:
Let first greater number = x
and second smaller number = y
According to the conditions,
2x – 45 = y …(i)
2y – 21 = x …(ii)
Substituting the value of y in (ii),
2 (2x – 45) – 21 = x
⇒ 4x – 90 – 21 = x
⇒ 4x – x = 111
⇒ 3x = 111
⇒ x = 37
From (i),
y = 2 x 37 – 45 = 74 – 45 = 29
The numbers are 37, 29
Question 8.
Solution:
Let larger number = x
and smaller number = y
According to the conditions,
3x = 4 x y + 8 ⇒ 3x = 4y + 8 …….(i)
5y = x x 3 + 5 ⇒ 5y = 3x + 5 …(ii)
Substitute the value of 3x in (ii),
5y = 4y + 8 + 5
⇒ 5y – 4y = 13
⇒ y = 13
and 3x = 4 x 13 + 8 = 60
⇒ x = 20
Larger number = 20
and smaller number = 13
Question 9.
Solution:
Let first number = x and
second number = y
According to the conditions,
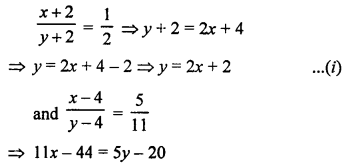
⇒ 11x – 44 = 5(2x + 2) – 20
⇒ 11x – 44 = 10x + 10 – 20
⇒ 11x – 10x = 10 – 20 + 44
⇒ x = 34
and y = 2 x 34 + 2 = 68 + 2 = 70
Numbers are 34 and 70
Question 10.
Solution:
Let first number = x
and second number (smaller) = y
According to the conditions,
x – y = 14
and x² – y² = 448
⇒ (x + y) (x – y) = 448
⇒ (x + y) x 14 = 448
⇒ x + y = 32 ……(i)
and x – y = 14 ……(ii)
Adding (i) and (ii),
2x = 46 ⇒ x = 23
and subtracting (i) and (ii),
2y = 18 ⇒ y = 9
Numbers are 23, 9
Question 11.
Solution:
Let ones digit of a two digit number = x
and tens digit = y
Number = x + 10y
By interchanging the digits,
Ones digit = y
and tens digit = x
Number = y + 10x
According to the conditions,
x + y = 12 ………. (i)
y + 10x = x + 10y + 18
⇒ y + 10x – x – 10y = 18
⇒ 9x – 9y = 18
⇒ x – y = 2 …(ii) (Dividing by 9)
Adding (i) and (ii),
2x = 14 ⇒ x = 7
and subtracting,
2y = 10 ⇒ y = 5
Number = 7 + 10 x 5 = 7 + 50 = 57
Question 12.
Solution:
Let one’s digit of a two digit number = x
and ten’s digit = y
Then number = x + 10y
After reversing the digits,
Ones digit = y
and ten’s digit = x
and number = y + 10x
According to the conditions,
x + 10y – 27 = y + 10x
⇒ y + 10x – x – 10y = -27
⇒ 9x – 9y = -27
⇒ x – y = -3 …(i)
and 7 (x + y) = x + 10y
7x + 7y = x+ 10y
⇒ 7x – x = 10y – 7y
⇒ 6x = 3y
⇒ 2x = y …(ii)
Substituting the value of y in (i)
x – 2x = -3
⇒ -x = -3
⇒ x = 3
y = 2x = 2 x 3 = 6
Number = x + 10y = 3 + 10 x 6 = 3 + 60 = 63
Question 13.
Solution:
Let one’s digit of a two digit number = x
and ten’s digit = y
Then number = x + 10y
After interchanging the digits,
One’s digit = y
and ten’s digit = x
Then number = y + 10x
According to the conditions,
y + 10x = x + 10y + 9
⇒ y + 10x – x – 10y = 9
⇒ 9x – 9y = 9
⇒ x – y = 1 …(i)
and x + y= 15 …(ii)
Adding, we get
2x = 16
x = 8
and subtracting,
2y = 14
⇒ y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78
Question 14.
Solution:
Let one’s digit of the two digit number = x
and ten’s digit = y
Then number = x + 10y
By reversing the digits,
One’s digit = y
and ten’s digit = x
Then number = y + 10x
Now, according to the conditions,
x + 10y + 18 = y + 10x
⇒ 18 = y + 10x – x – 10y
⇒ 9x – 9y = 18
⇒ x – y = 2 …(i)
and 4(x + y) + 3 = x + 10y
4x + 4y + 3 = x + 10y
⇒ 4x + 4y – x – 10y = -3
3x – 6y = -3
⇒ x – 2y = -1 ……..(ii)
Subtracting,
y = 3
and x = 2y – 1 = 2 x 3 – 1 = 6 – 1 = 5
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35
Question 15.
Solution:
Let ones digit of a two digit number = x
and tens digit = y
Then number = x + 10y
By reversing the digits,
One’s digit = y
and ten’s digit = x
and number = y + 10x
According to the conditions,
x + 10y – 9 = y + 10x
⇒ x + 10y – y – 10x = 9
⇒ -9x + 9y = 9
⇒x – y = -1 …(i) (Dividing by -9)
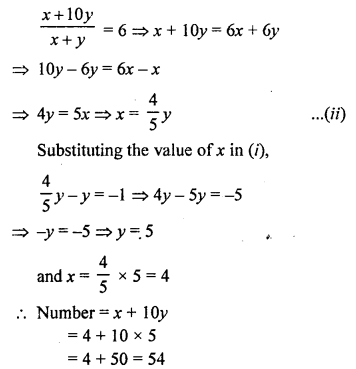
Question 16.
Solution:
Let the one’s digit of a two digit number = x
and ten’s digit = y
Then number = x + 10y
By interchanging the digits,
One’s digit = y
and ten’s digit = x
Then number = y + 10x
According to the conditions,
x + 10y + 18 = y + 10x
⇒ 18 = y + 10x – x – 10y
⇒ 9x – 9y = 18
⇒ x – y = 2 …(i)
and xy = 35 …(ii)
Now, (x + y)² = (x – y)² + 4xy = (2)² + 4 x 35 = 4 + 140 = 144 = (12)²
⇒ (x + y) = 12 …(iii)
Subtracting (i) from (iii), we get
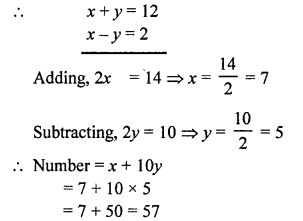
Question 17.
Solution:
Let one’s digit of a two digit number = x
and ten’s digit = y
Then number = x + 10y
After interchanging the digits One’s digit = y
Ten’s digit = x
Then number = y + 10x
According to the conditions,
x + 10y – 63 = y + 10x

Question 18.
Solution:
Let one’s digit of a two digit number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits,
One’s digit = y
and ten’s digit = x
Number = y + 10x
According to the conditions,
x + 10y + y + 10x = 121
⇒ 11x + 11y = 121
⇒ x + y = 11 …(i)
x – y = 3 …(ii)
Adding, we get
2x = 14 ⇒ x = 7
Subtracting,
2y = 8 ⇒ y = 4
Number = 7 + 10 x 4 = 7 + 40 = 47
or 4 + 10 x 7 = 4 + 70 = 74
Question 19.
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions,
x + y = 8 …(i)
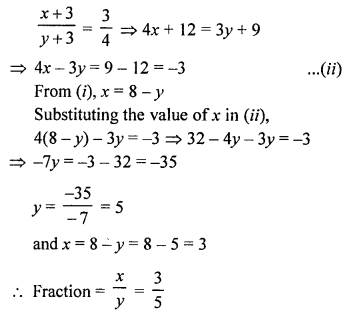
Question 20.
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions,
\(\frac { x + 2 }{ y }\) = \(\frac { 1 }{ 2 }\)
\(\frac { x }{ y – 1 }\) = \(\frac { 1 }{ 3 }\)
⇒ 2x + 4 = y …(i)
3x = y – 1 …(ii)
⇒ 3x = 2x + 4 – 1
⇒ 3x = 2x + 3
⇒ 3x – 2x = 3
⇒ x = 3
and y = 2x + 4 = 2 x 3 + 4 = 6 + 4 = 10
Fraction = \(\frac { 3 }{ 10 }\)
Question 21.
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions,
y – x = 11
y = 11 + x …(i)
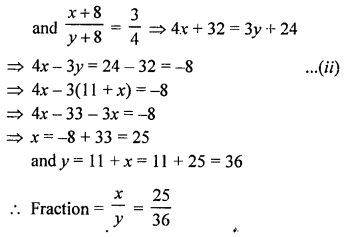
Question 22.
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions,
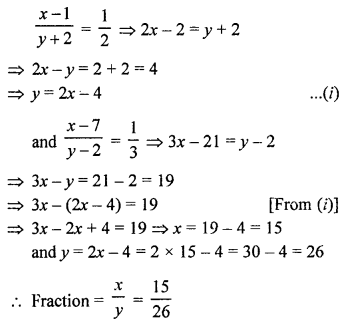
Question 23.
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction =
According to the conditions,
x + y = 4 + 2x
⇒ y = 4 + x …(i)
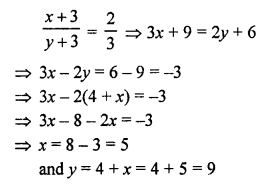
Fraction = \(\frac { x }{ y }\) = \(\frac { 5 }{ 9 }\)
Question 24.
Solution:
Let first number = x
and second number = y
According to the conditions,
x + y = 16
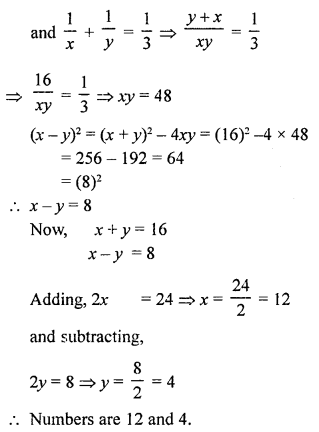
Question 25.
Solution:
Let in classroom A, the number of students = x
and in classroom B = y
According to the conditions,
x – 10 = y + 10
⇒ x – y = 10 + 10 = 20
⇒ x – y = 20 …(i)
and x + 20 = 2 (y – 20)
⇒ x + 20 = 2y – 40
⇒ x – 2y = -(40 + 20) = -60
x – 2y = -60 …(ii)
Subtracting, y = 80
and x – y = 20
⇒ x – 80 = 20
⇒ x = 20 + 80 = 100
Number of students in classroom A = 100 and in B = 80
Question 26.
Solution:
Let fixed charges = ₹ x
and other charges = ₹ y per km
According to the conditions,
For 80 km,
x + 80y = ₹ 1330 …(i)
and x + 90y = ₹ 1490 …(ii)
Subtracting (i) from (ii),
10y = 160 ⇒ y = 16
and from (i)
x + 80 x 16 = 1330
⇒ x + 1280 = 1330
⇒ x = 1330 – 1280 = 50
Fixed charges = ₹ 50
and rate per km = ₹ 16
Question 27.
Solution:
Let fixed charges of the hostel = ₹ x
and other charges per day = ₹ y
According to the conditions,
x + 25y = 4500 ……..(i)
x + 30y = 5200 ……(ii)
Subtracting (i) from (ii),
5y = 700
y = 140
and from (i),
x + 25 x 140 = 4500
⇒ x + 3500 = 4500
⇒ x = 4500 – 3500 = 1000
Fixed charges = ₹ 1000
and per day charges = ₹ 140
Question 28.
Solution:
Let first investment = ₹ x
and second investment = ₹ y
Rate of interest = 10% p.a. for first kind and 8% per second
Interest is for the first investment = ₹ 1350
and for the second = ₹ 1350 – ₹45 = ₹ 1305
According to the conditions,

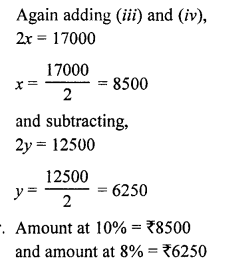
Question 29.
Solution:
Ratio in the income of A and B = 5 : 4
Let A’s income = ₹ 5x and
B’s income = ₹ 4x
and ratio in their expenditures = 7 : 5
Let A’s expenditure = 7y
and B’s expenditure = 5y
According to the conditions,
5x – 7y = 9000 …(i)
and 4x – 5y = 9000 …(ii)
Multiply (i) by 5 and (ii) by 7,
25x – 35y = 45000
28x – 37y = 63000
Subtracting, we get
3x = 18000
⇒ x = 6000
A’s income = 5x = 5 x 6000 = ₹ 30000
and B’s income = 4x = 4 x 6000 = ₹ 24000
Question 30.
Solution:
Let cost of one chair = ₹ x
and cost of one table = ₹ y
In first case,
Profit on chair = 25%
and on table = 10%
and selling price = ₹ 1520
According to the conditions,

Question 31.
Solution:
Distance between two stations A and B = 70 km
Let speed of first car (starting from A) = x km/hr
and speed of second car = y km/hr
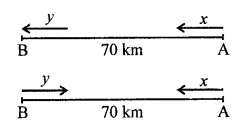
According to the conditions,
7x – 7y = 70
⇒ x – y = 10 …(i)
and x + y = 70 …(ii)
Adding (i) and (ii),
2x = 80 ⇒ x = 40
Subtracting (i) and (ii),
2y = 60 ⇒ y = 30
Speed of car A = 40 km/hr
and speed of car B = 30 km/hr
Question 32.
Solution:
Let uniform speed of the train = x km/hr
and time taken = y hours
Distance = x x y = xy km
Case I:
Speed = (x + 5) km/hr
and Time = (y – 3) hours
Distance = (x + 5) (y – 3)
(x + 5) (y – 3) = xy
⇒ xy – 3x + 5y – 15 = xy
-3x + 5y = 15 …(i)
Case II:
Speed = (x – 4) km/hr
and Time = (y + 3) hours
Distance = (x – 4) (y + 3)
(x – 4) (y + 3) = xy
⇒ xy + 3x – 4y – 12 = xy
3x – 4y = 12 …(ii)
Adding (i) and (ii),
y = 27
and from (i),
-3x + 5 x 27 = 15
⇒ -3x + 135 = 15
⇒ -3x = 15 – 135 = -120
⇒ x = 40
Speed of the train = 40 km/hr
and distance = 27 x 40 = 1080 km
Question 33.
Solution:
Let the speed of the train = x km/hr
and speed of taxi = y km/hr
According to the conditions,


Question 34.
Solution:
Distance between stations A and B = 160 km
Let the speed of the car starts from A = x km/hr
and speed of car starts from B = y km/hr
8x – 8y = 160
⇒ x – y = 20 …(i)
and 2x + 2y = 160
⇒ x + y = 80 …(ii)
Adding (i) and (ii)
2x = 100 ⇒ x = 50
and subtracting,
2y = 60 ⇒ y = 30
Speed of car starting from A = 50 km/hr
and from B = 30 km/hr
Question 35.
Solution:
Distance = 8 km
Let speed of sailor in still water = x km/hr
and speed of water = y km/hr
According to the conditions,
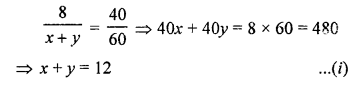

Question 36.
Solution:
Let speed of a boat = x km/hr
and speed of stream = y km/hr
According to the conditions,
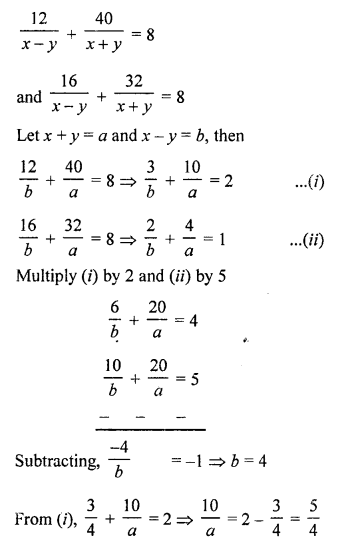
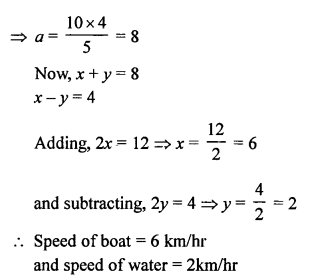
Question 37.
Solution:
Let a man can do a work in x days
His 1 day’s work = \(\frac { 1 }{ x }\)
and a boy can do a work in y days
His 1 day’s work = \(\frac { 1 }{ y }\)
According to the conditions,

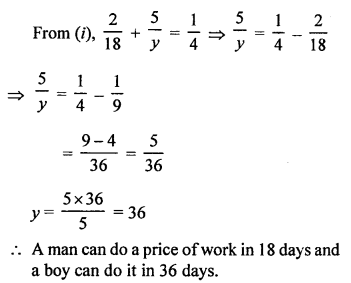
Question 38.
Solution:
Let length of a room = x m
and breadth = y m
and area = xy m²
According to the conditions,
x = y + 3 …(i)
(x + 3) (y – 2) = xy
xy – 2x + 3y – 6 = xy
-2x + 3y = 6 …(ii)
-2 (y + 3) + 3y = 6 [From (i)]
-2y – 6 + 3y = 6
⇒ y = 6 + 6 = 12
x = y + 3 = 12 + 3 = 15 …(ii)
Length of room = 15 m
and breadth = 12 m
Question 39.
Solution:
Let length of a rectangle = x m
and breadth = y m
Then area = x x y = xy m²
According to the conditions,
(x – 5) (y + 3) = xy – 8
⇒ xy + 3x – 5y – 15 = xy – 8
⇒ 3x – 5y = -8 + 15 = 7 …..(i)
and (x + 3) (y + 2) = xy + 74
⇒ xy + 2x + 3y + 6 = xy + 74
⇒ 2x + 3y = 74 – 6 = 68 …(ii)
Multiply (i) by 3 and (ii) by 5
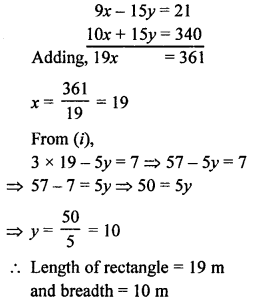
Question 40.
Solution:
Let length of a rectangle = x m
and breadth = y m
Then area = xy m²
According to the conditions,
(x + 3) (y – 4) = xy – 67
⇒ xy – 4x + 3y – 12 = xy – 67
⇒ -4x + 3y = -67 + 12 = -55
⇒ 4x – 3y = 55 …(i)
and (x – 1) (y + 4) = xy + 89
⇒ xy + 4x – y – 4 = xy + 89
⇒ 4x – y = 89 + 4 = 93 ….(ii)
⇒ y = 4x – 93
Substituting the value of y in (i),
4x – 3(4x – 93) = 55
⇒ 4x – 12x + 279 = 55
⇒ -8x = 55 – 279 = -224
⇒ x = 28
and y = 4x – 93 = 4 x 28 – 93 = 112 – 93 = 19
Length of rectangle = 28 m
and breadth = 19 m
Question 41.
Solution:
Let reservation charges = ₹ x
and cost of full ticket from Mumbai to Delhi
According to the conditions,
x + y = 4150 …(i)
2x + \(\frac { 3 }{ 2 }\) y = 6255
⇒ 4x + 3y = 12510 …(ii)
From (i), x = 4150 – y
Substituting the value of x in (ii),
4 (4150 – y) + 3y = 12510
⇒ 16600 – 4y + 3y = 12510
-y = 12510 – 16600
-y = -4090
⇒ y = 4090
and x = 4150 – y = 4150 – 4090 = 60
Reservation charges = ₹ 60
and cost of 1 ticket = ₹ 4090
Question 42.
Solution:
Let present age of a man = x years
and age of a son = y years
5 year’s hence,
Man’s age = x + 5 years
and son’s age = y + 5 years
x + 5 = 3 (y + 5) = 3y + 15
⇒ x – 3y = 15 – 5 = 10
x = 10 + 3y …(i)
and 5 years ago,
Man’s age = x – 5 years
and son’s age = y – 5 years
x – 5 = 7 (y – 5) = 7y – 35
x = 7y – 35 + 5 = 7y – 30 …(ii)
From (i) and (ii),
10 + 3y = 7y – 30
⇒ 7y – 3y = 10 + 30
⇒ 4y = 40
⇒ y = 10
and x = 10 + 3y = 10 + 3 x 10 = 10 + 30 = 40
Present age of a man = 40 years
and of son’s age = 10 years
Question 43.
Solution:
Let present age of a man = x years
and age of his son = y years
2 years ago,
Man’s age = x – 2 years
Son’s age = y – 2 years
x – 2 = 5 (y – 2)
⇒ x – 2 = 5y – 10
x = 5y – 10 + 2 = 5y – 8 …(i)
2 years later,
Man’s age = x + 2 years
and son’s age = y + 2 years
x + 2 = 3(y + 2) + 8
x + 2 = 3y + 6 + 8
⇒ x = 3y + 6 + 8 – 2 = 3y + 12 …(ii)
From (i) and (ii),
5y – 8 = 3y + 12
⇒ 5y – 3y = 12 + 8
⇒ 2y = 20
⇒ y = 10
and x = 5y – 8 = 5 x 10 – 8 = 50 – 8 = 42
Present age of man = 42 years
and age of son = 10 years
Question 44.
Solution:
Let age of father = x years
and age of his son = y years
According to the conditions,
2y + x = 10 …(i)
2x + y = 95 …(ii)
From (i),
x = 70 – 2y
Substituting the value of x in (ii),
2 (70 – 2y) + y = 95
⇒ 140 – 4y + y = 95
⇒ -3y = 95 – 140 = -45
⇒ -3y = -45
⇒ y = 15
and x = 70 – 2y = 70 – 2 x 15 = 70 – 30 = 40
Age of father = 40 years
and age of his son = 15 years
Question 45.
Solution:
Let present age of a woman = x years
and age of her daughter = y years
According to the conditions,
x = 3y + 3 …(i)
3 years hence,
Age of woman = x + 3 years
and age of her daughter = y + 3 years
x + 3 = 2 (y + 3) + 10
⇒ x + 3 = 2y + 6 + 10
⇒x = 2y + 16 – 3 = 2y + 13 …(ii)
From (i),
3y + 3 = 2y + 13
⇒ 3y – 2y = 13 – 3
⇒ y = 10
and x = 3y + 3 = 3 x 10 + 3 = 30 + 3 = 33
Present age of woman = 33 years
and age of her daughter = 10 years
Question 46.
Solution:
Let cost price of tea set = ₹ x
and of lemon set = ₹ y
According to the conditions,
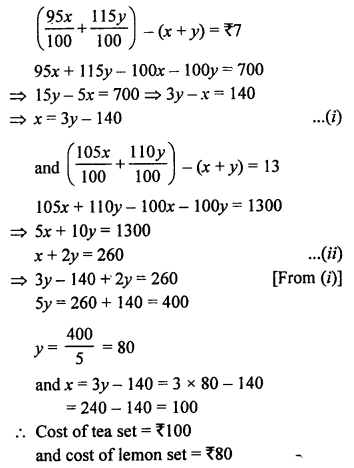
Question 47.
Solution:
Let fixed charges = ₹ x (for first three days)
and then additional charges for each day = ₹ y
According to the conditions,
Mona paid ₹ 27 for 7 dyas
x + (7 – 3) x y = 27
⇒ x + 4y = 27
and Tanvy paid ₹ 21 for 5 days
x + (5 – 3) y = 21
⇒ x + 2y = 21 …(ii)
Subtracting,
2y = 6 ⇒ y = 3
But x + 2y = 21
⇒ x + 2 x 3 = 21
⇒ x + 6 = 21
⇒ x = 21 – 6 = 15
Fixed charges = ₹ 15
and additional charges per day = ₹ 3
Question 48.
Solution:
Let x litres of 50% solution be mixed with y litres of 25% solution, then
x + y = 10 …(i)
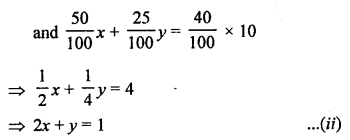
Subtracting (i) from (ii),
x = 6
and x + y = 10
⇒ 6 + y = 10
⇒ y = 10 – 6 = 4
50% solution = 6 litres
and 25% solution = 4 litres
Question 49.
Solution:
Let x g of 18 carat be mixed with y g of 12 carat gold to get 120 g of 16 carat gold, then
x + y = 120 …(i)
Now, gold % in 18-carat gold = \(\frac { 18 }{ 24 }\) x 100 = 75%

⇒ 3x + 2y = 320 …(ii)
From (i),
x = 120 – y
Substituting the value of x in (ii),
3 (120 – y) + 2y = 320
⇒ 360 – 3y + 2y = 320
⇒ -y = 320 – 360
⇒ -y = -40
⇒ y = 40
and 40 + x = 120
⇒ x = 120 – 40 = 80
Hence, 18 carat gold = 80 g
and 12-carat gold = 40 g
Question 50.
Solution:
Let x litres of 90% pure solution be mixed withy litres of 97% pure solution to get 21 litres of 95% pure solution. Then,
x + y = 21 …(i)
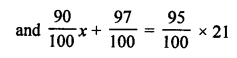
⇒ 90x + 97y = 1995
From (i), x = 21 – y
Substituting the value of x in (ii),
90 (21 – y) + 97y = 1995
⇒ 1890 – 90y + 97y = 1995
⇒ 7y = 1995 – 1890 = 105
⇒ y =15
and x = 21 – y = 21 – 15 = 6
90% pure solution = 6 litres
and 97% pure solution = 15 litres
Question 51.
Solution:
Let larger supplementary angle = x°
and smaller angle = y°
According to the conditions,
x + y = 180° …(i)
x = y + 18° …(ii)
From (i),
y + 18° + y = 180°
⇒ 2y = 180° – 18° = 162°
⇒ 2y = 162°
⇒ y = 81°
and x= 180°- 81° = 99°
Hence, angles are 99° and 81°
Question 52.
Solution:
In ∆ABC,
∠A = x, ∠B = (3x – 2)°, ∠C = y°, ∠C – ∠B = 9°

Question 53.
Solution:
In a cyclic quadrilateral ABCD,

Hope given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3E are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.