NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles Ex 10.3 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles Ex 10.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 10 |
| Chapter Name | Areas of Parallelograms and Triangles |
| Exercise | Ex 10.3 |
| Number of Questions Solved | 16 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles Ex 10.3
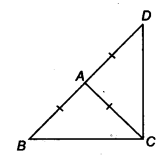
Question 1.
In figure, E is any point on median AD of a ∆ABC. Show that ar (ABE) = ar (ACE).
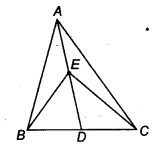
Solution:
Given: AD is a median of AABC and E is a any point on AD.
∵ AD is the median of ∆ABC.
ar (∆ABD) = ar (∆ACD) … (i)
[∵ A median of a triangle divide it into two triangles of equal areas]
Also, ED is the median of ∆EBC.
ar (∆BED) = ar (∆CED) …(ii)
On subtracting Eq. (ii) from Eq. (i), we get
ar (∆ABD) – ar (∆BED) = ar (∆ACD) – ar (∆CED)
⇒ ar (∆ABE) = ar (∆ACE)
Hence proved.
Question 2.
In a triangle ABC, E is the mid-point of median AD. Show that ax (BED) = \(\frac { 1 }{ 4 }\) ar (ABC).
Solution:
Given: ABC is a triangle, E is the mid-point of the median AD.
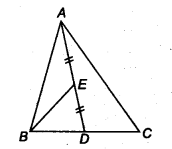
We know that, median divides a triangle into two triangles of equal areas.
∴ ar (∆ABD) = ar (∆ADC)
ar (∆ABD) = \(\frac { 1 }{ 2 }\) ar (∆ABC) ……(i)
In ∆ABD, BE is the median.
∴ ar (∆BED) = ar (∆BAE)
or ar (∆BED) = \(\frac { 1 }{ 2 }\) ar (∆ABD)
⇒ ar (∆ BED) = 1 x -1 ar (∆ABC) [Put the value from Eq. (i)]
⇒ ar (∆BED) = \(\frac { 1 }{ 4 }\) ar (∆ABC)
Hence proved.
Question 3.
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
Given: a parallelogram ABCD. Its diagonals AC and BD intersect at O.
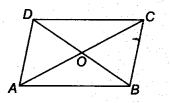
We have to prove that, diagonals AC and BD divides parallelogram into four triangle of equal area i.e.,
ar (∆ OAB) = ar (∆ OBC) = ar (∆ OCD) = ar (∆ OAD)
we know that, the diagonals of a parallelogram bisect each other, so we have OA = OC and OB = OD.
Also, a median of a triangle divides it into two triangles of equal areas.
So, in ∆ABC, BO is the median.
∴ ar (∆OAB) = ar (∆OBC) ,..(i)
Also, in ∆ABD, AO is the median.
∴ ar (∆OAB) = ar (∆OAD) .. ,(ii)
Similarly in AACD, DO is the median.
∴ ar (∆OAD) = ar (∆OCD) .. .(iii)
From Eqs. (i), (ii) and (iii), we get
∴ ar (∆OAB) = ar (∆OBC) = ar (∆OCD) = ar(∆OAD)
Question 4.
In figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that
ar(ABC) = ar(ABD)
Solution:
Given: ABC and ABD are two triangles on the same base AB.
The line segment CD is bisected by AE = O. ∵ OC = OD
In ∆ACD, we have
OC = OD (Given)
∴ AO is the median.
Since, the median divides a triangle in two triangles of equal areas.
∴ ar (∆AOQ = ar (∆AOD) ….(i)
Similarly, in ∆BCD, ar (BOC) = ar (BOD) …(ii)
On adding Eqs. (i) and (ii), we get
ar (∆ AOC) + ar (∆ BOC) = ar (∆ AOD) + ar (∆ BOD)
⇒ ar (∆ABC) = ar (ABD)
Question 5.
D,E and F are respectively the mid-points of the sides BC, CA and AB of a ∆ABC. Show that
(i) BDEF is a parallelogram.
(ii) ar(∆DEF) = \(\frac { 1 }{ 4 }\) ar (∆ABC)
(iii) ar(||gm BDEF) = \(\frac { 1 }{ 2 }\) ar(∆ ABC)
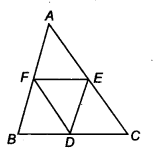
Solution:
Given: ABC is a triangle in which the mid-points of sides AB, CA and BC are, respectively F, E, D.
(i) Since, E and F are the mid-points of AC and AB.
∴ BC || EF and EF = \(\frac { 1 }{ 2 }\) BC = BD (By mid-point theorem)
Similarly, DE || AB and DE = \(\frac { 1 }{ 2 }\) AB = BF
Hence, BDEF is a parallelogram.
(ii) Similarly, we can prove that both FDCE and AFDE are also parallelogram. Now, BDEF is a parallelogram and its diagonal FD divides the parallelogram in two triangles of equal areas.
∴ ar (∆ BDF) = ar (∆ DEF) …(i)
Similarly, in parallelogram ar (∆ EDO) = ar (∆ DEF)
and In parallelogram …(ii)
AFDE, ar (∆ AFE) = ar (∆ DEF) .. .(iii)
From Eqs. (i), (ii) and (iii), we get
ar (∆ AFE) = ar (∆ DEF)
= ar (∆ BDF) = ar (∆ EDC) … (iv)
∵ ar (∆ AFE) + ar (∆ DEF) + ar (∆ EDC) + ar (∆ BDF) = ar (∆ ABC)
∴ 4 [ar (∆ DEF)] = ar (∆ ABC) [From Eq. (iv)]
⇒ ar (∆ DEF) = \(\frac { 1 }{ 4 }\) ar (∆ ABC) …(v)
(iii) ar (|| gm BDEF) = ar (∆ DEF) + ar (∆ FBD)
= 2ar (∆ DEF) [From Eq. (iv)]
= 2 . \(\frac { 1 }{ 4 }\) ar (∆ ABC) [FromEq. (v)]
= \(\frac { 1 }{ 2 }\) ar (A ABC)
Question 6.
In figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that
(i) ar(DOC) = ar(AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram
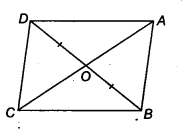
Solution:
Given: ABCD is a .quadrilateral and its diagonals AC and BD intersect at O such that OB = OD. Now,
draw DP ⊥ AC and BR ⊥ AC
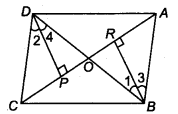
In ∆ DOP and ∆ BOR, we have
∠ DPO = ∠ BRO (Each = 90°)
∠ DOP = ∠BOR (Vertically opposite angles)
and OD = OB (Given)
∴ By AASrule, we get
∆ DOP ≅ ∆ BOR (Each = 90°)
So, ar (∆ DOP) = ar (∆ BOR) ….(i)
Again, in ∆ DCP and ∆ BAR,
∠ DPC = ∠ BRA (Each = 90°)
DC= AB (Given)
and DP = BR ( ∵ ∆ BOR ≅ ∆ DON ⇒ BR = DN)
∴ By SAS rule, we get
∆ DCP = ∆ BAR ….(ii)
∴ ar (∆DCP) = ar (∆ BAR)
On adding Eqs. (i) and (ii), we get
ar (DOP) + ar (DCP) = ar (BOR) + ar (BAP)
Hence, ar (DOC) = ar (AOB)
(ii) ar (DOC) = ar (AOB)
∴ ar (DOC) + ar (BOC) = ar (AOB) + ar (BOC) [Add ar (BOC) on both sides]
⇒ ar (DCB) = ar (ACB)
(iii) Since, ∆ DCS and ∆ACB have equal areas and have the same base. So, ∆ DCB and ∆ ACB must lie between the same parallels.
∴ DA || CB ,
FromEq.(i), ∠1 = ∠4 …(iii)
FromEq. (ii), ∠ 3 = ∠2 …(iv)
On adding Eqs. (iii) and (iv), we get
∠1+∠3 = ∠2 + ∠4
So, ∠ CDB = ∠ ABD
∴ CD|| AB
Hence, ABCD is a parallelogram.
Question 7.
D and E are points on sides AB and AC respectively of ∆ ABC such that ar (DBC) = ar (EBC). Prove that DE || BC.
Solution:
Given, a ∆ ABC and D and E are points on sides AB and AC respectively, also ar (DBQ = ar (ESC)
Therefore, ∆DBC and ∆EBC are equal in area and have a same base BC.
So, altitude from D of ∆DBC = altitude from E of ∆EBC
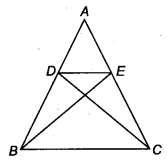
Hence, ∆ DBC and ∆ EBC are between the same parallels.
i.e., DE || BC.
Question 8.
XY is a line parallel to side BC of a ∆ ABC. If BE ||AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) =ar (ACF)
Solution:
Given: a ∆ ABC in which XY || BC also BE || AC is BE || CY and CF || AB i.e., CF || XB.
Now, since XY || SC and CY || BE
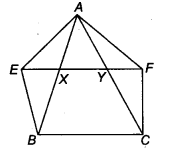
∴ EYCB is a parallelogram.
Since ∆ ABE and parallelogram EYCB lie on the same base BE and between the same parallel lines BE and AC.
So, ar (∆ ABE) = \(\frac { 1 }{ 2 }\) ar (EYCB) .. .(i)
Again, CF || AB and XF || BC
∴ BCFX is a parallelogram.
Since, ∆ ACF and parallelogram BCFX lie on the same base CF and between the same parallel lines AB and FC.
∴ ar (∆ ACF) = \(\frac { 1 }{ 2 }\) ar (BCFX) …(ii)
Now, parallelogram BCFX and parallelogram BCYE are on the same base BC and between the same parallels BC and EF.
∴ ar (BCFX) = ar (BCYE) …(iii)
From Eqs. (i), (ii) aad (iii), we get
ar (∆ ABE) = ar (∆ ACF)
Question 9.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then A parallelogram PBQR is completed (see figure).
Show that ax (ABCD) = ar(PBQR).
[Hint Join AC and PQ. Now compare ar (ACQ) and ar (APQ).]
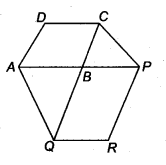
Solution:
Given: two parallelogram ABCD and PBQR.
Join AC and PQ, since PQ and AC and are diagonals of || gm PBQR and || gm ABCD respectively, therefore
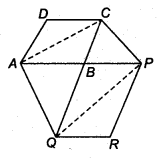
ar (∆ ABC) = \(\frac { 1 }{ 2 }\) ar (ABCD) …(i)
[∵ Diagonal of a parallelogram divide it into two triangles of equal area.]
and ar (ABQ) = \(\frac { 1 }{ 2 }\) ar (PBQR) .. .(ii)
Now, ∆ACQ and ∆AQP are on the same base AQ and between the same parallels AQ and CP.
∴ ar (ACQ) = ar (AQP)
⇒ ar (ACQ) – ar (ABQ) = ar (AQP) – ar (ABQ) [Subtract ar (ABQ) on both sides]
⇒ ar (∆ ABQ = ar (∆ BPQ)
⇒ \(\frac { 1 }{ 2 }\) ar (ABCD) = \(\frac { 1 }{ 2 }\) ar (PBQR) [From. Eqs. (i) and (ii)]
⇒ ar (ABCD) = ar (PBQR)
Question 10.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC)
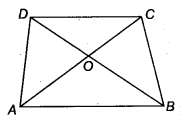
Solution:
Given: diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O.
Now, ∆ ABC and ∆ ABD being on the same base AB and between the same parallels AB and DC.
ar (∆ ABD) = ar (∆ABC)
On subtracting ar (∆AOB) from both sides, we get
ar (∆ ABD) – ar (∆AOB) = ar (∆ABC) – ar (∆AOB)
⇒ ar (∆AOD) = ar (∆BOC)
Question 11.
In figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
Solution:
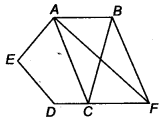
Given, ABCDE is a pentagon and BF || AC.
(i) ∆ACB and ∆ACF being on the same base AC and between the same parallels AC and BF.
∴ ar (∆ ACB) = ar (∆ ACF) …(i)
(ii) ar (AEDF) = ar (AEDQ + ar (∆ACF)
= ar (AEDC) + ar (∆ ACB) [From Eq. (i)]
= ar (ABCDE)
Question 12.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:
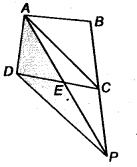
Let ABCD be the plot of land of the shape of a quadrilateral. Let the portion ADE be taken over by the Gram Panchayat of the village from one corner D to construct a Health Centre.
Join, AC draw a line through D parallel to AC to meet BC produced in P. Then, Itwaari must be given the land ECP adjoining his plot so as to from a triangular plot ABP as then.
ar (∆ ADE) = ar (∆ PEC)
Now, ∆ DAP and ∆ DCP are on the same base DP and between the same parallel DP and AC.
∴ ar (∆ DAP) = ar (∆DCP)
⇒ ar (∆ DAP) – ar (∆ DEP) = ar (∆ DCP) – ar (∆ DEP) (Subtracting the same area from both sides)
⇒ ar (∆ ADE) = ar (∆ PCE)
⇒ ar (∆ DAE) + ar (ABCD) = ar (∆PCE) + ar (ABCE) (Adding the same area on both sides)
⇒ ar (ABCD) = ar (∆ABP)
Question 13.
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX) = ar(ACY). [Hint Join IX]
Solution:
Given: ABCD is a trapezium and AB || CD. Also, XY || AC.
Now, join CX. Since, ∆ ADX and ∆ACX lie on the same base AX and between the same parallel lines AB and DC.
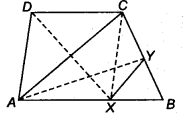
∴ ar(∆ ADX) = ar(∆ ACX) …(i)
Again, ∆ ACX and ∆ ACY lie on the same base AC and between the same parallel lines AC and XY.
∴ ar(∆ ACX) = ar(∆ ACY) …(ii)
Hence, from Eqs. (i) and (ii), we get
ar(∆ ADX) = ar(∆ ACY)
Question 14.
In figure, AP || BQ || CR. Prove that ar(AQC) = ax(PBR).
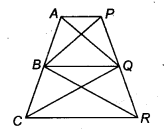
Solution:
According to given figure, we get
ar (∆PBR) = ar (∆PBQ) + ar (∆QBR) …..(i)
and ar(∆ AQC) = ar (∆ AQB)+ ar (∆ BQC) …(ii)
Since, ar(∆ BQC) = ar (∆ QBR) …(iii)
[Since, ∆BQC and ∆QBR lie on the same base BQ and between the same parallel lines BQ and CR]
Similarly, ar (AQB) = ar (PBQ) …..(iv)
On adding Eq. (iii) and (iv), we get
ar (∆BQC + ar(∆AQB) = ar (∆QBR) + ar (∆PBQ).
On putting the values from Eqs. (i) and (ii), we get
ar(∆ AQC) = ar(∆ PBR)
Question 15.
Diagonals AC and BD of a quadrilateral ABCD intersect at 0 in such a way that ax(AOD) = ar(BOC). Prove that ABCD is a trapezium.
Solution:
Given: ABCD is a quadrilateral and diagonal AC and BD intersect at O. Also,
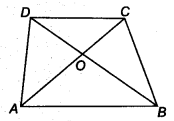
ar(∆ AOD) = ar(∆ BOC)
On adding both sides ar (∆ AOB), we get
ar(∆ AOD) + ar(∆ AOB) = ar(∆ BOC) + ar(∆ AOB)
⇒ ar(∆ ADB) = ar(∆ ACB)
Now, ∆ ACB and ∆ ADB lie on same base AB
and ar(∆ ADB) = ar(∆ ACB)
Hence, ∆ ACB and ∆ ADB lie between same parallel lines.
∴ AB || DC
Hence, ABCD is a trapezium.
Question 16.
In figure ax(DRC) = ar(DPC) and ai(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
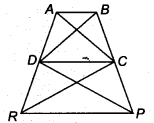
Solution:
Given,
ar (∆ DPC) = ar(∆ DRC) ……(i)
and ar(∆ BDP) = ar(∆ ARC) ……(ii)
On subtracting Eq. (i) from Eq. (ii), we get
ar(∆ BDP) – ar(∆ DPC) = ar(∆ ARC) – ar(∆ DRC)
⇒ ar(∆ BDC) = ar(∆ ADC)
Since, these two triangles are on the same base DC.
∴ DC || AB
Hence, ABCD is a trapezium.
Also, ar(∆ DRQ = ar(∆ DPQ
Since both triangles have the same base DC.
∴ RP || DC
Hence, PRCD is a trapezium.
We hope the NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles Ex 10.3 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles Ex 10.3, drop a comment below and we will get back to you at the earliest.