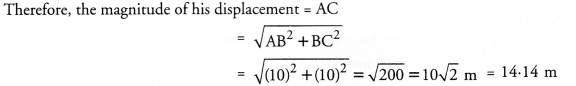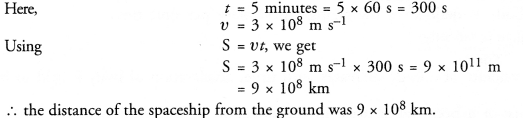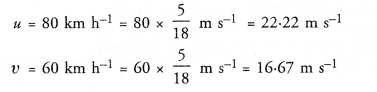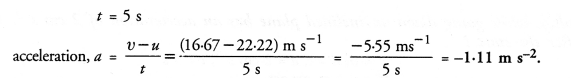RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.1
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
Mark the correct alternative in each of the following:
Question 1.
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) 3 : 1
Solution:
Two parallelograms which are on the same base and between the same parallels are equal in area
∴ Ratio in their areas =1 : 1 (c)
Question 2.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 1 : 3
Solution:
A triangle and a parallelogram which are on the same base and between the same parallels, then area of triangle is half the area of the parallelogram
∴ Their ratio =1:2 (c)
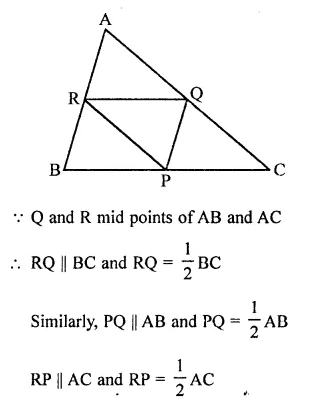
Question 3.
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of sides of ∆ABC. Then the area of ∆PQR is
(a) 12 sq. units
(b) 6 sq. units
(c) 4 sq. units
(d) 3 sq. units
Solution:
Area of ∆ABC = 24 sq. units
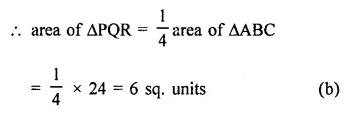
Question 4.
The median of a triangle divides it into two
(a) congruent triangle
(b) isosceles triangles
(c) right triangles
(d) triangles of equal areas
Solution:
The median of a triangle divides it into two triangles equal in area (d)
Question 5.
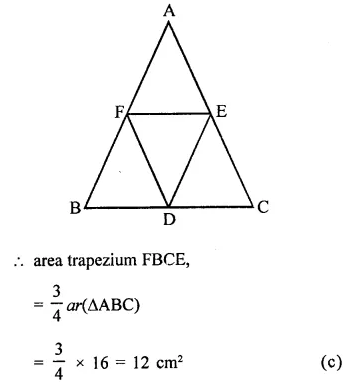
In a ∆ABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If
ar(∆ABC) = 16 cm2, then ar(trapezium FBCE) =
(a) 4 cm²
(b) 8 cm²
(c) 12 cm²
(d) 10 cm²
Solution:
In ∆ABC, D, E and F are the mid points of sides BC, CA and AB respectively
ar(∆ABC) = 16 cm²
Question 6.
ABCD is a parallelogram. P is any point on CD. If ar(∆DPA) = 15 cm² and ar(∆APC) = 20 cm², then ar(∆APB) =
(a) 15 cm²
(b) 20 cm²
(c) 35 cm²
(d) 30 cm²
Solution:
In ||gm ABCD, P is any point on CD
AP, AC and PB are joined
ar(∆DPA) =15 cm²
ar(∆APC) = 20 cm²
Adding, ar(∆ADC) = 15 + 20 = 35 cm²
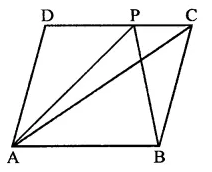
∵ AC divides it into two triangles equal in area
∴ ar(∆ACB) = ar(∆ADC) = 35 cm²
∵ ∆APB and ∆ACB are on the same base
AB and between the same parallels
∴ ar(∆APB) = ar(∆ACB) = 35 cm²(c)
Question 7.
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
(a) 28 cm²
(b) 48 cm²
(c) 96 cm²
(d) 24 cm²
Solution:
In rhombus ABCD,
P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively and are joined in order to get a quad. PQRS
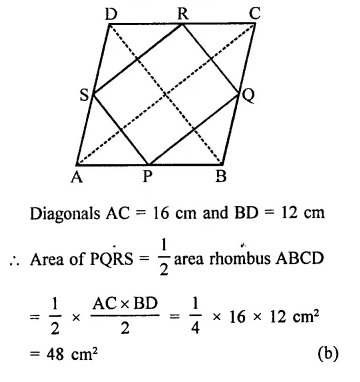
Question 8.
A, B, C, D are mid points of sides of parallelogram PQRS. If ar(PQRS) = 36 cm²,then ar(ABCD) =
(a) 24 cm²
(b) 18 cm²
(c) 30 cm²
(d) 36 cm²
Solution:
A, B, C and D are the mid points of a ||gm PQRS
Area of PQRS = 36 cm²
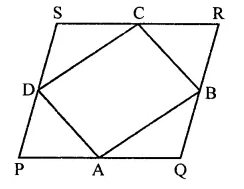
The area of ||gm formed by joining AB, BC, CD and DA

Question 9.
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is
(a) a rhombus of area 24 cm²
(b) a rectangle of area 24 cm²
(c) a square of area 26 cm²
(d) a trapezium of area 14 cm²
Solution:
Let P, Q, R, S be the mid points of sides of a rectangle ABCD. Whose sides 8 cm and 6 cm
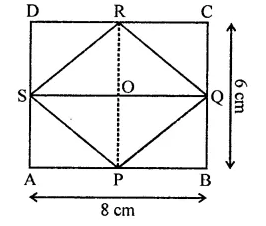
Their PQRS is a rhombus
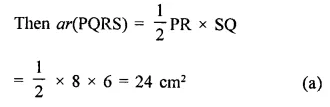
Question 10.
If AD is median of ∆ABC and P is a point on AC such that ar(∆ADP) : ar(∆ABD) = 2:3, then ar(∆PDC) : ar(∆ABC) is
(a) 1 : 5
(b) 1 : 5
(c) 1 : 6
(d) 3 : 5
Solution:
AD is the median of ∆ABC,
P is a point on AC such that
ar(∆ADP) : ar(∆ABD) = 2:3
Let area of ∆ADP = 2×2
Then area of ∆ABD = 3×2
But area of AABD = \(\frac { 1 }{ 2 }\) area AABC
∴ Area ∆ABC = 2 x area of ∆ABD
= 2 x 3x² = 6x²
and area of ∆PDC = area ∆ADC – (ar∆ADP) = area ∆ABD – ar ∆ADP
= 3x² – 2x² = x²
∴ Ratio = x² : 6x²
= 1 : 6 (c)
Question 11.
Medians of AABC, intersect at G. If ar(∆ABC) = 27 cm2, then ar(∆BGC) =
(a) 6 cm2
(b) 9 cm2
(c) 12 cm2
(d) 18 cm2
Solution:
In ∆ABC, AD, BE and CF are the medians which intersect each other at G
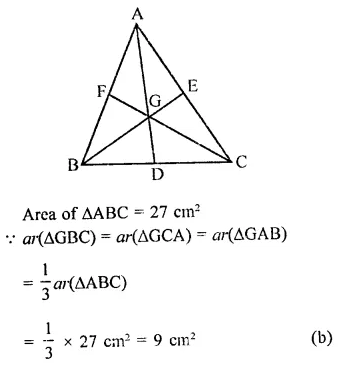
Question 12.
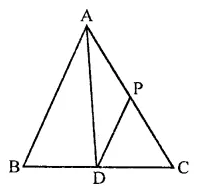
In a ∆ABC if D and E are mid-points of BC and AD respectively such that ar(∆AEC) = 4 cm², then ar(∆BEC) =
(a) 4 cm²
(b) 6 cm²
(c) 8 cm²
(d) 12 cm²
Solution:
In ∆ABC, D and E are the mid points of BC and AD
Join BE and CE ar(∆AEC) = 4 cm²
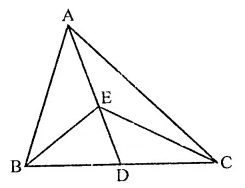
In ∆ABC,
∵ AD is the median of BC
∴ ar(∆ABD) = ar(∆ACD)
Similarly in ∆EBC,
ED is the median
∴ ar(∆EBD) = ar(∆ECD)
and in ∆ADC, CE is the median
∴ ar(∆FDC) = ar(∆AEC)
= 4 cm
∴ar∆EBC = 2 x ar(∆EDC)
= 2 x 4 = 8 cm (c)
Question 13.
In the figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =
(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
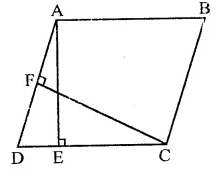
Solution:
In ||gm ABCD, AB = 12 cm AE = 7.5 cm
∴ Area of ||gm ABCD = base x height = AB x AE = 12 x 7.5 cm² = 90 cm²
Now area ||gm ABCD = 90 cm²
and altitude CF = 15 cm
∴ Base AD = \(\frac { Area }{ Altitude }\) = \(\frac { 90 }{ 15 }\) = 6 cm (b)
Question 14.
In the figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SR respectively and diagonal SQ is joined. The ratio ar(||gm XQRY) : ar(∆QSR) =
(a) 1 : 4
(b) 2 : 1
(c) 1 : 2
(d) 1 : 1
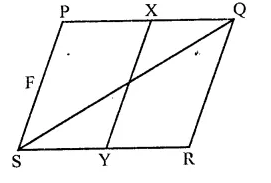
Solution:
In ||gm PQRS, X and Y are the mid points of PQ and SR respectively XY and SQ are joined.
∵ XY bisects PQ and SR
∴ PXYS and XQRY are also ||gms and ar(∆PXYS) = nr(∆XQRY)
∵ ||gm PQRS and AQSR are on the same base and between the same parallel lines
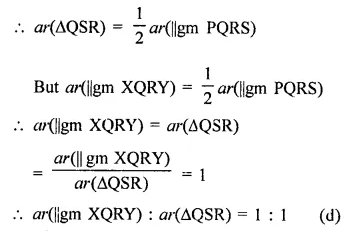
Question 15.
Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ∆AOD is
(a) ∆AOB
(b) ∆BOC
(c) ∆DOC
(d) ∆ADC
Solution:
In trapezium ABCD, diagonals AC and BD intersect each other at O. AB || DC
∆ABC and ∆ABD are on the same base and between the same parallels
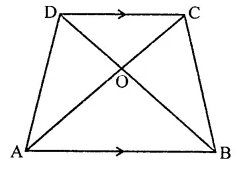
∴ ar(∆ABC) = or(∆ABD)
Subtracting ar(∆AOB)
ar(∆ABC) – ar(∆AOB) = ar(∆ADB) – ar(∆AOB)
⇒ ar(∆BOC) = ar(∆AOD)
ar(∆AOD) = ar(∆BOC) (c)
Question 16.
ABCD is a trapezium in which AB || DC. If ar(∆ABD) = 24 cm² and AB = 8 cm, then height of ∆ABC is
(a) 3 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Solution:
In trapezium ABCD, AB || DC
AC and BD are joined
ar(∆ABD) = 24 cm2
AB = 8 cm,
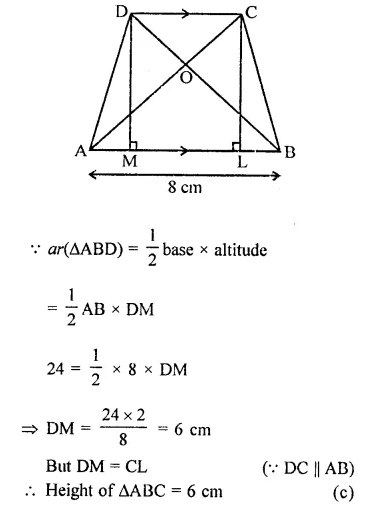
Question 17.
ABCD is a trapezium with parallel sides AB = a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFE and EFCD is
(a) a : b
(b) (a + 3b) : (3a + b)
(c) (3a + b) : (a + 3b)
(d) (2a + b) : (3a + b)
Solution:
In quadrilateral ABCD, E and F are the mid points of AD and BC
AB = a, CD = b
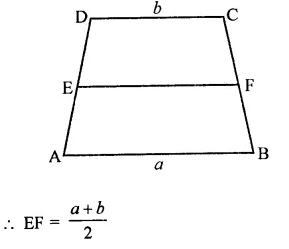
Let h be the height of trapezium ABCD then height of each quadrilateral
ABFE = altitude of quadrilateral EFCD = \(\frac { h }{ 2 }\)
Now area of trap. ABFE = \(\frac { 1 }{ 2 }\) (sum of parallel sides) x altitude
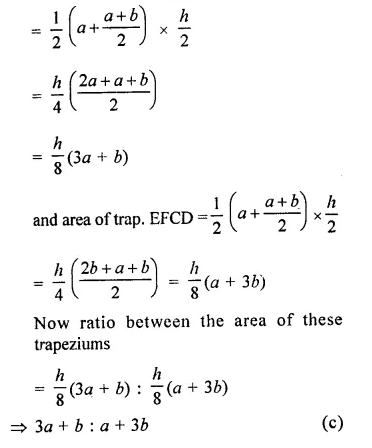
Question 18.
ABCD is a rectangle with O as any point in its interior. If or(∆AOD) = 3 cm2 and ar(∆BOC) = 6 cm2, then area of rectangle ABCD is
(a) 9 cm2
(b) 12 cm2
(c) 15 cm2
(d) 18 cm2
Solution:
In rectangle ABCD, O is any point
ar(∆AOD) = 3 cm2
and ar(∆BOC) = 6 cm2
Join OA, OB, OC and OD
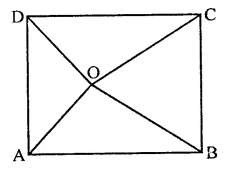
We know that if O is any point in ABCD Then ar(AOB) + ar(COD) = ar(AOB) + ar(BOC)
= 3 + 6 = 9 cm
∴ ar(rect. ABCD) = 2 x 9 = 18 cm (d)
Question 19.
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to
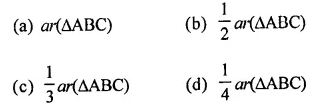
Solution:
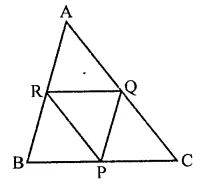
P,Q and R the mid points of the sides of a ∆ABC then area of any parallelogram formed by the mid points and one vertex of the given triangle has area = \(\frac { 1 }{ 2 }\) area ∆ABC (b)
Question 20.
In the figure, ABCD and FECG are parallelograms equal in area. If ar(∆AQE) = 12 cm2, then ar(||gm FGBQ) =
(a) 12 cm2
(b) 20 cm2
(c) 24 cm2
(d) 36 cm2
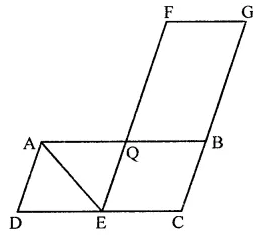
Solution:
In the figure, ABCD and EFCG are parallelograms equal in area and ar(∆AQE) = 12 cm2
In ||gm AQED, AE is the diagonal
∴ ar(∆AQE) = \(\frac { 1 }{ 2 }\) ar(||gm AQED)
⇒ 12 cm2 = \(\frac { 1 }{ 2 }\) ar(||gm AQED)
∴ ar(||gm AQED) = 24 cm2
∵ ar ||gm ABCD = ar ||gm FECG
⇒ ar(||gm ∆QED) + ar(|| gm QBCE)
= ar(||gm QBCE) + ar(||gm FGBQ)
⇒ ar(||gm ∆QED) = ar(||gm FGBQ)
= 24 cm2 (c)
Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.