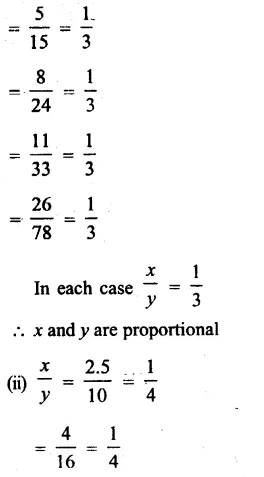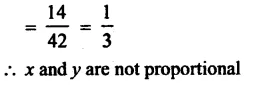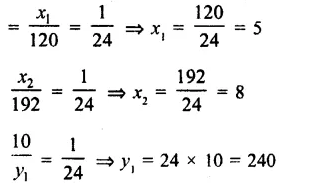Prasanna

NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion

by

NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion

MULTIPLE CHOICE QUESTIONS

Question 1.
Which of the following statement is not correct for an object moving along a straight path in an accelerated motion ?
(a) Its speed keeps changing
(b) Its velocity always changes
(c) It always goes away from the earth
(d) A force is always acting on it.
Answer:
(c).

More Resources

Question 2.
According to the third law of motion, action and reaction
(a) always act on the same body
(b) always act on different bodies in opposite directions
(c) have same magnitude and directions
(d) act on either body at normal to each other.
Answer:
(b).

Question 3.
A goalkeeper in a game of football pulls his hands backwards after holding the ball shot at the goal. This enables the goal keeper to
(a) exert larger force on the ball
(b) reduce the force exerted by the ball on hands
(c) increase the rate of change of momentum
(d) decrease the rate of change of momentum.
Answer:
(b) Explanation :
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 1

Question 4.
By pulling his hands backwards, he increases the time to reduce the momentum of the ball. Hence, less force is exerted on his hands. The inertia of an object tends to cause the object
(a) to increase its speed
(b) to decrease its speed
(c) to resist any change in its state of motion
(d) to decelerate due to friction.
Answer:
(c).

Question 5.
A passenger in a moving train tosses a coin which falls behind him, it means that motion of the train is
(a) accelerated
(b) uniform
(c) retarded
(d) along circular tracks.
Answer:
(a).

Question 6.
An object of mass 2 kg is sliding with a constant velocity of 4 m s-1 on a frictionless horizontal table. The force required to keep the object moving with the same velocity is
(a) 32 N
(b) 0 N
(c) 2 N
(d) 8 N.
Answer:
(b) Explanation : No force is needed to keep the object moving with constant velocity.

Question 7.
Rocket works on the principle of conservation of
(a) mass
(b) energy
(c) momentum
(d) velocity.
Answer:
(c).

Question 8.
A water tanker filled up to 2/3 of its height is moving with a uniform speed. On sudden application of the brake, the water in the tank would
(a) move backward
(b) move forward
(c) be unaffected
(d) rise upwards.
Answer:
(b) Explanation : It is due to inertia of motion.

SHORT ANSWER QUESTIONS

Question 9.
There are three solids made up of aluminium, steel and wood, of the same shape and same volume. Which of them would have highest inertia? (CBSE 2012)
Answer:
Density of steel is more than that of aluminium and wood, so its mass is greater than the solids made of aluminium and wood. Inertia depends on the mass of object. Hence, steel has the highest inertia.

Question 10.
Two balls of the same size but of different materials, rubber and iron are kept on the smooth surface of a moving trains. The brakes are applied suddenly to stop the train. Will the balls start rolling ? If so, in which direction ? Will they move with the same speed ? Justify your answer. (CBSE Sample Paper)
Answer:
When train slows down, balls remain in motion due to inertia of motion. Hence, balls start rolling in the forward direction. Since mass of both the balls are different, so they move with different speed.

Question 11.
Two identical bullets are fired one by a light rifle and another by a heavy rifle with the same force. Which rifle will hurt the shoulder more and why ? (CBSE 2012)
Answer:
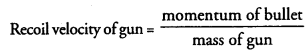
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 2
Recoil velocity of light rifle is more than that of heavy rifle. Therefore, light rifle will
hurt the shoulder more than heavy rifle.

Question 12.
A horse continues to apply a force in order to move a cart with a constant velocity. Explain why ?
Answer:
The cart will move with a constant velocity if no net external force acts on it. When horse applies a force on the cart, frictional force, also acts between the tyres of the cart and the road to oppose its motion. The cart will move with constant velocity only if the force applied by the horse is equal to the frictional force.

Question 13.
A ball of mass m is thrown vertically upward with an initial speed Its speed decreases continuously till it becomes zero. Thereafter, the ball begins to fell downward and attains the speed v again before striking the ground. It implies that the magnitude of initial and final momentum of the ball are same. Yet, it is not example of conservation of momentum. Explain why ?
(CBSE Sample Paper)
Answer:
Momentum of the system is conserved only if no external force acts on the system. However, in the given example, gravitational force acts on the ball when it moves upward or when it falls downward. Therefore, it is not the example of conservation of momentum.

Question 14.
Velocity versus time graph of a ball of mass 50 g rolling on a concrete floor is shown in Fig. 1
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 3
Calculate the acceleration and frictional force of the floor on the ball.
Answer:
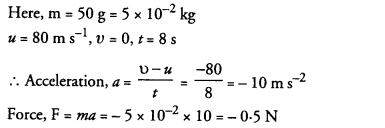
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 4
This force is known as retarding force or the frictional force of the floor on the ball.

Question 15.
A truck of mass M is moved under a force F. If the truck is then loaded with an object equal to the mass of the truck and the driving force is halved, then how does the acceleration change ?
Answer:
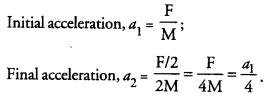
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 5

Question 16.
Two friends on roller-skates are standing 5 metres apart facing each other. One of them throws a ball of 2 kg towards the other, who catches it. How will this activity affect the position of the two ? Explain.
Answer:
When one boy throws a ball towards the other boy, he moves in the backward direction to conserve the linear momentum. On the other hand, the second boy will move away from the first boy after receiving momentum from the ball. Therefore, the distance between two friends will increase.

Question 17.
Water sprinkler used for grass lawns begins to rotate as soon as the water is supplied. Explain the principle on which it works.
Answer:
Water sprinkler works on Newton’s third law of motion.

LONG ANSWER QUESTIONS

Question 18.
Using second law of motion, derive the relation between force and acceleration. A bullet of 10 g strikes a sand-bag at a speed of 103 ms-1 and gets embedded after travelling 5 cm. Calculate
(i) the resistive force exerted by the sand on the bullet
(ii) the time taken by the bullet to come to rest.
Answer:
According to this law, the change in momentum of a body per unit time (i.e. rate of change of momentum) is directly proportional to the unbalanced force acting on the body and the change in momentum takes place in the direction of the unbalanced force on the body.
Consider a body of mass moving with initial velocity Let a force acts on the body for time so that the velocity of the body after time is .
Initial momentum of the body, pi = mu
Final momentum of the body, pf = mv
Now, change in momentum of the body = pf — pi = mv – mu = m(v-u)
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 6
Thus, force acting on the body is directly proportional to (i) its mass (m) and (ii) its acceleration (a).
Eqn. (1) gives the mathematical form of Newtons second law of motion. The force given by eqn (1) acts on the body.
Newton’s second law of motion in vector form     
We know, force ( F ) and acceleration ( a ) are vector quantities, whereas mass ( m)  is a scalar quantity. Therefore, Newton’s second law of motion can be written in vector form as
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 7
This relation shows that the direction of force applied on the body is same as that of the acceleration produced in the body.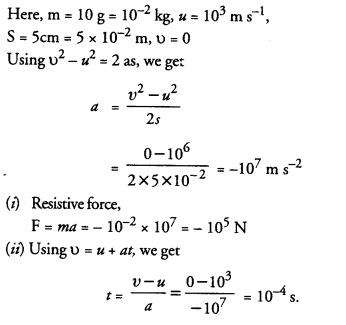NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 8

Question 19.
Derive the unit of force using the second law of motion. A force of 5 N produces an acceleration of 8 m s-2 on a mass m1 and an acceleration of 24 m s-2 on a mass m2. What acceleration would the same force provide if both the masses are tied together ?
Answer:
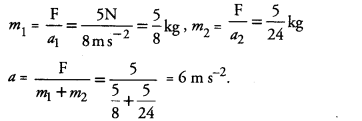
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 9

Question 20.
What is momentum ? Write its SI unit. Interpret force in terms of momentum. Represent the following graphically
(a) momentum versus velocity when mass is fixed.
(b) momentum versus mass when velocity is constant.
Answer:
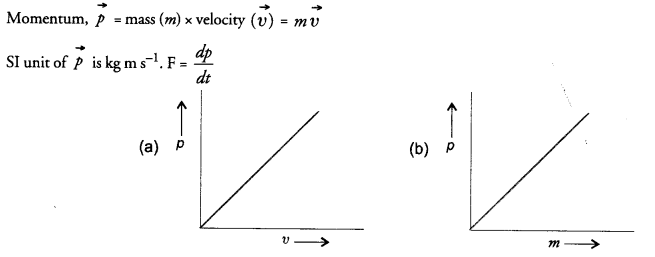
NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion image - 10

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS

by

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS

Other Exercises

Question 1.
In the figure, two circles intersect at A and B. The centre of the smaller circle is O and it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q1.1
Solution:
Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴ ∠AOB = 2∠APB = 2 x 70° = 140°
Now in cyclic quadrilateral AOBC,
∠AOB + ∠ACB = 180° (Sum of the angles)
⇒ 140° +∠ACB = 180°
⇒ ∠ACB = 180° – 140° = 40°
∴ ∠ACB = 40°

Question 2.
In the figure, two congruent circles with centre O and O’ intersect at A and B. If ∠AO’B = 50°, then find ∠APB.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q2.1
Solution:
Two congruent circles with centres O and O’ intersect at A and B
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q2.2
∠AO’B = 50°
∵ OA = OB = O’A = 04B (Radii of the congruent circles)
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q2.3

Question 3.
In the figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = IT, AC and BD intersect at P. Then, find ∠DPC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q3.1
Solution:
∵ ABCD is a cyclic quadrilateral,
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q3.2
∴ ∠BAD + ∠BCD = 180°
⇒ 75° + ∠BCD – 180°
⇒ ∠BCD = 180°-75°= 105° and ∠ADC + ∠ABC = 180°
⇒ 77° + ∠ABC = 180°
⇒ ∠ABC = 180°-77°= 103°
∴ ∠DBC = ∠ABC – ∠ABD = 103° – 58° = 45°
∵ Arc AD subtends ∠ABD and ∠ACD in the same segment of the circle 3
∴ ∠ABD = ∠ACD = 58°
∴ ∠ACB = ∠BCD – ∠ACD = 105° – 58° = 47°
Now in ∆PBC,
Ext. ∠DPC = ∠PBC + ∠PCB
=∠DBC + ∠ACB = 45° + 47° = 92°
Hence ∠DPC = 92°

Question 4.
In the figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q4.1
Solution:
In the figure, ∠AOB = 80°, ∠ABC = 30°
∵ Arc AB subtends ∠AOB at the centre and
∠ACB at the remaining part of the circle
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q4.2
∴ ∠ACB = \(\frac { 1 }{ 2 }\)∠AOB = \(\frac { 1 }{ 2 }\) x 80° = 40°
In ∆OAB, OA = OB
∴ ∠OAB = ∠OBA
But ∠OAB + ∠OBA + ∠AOB = 180°
∴ ∠OAB + ∠OBA + 80° = 180°
⇒ ∠OAB + ∠OAB = 180° – 80° = 100°
∴ 2∠OAB = 100°
⇒ ∠OAB = \(\frac { { 100 }^{ \circ } }{ 2 }\)  = 50°
Similarly, in ∆ABC,
∠BAC + ∠ACB + ∠ABC = 180°
∠BAC + 40° + 30° = 180°
⇒ ∠BAC = 180°-30°-40°
= 180°-70°= 110°
∴ ∠CAO = ∠BAC – ∠OAB
= 110°-50° = 60°

Question 5.
In the figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q5.1
Solution:
In the figure, ABCD is a parallelogram and
CDE is a straight line
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q5.2
∵ ABCD is a ||gm
∴ ∠A = ∠C
and ∠C = ∠ADE (Corresponding angles)
⇒ ∠BCD = ∠ADE
Similarly, ∠ABE = ∠BED (Alternate angles)
∵ arc BD subtends ∠BAD at the centre and
∠BED at the remaining part of the circle
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q5.3

Question 6.
In the figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q6.1
Solution:
In the figure, AB is the diameter of the circle such that ∠A = 35° and ∠Q = 25°, join OP.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q6.2
Arc PB subtends ∠POB at the centre and
∠PAB at the remaining part of the circle
∴ ∠POB = 2∠PAB = 2 x 35° = 70°
Now in ∆OP,
OP = OB radii of the circle
∴ ∠OPB = ∠OBP = 70° (∵ ∠OPB + ∠OBP = 140°)
Now ∠APB = 90° (Angle in a semicircle)
∴ ∠BPQ = 90°
and in ∆PQB,
Ext. ∠PBR = ∠BPQ + ∠PQB
= 90° + 25°= 115°
∴ ∠PBR = 115°

Question 7.
In the figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q7.1
Solution:
In the figure, P and Q are the centres of two circles which intersect each other at C and B
ACD is a straight line ∠APB = 150°
Arc AB subtends ∠APB at the centre and
∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠APB = \(\frac { 1 }{ 2 }\) x 150° = 75°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 75° + ∠BCD = 180°
∠BCD = 180°-75°= 105°
Now arc BD subtends reflex ∠BQD at the centre and ∠BCD at the remaining part of the circle
Reflex ∠BQD = 2∠BCD = 2 x 105° = 210°
But ∠BQD + reflex ∠BQD = 360°
∴ ∠BQD+ 210° = 360°
∴ ∠BQD = 360° – 210° = 150°

Question 8.
In the figure, if O is circumcentre of ∆ABC then find the value of ∠OBC + ∠BAC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q8.1
Solution:
In the figure, join OC
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q8.2
∵ O is the circumcentre of ∆ABC
∴ OA = OB = OC
∵ ∠CAO = 60° (Proved)
∴ ∆OAC is an equilateral triangle
∴ ∠AOC = 60°
Now, ∠BOC = ∠BOA + ∠AOC
= 80° + 60° = 140°
and in ∆OBC, OB = OC
∠OCB = ∠OBC
But ∠OCB + ∠OBC = 180° – ∠BOC
= 180°- 140° = 40°
⇒ ∠OBC + ∠OBC = 40°
∴ ∠OBC = \(\frac { { 40 }^{ \circ } }{ 2 }\)  = 20°
∠BAC = OAB + ∠OAC = 50° + 60° = 110°
∴ ∠OBC + ∠BAC = 20° + 110° = 130°

Question 9.
In the AOC is a diameter of the circle and arc AXB = 1/2 arc BYC. Find ∠BOC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q9.1
Solution:
In the figure, AOC is diameter arc AxB = \(\frac { 1 }{ 2 }\) arc BYC 1
∠AOB = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠AOB
But ∠AOB + ∠BOC = 180°
⇒ ∠AOB + 2∠AOB = 180°
⇒ 3 ∠AOB = 180°
∴ ∠AOB = \(\frac { { 180 }^{ \circ } }{ 3 }\)  = 60°
∴ ∠BOC = 2 x 60° = 120°

Question 10.
In the figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q10.1
Solution:
In the figure, ABCD is a cyclic quadrilateral
CD is produced to E such that ∠ADE = 95°
O is the centre of the circle
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS Q10.2
∵ ∠ADC + ∠ADE = 180°
⇒ ∠ADC + 95° = 180°
⇒ ∠ADC = 180°-95° = 85°
Now arc ABC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle
∵ ∠AOC = 2∠ADC = 2 x 85° = 170°
Now in ∆OAC,
∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ ∠OAC = ∠OCA (∵ OA = OC radii of circle)
∴ ∠OAC + ∠OAC + 170° = 180°
2∠OAC = 180°- 170°= 10°
∴ ∠OAC = \(\frac { { 10 }^{ \circ } }{ 2 }\) = 5°

 

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

 

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B

by

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B.

Other Exercises

Question 1.
Solution:
∵ x and y are inversely proportional
Then xy are equal
(i) xy = 6 x 9 = 54
= 10 x 15 = 150
= 14 x 21 = 294
= 16 x 24 = 384
∵ xy in each case is not equal
So, x and y are not inversely proportional
(ii) xy = 5 x 18 = 90
= 9 x 10 = 90
= 15 x 6 = 90
= 3 x 30 = 90
= 45 x 2 = 90
∵ xy in each case is equal
x and y are inversely proportional
(iii) xy = 9 x 4 = 36
= 3 x 12 = 36
= 6 x 9 = 54
= 36 x 1 = 36
∵ xy in each is not equal
x and y are not inversely proportional

You can also Download NCERT Solutions for Class 8 English to help you to revise complete Syllabus and score more marks in your examinations.

Question 2.
Solution:
x and y are inversely proportional
xy is equal
Now,
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 2.1

Question 3.
Solution:
Let required number of days = x
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 3.1

Question 4.
Solution:
A pond is! dug in 8 days by = 12 men
It can be dug in 1 day by = 12 x 8 men (Less days, more men)
and it can be dug in 6 days by = \(\\ \frac { 12X8 }{ 6 } \)
= 16 men Ans. (more days, less men)

Question 5.
Solution:
Let 14 cows can graze in x days
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 5.1

Question 6.
Solution:
Let required time take = x hour
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 6.1
By inverse proportion
60 : x :: 75 : 5
x = \(\\ \frac { 50X5 }{ 75 } \)
Time required = 4 hours

Question 7.
Solution:
Let machines required = x
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 7.1

Question 8.
Solution:
Let 8 taken will fill in tank in x hour
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 8.1

Question 9.
Solution:
8 taps can fill tank in = 27 minutes
1 tap can fill that tank in = 27 x 8 minutes (less tap, more time)
8 – 2 = 6 taps can fill that tank in
= \(\\ \frac { 27X8 }{ 6 } \) minutes
= 36 minutes

Question 10.
Solution:
Let total animals can be feed with food in x days
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 10.1

Question 11.
Solution:
Let for x day, the food provision is sufficient for 900 + 500 = 1400 men
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 11.1

Question 12.
Solution:
Let the food will be for x days
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 12.1

Question 13.
Solution:
Let each period will be of x minutes
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B 13.1

Question 14.
Solution:
x and y are inversely
and x = 15, y = 6
Then xy = 15 x 6 = 90
Now if x = 9, then y = \(\\ \frac { 90 }{ 9 } \)
= 10

Question 15.
Solution:
x and y are inversely and x = 18, y = 8
xy = 18 x 8 = 144
Now if y = 16,
then x = \(\\ \frac { 144 }{ 16 } \)
= 9

Hope given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A

by

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A.

Other Exercises

Question 1.
Solution:
(i) \(\\ \frac { x }{ y } \) = \(\\ \frac { 3 }{ 9 } \) = \(\\ \frac { 1 }{ 3 } \)
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 1.1
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 1.2
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 1.3

Question 2.
Solution:
x and y are directly proportional
\(\\ \frac { x }{ y } \) = \(\\ \frac { 3 }{ 72 } \) = \(\\ \frac { 1 }{ 24 } \)
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 2.1

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 3.1

Question 4.
Solution:
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 4.1

Question 5.
Solution:
Let distance covered = x then
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 5.1

Question 6.
Solution:
Let no. of dolls = x, then
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 6.1

Question 7.
Solution:
Let x kg of sugar will be bought
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 7.1

Question 8.
Solution:
Let cloth bought = x m
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 8.1

Question 9.
Solution:
Let length of model ship = x m
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 9.1

Question 10.
Solution:
Let x kg dust will be picked up
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 10.1

Question 11.
Solution:
A speed of car = 50 km/hr
Distance travelled in 1 hr. = 5 m
Let required distance travelled in 1 hr. 12 min.
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 11.1

Question 12.
Solution:
Let required distance covered = x km
Speed of man = 5 km/hr
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 12.1

Question 13.
Solution:
Let required thickness = x mm
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 13.1

Question 14.
Solution:
Let men required = x
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 14.1

Question 15.
Solution:
Let no. of words type in 8 minutes = x
RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A 15.1

 

Hope given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

by

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

Other Exercises

Question 1.
In the figure, ∆ABC is an equilateral triangle. Find m ∠BEC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q1.1
Solution:
∵ ∆ABC is an equilateral triangle
∴ A = 60°
∵ ABEC is a cyclic quadrilateral
∴ ∠A + ∠E = 180° (Sum of opposite angles)
⇒ 60° + ∠E = 180°
⇒ ∠E = 180° – 60° = 120°
∴ m ∠BEC = 120°

Question 2.
In the figure, ∆PQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q2.1
Solution:
In the figure, ∆PQR is an isosceles PQ = PR
∠PQR = 35°
∴ ∠PRQ = 35°
But ∠PQR + ∠PRQ + ∠QPR = 180° (Sum of angles of a triangle)
⇒ 35° + 35° + ∠QPR = 180°
⇒ 70° + ∠QPR = 180°
∴ ∠QPR = 180° – 70° = 110°
∵ ∠QSR = ∠QPR (Angle in the same segment of circles)
∴ ∠QSR = 110°
But PQTR is a cyclic quadrilateral
∴ ∠QTR + ∠QPR = 180°
⇒ ∠QTR + 110° = 180°
⇒ ∠QTR = 180° -110° = 70°
Hence ∠QTR = 70°

Question 3.
In the figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q3.1
Solution:
In the figure, O is the centre of the circle ∠BOD =160°
ABCD is the cyclic quadrilateral
∵ Arc BAD subtends ∠BOD is the angle at the centre and ∠BCD is on the other part of the circle
∴ ∠BCD = \(\frac { 1 }{ 2 }\) ∠BOD
⇒ x = \(\frac { 1 }{ 2 }\) x 160° = 80°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ y + x = 180°
⇒ y + 80° = 180°
⇒ y =180°- 80° = 100°
∴ x = 80°, y = 100°

Question 4.
In the figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q4.1
Solution:
In a circle, ABCD is a cyclic quadrilateral ∠BCD = 100° and ∠ABD = 70°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180° (Sum of opposite angles)
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q4.2
⇒ ∠A + 100°= 180°
∠A = 180°- 100° = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180°
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
∴ ∠ADB = 180°- 150° = 30°
Hence ∠ADB = 30°

Question 5.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q5.1
Solution:
Given : ABCD is a cyclic quadrilateral in which AD || BC
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q5.2
To prove : ∠B = ∠C
Proof : ∵ AD || BC
∴ ∠A + ∠B = 180°
(Sum of cointerior angles)
But ∠A + ∠C = 180°
(Opposite angles of the cyclic quadrilateral)
∴ ∠A + ∠B = ∠A + ∠C
⇒ ∠B = ∠C
Hence ∠B = ∠C

Question 6.
In the figure, O is the centre of the circle. Find ∠CBD.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q6.1
Solution:
Arc AC subtends ∠AOC at the centre and ∠APC at the remaining part of the circle
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q6.2
∴ ∠APC = \(\frac { 1 }{ 2 }\) ∠AOC
= \(\frac { 1 }{ 2 }\) x 100° = 50°
∵ APCB is a.cyclic quadrilateral,
∴ ∠APC + ∠ABC = 180°
⇒ 50° + ∠ABC = 180° ⇒ ∠ABC =180°- 50°
∴ ∠ABC =130°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 130° + ∠CBD = 180°
⇒ ∠CBD = 180°- 130° = 50°
∴ ∠CBD = 50°

Question 7.
In the figure, AB and CD are diameiers of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q7.1
Solution:
Two diameters AB and CD intersect each other at O. AC, CB and BD are joined
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q7.2
∠DBA = 50°
∠DBA and ∠DCA are in the same segment
∴ ∠DBA = ∠DCA = 50°
In ∆OAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠DCA = 50°
and ∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ 50° + 50° + ∠AOC = 180°
⇒ 100° + ∠AOC = 180°
⇒ ∠AOC = 180° – 100° = 80°
Hence ∠AOC = 80°

Question 8.
On a semi circle with AB as diameter, a point C is taken so that m (∠CAB) = 30°. Find m (∠ACB) and m (∠ABC).
Solution:
A semicircle with AB as diameter
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q8.1
∠ CAB = 30°
∠ACB = 90° (Angle in a semi circle)
But ∠CAB + ∠ACB + ∠ABC = 180°
⇒ 30° + 90° + ∠ABC – 180°
⇒ 120° + ∠ABC = 180°
∴ ∠ABC = 180°- 120° = 60°
Hence m ∠ACB = 90°
and m ∠ABC = 60°

Question 9.
In a cyclic quadrilateral ABCD, if AB || CD and ∠B = 70°, find the remaining angles.
Solution:
In a cyclic quadrilateral ABCD, AB || CD and ∠B = 70°
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q9.1
∵ ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ 70° + ∠D = 180°
⇒ ∠D = 180°-70° = 110°
∵ AB || CD
∴ ∠A + ∠D = 180° (Sum of cointerior angles)
∠A+ 110°= 180°
⇒ ∠A= 180°- 110° = 70°
Similarly, ∠B + ∠C = 180°
⇒ 70° + ∠C- 180° ‘
⇒ ∠C = 180°-70°= 110°
∴ ∠A = 70°, ∠C = 110°, ∠D = 110°

Question 10.
In a cyclic quadrilateral ABCD, if m ∠A = 3(m ∠C). Find m ∠A.
Solution:
In cyclic quadrilateral ABCD, m ∠A = 3(m ∠C)
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q10.1
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ 3 ∠C + ∠C = 180° ⇒ 4∠C = 180°
⇒ ∠C = \(\frac { { 180 }^{ \circ } }{ 4 }\)  = 45°
∴ ∠A = 3 x 45°= 135°
Hence m ∠A =135°

Question 11.
In the figure, O is the centre of the circle and ∠DAB = 50°. Calculate the values of x and y.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q11.1
Solution:
In the figure, O is the centre of the circle ∠DAB = 50°
∵ ABCD is a cyclic quadrilateral
∴ ∠A + ∠C = 180°
⇒ 50° + y = 180°
⇒ y = 180° – 50° = 130°
In ∆OAB, OA = OB (Radii of the circle)
∴ ∠A = ∠OBA = 50°
∴ Ext. ∠DOB = ∠A + ∠OBA
x = 50° + 50° = 100°
∴ x= 100°, y= 130°

Question 12.
In the figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q12.1
Solution:
In ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q12.2
60° + ∠ABC + 20° = 180°
∠ABC + 80° = 180°
∴ ∠ABC = 180° -80°= 100°
∵ ABCD is a cyclic quadrilateral,
∴ ∠ABC + ∠ADC = 180°
100° + ∠ADC = 180°
∴ ∠ADC = 180°- 100° = 80°

Question 13.
In the figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q13.1
Solution:
In a circle, ∆ABC is an equilateral triangle
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q13.2
∴ ∠A = 60°
∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 60°
∵ BECD is a cyclic quadrilateral
∴ ∠BDC + ∠BEC = 180°
⇒ 60° + ∠BEC = 180°
⇒ ∠BEC = 180°-60°= 120°
Hence ∠BDC = 60° and ∠BEC = 120°

Question 14.
In the figure, O is the centre of the circle. If ∠CEA = 30°, find the values of x, y and z.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q14.1
Solution:
∠AEC and ∠ADC are in the same segment
∴ ∠AEC = ∠ADC = 30°
∴ z = 30°
ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ x + z = 180°
⇒ x + 30° = 180°
⇒ x = 180° – 30° = 150°
Arc AC subtends ∠AOB at the centre and ∠ADC at the remaining part of the circle
∴ ∠AOC = 2∠D = 2 x 30° = 60°
∴ y = 60°
Hence x = 150°, y – 60° and z = 30°

Question 15.
In the figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q15.1
Solution:
In the figure, two circles intersect each other at C and D
∠BAD = 78°, ∠DCF = x, ∠DEF = y
ABCD is a cyclic quadrilateral
∴ Ext. ∠DCF = its interior opposite ∠BAD
⇒ x = 78°
In cyclic quadrilateral CDEF,
∠DCF + ∠DEF = 180°
⇒ 78° + y = 180°
⇒ y = 180° – 78°
y = 102°
Hence x = 78°, and y- 102°

Question 16.
In a cyclic quadrilateral ABCD, if ∠A – ∠C = 60°, prove that the smaller of two is 60°.
Solution:
In cyclic quadrilateral ABCD,
∠A – ∠C = 60°
But ∠A + ∠C = 180° (Sum of opposite angles)
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q16.1
Adding, 2∠A = 240° ⇒ ∠A = \(\frac { { 62 }^{ \circ } }{ 2 }\)  = 120° and subtracting
2∠C = 120° ⇒ ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\)  = 60°
∴ Smaller angle of the two is 60°.

Question 17.
In the figure, ABCD is a cyclic quadrilateral. Find the value of x.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q17.1
Solution:
∠CDE + ∠CDA = 180° (Linear pair)
⇒ 80° + ∠CDA = 180°
⇒ ∠CDA = 180° – 80° = 100°
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q17.2
In cyclic quadrilateral ABCD,
Ext. ∠ABF = Its interior opposite angle ∠CDA = 100°
∴ x = 100°

Question 18.
ABCD is a cyclic quadrilateral in which:
(i) BC || AD, ∠ADC =110° and ∠B AC = 50°. Find ∠DAC.
(ii) ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
(iii) ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.
Solution:
(i) In the figure,
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q18.1
ABCD is a cyclic quadrilateral and AD || BC, ∠ADC = 110°
∠BAC = 50°
∵ ∠B + ∠D = 180° (Sum of opposite angles)
⇒ ∠B + 110° = 180°
∴ ∠B = 180°- 110° = 70°
Now in ∆ABC,
∠CAB + ∠ABC + ∠BCA = 180° (Sum of angles of a triangle)
⇒ 50° + 70° + ∠BCA = 180°
⇒ 120° + ∠BCA = 180°
⇒ ∠BCA = 180° – 120° = 60°
But ∠DAC = ∠BCA (Alternate angles)
∴ ∠DAC = 60°
(ii) In cyclic quadrilateral ABCD,
Diagonals AC and BD are joined ∠DBC = 80°, ∠BAC = 40°
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q18.2
Arc DC subtends ∠DBC and ∠DAC in the same segment
∴ ∠DBC = ∠DAC = 80°
∴ ∠DAB = ∠DAC + ∠CAB = 80° + 40° = 120°
But ∠DAC + ∠BCD = 180° (Sum of opposite angles of a cyclic quad.)
⇒ 120° +∠BCD = 180°
⇒ ∠BCD = 180°- 120° = 60°
(iii) In the figure, ABCD is a cyclic quadrilateral BD is joined
∠BCD = 100°
and ∠ABD = 70°
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q18.3
∠A + ∠C = 180° (Sum of opposite angles of cyclic quad.)
∠A+ 100°= 180°
⇒ ∠A= 180°- 100°
∴ ∠A = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
⇒ ∠ADB = 180°- 150° = 30°
∴ ∠ADB = 30°

Question 19.
Prove that the circles described on the four sides of a rhombus as diameter, pass through the point of intersection of its diagonals.
Solution:
Given : ABCD is a rhombus. Four circles are drawn on the sides AB, BC, CD and DA respectively
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q19.1
To prove : The circles pass through the point of intersection of the diagonals of the rhombus ABCD
Proof: ABCD is a rhombus whose diagonals AC and BD intersect each other at O
∵ The diagonals of a rhombus bisect each other at right angles
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Now when ∠AOB = 90°
and a circle described on AB as diameter will pass through O
Similarly, the circles on BC, CD and DA as diameter, will also pass through O

Question 20.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that is diagonals are equal.
Solution:
Given : In cyclic quadrilateral ABCD, AB = CD
AC and BD are the diagonals
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q20.1
To prove : AC = BC
Proof: ∵ AB = CD
∴ arc AB = arc CD
Adding arc BC to both sides, then arc AB + arc BC = arc BC + arc CD
⇒ arc AC = arc BD
∴ AC = BD
Hence diagonal of the cyclic quadrilateral are equal.

Question 21.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Solution:
Given : In ∆ABC, circles are drawn on sides AB and AC
To prove : Circles drawn on AB and AC intersect at D which lies on BC, the third side
Construction : Draw AD ⊥ BC
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q21.1
Proof: ∵ AD ⊥ BC
∴ ∠ADB = ∠ADC = 90°
So, the circles drawn on sides AB and AC as diameter will pass through D
Hence circles drawn on two sides of a triangle pass through D, which lies on the third side.

Question 22.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Solution:
In the figure, ABCD is a trapezium in which AD || BC and ∠B = 70°
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q22.1
∵ AD || BC
∴ ∠A + ∠B = 180° (Sum of cointerior angles)
⇒ ∠A + 70° = 180°
⇒ ∠A= 180°- 70° = 110°
∴ ∠A = 110°
But ∠A + ∠C = 180° and ∠B + ∠D = 180° (Sum of opposite angles of a cyclic quadrilateral)
∴ 110° + ∠C = 180°
⇒ ∠C = 180°- 110° = 70°
and 70° + ∠D = 180°
⇒ ∠D = 180° – 70° = 110°
∴ ∠A = 110°, ∠C = 70° and ∠D = 110°

Question 23.
In the figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q23.1
Solution:
In the figure, ABCD is a cyclic quadrilateral whose diagonals AC and BD are drawn ∠DBC = 55° and ∠BAC = 45°
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q23.2
∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 45°
Now in ABCD,
∠DBC + ∠BDC + ∠BCD = 180° (Sum of angles of a triangle)
⇒ 55° + 45° + ∠BCD = 180°
⇒ 100° + ∠BCD = 180°
⇒ ∠BCD = 180° – 100° = 80°
Hence ∠BCD = 80°

Question 24.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Solution:
Given : ABCD is a cyclic quadrilateral
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q24.1
To prove : The perpendicular bisectors of the sides are concurrent
Proof : ∵ Each side of the cyclic quadrilateral is a chord of the circle and perpendicular of a chord passes through the centre of the circle
Hence the perpendicular bisectors of each side will pass through the centre O
Hence the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent

Question 25.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
Solution:
Given : ABCD is a cyclic rectangle and diagonals AC and BD intersect each other at O
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q25.1
To prove : O is the point of intersection is the centre of the circle.
Proof : Let O be the centre of the circle- circumscribing the rectangle ABCD
Since each angle of a rectangle is a right angle and AC is the chord of the circle
∴ AC will be the diameter of the circle Similarly, we can prove that diagonal BD is also the diameter of the circle
∴ The diameters of the circle pass through the centre
Hence the point of intersection of the diagonals of the rectangle is the centre of the circle.

Question 26.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that:
(i) AD || BC
(ii) EB = EC.
Solution:
Given : ABCD is a cyclic quadrilateral in which sides BA and CD are produced to meet at E and EA = ED
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q26.1
To prove :
(i) AD || BC
(ii) EB = EC
Proof: ∵ EA = ED
∴ In ∆EAD
∠EAD = ∠EDA (Angles opposite to equal sides)
In a cyclic quadrilateral ABCD,
Ext. ∠EAD = ∠C
Similarly Ext. ∠EDA = ∠B
∵ ∠EAD = ∠EDA
∴ ∠B = ∠C
Now in ∆EBC,
∵ ∠B = ∠C
∴ EC = EB (Sides opposite to equal sides)
and ∠EAD = ∠B
But these are corresponding angles
∴ AD || BC

Question 27.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Solution:
Given : A segment ACB shorter than a semicircle and an angle ∠ACB inscribed in it
To prove : ∠ACB < 90°
Construction : Join OA and OB
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q27.1
Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle ∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB But ∠AOB > 180° (Reflex angle)
∴ ∠ACB > \(\frac { 1 }{ 2 }\) x [80°
⇒ ∠ACB > 90°

Question 28.
Prove that the angle in a segment greater than a semi-circle is less than a right angle
Solution:
Given : A segment ACB, greater than a semicircle with centre O and ∠ACB is described in it
To prove : ∠ACB < 90°
Construction : Join OA and OB
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q28.1
Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠ACB =\(\frac { 1 }{ 2 }\) ∠AOB
But ∠AOB < 180° (A straight angle) 1
∴ ∠ACB < \(\frac { 1 }{ 2 }\) x 180°
⇒ ∠ACB <90°
Hence ∠ACB < 90°

Question 29.
Prove that the line segment joining the mid-point of the hypotenuse of a rijght triangle to its opposite vertex is half of the hypotenuse.
Solution:
Given : In a right angled ∆ABC
∠B = 90°, D is the mid point of hypotenuse AC. DB is joined.
To prove : BD = \(\frac { 1 }{ 2 }\) AC
Construction : Draw a circle with centre D and AC as diameter
RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 Q29.1
Proof: ∵ ∠ABC = 90°
∴ The circle drawn on AC as diameter will pass through B
∴ BD is the radius of the circle
But AC is the diameter of the circle and D is mid point of AC
∴ AD = DC = BD
∴ BD= \(\frac { 1 }{ 2 }\) AC

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.