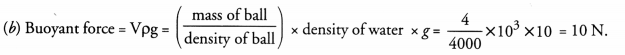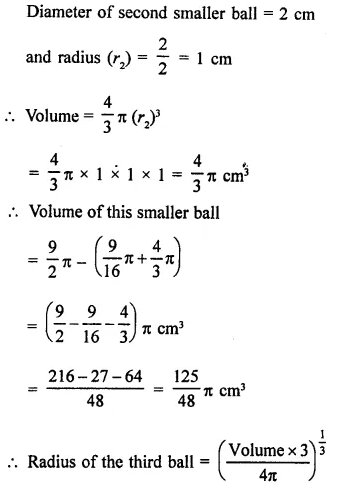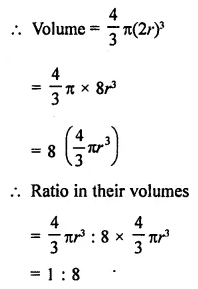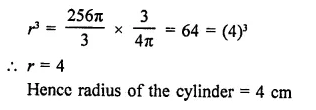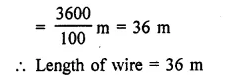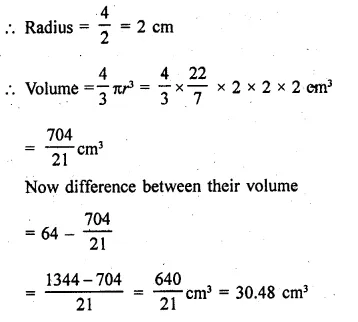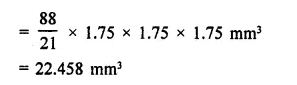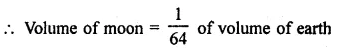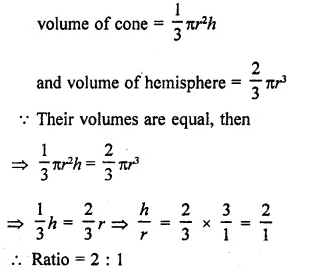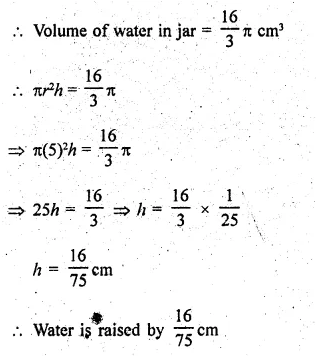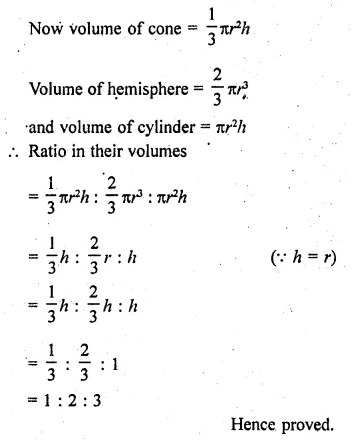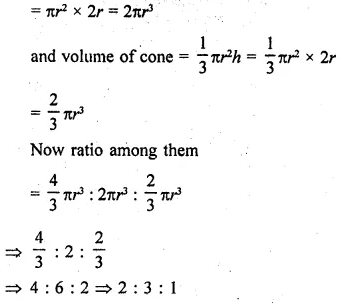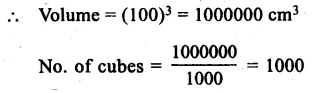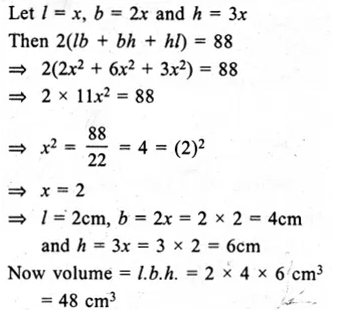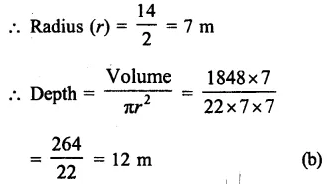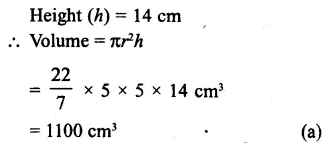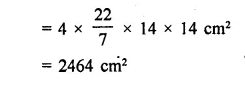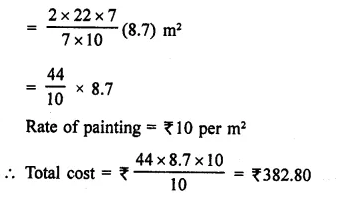Prasanna – Page 953 – MCQ Questions

NCERT Exemplar Solutions for Class 9 Science Chapter 16 Floatation

January 5, 2022July 6, 2018 by Prasanna

NCERT Exemplar Solutions for Class 9 Science Chapter 16 Floatation

These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 16 Floatation

MULTIPLE CHOICE QUESTIONS

Question 1.
An object is put one by one in three liquids having different densities. The object floats with 1/9, 2/11 and 3/7 parts of their volumes outside the liquid surface in liquids of densities d₁, d₂ and d₃ respectively. Which of the following statement is correct ?
(a) d₁ > d₂> d₃
(b) d₁ > d₂< d₃
(c) d₁< d₂> d₃
(d) d₁ < d₂< d₃
Answer:
(d). Upthrust due to liquid on an object is directly proportional to the density of the liquid.

More Resources

Question 2.
An obj ect weighs 10 N in air. When immersed fully in water, it weighs only 8 N. The weight of the liquid displaced by the object will be
(a) 2 N
(b) 8 N
(c) 10 N
(d) 12 N.
Answer:
(a). Explanation : Weight of liquid displaced by an object = Weight of object in air – weight in liquid.

Question 3.
A girl stands on a box having 60 cm length, 40 cm breadth and 20 cm width in three ways. In which of the following cases, pressure exerted by the brick will be
(a) maximum when length and breadth form the base
(b) maximum when breadth and width form the base
(c) maximum when width and length form the base
(d) the same in all the above three cases.
Answer:
(b). Explanation :

SHORT ANSWER QUESTIONS

Question 4.
(a) A cube of side 5 cm is immersed in water and then in saturated salt solution. In which case will it experience a greater buoyant force.
If each side of the cube is reduced to 4 cm and then immersed in water, what will be the effect on the buoyant force experienced by the cubeas compared to the first case for water. Give reason for each case. (CBSE 2012)
(b) A ball weighing 4 kg of density 4000 kg m^-3 is completely immersed in water of density 10³ kg m^-3. Find the force of buoyancy on it. (Given g = 10 ms^-2.)
Answer:
(a) Buoyant force = Vρg. Since, density (ρ) of saturated salt solution is more than that of water. So, the cube will experience greater buoyant force in saturated salt solution. When size of cube is reduced, its volume (V) also reduces. Hence, it will experience less buoyant force then in first case.
NCERT Exemplar Solutions for Class 9 Science Chapter 16 Floatation image - 2

Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 16 Floatation are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 21 Data Handling Ex 21A

January 5, 2022July 6, 2018 by Prasanna

RS Aggarwal Class 8 Solutions Chapter 21 Data Handling Ex 21A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 21 Data Handling Ex 21A.

Other Exercises

Question 1.
Solution:
RS Aggarwal Class 8 Solutions Chapter 21 Data Handling Ex 21A 1.1

Question 2.
Solution:
RS Aggarwal Class 8 Solutions Chapter 21 Data Handling Ex 21A 2.1

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 21 Data Handling Ex 21A 3.1

Hope given RS Aggarwal Solutions Class 8 Chapter 21 Data Handling Ex 21A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2

January 5, 2022July 6, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2

Other Exercises

Question 1.
Find the volume of a sphere whose radius is
(i) 2 cm
(ii) 3.5 cm
(iii) 10.5 cm
Solution:
(i) Radius of sphere (r) = 2 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 1.1

Question 2.
Find the volume of a sphere whose diameter is,
(i) 14 cm
(ii) 3.5 dm
(iii) 2.1 m
Solution:
(i) Diameter of a sphere = 14 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 2.1

Question 3.
A hemspherical tank has inner radius of 2.8 m. Find its capacity in litres.
Solution:
Radius of hemispherical tank (r) = 2.8 m
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 3.1

Question 4.
A hemispherical bowl is made of steel 0.25 cm thick. The inside radius of the bowl is 5 cm. Find the volume of steel used in making the bowl.
Solution:
Thickness of steel = 0.25 cm = \(\frac { 1 }{ 4 }\)cm
Inside radius of the hemispherical bowl (r) = 5 cm
∴ Outer radius (R) = 5 + 0.25 = 5.25 cm
∴ Volume of the steel used = \(\frac { 1 }{ 4 }\)π(R³ – r³)
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 4.1

Question 5.
How many bullets can be made out of a cube of lead, whose edge measures 22 cm, each bullet being 2 cm in diameter?
Solution:
Edge of cube (r) = 22 cm
∴ Volume = a³ = (22)³ cm³
= 22 x 22 x 22 = 10648 cm³
Diameter of a bullet = 2 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 5.1

Question 6.
A shopkeeper has one laddoo of radius 5 cm. With the same material how many laddoos of radius 2.5 cm can be made?
Solution:
Radius of bigger laddoo (R) = 5 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 6.1

Question 7.
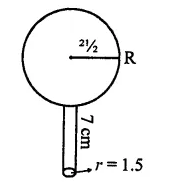
A spherical ball of lead 3 cm in diameter is melted and recast into three spherical balls. It the diameters of two balls be \(\frac { 3 }{ 2 }\) cm and 2 cm, find the diameter of the third ball.
Solution:
Diameter of a spherical ball of lead = 3 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 7.1

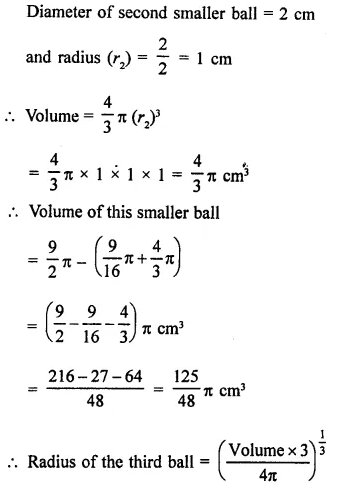
Question 8.
A sphere of radius 5 cm is immersed in water filled in a cylinder, the level of water rises \(\frac { 5 }{ 3 }\) cm. Find the radius of the cylinder.
Solution:
Radius of sphere (r1) = 5 cm
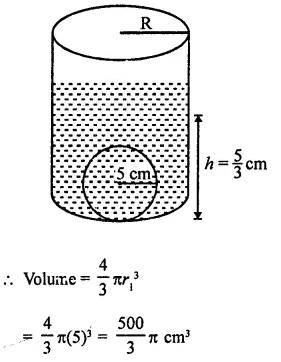
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 8.1
Level of water rises in the cylinder after immersing the sphere in it
∴ Height of water level = \(\frac { 5 }{ 3 }\) cm
Let r be radius of the cylinder, then Volume of water = Volume of the sphere

Question 9.
If the radius of a sphere is doubled, what is the ratio of the volumes of the first sphere to that of the second sphere?
Solution:
Let r2 be the radius of the given sphere
then volume = \(\frac { 4 }{ 3 }\) πr³
By doubling the radius the radius of the new sphere = 2r
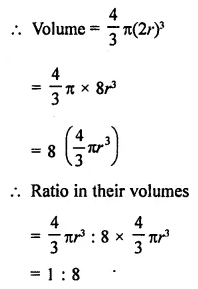
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 9.1

Question 10.
A vessel in the form of a hemispherical bowl is full of water. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.
Solution:
Radius of hemispherical bowl (r) = 3.5 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 10.1

Question 11.
A cylinder whose height is two thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
Solution:
Radius of a sphere (r) = 4 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 11.1

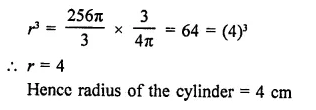
Question 12.
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder.
Solution:
Radius of hemispherical bowl (r) = 6 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 12.1

Question 13.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
Solution:
Diameter of a copper sphere = 18 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 13.1

Question 14.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Solution:
Diameter of a sphere = 6 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 14.1

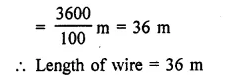
Question 15.
The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of height 2 \(\frac { 2 }{ 3 }\) cm. Find the diameter of the cylinder.
Solution:
Internal radius of the hollow spherical shell (r) = 3 cm
and external radius (R) = 5 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 15.1

Question 16.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere (r) = 7 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 16.1

Question 17.
A hollow sphere of internal and external radius 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
Solution:
Internal radius of a hollow sphere (r) = 2 cm
and external radius (R) = 4 cm
∴ Volume of the metal used
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 17.1

Question 18.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
Solution:
Radius of a metallic sphere (R) = 10.5 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 18.1

Question 19.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio Of their heights.
Solution:
Let r be the radius and h be the height of the cone, hemisphere
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 19.1

Question 20.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Solution:
By carving a largest sphere out of the cube, the diameter of the sphere = 10.5
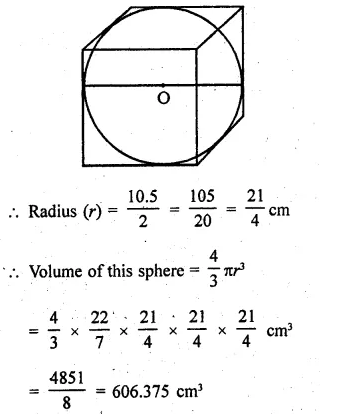
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 20.1

Question 21.
A cube, of side 4 cm, contains a sphere touching its sides. Find the volume of the gap in between.
Solution:
Side of cube = 4 cm
∴ Volume = (side)³ = 4x4x4 = 64 cm³
Diameter of the largest sphere touching its sides = 4 cm
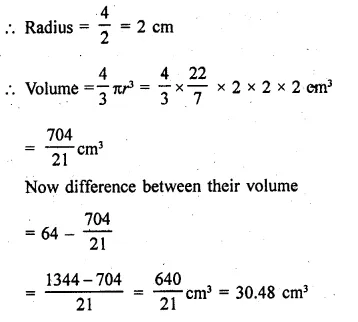
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 21.1

Question 22.
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1m, then find the volume of the iron used to make the tank. (NCERT)
Solution:
Thickness of hemispherical tank = 1 cm
Inner radius (r) = 1 m = 100 cm
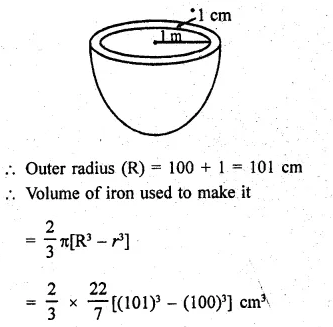
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 22.1

Question 23.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule? (NCERT)
Solution:
Diameter of a medicine spherical capsule = 3.5 mm
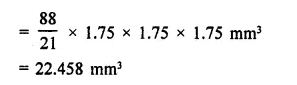
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 23.1

Question 24.
The diameter of the moon is approximately one fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon? (NCERT)
Solution:
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 24.1

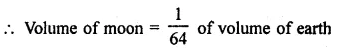
Question 25.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio in their heights.
Solution:
Let r be the radius of cone and hemisphere and let h be the height of the cone then
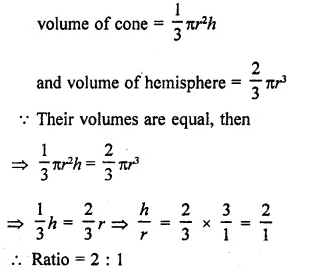
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 25.1

Question 26.
A cylindrical tub of radius 16 cm contains water to a depth of 30 cm. A spherical iron ball is dropped into the tub and thus level of water is raised by 9 cm. What is the radius of the ball?
Solution:
Radius of cylinderical tub (r) = 16 cm
Height of water in it (h) = 30 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 26.1

Question 27.
A cylinder of radius 12 cm contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. (Use π = 22/7).
Solution:
Radius of cylinder (r) = 12 cm
Depth of water in it (h) = 20 cm
By dropping a ball, the water level rose by 6.75 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 27.1

Question 28.
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres?
Solution:
Radius of cylinderical jar (r) = 6 cm
Level of oil in it (h) = 2 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 28.1

Question 29.
A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm eacfy are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
Solution:
Diameter of measuring jar = 10 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 29.1
Now after swing the ball in the water of jar Let volume of water raised, by h cm

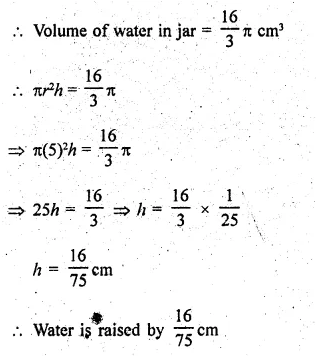
Question 30.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2:3.
Solution:
∵ Bases and heights of a cones hemisphere and a cylinder are equal
Let r be the radius and h be their heights
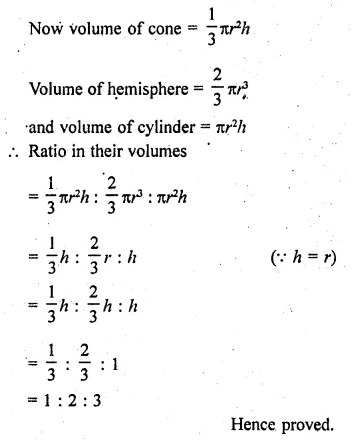
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 30.1

Question 31.
A cylinderical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball is dropped into the tub and thus the level of water is raised by 6.75 cm. What is the radius of the ball?
Solution:
Radius of the cylinderical tub (r) = 12 cm
Depth of water in it (h) = 20 cm
By dropping a spherical ball in it, the water raised by 6.75 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 31.1

Question 32.
A sphere, a cylinder and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. Find the ratio of their volumes.
Solution:
Diameter of a sphere, cylinder and a cone are equal
Let each as diameter = 2r
Then radius of each = r
Height of cylinder = diameter = 2r
and height of cone = 2r
Now volume of sphere = \(\frac { 4 }{ 3 }\)πr³
Volume of cylinder = πr²h
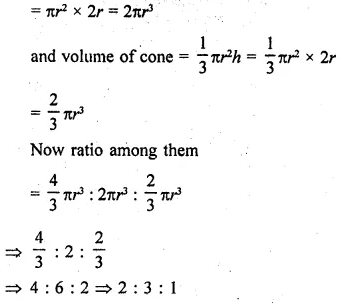
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 32.1

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C

January 5, 2022July 6, 2018 by Prasanna

RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C.

Other Exercises

Tick the correct answer in each of the following:

Question 1.
Solution:
Answer = (b)
Length (l) = 12 cm
Breadth (b) = 9cm
height (h) = 8 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 1.1

Question 2.
Solution:
Total surface area of cube = 150 cm²
Side = \( \sqrt { \frac { 150 }{ 6 } } \)
= √25
= 5 cm
Volume = (side)³
= (5)³
= 125 cm³ (b)

Question 3.
Solution:
Volume of cube = 343 cm²
Side = \( \sqrt [ 3 ]{ 343 } =\sqrt [ 3 ]{ 7\times 7\times 7 } \)
= 7 cm
Total surface area = 6 (side)²
= 6 x (7)²
= 6 x 49 cm²
= 294 cm² (c)

Question 4.
Solution:
Rate of painting = 10 paise per cm²
Total cost = Rs. 264.60
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 4.1

Question 5.
Solution:
Answer = (c)
Length of wall (l) = 8m = 800 cm
Breadth (b) = 22.5 cm
Height (h) = 6 m
= 600 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 5.1

Question 6.
Solution:
Answer = (c)
Edge of cube = 10 cm
Volume = a³ = (10)³ = 1000 cm³
Edge of box = 1 m = 100 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 6.1

Question 7.
Solution:
Answer = (a)
Ratio in sides of a cuboid = 1 : 2 : 3
Surface area = 88 cm²
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 7.1

Question 8.
Solution:
Ratio in the two volumes = 1 : 27
Let volume of first volume = x³
and volume of second volume = 27x³
Side of first cube = x
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 8.1

Question 9.
Solution:
Surface area of a brick of measure 10 cm x 4 cm x 3 cm
= 2 (l x b + b x h + h x l)
= 2 [10 x 4 + 4 x 3 + 3 x 10] cm²
= 2 [40 + 12 + 30]
= 82 x 2
= 164 cm² (c)

Question 10.
Solution:
Length of beam (l) = 9 m
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 10.1

Question 11.
Solution:
Water in rectangular reservoir = 42000
Volume = \(\\ \frac { 42000 }{ 1000 } \) = 42 m³
Length (l) = 6 m
Breadth (b) = 3.5 m
Depth = \(\\ \frac { volume }{ l\times b } \)
= \(\\ \frac { 42 }{ 6\times 3.5 } \)
= 2 m (c)

Question 12.
Solution:
Dimensions of a room are 10 m, 8 m, 3.3 m
Volume of air in it = lbh
= 10 x 8 x 3.3 = 264 m³
Air required for one man = 3 m³
No. of men = \(\\ \frac { 264 }{ 3 } \)
= 88 (b)

Question 13.
Solution:
Length of water tank (l) = 3 m
Width (b) = 2 m
and height (h) = 5 m
Volume = lbh = 3 x 2 x 5 = 30 m³
Water in it = 30 x 1000
= 30000 (a)

Question 14.
Solution:
Size of box = 25 cm, 15 cm, 8 cm
Surface area = (lb + bh + hl)
= 2 ( 25 x 15 + 15 x 8 + 8 x 25) cm²
= 2 (375 + 120 + 200) cm²
= 2(695)
= 1390 cm²(b)

Question 15.
Solution:
Diagonal of cube = 4√3
Side = \( \frac { 4\sqrt { 3 } }{ \sqrt { 3 } } \)
= 4 cm
Volume = a³ = (4)³
= 64 cm³ (d)

Question 16.
Solution:
Diagonal of cube = 9√3 cm
Side = \( \frac { 9\sqrt { 3 } }{ \sqrt { 3 } } \)
= 9 cm
Surface area = 6a²
= 6 (9)² = 6 x 81 cm²
= 486 cm² (b)

Question 17.
Solution:
Let side of cube in first case = a
Then volume = a³
If side of cube is doubled, then side = 2a
Volume (2a)³ = 8a³
Becomes 8 times (d)

Question 18.
Solution:
Let side of cube in first case = a
Then surface area = 6a²
and side of second cube = 2a
Surface area = 6 (2a)² = 6 x 4a² = 24a²
Ratio = \(\frac { { 24a }^{ 2 } }{ { 6a }^{ 2 } } \) = 4
Becomes 4 times (b)

Question 19.
Solution:
Sides (edges) of 3 cubes are 6 cm, 8 cm, and 10 cm respectively
Volume of first cube = (6)³ = 216 cm³
Volume of second cube = (8)³ = 512 cm³
and volume of third cube
= (10)³ = 1000 cm³
Sum of volumes of 3 cubes = 216 + 512 + 1000
= 1728 cm³
Volume of new single cube = 1728 cm³
Edge = \(\sqrt [ 3 ]{ 1728 } \)
\(\sqrt [ 3 ]{ { \left( 12 \right) }^{ 3 } } \)
= 12 cm (a)

Question 20.
Solution:
Each edge of 5 cubes = 5 cm
Placing than adjacent to each other
Length of new cuboid (l)
= 5 x 5 = 25 cm
Breadth (b) = 5 cm
and height (h) = 5 cm
Volume of new cuboid = lbh
= 25 x 5 x 5 cm³
= 625 cm³ (d)

Question 21.
Solution:
Diameter of circular well = 2n
Radius = \(\\ \frac { 2 }{ 2 } \) = 1 m
Depth(h) = 14 m
Volume of earth dug out = πr²h
= \(\\ \frac { 22 }{ 7 } \) x 1 x 1 x 14
= 44 m (d)

Question 22.
Solution:
Capacity of cylindrical tank = 1848 m³
Diameter = 14 m
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 22.1

Question 23.
Solution:
Radius of a cylinder (r) = 20 cm
and height (h) = 60 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 23.1

Question 24.
Solution:
Radius of each coin (r) = 0.75 cm
and thickness (h) = 0.2 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 24.1

Question 25.
Solution:
Volume of silver = 66 cm³
Diameter of wire = 1 mm = \(\\ \frac { 1 }{ 10 } \)
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 25.1

Question 26.
Solution:
Diameter of cylinder = 10 cm
Radius (r) = \(\\ \frac { 10 }{ 2 } \) = 5 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 26.1

Question 27.
Solution:
Diameter of cylinder = 7 cm
Radius (r) = \(\\ \frac { 7 }{ 2 } \) cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 27.1

Question 28.
Solution:
Curved surface area of a cylinder = 264 cm³
Height (h) = 14 cm
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 28.1

Question 29.
Solution:
Diameter of cylinder = 14 cm
Radius (r) = 7 cm
Curved surface area = 220 cm²
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 29.1

Question 30.
Solution:
Ratio in radii of two cylinder = 2 : 3
and ratio in their height = 5 : 3
Let radii of two cylinder = 2x and 3x
and corresponding heights = 5y, 3y
RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C 30.1

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

January 5, 2022July 6, 2018 by Prasanna

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

Other Exercises

Question 1.
Find the surface area of a sphere of radius.
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
Solution:
In a sphere,
(i) Radius (r) = 10.5 cm
Surface area = 4πr²
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 1.1

Question 2.
Find the surface area of a sphere of diameter
(i) 14 cm
(ii) 21 cm
(iii) 3.5 cm
Solution:
(i) Diameter of a sphere = 14 cm
Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 2.1

Question 3.
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm. [Use π = 3.14]
Solution:
(i) Radius of hemisphere = 10 cm
∴ Total surface area of hemisphere = 2πr²
= 2 x 3.14 x 10 x 10 cm²
= 628 cm²
(ii) Total surface area of solid hemisphere
= 3πr² = 3 x 3.14 x 10 x 10 cm²
= 942 cm²

Question 4.
The surface area of a sphere in 5544 cm², find the diameter.
Solution:
Let r be the radius of a sphere, then Surface area = 4πr²
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 4.1

Question 5.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹4 per 100 cm². [NCERT]
Solution:
Inner diameter of a hemispherical bowl = 10.5 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 5.1

Question 6.
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of painting it at the rate of ₹2 per sq. m.
Solution:
Radius of dome (hemispherical) = 63 dm
Area of curved surface
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 6.1

Question 7.
Assuming the earth to be a sphere of radius 6370 km, how many square kilometres is area of the land, if three-fourth of the earth’s surface is covered by water?
Solution:
Radius of earth (sphere) = 6370 km
Water on the earth = \(\frac { 3 }{ 4 }\) % total area
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 7.1

Question 8.
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved surface area of the shape if the length of the shape be 7 cm.
Solution:
Total height of the so formed shape = 7 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 8.1

Question 9.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution:
Diameter of moon = \(\frac { 1 }{ 4 }\) of diameter of earth
Let radius of earth = r km
Then radius of moon = \(\frac { 1 }{ 4 }\) r km
Now surface area of earth = 4πr²
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 9.1

Question 10.
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is ₹5 per 100 cm². [NCERT]
Solution:
Circumference of the base of dome (r) = 17.6 m
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 10.1

Question 11.
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at ₹7 per 100 cm².
Solution:
Diameter of toy = 16 cm
Radius (r) = \(\frac { 16 }{ 2 }\) = 8 cm
Height of conical part (h) = 15 cm
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 11.1

Question 12.
A storage tank consists of a circular cylinder with a hemisphere adjoined on either end. If the external diameter of the cylinder be 1.4 m and its length be 8 m, find the cost of painting it on the outside at the rate of ₹10 per m².
Solution:
Diameter of the tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) m = 0.7 m
and height of cylindrical portion = 8m
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 12.1

Question 13.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the figure. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm². [NCERT]
RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 13.1
Solution:
Diameter of each spheres = 21 cm
∴ Radius (R) = \(\frac { 21 }{ 2 }\) cm
Radius of each cylinder (r) = 1.5 cm
and height (h) = 7 cm

Now surface area of one sphere = 4πR²