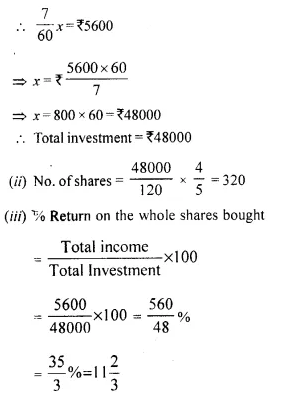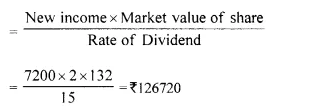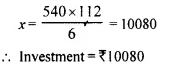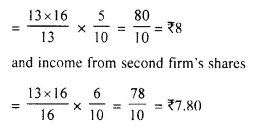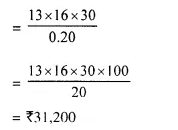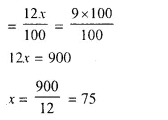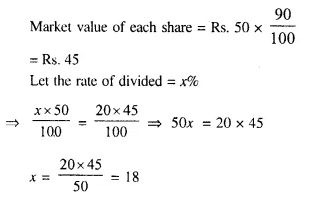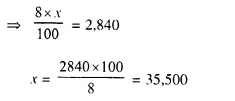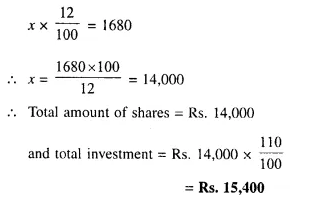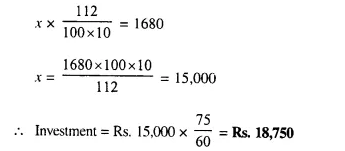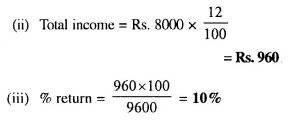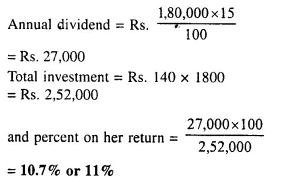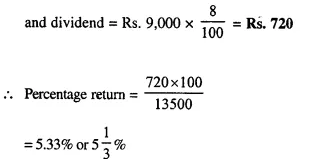Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3C
Question 1.
How much money will be required to buy 400, ₹ 12.50 shares at a premium of ₹ 1?
Solution:
Number of shares purchased = 400
Rate of each share = ₹ 12.50
M.V. = ₹ 1 premium = ₹ 12.50 + ₹ 1 = ₹ 13.50
Amount of in vestment = ₹ 400 x ₹ 13.50 = ₹ 5400
Question 2.
How much money will be required to buy 250, ₹ 15 shares at a discount of ₹ 1.50?
Solution:
Number of shares = 250
M.V. = at ₹ 15 at a discount of ₹ 1.50 = ₹ 15 – ₹ 1.50 = ₹ 13.50
Amount of investment = ₹ 13.50 x 250 = ₹ 3375
Question 3.
A person buys 120 shares at a nominal value of ₹ 40 each, which he sells at ₹ 42.50 each. Find his profit and profit percent.
Solution:
No. of shares = 120
Nominal value of each share = ₹ 40.00
Profit at each share = ₹ 42.50 – ₹ 40.00 = ₹ 2.50
Total profit = 2.50 x 120 = ₹ 300
Cost price of 120 shares = ₹ 40 x 120 = ₹ 4,800
Question 4.
Find the cost of 85 shares of Rs. 60 each when quoted at ₹ 63.25
Solution:
No. of shares = 85
Market value of cach share = ₹ 63.25
Total cost = ₹ 63.25 x 85 = ₹ 5,376.25
Question 5.
A man invests ₹ 800 in buying 75 shares and when they are selling at a premium of ₹ 1.15, he sells all the shares. Find his profit and profit percent.
Solution:
Investment = ₹ 800
In first case face value of each share = ₹ 5
and market value of each share = ₹ 5.00 + ₹ 1.15 = ₹ 6.15
Gain on each share of ₹ 5 = ₹ 1.15
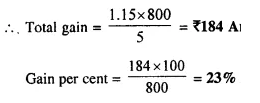
Question 6.
Find the annual income derived from 125, ₹ 120 shares paying 5% dividend.
Solution:
Amount of investment = ?
Number of shares purchased = 125 at ₹ 120, 5% dividend
Amount of investment = ₹ 125 x 120 = ₹ 15000
His annual income = 15000 x \(\frac { 5 }{ 100 }\) = ₹ 750
Question 7.
A man invests ₹ 3,072 in a company paying 5% per annum when its ₹ 10 share can be bought for ₹ 16 each. Find:
(i) his annual income;
(ii) his percentage income on his investment.
Solution:
Total investment = ₹ 3,072
Market value of each shares = ₹ 16
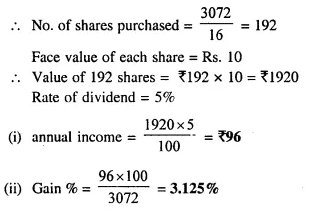
Question 8.
A man invests ₹ 7,770 in a company paying 5 percent dividend when a share of nominal value of ₹ 100 sells at a premium of ₹ 5. Find :
(i) the number of shares bought;
(ii) annual income ;
(iii) percentage income ;
Solution:
Investment = ₹ 7770
Nominal value of each share = 100
Market value = 100 + 5 = 105
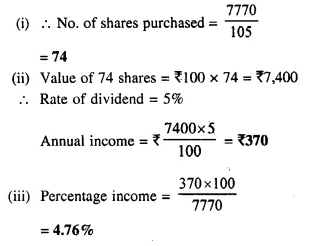
Question 9.
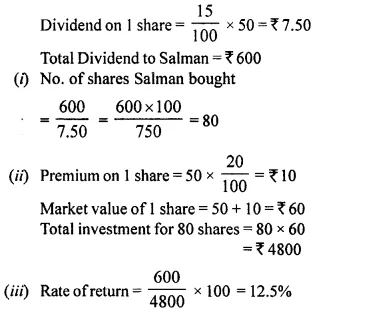
A man buys ₹ 50 shares of a company paying 12 percent dividend, at a premium of ₹ 10. Find :
(i) the market value of 320 shares ;
(ii) his annual income ;
(iii) his profit percent.
Solution:
(i) Market value of each share = ₹ 50 + ₹ 10 = ₹ 60
Market value of 320 shares = ₹ 60 x 320 = ₹ 19,200
(ii) Rate of dividend = 12%
Face value of 320 shares = Rs. 50 x 320 = Rs. 16,000
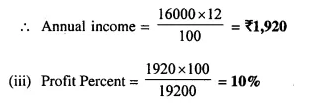
Question 10.
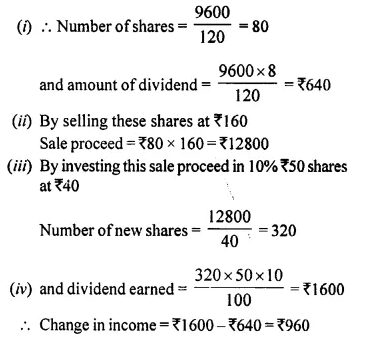
A man buys of Rs. 75 shares at a discount of Rs. 15 of a company paying 20% dividend. Find :
(i) the market value of 120 shares ;
(ii) his annual income ;
(iii) his profit percent.
Solution:
(i) Market value of one share = Rs. 75 – 15 = Rs. 60
Market value of 120 shares = Rs. 60 x 120 = Rs. 7,200
(ii) Rate of dividend = 20%
Face value of 120 shares = Rs. 75 x 120 = Rs. 9,000
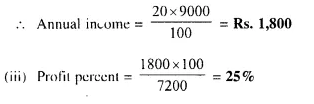
Question 11.
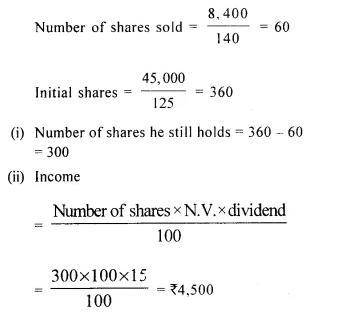
A man has 300, ₹ 50 shares of a company paying 20% dividend. Find his net income after paying 3% income tax.
Solution:
No. of shares = 300
Face value of 50 shares = Rs. 50 x 300 = Rs. 15,000
Rate of dividend = 20%

Question 12.
A company pays dividend of 15 % on its ten-rupee shares from which it deducts income tax at the rate of 22%. Find the annual income of a man who owns one thousand shares of this company.
Solution:
No. of shares = 1,000
Face Value of each share = Rs. 10
Rate of dividend = 15%
Rate of income tax = 22%
Face value of 1,000 shares = 1,000 x 10 = Rs. 10,000
Total dividend = Rs. 10,000 x \(\frac { 15 }{ 100 }\) = Rs. 1,500
Income tax deducted = Rs. 1500 x \(\frac { 22 }{ 100 }\) = Rs. 330
Net income = Rs.1500 – Rs. 330 = Rs. 1170
Question 13.
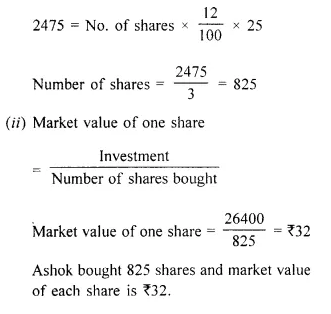
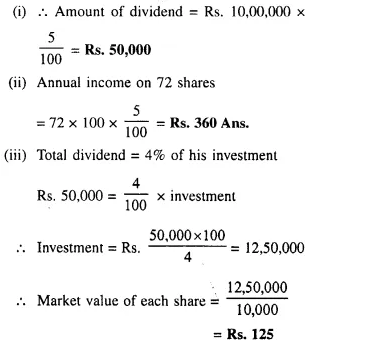
A man invests Rs. 8,800 in buying shares of a company of face value of rupees hundred each at a premium of 10%. If he earns Rs. 1,200 at the end of the year as dividend find:
(i) the number of shares he has in the company;
(ii) the dividend percent per share. [2001]
Solution:
Investment = Rs. 8,800
Face value of each share = Rs. 100
Market value of each share = Rs. 100 + 10 = Rs. 110

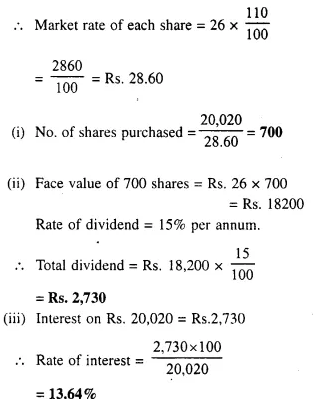
Question 14.
A man invests Rs. 1,680 in buying shares of nominal value Rs. 24 and selling at 12% premium. The dividend on the shares is 15% per annum. Calculate :
(i) The number of shares he buys ;
(ii) The dividend he receives annually. [1999]
Solution:
Investment = Rs. 1680
Nominal value of each share = Rs. 24
Market value of each share = Rs. 24 + 12% of 24
= Rs. 24 + 2.88 = Rs. 26.88
Rate of dividend = 15%
(i) No. of shares = \(\frac { 1680 }{ 26.88 }\) = 62.5
(ii) Face value of 62.5 shares = 62.5 x 24 = Rs. 1500
Amount of dividend = 1500 x \(\frac { 15 }{ 100 }\) = Rs. 225
Question 15.
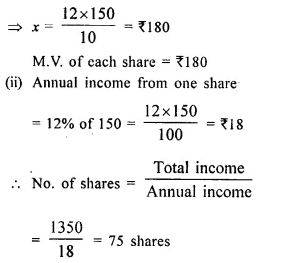
By investing Rs. 7,500 in a company paying 10 percent dividend, an annual income of Rs. 500 is received. What price is paid for each of Rs. 100 share? [1990]
Solution:
Investment = Rs. 7,500
Rate of dividend = 10%
Total income = Rs. 500
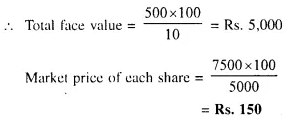
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 3 Shares and Dividend Ex 3A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.