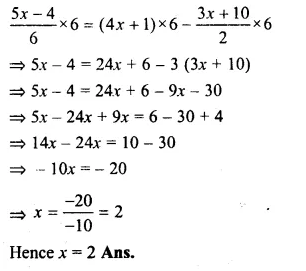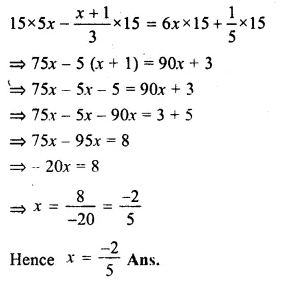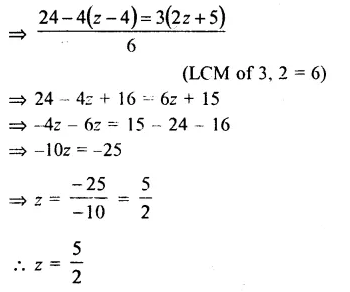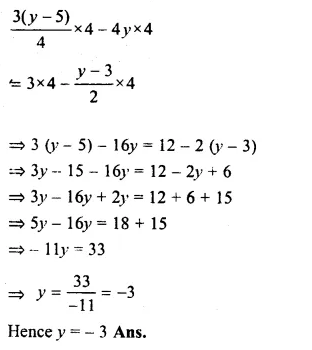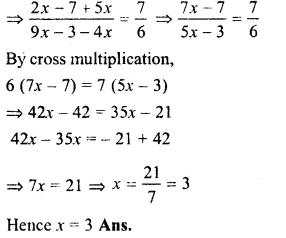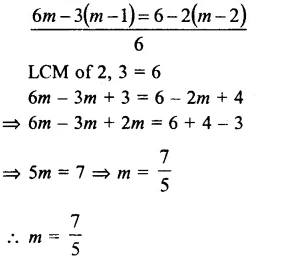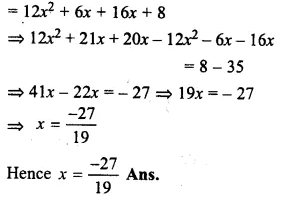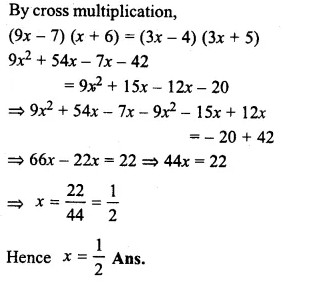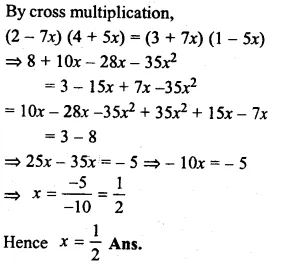RS Aggarwal Class 8 Solutions Chapter 8 Linear Equations Ex 8C
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8C.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8A
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8B
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8C
Objective Questions :
Tick the correct answer in each of the following:
Question 1.
Solution:
2x – 3 = x + 2
=> 2x – x
= 2 + 3
= 5 (c)
Question 2.
Solution:
5x + \(\\ \frac { 7 }{ 2 } \) = \(\\ \frac { 3 }{ 2 } \) x – 14
=> 5x – \(\\ \frac { 3 }{ 2 } \) x = – 14 – \(\\ \frac { 7 }{ 2 } \)
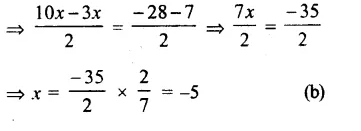
Question 3.
Solution:
z = \(\\ \frac { 4 }{ 5 } \)(z + 10)
=> 5z = 4z + 40
=> 5z – 4z = 40
=> z = 40 (a)
Question 4.
Solution:
3m = 5m – \(\\ \frac { 8 }{ 5 } \)
=> 3m – 5m = \(\\ \frac { -8 }{ 5 } \)
=> – 2m = \(\\ \frac { -8 }{ 5 } \)
=> m = \(\\ \frac { -8 }{ -5×2 } \) = \(\\ \frac { 4 }{ 5 } \) (c)
Question 5.
Solution:
5t – 3 = 3t, – 5
=> 5t – 3t = – 5 + 3
=> 2t = – 2
=> t = \(\\ \frac { -2 }{ 2 } \) = – 1 (b)
Question 6.
Solution:
2y + \(\\ \frac { 5 }{ 3 } \) = \(\\ \frac { 26 }{ 3 } \) – y
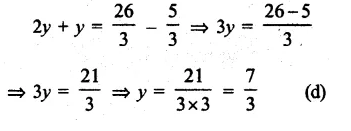
Question 7.
Solution:
\(\\ \frac { 6x+1 }{ 3 } \) +1 = \(\\ \frac { x-3 }{ 6 } \)
\(\\ \frac { 12x+2+6=x-3 }{ 6 } \)
12x – x = – 3 – 2 – 6
11x – 11
=> x = \(\\ \frac { -11 }{ 11 } \) = – 1 (b)
Question 8.
Solution:
\(\\ \frac { n }{ 2 } \) – \(\\ \frac { 3n }{ 4 } \) + \(\\ \frac { 5n }{ 6 } \) = 21
\(\\ \frac { 6n-9n+10n= 252 }{ 12 } \)
LCM of 2, 4, 6 = 12
16n – 9n = 252
=> 7n = 252
=> n = \(\\ \frac { 252 }{ 7 } \) = 36 (c)
Question 9.
Solution:
\(\\ \frac { x+1 }{ 2x+3 } \) = \(\\ \frac { 3 }{ 8 } \)
=> 8 (x + 1) = 3 (2x + 3)
(By cross multiplication)
x + 8x + 9 = 8x – 6x = 9 – 8
=> 2x = 1
=> x = \(\\ \frac { 1 }{ 2 } \)
x = \(\\ \frac { 1 }{ 2 } \) (d)
Question 10.
Solution:
\(\\ \frac { 4x+8 }{ 5x+8 } \) = \(\\ \frac { 5 }{ 6 } \)
6(4x + 8) = 5(5x + 8)
(By cross multiplication)
24x + 48 = 25x + 40
=> 24x – 25x = 40 – 48
=> – x = – 8
=> x = 8 (c)
Question 11.
Solution:
\(\\ \frac { n }{ n+15 } \) = \(\\ \frac { 4 }{ 9 } \)
9n = 4n + 60
(By cross multiplication)
9n – 4n = 60
=> 5n = 60
=> n = \(\\ \frac { 60 }{ 5 } \) = 12
n = 12 (d)
Question 12.
Solution:
3(t – 3) = 5 (2t + 1)
3t – 9 = 10t + 5
=> 3t – 10t = 5 + 9
=> – 7t = 14
=> t = \(\\ \frac { 14 }{ -7 } \) = – 2
t = – 2 (a)
Question 13.
Solution:
Let number = x
Then \(\\ \frac { 4 }{ 5 } \)x = \(\\ \frac { 3 }{ 4 } \)x + 4
=> \(\\ \frac { 16x=15x+80 }{ 20 } \)
16x – 15x = 80
=> x = 80
:. Number = 80 (c)
Question 14.
Solution:
Ages of A : B = 5 : 7
Let A’s age = 5x
Then B’s age = 7x
After 4 years
A’s age = 5x + 4
and B’s age = 7x + 4
\(\\ \frac { 5x+4 }{ 7x+5 } \) = \(\\ \frac { 3 }{ 4 } \)
=> 3(7x + 4) = 4(5x + 4)
21x + 12 = 20x + 16
=>21x – 20x = 16 – 12
x = 4
B’s age = 7x
= 7 x 4
= 28 years (b)
Question 15.
Solution:
Perimeter of an isosceles triangle = 16 cm
and base = 6 cm
Let each equal side = x cm
x + x + 6 = 16
=> 2x = 16 – 6 = 10
=> x = \(\\ \frac { 10 }{ 2 } \) = 5
Each equal side = 5 cm (b)
Question 16.
Solution:
Let first number = x
Then second number = x + 1
and third number = x+ 2
x + x + 1 + x + 2 = 51
=> 3x + 3 = 51
=> 3x = 51 – 3 = 48
=> x = \(\\ \frac { 48 }{ 3 } \) = 16
Middle number = x + 1 = 16 + 1 = 17 (b)
Question 17.
Solution:
Let first number = x
Then second number = x + 15
x + x + 15 = 95
=> 2x = 95 – 15 = 80
=> x= \(\\ \frac { 80 }{ 2 } \) = 40
=> Smaller number = 40
Question 18.
Solution:
Ratio in boys and girls in a class = 7:5
Let no. of boys = 7x
Then no. of girls = 5x
7x – 5x = 8
=> 2x = 8
x = \(\\ \frac { 8 }{ 2 } \) = 4
Total strength = 7x + 5x = 12x
= 12 x 4
= 48 (c)
Hope given RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.