RS Aggarwal Class 8 Solutions Chapter 8 Linear Equations Ex 8B
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8B.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8A
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8B
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8C
Question 1.
Solution:
The numbers be 8x and 3x (∵ Ratio is 8 : 3)
Sum = 143
According to the condition
8x + 3x = 143
=> 11x = 143
=> x = \(\\ \frac { 143 }{ 11 } \) = 13
First number = 8x = 8 x 13 = 104
and second number = 3x = 3 x 13 = 39 Ans.
Question 2.
Solution:
Let the number = x
According to the condition,
x – \(\frac { 2 }{ 3 } x\) = 20
=> \(\\ \frac { 3x-2x }{ 3 } \) = 20
=> \(\\ \frac { x }{ 3 } \) = 20
=> x = 20 x 3 = 60
Hence original number = 60 Ans.
You can also Download NCERT Solutions for Class 8 Maths to help you to revise complete Syllabus and score more marks in your examinations.
Question 3.
Solution:
Let the number = x
According to the condition
\(\frac { 4 }{ 5 } x-\frac { 2 }{ 3 } x\) = 10
=> \(\\ \frac { 12x-10x }{ 15 } \) = 10
=> \(\\ \frac { 2x }{ 15 } \) = 10
=> 2x = 10 x 15
x = \(\\ \frac { 10 x 15 }{ 2 } \) = 75
Hence number = 75 Ans.
Question 4.
Solution:
Let first part = x
then second part = 24 – x (∵ Sum = 24)
According to the condition,
7x + 5 (24 – x) = 146
=> 7x + 120 – 5x = 146
=> 2x = 146 – 120 = 26
=> x = \(\\ \frac { 26 }{ 2 } \) = 13
First part = 13
and second part = 24 – 13 = 11 Ans.
Question 5.
Solution:
Let number = x
According to the condition
\(\frac { x }{ 5 } +5=\frac { x }{ 4 } -5\)
=> \(\\ \frac { x }{ 5 } \) – \(\\ \frac { x }{ 4 } \)= – 5 – 5
=> \(\\ \frac { 4x-5x }{ 20 } \) = – 10
=> \(\\ \frac { -x }{ 20 } \) = – 10 = \(\\ \frac { x }{ 20 } \) = 10
=> x = 10 × 20 = 200
Hence number = 200 Ans.
Question 6.
Solution:
Ratio between three numbers = 4:5:6
Let the largest number = 6x
smallest number = 4x
and third number = 5x
According to the condition,
6x + 4x = 5x + 55
=> 10x = 5x + 55
=> 10x – 5x = 55
=> 5x = 55
=> x = \(\\ \frac { 55 }{ 5 } \) = 11
Numbers will be 4x = 4 × 11 = 44,
5x = 5 × 31 = 55 and 6x = 6 × 11 = 66
Hence numbers are 44, 55, 66 Ans.
Question 7.
Solution:
Let the number = x
According to the condition,
4x + 10 = 5x – 5
=> 4x – 5x = – 5 – 10
=> – x = – 15
x = 15
Hence number = 15 Ans.
Question 8.
Solution:
Ratio between two numbers 3: 5
Let first number = 3x
and second number = 5x
Now according to the condition.
3x + 10 : 5x + 10 = 5 : 7

Question 9.
Solution:
Let first odd number = 2x + 1
second number 2x + 3
and third number = 2 + 5
According to the condition.
2x + 1 + 2x + 3 + 2x + 5 = 147
=> 6x + 9 = 147
=> 6x = 147 – 9 = 138
=> x = \(\\ \frac { 138 }{ 6 } \) = 23
Hence first odd number 2x + 1
= 23 x 2 + 1 = 46 + 1 = 47
Second number 47 + 2 = 49
and third number = 49 + 2 = 51 Ans.
Question 10.
Solution:
Let first even number = 2x
second number = 2x + 2
and third number = 2x + 4
According to the condition,
2x + 2x + 2 + 2x + 4 = 234
=> 6x + 6 = 234
=> 6x = 234 – 6
=> 6x = 228
=> x = \(\\ \frac { 228 }{ 6 } \) = 38
First even number = 2x = 38 x 2 = 76
second number = 76 + 2 = 78
and third number 78 + 2 = 80 Ans.
Question 11.
Solution:
The sum of two digits = 12
Let the ones digit of the number = x
then tens digit = 12 – x
and number = x + 10 (12 – x)
= x + 120 – 10x = 120 – 9x
Reversing the digits,
ones digit of new number = 12 – x
and tens digit = x
the number = 12 – x + 10x = 12 + 9x
According to the condition,
12 + 9x = 120 – 9x + 54
=> 9x + 9x
=> 120 + 54 – 12
=> 174 – 12
=> 18x = 162
=> x = \(\\ \frac { 162 }{ 18 } \) = 9
Original number = 120 – 9x
= 120 – 9 x 9
= 120 – 81
= 39
Hence number 39 Ans.
Check :Original number= 39
Sum of digits = 3 + 9 = 12
Now reversing its digit the new number
will be = 93
and 93 – 39 = 54 which is given.
Question 12.
Solution:
Let units digit of the number = x
then tens digit = 3x
and number = x + 10
3x = x + 30x = 31x
on reversing the digits.
units digit = 3x
and tens digit = x
then number 3x + 10x = 13x
According to the condition,
31x – 36 = 13x
=> 31x – 13x = 36
=> 18 x 36
=> x = \(\\ \frac { 36 }{ 18 } \) = 2
The original number = 31x = 31 x 2 = 62
Hence number = 62 Ans.
Check : Number = 62
tens digit = 2 x 3 = 6
On reversing the digit, the new number will be = 26
62 – 26 = 36 which is given.
Question 13.
Solution:
Let numerator of a rational number = x
Then its denominator = x + 7

Question 14.
Solution:
Let numerator of a fraction = x
The denominator = 2x – 2
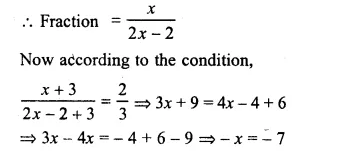
Question 15.
Solution:
Let breadth of the rectangle = x cm
then length = x + 7
Area = l × b = (x + 7) × x
In second case,
Length of the new rectangle = x + 7 – 4
= x + 3 cm
and breadth = x + 3
Area = (x + 3)(x + 3)
According to the condition,
(x + 3)(x + 3) = x(x + 7)
x2 + 3x + 3x + 9 = x2 + 7x
=> x2 + 6x – 7x – x2 = – 9
=> x = – 9
=> x = 9
Length of the original rectangle
= > x + 7 = 9 + 7 = 16 cm
and breadth = x = 9 cm. Ans.
Question 16.
Solution:
Let length of rectangle = x m
then width = \(\frac { 2 }{ 3 } x\)m
Perimeter = 2 (l + b) m
=> \(2\left( x+\frac { 2 }{ 3 } x \right) =180\)
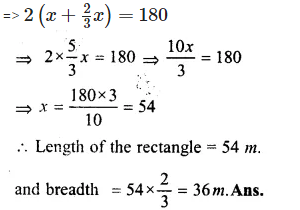
Question 17.
Solution:
Let the length of the base of the triangle = x cm
then altitude = \(\frac { 5 }{ 3 } x\)cm
Area = \(\\ \frac { 1 }{ 2 } \) base x altitude

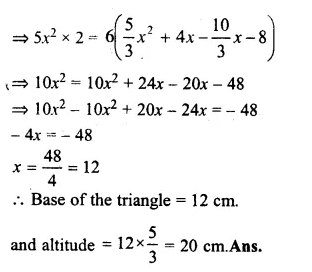
Question 18.
Solution:
Let ∠A, ∠B and ∠C are the three angles of a triangle and
Let ∠A + ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
∠C + ∠C = 180°
=> 2∠C = 180°
∠C = 90°
and ∠A + ∠B = 90°
Let ∠A = 4x and ∠B = 5x
4x + 5x = 90°
=> 9x = 90°
x = \(\frac { { 90 }^{ o } }{ 9 } \) = 10°
∠A = 4x = 4 x 10° = 40°
and ∠B = 5x = 5 x 10° = 50°
and ∠C = 90° Ans.
Question 19.
Solution:
Time taken downstream = 9 hour
and time taken upstream = 10 hour
Speed of stream = 1 km/h
Let the speed of a steamer in still water
= x km/h.
Distance downstream = 9(x + 1) km.
and upstream = 10 (x – 1) km.
According to the condition,
10(x – 1) = 9(x + 1)
l0x – 10 = 9x + 9
=> 10x – 9x = 9 + 10
=> x = 19
Hence speed of steamer in still water = 19 km/h
and distance = 9(x + 1)
= 9(19 + 1)
= 9 x 20km
= 180km. Ans.
Question 20.
Solution:
The distance between two stations = 300 km
Let the speed of first motorcyclists = x km/h
and speed of second motorcyclists = (x + 7)km/h
Distance covered by the first = 2x km
and distance covered by the second = 2 (x + 7) km
= 2x + 14 km
Distance uncovered by them = 300 – (2x + 2x + 14)kms.
According to the condition,
300 – (4x + 4) = 34
=> 300 – 4x – 14 = 34
=> 300 – 14 – 34 = 4x
=> 4x = 300 – 48
=> 4x = 252
=> x = \(\\ \frac { 252 }{ 4 } \) = 63
Speed of the first motorcyclists = 63km/h
and speed of second = 63 + 7 = 70 km/h
Check. Distance covered by both of them
= 2 x 63 + 2 x 70 = 126 + 140 = 266
Total distance = 300 km.
Distance between them = 300 – 266 = 34 km.
which is given.
Question 21.
Solution:
Sum of three numbers = 150
Let first number = x
then second number = \(\frac { 5 }{ 6 } x\)
and third number = \(\\ \frac { 4 }{ 5 } \) of second

Question 22.
Solution:
Sum of two pans = 4500
Let first part = x
then second part = 4500 – x
According to the condition,
5% of x = 10% of (4500 – x)
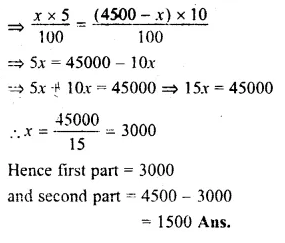
Question 23.
Solution:
Let age of Rakhi = x years
then her mother’s age = 4x
After 5 years,
Rakhi’s age = x + 5
and her mother’s age = 4x + 5
According to the conditions,
4x + 5 = 3 (x + 5)
=> 4x + 5 = 3x + 15
=> 4x – 3x = 15 – 5
=> x = 10
Rakhi ‘s present age = 10 years
and her mother’s age = 4 x 10
= 40 years Ans.
Question 24.
Solution:
Let age of Monu = x year
His father’s age = x + 29
and his grandfather’s age = x + 29 + 26
= x + 55
and sum of their ages = 135 years
Now,
x + x + 29 + x + 55 = 135
=> 3x + 84 = 135
=> 3x = 135 – 84 = 51
=> x = \(\\ \frac { 51 }{ 3 } \) = 17 years
Monu’s age = 17 years
His father age = 17 + 29 = 46 years
and his grandfather’s age = 46 + 26 = 72 years
Question 25.
Solution:
Let age of grandson = x year
Then his age = 10x
But 10x = x + 54
=> 10x – x = 54
=> 9x = 54
=> x = \(\\ \frac { 54 }{ 9 } \) = 6
Grand’s son age = 6 years
and his age = 6 x 10 = 60 years
Question 26.
Solution:
Let age of elder cousin = x years
and age of younger = (x – 10) years.
15 years ago,
age of older, cousin = x – 15 years
and age of younger = x – 10 – 15
= (x – 25) years.
According to the condition,
x – 15 = 2(x – 25)
=> x – 15 = 2x – 50
=> 2x – x = 50 – 15
=> x = 35
Age of elder cousin = 35 years
and age of younger = 35 – 10
= 25 years Ans.
Question 27.
Solution:
Let number of deer = x
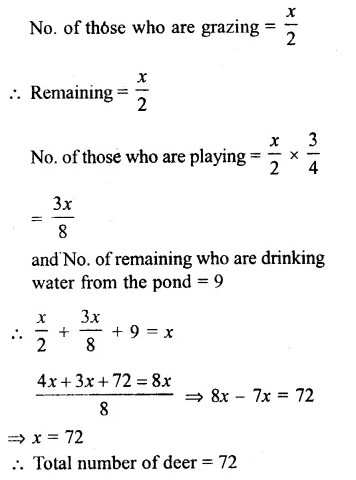
Hope given RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.