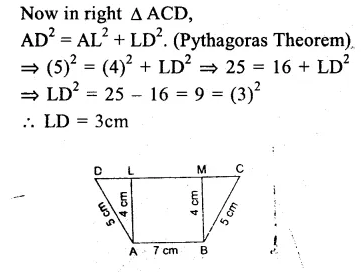
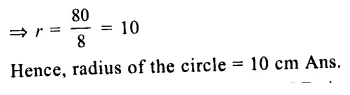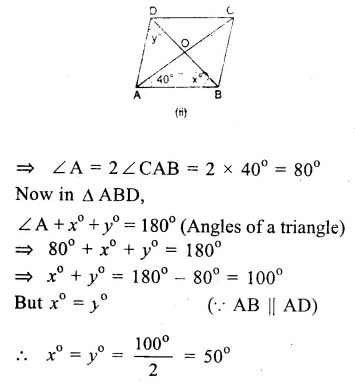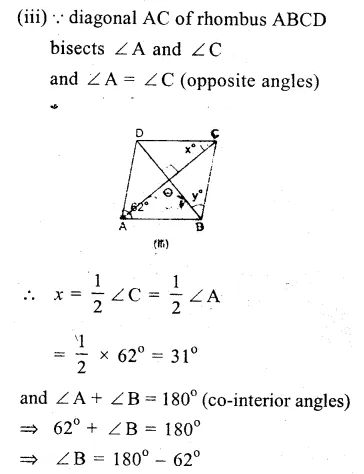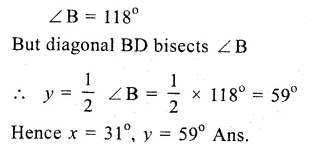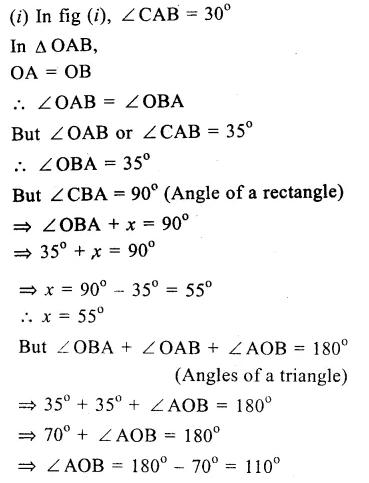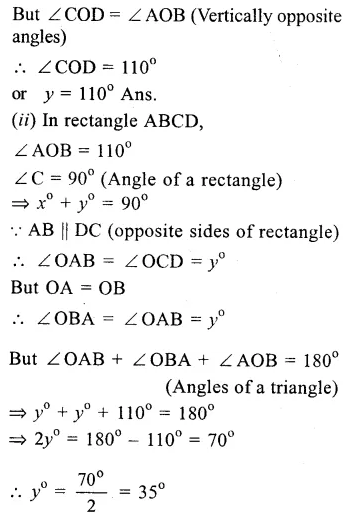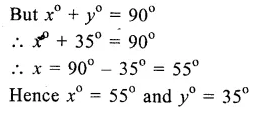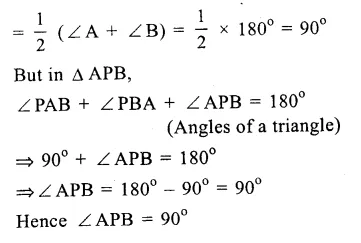RS Aggarwal Class 9 Maths Solutions

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C

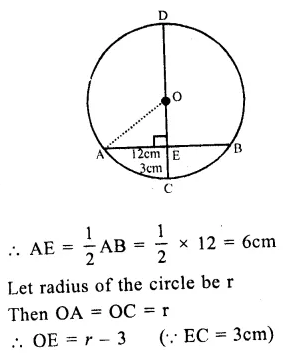
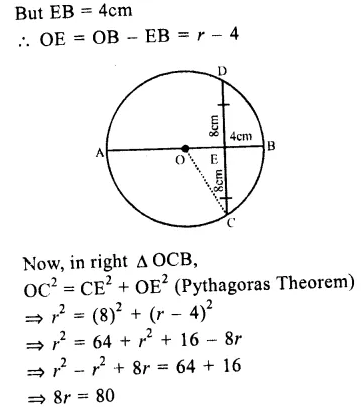
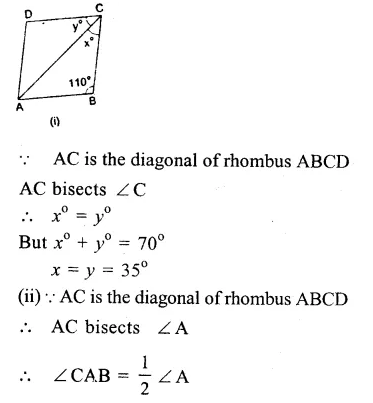
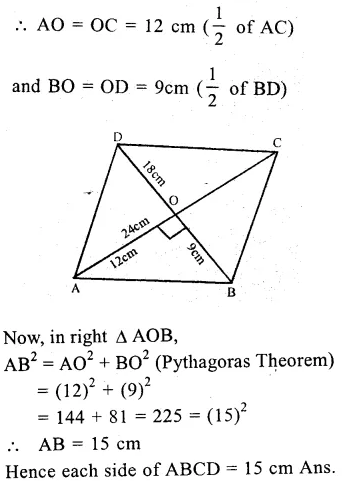
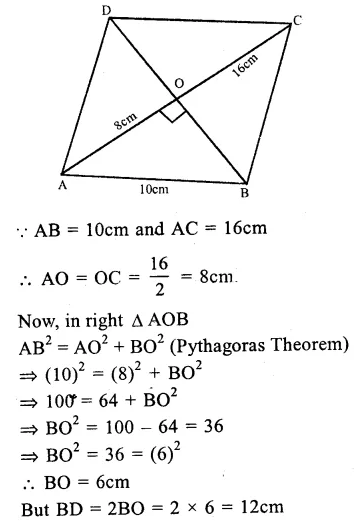
Question 1.
Solution:
(i) O is the centre of the circle
∠OAB = 40°, ∠OCB = 30°
Join OB.

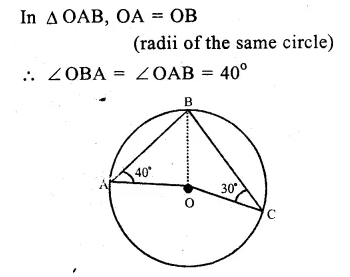
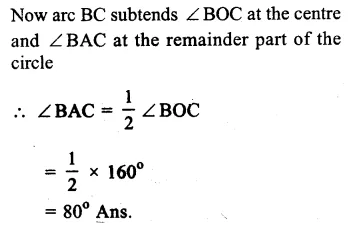
Question 2.
Solution:
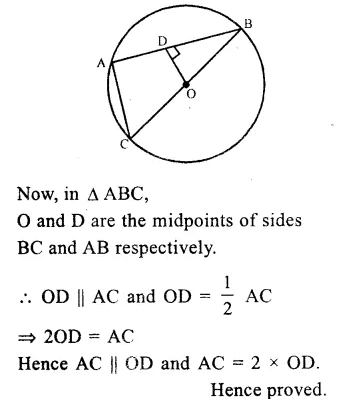
O is the centre of the cirlce and ∠AOB = 70°
∵ Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∵ ∠ACB = \(\frac { 1 }{ 2 } \) ∠AOB = \(\frac { 1 }{ 2 } \) x 70°
=> ∠ACB = 35°
or ∠OCA = 35°
In ∆OAC,
OA = OC (radii of the same circle)
∴ ∠OAC = ∠OCA = 35° Ans.

Question 3.
Solution:
In the figure, O is the centre of the circle. ∠PBC = 25°, ∠APB =110°
∠ APB + ∠ BPC = 180° (Linear pair)
=> 110° + ∠ BPC = 180°

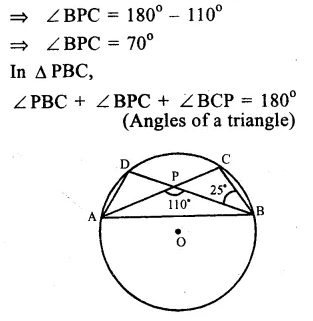
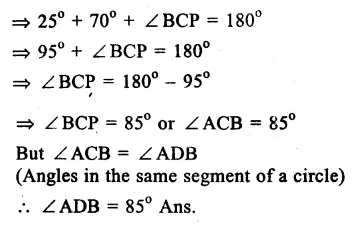
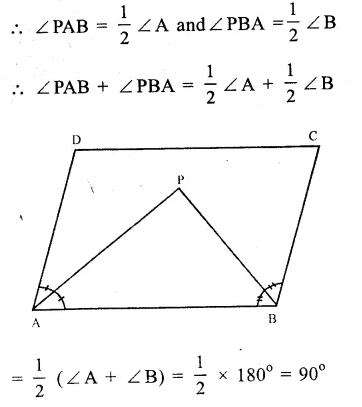
Question 4.
Solution:
O is the centre of the circle
∠ABD = 35° and ∠B AC = 70°
BOD is the diameter of the circle
∠BAD = 90° (Angle in a semi circle)
But ∠ADB + ∠ABD + ∠BAD = 180° (Angles of a triangle)
=> ∠ADB + 35° + 90° = 180°
=> ∠ADB + 125° = 180°
=> ∠ADB = 180° – 125° = 55°
But ∠ACB = ∠ADB (Angles in the same segment of the circle)
∠ACB = 55° Ans.

Question 5.
Solution:
O is the centre of a circle and ∠ACB = 50°
∴ arc AB subtends ∠ AOB at the centre and ∠ ACB at the remaining part of the circle.
∴ ∠ AOB = 2 ∠ ACB
= 2 x 50° = 100
∴ OA = OB (radii of the same circle)
∴ ∠ OAB = ∠ OBA (Angles opposite to equal sides)
Now in ∆ OAB,
∠ OAB + ∠ OBA + ∠ AOB = 180°
=> ∠ OAB + ∠ OAB + ∠ AOB = 180° (∠OAB = ∠OBA)
=> 2 ∠ OAB + 100°= 180°
=> 2 ∠ OAB = 180° – 100° = 80°
=> ∠OAB = \(\frac { { 80 }^{ o } }{ 2 } \) = 40°
Hence, OAB = 40° Ans.

Question 6.
Solution:
(i) In the figure,
∠ABD = 54° and ∠BCD = 43°
∠BAD = ∠BCD (Angles in the same segment of a circle)
∠BAD = 43°

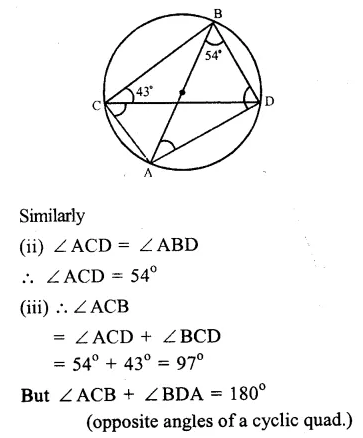
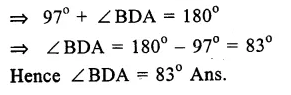
Question 7.
Solution:
Chord DE || diameter AC of the circle with centre O.
∠CBD = 60°
∠CBD = ∠ CAD
(Angles in the same segment of a circle)
∠CAD = 60°
Now in ∆ ADC,

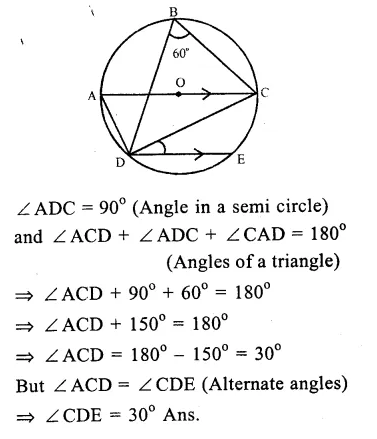
Question 8.
Solution:
In the figure,
chord CD || diameter AB of the circle with centre O.
∠ ABC = 25°
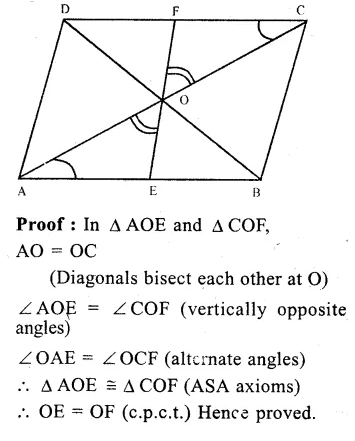
Join CD and DO.
AB || CD
∠ ABC = ∠ BCD (alternate angles)

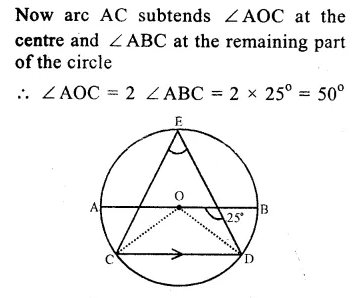
Question 9.
Solution:
AB and CD are two straight lines passing through O, the centre of the circle and ∠AOC = 80°, ∠CDE = 40°
∠ CED = 90° (Angle in a semi circle)

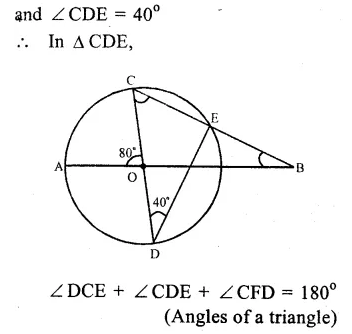
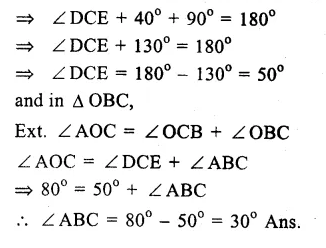
Question 10.
Solution:
O is the centre of the circle and ∠AOB = 40°, ∠BDC = 100°
Arc AB subtends ∠AOB at the centre and ∠ ACB at the remaining part of the circle
∠ AOB = 2 ∠ ACB

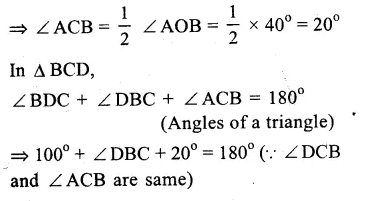
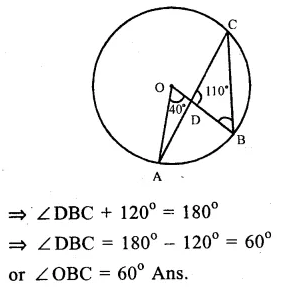
Question 11.
Solution:
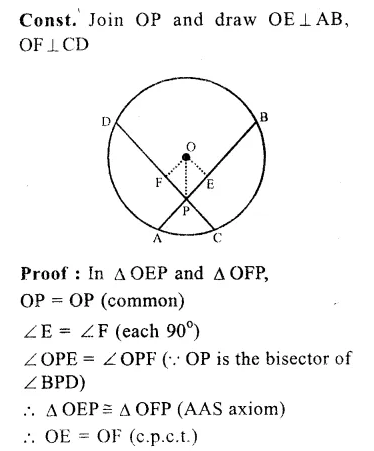
Chords AC and BD of a circle with centre O, intersect each other at E at right angles.
∠ OAB = 25°. Join OB.
In ∆ OAB,
OA = OB (radii of the same circle)

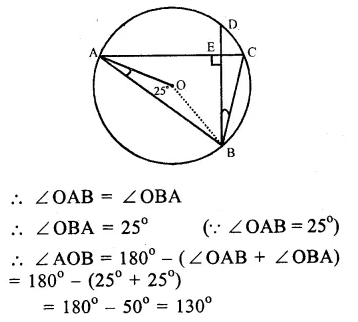
Question 12.
Solution:
In the figure, O is the centre of a circle ∠ OAB = 20° and ∠ OCB = 55° .
In ∆ OAB,

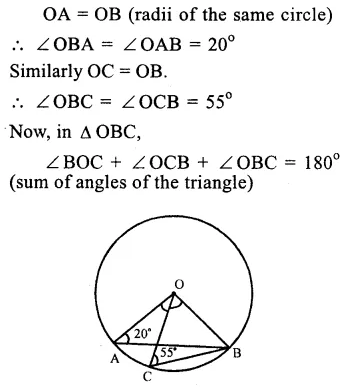
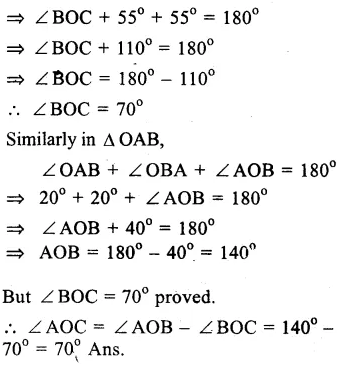
Question 13.
Solution:
Given : A ∆ ABC is inscribed in a circle with centre O and ∠ BAC = 30°
To Prove : BC = radius of the circle
Const. Join OB and OC

Question 14.
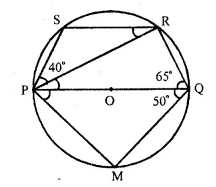
Solution:
In a circle with centre O and PQ is its diameter. ∠PQR = 65°, ∠SPR = 40° and ∠PQM = 50°
(i) ∠PRQ = 90° (Angle in a semicircle) and ∠PQR + ∠RPQ + ∠PQR = 180° (Angles of a triangle)

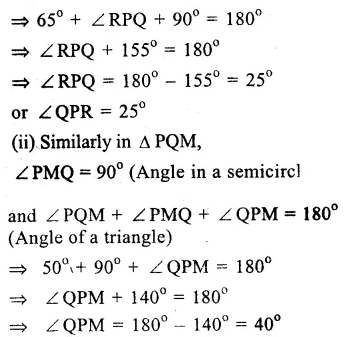
Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C

Question 1.
Solution:
Let AB be a chord of a circle with centre O. OC⊥AB and OA be the radius of the circle, then
AB = 16cm, OA = 10cm .

OC ⊥ AB.
OC bisects AB at C
AC = \(\frac { 1 }{ 2 } \) AB = \(\frac { 1 }{ 2 } \) x 16 = 8cm

Question 2.
Solution:
Let AB be the chord of the circle with centre O and OC ⊥ AB, OA be the radius of the circle,
then OC = 3cm, OA = 5cm

Now in right ∆ OAC,
OA² = AC² = OC² (Pythagoras Theorem)

Question 3.
Solution:
Let AB be the chord, OA be the radius of
the circle OC ⊥ AB
then AB = 30 cm, OC = 8cm

Question 4.
Solution:
AB and CD are parallel chords of a circle with centre O.

Question 5.
Solution:
Let AB and CD be two chords of a circle with centre O.
OA and OC are the radii of the circle. OL⊥AB and OM⊥CD.

Question 6.
Solution:
In the figure, a circle with centre O, CD is its diameter AB is a chord such that CD⊥AB.
AB = 12cm, CE = 3cm.
Join OA.
∵ COD⊥AB which intersects AB at E

Question 7.
Solution:
A circle with centre O, AB is diameter which bisects chord CD at E
i.e. CE = ED = 8cm and EB = 4cm
Join OC.
Let radius of the circle = r

Question 8.
Solution:
Given : O is the centre of a circle AB is a chord and BOC is the diameter. OD⊥AB
To prove : AC || OD and AC = 20D
Proof : OD⊥AB
∵ D is midpoint of AB

Question 9.
Solution:
Given : O is the centre of the circle two
chords AB and CD intersect each other at P inside the circle. PO bisects ∠BPD.
To prove : AB = CD.

Question 10.
Solution:
Given : PQ is the diameter of the circle with centre O which is perpendicular to one chord AB and chord AB || CD.
PQ intersects AB and CD at E and F respectively
To prove : PQ⊥CD and PQ bisects CD.

Question 11.
Solution:
Two circles with centre O and O’ intersect each other.

To prove : The two circles cannot intersect each other at more than two points.
Proof : Let if opposite, the two circles intersect each other at three points P, Q and R.
Then these three points are non-collinear. But, we know that through three non- collinear points, one and only one circle can be drawn.
∵ Our supposition is wrong
Hence two circle can not intersect each other at not more than two points.
Hence proved

Question 12.
Solution:
Given : Two circles with centres O and O’ intersect each other at A and B. AB is a common chord. OO’ is joined.
AO and AO is joined.

Question 13.
Solution:
Given : Two equal circles intersect each other at P and Q.
A straight line drawn through
P, is drawn which meets the circles at A and B respectively
To prove : QA = QB

Question 14.
Solution:
Given : A circle with centre 0. AB and CD are two chords and diameter PQ bisects AB and CD at L and M
To Prove : AB || CD.

Question 15.
Solution:
Given : Two circles with centres A and B touch each other at C internally. A, B arc joined. PQ is the perpendicular bisector of AB intersecting it at L and meeting the bigger circle at P and Q respectively and radii of the circles are 5cm and 3cm. i.e. AC = 5cm,BC = 3cm
Required : To find the lenght of PQ

Question 16.
Solution:
Given : AB is a chord of a circle with centre O. AB is produced to C such that BC = OB, CO is joined and produced to meet the circle at D.
∠ ACD = y°, ∠ AOD = x°
To prove : x = 3y

Question 17.
Solution:
Given : O is the centre of a circle AB and AC are two chords such that AB = AC
OP⊥AB and OQ⊥AC.
which intersect AB and AC at M and N
respectively. PB and QC are joined.
To prove : PB = QC.

Question 18.
Solution:
Given : In a circle with centre O, BC is its diameter. AB and CD are two chords such that AB || CD.
To prove : AB = CD
Const. Draw OL⊥AB
OM⊥CD.
Proof : In ∆ OLB and ∆ OCM,
OB = OC (radii of the same circle)
∠ OLB = ∠ OMC (each 90°)
∠ OBL = ∠ OCM (alternate angles)

Question 19.
Solution:
Equilateral ∆ ABC in inscribed in a circle in which
AB = BC = CA = 9cm.

Question 20.

Solution:
Given : AB and AC are two equal chords of a circle with centre O
To Prove : O lies on the bisector of ∠ BAC

Question 21.
Solution:
Given : OPQR is a square with centre O, a circle is drawn which intersects the square at X and Y.
To Prove : Q = QY
Const. Join OX and OY

Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A.

Question 1.
Solution:
Given : In the figure, ABCD is a quadrilateral and
AB = CD = 5cm

Question 2.
Solution:
In ||gm ABCD,
AB = 10cm, altitude DL = 6cm
and BM is altitude on AD, and BM = 8 cm.

Question 3.
Solution:
Diagonals of rhombus are 16cm and 24 cm.
Area = \(\frac { 1 }{ 2 } \) x product of diagonals
= \(\frac { 1 }{ 2 } \) x 1st diagonal x 2nd diagonal
= \(\frac { 1 }{ 2 } \) x 16 x 24
= 192 cm² Ans.

Question 4.
Solution:
Parallel sides of a trapezium are 9cm and 6cm and distance between them is 8cm

Question 5.
Solution:
from the figure
(i) In ∆ BCD, ∠ DBC = 90°

Question 6.
Solution:
In the fig, ABCD is a trapezium. AB || DC
AB = 7cm, AD = BC = 5cm.
Distance between AB and DC = 4 cm.
i.e. ⊥AL = ⊥BM = 4cm.

Question 7.
Solution:
Given : In quad. ABCD. AL⊥BD and CM⊥BD.
To prove : ar(quad. ABCD)

Question 8.
Solution:
In quad. ABCD, BD is its diagonal and AL⊥BD, CM⊥BD

Question 9.
Solution:
Given : ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect each other at O.
To prove : ar(∆ AOD) = ar(∆ BOC)

Question 10.
Solution:
Given : In the figure,
DE || BC.

Question 11.
Solution:
Given : In ∆ ABC, D and E are the points on AB and AC such that
ar( ∆ BCE) = ar( ∆ BCD)
To prove : DE || BC.
Proof : (∆ BCE) = ar(∆ BCD)
But these are on the same base BC.
Their altitudes are equal.
Hence DE || BC
Hence proved.

Question 12.
Solution:
Given : In ||gm ABCD, O is any. point inside the ||gm. OA, OB, OC and OD are joined.

Question 13.
Solution:
Given : In quad. ABCD.
A line through D, parallel to AC, meets ‘BC produced in P. AP in joined which intersects CD at E.
To prove : ar( ∆ ABP) = ar(quad. ABCD).
Const. Join AC

Question 14.
Solution:
Given : ∆ ABC and ∆ DBC are on the same base BC with points A and D on , opposite sides of BC and
ar( ∆ ABC) = ar( ∆ DBC).

Question 15.
Solution:
Given : In ∆ ABC, AD is the median and P is a point on AD
BP and CP are joined
To prove : (i) ar(∆BDP) = ar(∆CDP)
(ii) ar( ∆ ABP) = ar( ∆ ACP)

Question 16.
Solution:
Given : In quad. ABCD, diagonals AC and BD intersect each other at O and BO = OD
To prove : ar(∆ ABC) = ar(∆ ADC)
Proof : In ∆ ABD,

Question 17.
Solution:
In ∆ ABC,D is mid point of BC
and E is midpoint of AD and BE is joined.

Question 18.
Solution:
Given : In ∆ ABC. D is a point on AB and AD is joined. E is mid point of AD EB and EC are joined.
To prove : ar( ∆ BEC) = \(\frac { 1 }{ 2 } \) ar( ∆ ABC)
Proof : In ∆ ABD,
E is midpoint of AD
BE is its median
ar(∆ EBD) = ar(∆ ABE)

Question 19.
Solution:
Given : In ∆ ABC, D is midpoint of BC and E is die midpoint of BO is the midpoint of AE.
To prove that ar( ∆ BOE) = \(\frac { 1 }{ 8 } \) ar(∆ ABC).

Question 20.
Solution:
Given : In ||gm ABCD, O is any point on diagonal AC.
To prove : ar( ∆ AOB) = ar( ∆ AOD)
Const. Join BD which intersects AC at P
Proof : In ∆ OBD,
P is midpoint of BD
(Diagonals of ||gm bisect each other)

Question 21.
Solution:
Given : ABCD is a ||gm.
P, Q, R and S are the midpoints of sides AB, BC, CD, DA respectively.
PQ, QR, RS and SP are joined.

Question 22.
Solution:
Given : In pentagon ABCDE,
EG || DA meets BA produced and
CF || DB, meets AB produced.
To prove : ar(pentagon ABCDE) = ar(∆ DGF)

Question 23.
Solution:
Given ; A ∆ ABC in which AD is the median.
To prove ; ar( ∆ ABD) = ar( ∆ ACD)
Const : Draw AE⊥BC.
Proof : Area of ∆ ABD

Question 24.
Solution:
Given : A ||gm ABCD in which AC is its diagonal which divides ||gm ABCD in two ∆ ABC and ∆ ADC.

Question 25.
Solution:
Given : In ∆ ABC,
D is a point on BC such that
BD = \(\frac { 1 }{ 2 } \) DC
AD is joined.

Question 26.
Solution:
Given : In ∆ ABC, D is a point on BC such that
BD : DC = m : n
AD is joined.

Hope given RS Aggarwal Class 9 Solutions Chapter 10 Area Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9C

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9C.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9A
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9B
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9C

Question 1.
Solution:
Given : In trapezium ABCD,
AB || DC and E is the midpoint of AD.
A line EF ||AB is drawn meeting BC at F.
To prove : F is midpoint of BC

Question 2.
Solution:
Given : In ||gm ABCD, E and F are the mid points of AB and CD respectively. A line segment GH is drawn which intersects AD, EF and BC at G, P and H respectively.
To prove : GP = PH

Question 3.
Solution:
Given : In trapezium ABCD, AB || DC
P, Q are the midpoints of sides AD and BC respectively
DQ is joined and produced to meet AB produced at E
Join AC which intersects PQ at R.

Question 4.
Solution:
Given : In ∆ ABC,
AD is the mid point of BC
DE || AB is drawn. BE is joined.
To prove : BE is the median of ∆ ABC.
Proof : In ∆ ABC

Question 5.
Solution:
Given : In ∆ ABC, AD and BE are the medians. DF || BE is drawn meeting AC at F.
To prove : CF = \(\frac { 1 }{ 4 } \) BC.

Question 6.
Solution:
Given : In ||gm ABCD, E is mid point of DC.
EB is joined and through D, DEG || EB is drawn which meets CB produced at G and cuts AB at F.
To prove : (i)AD = \(\frac { 1 }{ 2 }\) GC

Question 7.
Solution:

Given : In ∆ ABC,
D, E and F are the mid points of sides BC, CA and AB respectively
DE, EF and FD are joined.

Question 8.
Solution:
Given : In ∆ ABC, D, E and F are the mid points of sides BC, CA and AB respectively

Question 9.
Solution:
Given : In rectangle ABCD, P, Q, R and S are the midpoints of its sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined.
To prove : PQRS is a rhombus.

Question 10.
Solution:
Given : In rhombus ABCD, P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively PQ, QR, RS and SP are joined.

Question 11.
Solution:
Given : In square ABCD, P,Q,R and S are the mid points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.

Question 12.
Solution:
Given : In quadrilateral ABCD, P, Q, R and S are the midpoints of PQ, QR, RS and SP respectively PR and QS are joined.
To prove : PR and QS bisect each other
Const. Join PQ, QR, RS and SP and AC
Proof : In ∆ ABC,


But diagonals of a ||gm bisect each other PR and QS bisect each other.
∴ PR and QS bisect each other

Question 13.
Solution:
Given : ABCD is a quadrilateral. Whose diagonals AC and BD intersect each other at O at right angles.
P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively. PQ, QR, QS and SP are joined.

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9A
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9B
• RS Aggarwal Solutions Class 9 Chapter 9 Quadrilaterals and Parallelograms Ex 9C

Question 1.
Solution:
In parallelogram ABCD.
∠ A = 72°
But ∠ A = ∠ C (opposite angle of a ||gm)
∴ ∠ C = 72°
∴ AD || BC
∴ ∠ A + ∠ B = 180° (co-interior angles)
=> 72° + ∠B = 180°
=> ∠B = 180° – 72°
=> ∠B = 108°
But ∠ B = ∠ D (opposite angles of a ||gm)
∴ ∠D = 108°
Hence ∠D = 108°, ∠ C = 72° and ∠ D = 108° Ans.

Question 2.
Solution:
In || gm ABCD, BD is its diagonal
and ∠DAB = 80° and ∠DBC = 60°
∴AB || DC
∴∠DAB + ∠ADC – 180°
(co-interior angles)
=> 80° + ∠ADC = 180°
=> ∠ ADC = 180° – 80°
=> ∠ ADC = 100°
But ∠ ADB = ∠ DBC (Alternate angles)
∴∠ ADB = 60°
But ∠ ADB + ∠ CDB = 100°
(∴∠ ADC = 100°)
60° + ∠CDB = 100°
=> ∠CDB = 100° – 60° = 40°
Hence ∠CDB = 40° and ∠ ADB = 60° Ans.

Question 3.
Solution:
Given : In ||gm ABCD,
∠ A = 60° Bisectors of ∠ A and ∠ B meet DC at P.
To Prove : (i) ∠APB = 90°
(ii) AD = DP and PB = PC = BC
(iii) DC = 2AD
Proof: ∴ AD || B (opposite sides of a ||gm)
∴∠ A + ∠ B = 180° (co-interior angles)
But AP and BP are the bisectors of ∠A and ∠B
∴\(\frac { 1 }{ 2 } \)∠A + \(\frac { 1 }{ 2 } \) ∠B = 90°

=> ∠PAB + ∠PBA = 90°
But in ∆ APB,
∠PAB + ∠PBA + ∠APB = 180° (angles of a triangle)
=> 90° + ∠APB = 180°
=> ∠APB = 180° – 90° = 90°
Hence ∠APB = 90°
(ii) ∠ A + ∠ D = 180° (co-interior angles)
and ∠ A – 60°
∴ ∠D = 180° – 60° = 120°
But ∠DAP = \(\frac { 1 }{ 2 } \) ∠A = \(\frac { 1 }{ 2 } \) x 60° = 30°
∴∠DPA = 180° – (∠DAP + ∠D)
= 180° – (30° + 120°)
= 180° – 150° = 30°
∠DAP = ∠DPA (each = 30°)
Hence AD = DP (sides opposite to equal angles)
In ∆ BCP,
∠ C = 60° (opposite to ∠ A)
∠CBP = \(\frac { 1 }{ 2 } \) ∠ B = \(\frac { 1 }{ 2 } \) x 120° = 60°
But ∠CPB + ∠CBP + ∠C = 180°
(Angles of a triangle)
=> ∠CPB + 60° + 60° = 180°
=> ∠CPB + 120° = 180°
=> ∠CPB = 180° – 120° = 60°
∆ CBP is an equilateral triangle and BC = CP = BP
=> PB – PC = BC
(iii) DC = DP + PC
= AD + BC
(∴ DP = AD and PC = BC proved)
= AD + AD (∴ AD = BC opposite sides of a ||gm)
= 2AD
Hence DC = 2AD.
Hence proved.

Question 4.
Solution:
In ||gm ABCD,
AC and BD are joined
∠BAO = 35°, ∠ DAO = 40°
∠COD = 105°
∴ ∠AOB = ∠COD
(vertically opposite angles)
∴∠AOB = 105°
(i) Now in ∆ AOB,
∠ABO + ∠AOB + ∠OAB = 180°
(angles of a triangle)
=> ∠ABO + 105° + 35° = 180°
=> ∠ABO + 140° = 180°
=> ∠ABO = 180° – 140°
∠ ABO = 40°
(ii) ∴ AB || DC
∴ ∠ ABO = ∠ ODC (alternate angles)
∴ ∠ ODC = 40°
(iii) ∴ AD || BC
∴ ∠ ACB = ∠ DAO or ∠ DAC
(alternate angles)
= 40°
(iv) ∴ ∠ A + ∠ B = 180° (co-interior angles)
=> (40° + 35°) + ∠B = 180°
=> ∠B = 180° – 75° = 105°
=> ∠ CBD + ∠ABO = 105°
=> ∠CBD + 40° = 105°
=> ∠CBD = 105° – 40° = 65°
Hence ∠ CBD = 65° Ans.

Question 5.
Solution:
In ||gm ABCD
( ∠A = (2x + 25)° and ∠ B = (3x – 5)°
∴AD || BC (opposite sides of parallelogram)
∴∠ A + ∠B = 180° (co-interior angles)
=> 2x + 25° + 3x – 5° = 180°
=> 5x + 20° = 180°
=> 5x = 180° – 20°

=> 5x = 160° => x = \(\frac { { 160 }^{ o } }{ 5 } \) = 32°
∴x = 32°
Now ∠A = 2x + 25° = 2 x 32° + 25°
= 64° + 25° = 89°
∠B = 3x – 5 = 3 x 32° – 5°
= 96° – 5° = 91°
∠ C = ∠ A (∴ opposite angles of ||gm)
= 89°
Similarly ∠B = ∠D
∠D = 91°
Hence ∠ A = 89°, ∠ B = 91°, ∠ C = 89°, ∠D = 91° Ans.

Question 6.
Solution:
Let ∠A and ∠B of a ||gm ABCD are adjacent angles.
∠A + ∠B = 180°
Let ∠B = x

Then ∠ A = \(\frac { 4 }{ 5 } \) x
∴ x + \(\frac { 4 }{ 5 } \) x = 180°
\(\frac { 9 }{ 5 } \) x = 180°
=>\(\frac { { 180 }^{ o }\quad X\quad 5 }{ 9 } \) = 100°
∴ ∠A = \(\frac { 4 }{ 5 } \) x 100° = 80°
and ∠B = 100°
But ∠ C = ∠ A and ∠ D = ∠ B
(opposite angles of a || gm)
∴∠C = 80°, and ∠D = 100°
Hence ∠A = 80°, ∠B = 100°, ∠C = 80° and ∠ D = 100° Ans.

Question 7.
Solution:
Let the smallest angle ∠ A and the other angle ∠ B
Let ∠ A = x
Then ∠ B = 2x – 30°
But ∠ A + ∠ B = 180° (co-interior angles)
∴x + 2x – 30° = 180°
=> 3x = 180° + 30° = 210°
=> x = \(\frac { { 210 }^{ o } }{ 3 } \) = 70°
∴ ∠ A = 70°

and ∠ B = 2x – 30° = 2 x 70° – 30°
= 140° – 30° = 110°
But ∠C = ∠ A and ∠D = ∠B
(opposite angles of a ||gm)
∠C = 70° and ∠D = 110°
Hence ∠A = 70°, ∠B = 110°, ∠C = 70° and ∠D = 110° Ans.

Question 8.
Solution:
In ||gm ABCD,
AB = 9.5 cm and perimeter = 30 cm
=> AB + BC + CD + DA = 30cm
=> AB + BC + AB + BC = 30 cm
( ∴ AB = CD and BC – DA opposite sides)

=> 2(AB + BC) = 30cm
=> AB + BC = 15cm
=> 9 5cm + BC = 15cm
∴BC = 15cm – 9.5cm = 5.5cm
Hence AB = 9.5cm, BC = 5.5cm,
CD = 9.5cm and DA = 5.5cm Ans.

Question 9.
Solution:
ABCD is a rhombus
AB = BC = CD = DA
(i)∴ AB || DC
∴ ∠ B + ∠ C = 180° (co-interior angles)
=> 110° + ∠C = 180°
=> ∠C = 180° – 110° = 70°

Question 10.
Solution:
In a rhombus,
Diagonals bisect each other at right angles
∴ AC and BC bisect each other at O at right angles.
But AC = 24 cm and BD = 18 cm

Question 11.
Solution:
Let ABCD he the rhombus whose diagonal are AC and BD which bisect each other at right angles at O.

Question 12.
Solution:
ABCD is a rectangle whose diagonals AC and BD bisect each other at O.

Question 13.
Solution:
ABCD is a square. A line CX cuts AB at X and diagonal BD at O such that
∠ COD = 80° and ∠ OXA = x°
∴∠ BOX = ∠ COD
(vertically opposite angles)
∴∠BOX = 80°
∴Diagonal BD bisects ∠ B and ∠ D
∴ ∠ABO or ∠ABD = ∠ ADO or ∠ ADB
∴ ∠OBA or ∠OBX = 45°
Now in ∆ OBX,
Ext. ∠ OXA = ∠ BOX + ∠ OBX
=>x° = 80° + 45° = 125° Ans.

Question 14.
Solution:
Given : In ||gm ABCD, AC is joined. AL ⊥ BD and CM ⊥ BD
To prove :
(i) ∆ ALD ≅ ∆ CMB
(ii) AL = CM
Proof : In ∆ ALD and ∆ BMC
AD = BC (opposite sides of ||gm)
∠L = ∠M (each 90°)
∠ ADL = ∠ CBM (Alternate angles)
∴ ∆ ALD ≅ ∆ BMC. (AAS axiom)
∴ or A ALD ≅ A CMB.
AL = CM (c.p.c.t.) Hence proved.

Question 15.
Solution:
Given : In ∆ ABCD, bisectors of ∠A and ∠B meet each other at P.
To prove : ∠APB = 90°
Proof : AD || BC
∠A + ∠B = .180° (co-interior angles)
PA and PB are the bisectors of ∠ A and ∠B

Question 16.
Solution:
In ||gm ABCD,
P and Q are the points on AD and BC respectively such that AP = \(\frac { 1 }{ 3 } \) AD and CQ = \(\frac { 1 }{ 3 } \) BC

Question 17.
Solution:
Given : In ||gm ABCD, diagonals AC and BD bisect each other at O.
A line segment EOF is drawn, which meet AB at E and DC at F.
To -prove : OE = OF

Question 18.
Solution:
Given : ABCD is a ||gm.
AB is produced to E. Such that AB = BE
DE is joined which intersects BC in O.
To prove : ED bisects BC i.e. BO = OC

Question 19.
Solution:
Given : In ||gm ABCD, E is the midpoint BC
DE is joined and produced to meet AB on producing at F.

Question 20.
Solution:
Given : ∆ ABC and lines are drawn through A, B and C parallel to respectively BC, CA and AB forming ∆ PQR.
To prove : BC = \(\frac { 1 }{ 2 } \) QR

Question 21.
Solution:
Given : In ∆ ABC, parallel lines are drawn through A, B and C respectively to the sides BC, CA and AB intersecting each other at P, Q and R.

Hope given RS Aggarwal Class 9 Solutions Chapter 9 Quadrilaterals and Parallelograms Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.