Maths RD Sharma Solutions Class 9

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Mark the correct alternative in each of the following:
Question 1.
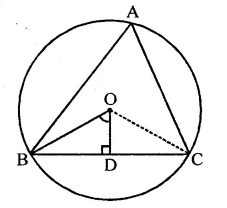
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
(a) 15 cm
(b) 16 cm
(c) 17 cm
(d) 34 cm
Solution:
Length of chord AB of circle = 16 cm
Distance from the centre OL = 15 cm

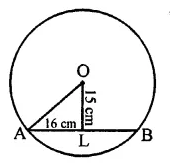
Let OA be the radius, then in right ∆OAL,
OA² = OL² + AL²
16
= (15)² + \(\frac { 16 }{ 2 }\) = 15² + 8²
= 225 + 64 = 289 = (17)²
∴ OA = 17 cm
Hence radius of the circle = 17 cm (c)

Question 2.
The radius of a circle Js 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is

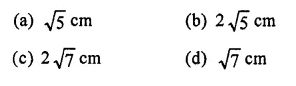
Solution:
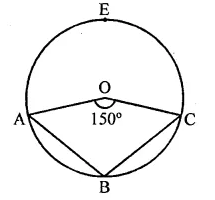
Radius of the cirlce (r) = 6 cm
Perpendicular distance from centre = ?
Length of chord = 8 cm

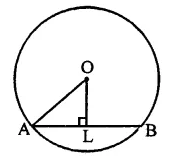
Let AB be chord, OL is the distance
In right ∆OAL
OA² = AL² + OL²

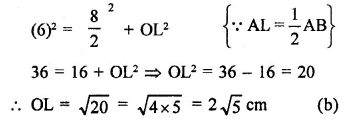
Question 3.
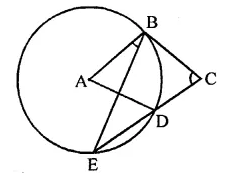
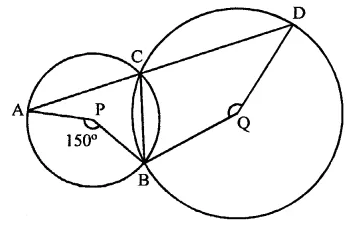
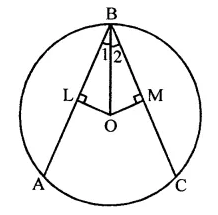
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance \(\frac { r }{ 2 }\) from O, then ∠BAO =
(a) 60°
(b) 45°
(c) 30°
(d) 15°
Solution:
r is the radius of the circle with centre O
AB is the chord, at a distance of \(\frac { r }{ 2 }\) from the centre

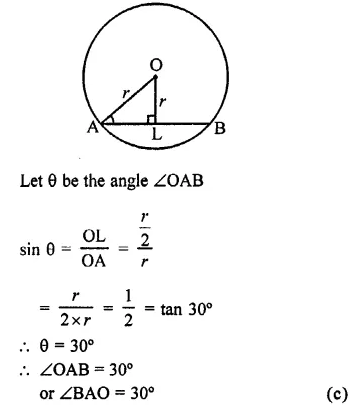
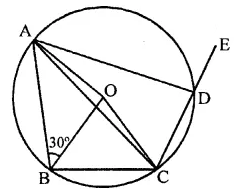
Question 4.
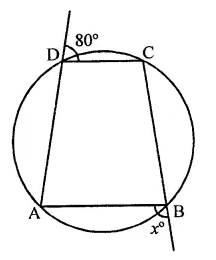
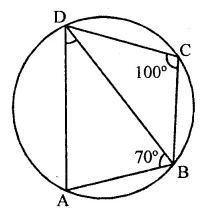
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB=
(a) 70°
(b) 100°
(c) 125°
(d) 150°
Solution:
ABCD is a cyclic quadrilateral ∠DCA = 80° and ∠ADB = 30°

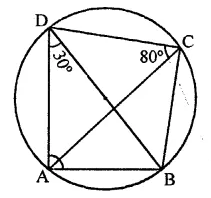
∵∠ADB = ∠ACB (Angles in the same segment)
∴ ∠ACB = 30°
∴ ∠BCD = 80° + 30° = 110°
∵ ABCD is a cyclic quadrilateral
∴∠BAD + ∠BCD = 180°
⇒ ∠BAD + 110°= 180°
⇒ ∠BAD = 180°- 110° = 70°
or ∠DAB = 70° (a)

Question 5.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
(a) 12 cm
(b) 14 cm
(c) 16 cm
(d) 18 cm
Solution:
In a circle AB chord = 14 cm
and distance from centre OL = 6 cm
Let r be the radius of the circle, then OA² = AL² + OL²
⇒ r² = (7)² + (6)² = 49 + 36 = 85

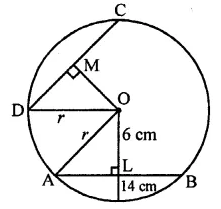
In the same circle length of another chord CD = ?
Distance from centre = 2 cm
∴ r² = OM² + MD²
⇒ 85 = (2)² + DM²
⇒ 85 = 4 + DM²
⇒ DM² = 85-4 = 81 = (9)²
∴ DM = 9
∴ CD = 2 x DM = 2 x 9 = 18 cm
∴Length of another chord = 18 cm (d)

Question 6.
One chord of a circle is known to be 10 cm. The radius of this circle must be
(a) 5 cm
(b) greater than 5 cm
(c) greater than or equal to 5 cm
(d) less than 5 cm
Solution:
Length of chord of a circle = 10 cm
Length of radius of the circle greater than half of the chord
More than \(\frac { 10 }{ 2 }\) = 5 cm (b)

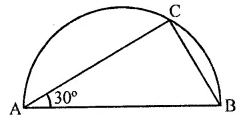
Question 7.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with O as centre and OC as radius. The length of the chord of this circle passing through C and B is
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 6 cm
Solution:
In right ∆ABC, ∠B = 90°
AC = 5 cm, AB = 4 cm

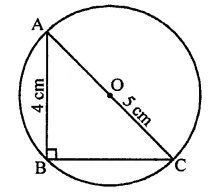
∴ BC² = AC² -AB²
= 5² – 4² = 25 – 16
= 9 = (3)²
∴ BC = 3 cm
∴ Length of chord BC = 3 cm (a)

Question 8.
If AB, BC and CD are equal chords of a circle with O as centre, and AD diameter then ∠AOB =
(a) 60°
(b) 90°
(c) 120°
(d) none of these
Solution:
In a circle chords AB = BC = CD

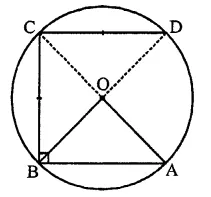
O is the centre of the circle
∴ ∠AOB = cannot be found (d)

Question 9.
Let C be the mid-point of an arc AB of a circle such that m \(\breve { AB }\) = 183°. If the region bounded by the arc ACB and line segment AB is denoted by S, then the centre O of the circle lies
(a) in the interior of S
(b) in the exterior of S
(c) on the segment AB
(d) on AB and bisects AB
Solution:
\(\breve { AB }\) = 183°
∴ AB is the diameter of the circle with centre O and C is the mid point of arc AB

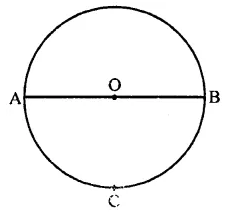
Line segment AB = S
∴ Centre will lie on AB (c)

Question 10.
In a circle, the major arc is 3 ti.nes the minor arc. The corresponding central angles and the degree measures of two arcs are
(a) 90° and 270°
(b) 90° and 90°
(c) 270° adn 90°
(d) 60° and 210°
Solution:
In a circle, major arc is 3 times the minor arc i.e. arc ACB = 3 arc ADB
∴ Reflex ∠AOB = 3∠AOB
But angle at O = 360°

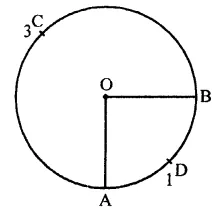
and let ∠AOB = x
Then reflex ∠ADB = x
x + 3x – 360°
⇒ 4x = 360°
⇒ x = \(\frac { { 62 }^{ \circ } }{ 2 }\)  = 90°
∴ 3x = 90° x 3 = 270°
Here angles are 270° and 90° (c)

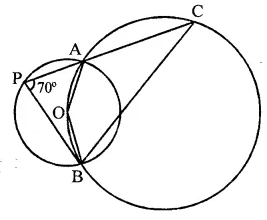
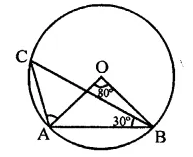
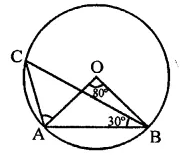
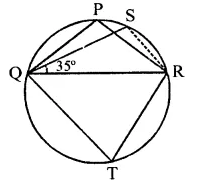
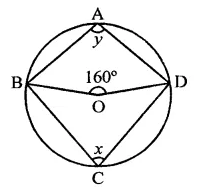
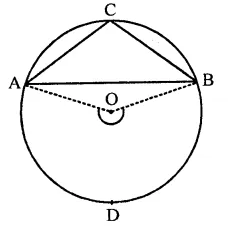
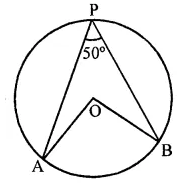
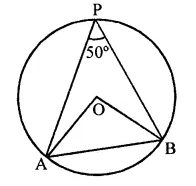
Question 11.
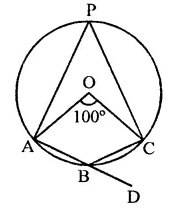
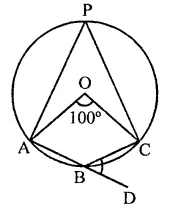
If A and B are two points on a circle such that m(\(\breve { AB }\)) = 260°. A possible value for the angle subtended by arc BA at a point on the circle is
(a) 100°
(b) 75°
(c) 50°
(d) 25°
Solution:
A and B are two points on the circle such that reflex ∠AOB = 260°

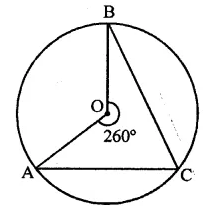
∴ ∠AOB = 360° – 260° = 100°
C is a point on the circle
∴ By joining AC and BC,
∠ACB = \(\frac { 1 }{ 2 }\)∠AOB = \(\frac { 1 }{ 2 }\) x 100° = 50° (c)

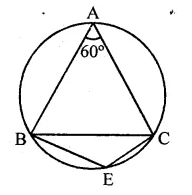
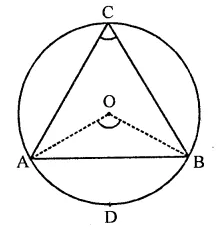
Question 12.
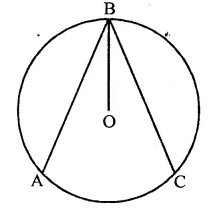
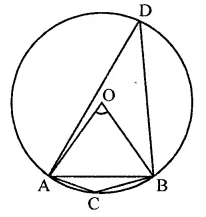
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOC is
(a) 30°
(b) 60°
(c) 90°
(d) 120°
Solution:
∆ABC is an equilateral triangle inscribed in a circle with centre O

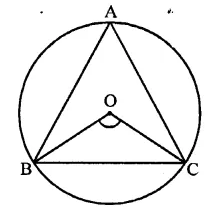
∴ Measure of ∠BOC = 2∠BAC
= 2 x 60° = 120° (d)

Question 13.
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
(a) rhombus
(b) rectangle
(c) parallelogram
(d) square
Solution:
Two diameter of a circle AB and CD intersect each other at right angles

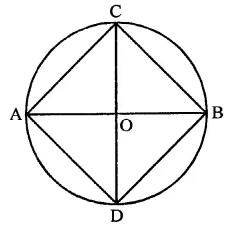
AD, DB, BC and CA are joined forming a quad. ABCD.
∵ The diagonals are equal and bisect each other at right angles
∴ ACBD is a square (d)

Question 14.
In ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \(\breve { AB }\) to the circumference is
(a) 1 : 4
(b) 3 : 4
(c) 3 : 8
(d) 1 : 2
Solution:
Arc ABC of a circle and ∠ABC = 135°
Join OA and OC

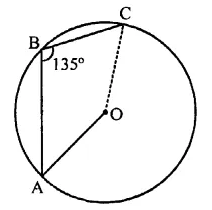
∴ Angle subtended by arc ABC at the centre = 2 x ∠ABC = 2 x 135° = 270°
Angle at the centre of the circle = 360°
∴ Ratio with circumference = 270° : 360° = 3:4 (b)

Question 15.
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
(a) 60°
(b) 75°
(c) 120°
(d) 150°
Solution:
The chord of a circle = radius of the circle In the figure OA = OB = AB

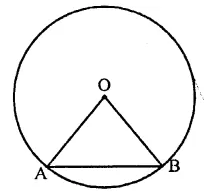
∴ ∠AOB = 60°
(Each angle of an equilateral = 60°) (a)

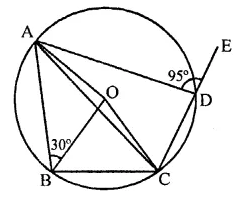
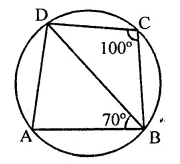
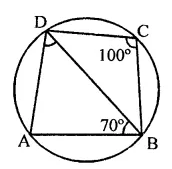
Question 16.
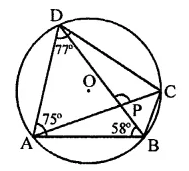
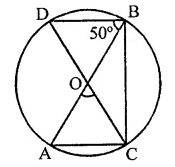
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
(a) 41°
(b) 23°
(c) 67°
(d) 18°
Solution:
PQRS is a cyclic quadrilateral with centre O and ∠QPR = 67°
∠SPR = 72°

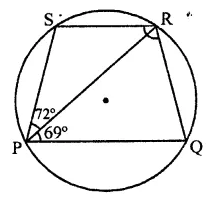
∴ ∠QPS = 67° + 72° = 139°
∵ ∠QPS + ∠QRS = 180° (Sum of opposite angles of a cyclic quad.)
⇒ 139° + ∠QRS = 180°
⇒ ∠QRS = 180° – 139° = 41° (a)

Question 17.
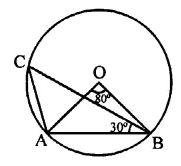
If A, B, C are three points on a circle with centre O such that ∠AOB = 90° and ∠BOC = 120°, then ∠ABC =
(a) 60°
(b) 75°
(c) 90°
(d) 135°
Solution:
A, B and C are three points on a circle with centre O
∠AOB = 90° and ∠BOC = 120°

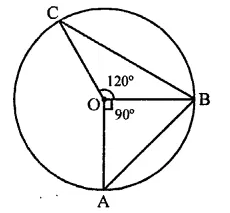
∴ ∠AOC = 360° – (120° + 90°)
= 360° -210°= 150°
But ∠AOC is at the centre made by arc AC and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\) ∠AOC
= \(\frac { 1 }{ 2 }\) x 150° = 75° (b)

Question 18.
The greatest chord of a circle is called its
(a) radius
(b) secant
(c) diameter
(d) none of these
Solution:
The greatest chord of a circle is called its diameter. (c)

Question 19.
Angle formed in minor segment of a circle is
(a) acute
(b) obtuse
(c) right angle
(d) none of these
Solution:
The angle formed in minor segment of a circle is obtuse angle. (b)

Question 20.
Number of circles that can be drawn through three non-collinear points is
(a) 1
(b) 0
(c) 2
(d) 3
Solution:
The number of circles that can pass through three non-collinear points is only one. (a)

Question 21.
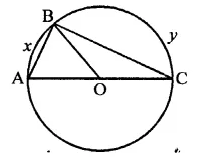
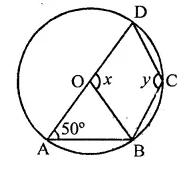
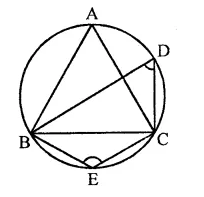
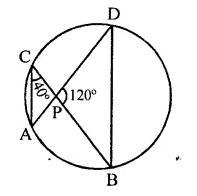
In the figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
(a) 45°
(b) 60°
(c) 75°
(d) 90°

Solution:
In the circle, AB and CD are two chords which intersect each other at P at right angle i.e. ∠CPB = 90°

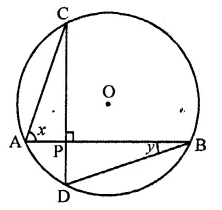
∠CAB and ∠CDB are in the same segment
∴ ∠CDB = ∠CAB = x
Now in ∆PDB,
Ext. ∠CPB = ∠D + ∠DBP
⇒ 90° = x + y (∵ CD ⊥ AB)
Hence x + y = 90° (d)

Question 22.
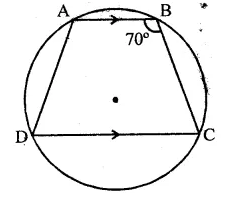
In the figure, if ∠ABC = 45°, then ∠AOC=
(a) 45°
(b) 60°
(c) 75°
(d) 90°

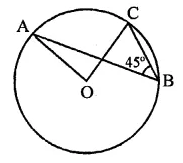
Solution:
∵ arc AC subtends
∠AOC at the centre of the circle and ∠ABC
at the remaining part of the circle

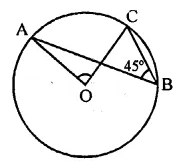
∴ ∠AOC = 2∠ABC
= 2 x 45° = 90°
Hence ∠AOC = 90° (d)

Question 23.
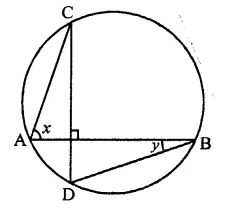
In the figure, chords AD and BC intersect each other at right angles at a point P. If ∠D AB = 35°, then ∠ADC =
(a) 35°
(b) 45°
(c) 55°
(d) 65°

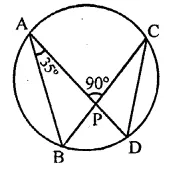
Solution:
Two chords AD and BC intersect each other at right angles at P, ∠DAB = 35°
AB and CD are joined
In ∆ABP,
Ext. ∠APC = ∠B + ∠A

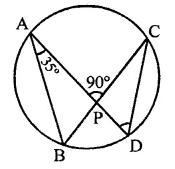
⇒ 90° = ∠B + 35°
∠B = 90° – 35° = 55°
∵ ∠ABC and ∠ADC are in the same segment
∴ ∠ADC = ∠ABC = 55° (c)

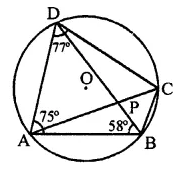
Question 24.
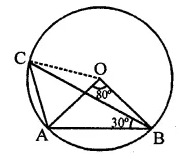
In the figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
(a) 42°
(b) 48°
(c) 58°
(d) 52°

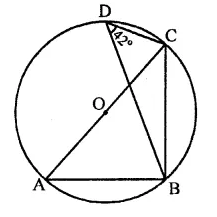
Solution:
In the figure, O is the centre of the circle
∠BDC = 42°
∠ABC = 90° (Angle in a semicircle)
and ∠BAC and ∠BDC are in the same segment of the circle.
∴ ∠BAC = ∠BDC = 42°
Now in ∆ABC,
∠A + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)

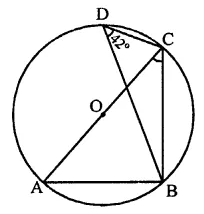
⇒ 42° + 90° + ∠ACB = 180°
⇒ 132° + ∠ACB – 180°
⇒ ∠ACB = 180° – 132° = 48° (b)

Question 25.
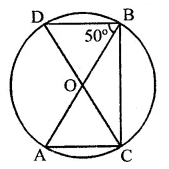
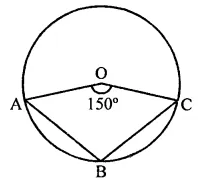
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is

Solution:
AB and CD are two diameters of a circle with centre O

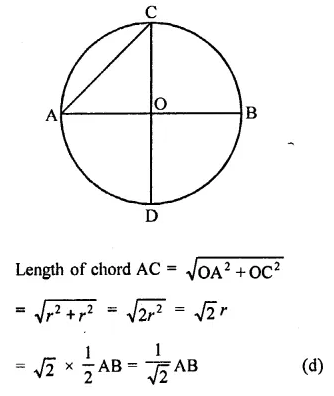
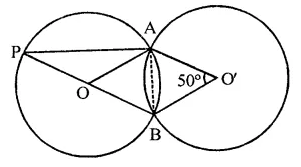
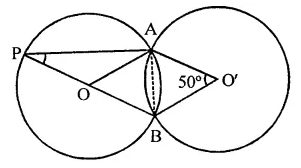
Question 26.
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circles is

Solution:
Two equal circles pass through the centre of the other and intersect each other at A and B
Let r be the radius of each circle

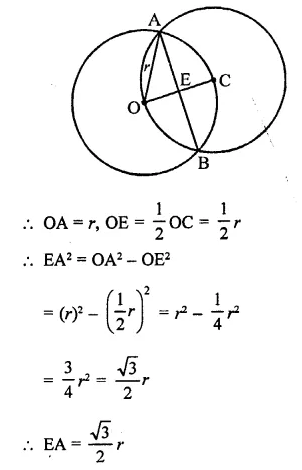
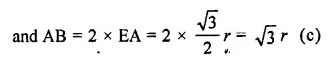
Question 27.
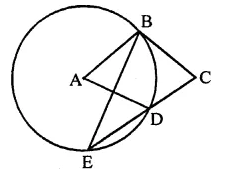
If AB is a chord of a circle, P and Q are the two points on the circle different from A and B,then
(a) ∠APB = ∠AQB
(b) ∠APB + ∠AQB = 180° or ∠APB = ∠AQB
(c) ∠APB + ∠AQB = 90°
(d) ∠APB + ∠AQB = 180°
Solution:
AB is chord of a circle,
P and Q are two points other than from points A and B

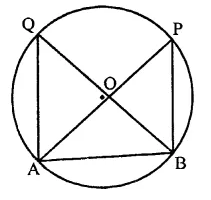
∵ ∠APB and ∠AQB are in the same segment of the circle
∴ ∠APB = ∠AQB (a)

Question 28.
AB and CD are two parallel chords of a circle with centre O such that AB = 6 cm and CD = 12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is

Solution:
AB and CD are two parallel chords of a circle with centre O
Let r be the radius of the circle AB = 6 cm, CD = 12 cm
and distance between them = 3 cm
Join OC and OA, LM = 3 cm

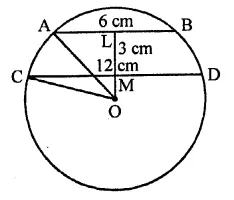
Let OM = x, then OL = x + 3

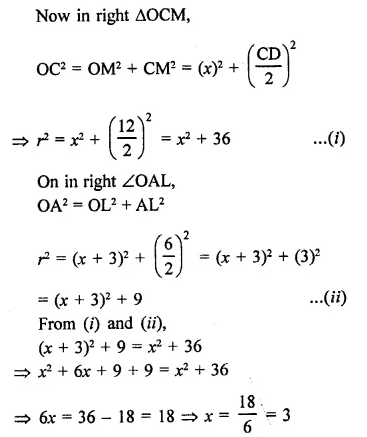
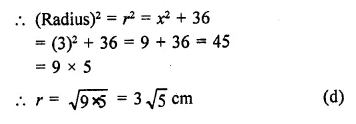
Question 29.
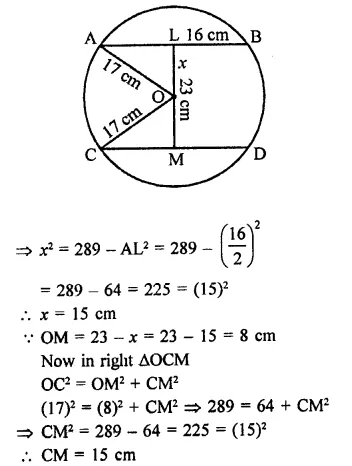
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. This distance between the chords is 23 cm. If the length of one chord is 16 cm then the length of the other is
(a) 34 cm
(b) 15 cm
(c) 23 cm
(d) 30 cm
Solution:
Radius of a circle = 17 cm
The distance between two parallel chords = 23 cm
AB || CD and LM = 23 cm
Join OA and OC,
∴ OA = OC = 17 cm
Let OL = x, then OM = (23 – x) cm
AB = 16 cm
Now in right ∆OAL,
OA² = OL2² + AL²
⇒ (17)² = x² + AL²
⇒ 289 = x² + AL²

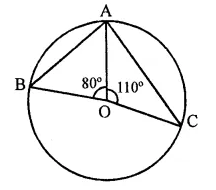
Question 30.
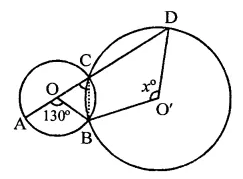
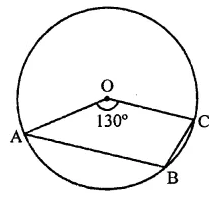
In the figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =
(a) 130°
(b) 115°
(c) 65°
(d) 165°

Solution:
O is the centre of the circle and ∠AOC = 130°
Reflex ∠AOC = 360° – 130° = 230°

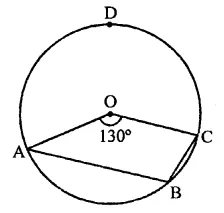
Now arc ADB subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\)reflex ∠AOC
= \(\frac { 1 }{ 2 }\) x 230°= 115° (b)

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, two circles intersect at A and B. The centre of the smaller circle is O and it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.

Solution:
Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴ ∠AOB = 2∠APB = 2 x 70° = 140°
Now in cyclic quadrilateral AOBC,
∠AOB + ∠ACB = 180° (Sum of the angles)
⇒ 140° +∠ACB = 180°
⇒ ∠ACB = 180° – 140° = 40°
∴ ∠ACB = 40°

Question 2.
In the figure, two congruent circles with centre O and O’ intersect at A and B. If ∠AO’B = 50°, then find ∠APB.

Solution:
Two congruent circles with centres O and O’ intersect at A and B

∠AO’B = 50°
∵ OA = OB = O’A = 04B (Radii of the congruent circles)

Question 3.
In the figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = IT, AC and BD intersect at P. Then, find ∠DPC.

Solution:
∵ ABCD is a cyclic quadrilateral,

∴ ∠BAD + ∠BCD = 180°
⇒ 75° + ∠BCD – 180°
⇒ ∠BCD = 180°-75°= 105° and ∠ADC + ∠ABC = 180°
⇒ 77° + ∠ABC = 180°
⇒ ∠ABC = 180°-77°= 103°
∴ ∠DBC = ∠ABC – ∠ABD = 103° – 58° = 45°
∵ Arc AD subtends ∠ABD and ∠ACD in the same segment of the circle 3
∴ ∠ABD = ∠ACD = 58°
∴ ∠ACB = ∠BCD – ∠ACD = 105° – 58° = 47°
Now in ∆PBC,
Ext. ∠DPC = ∠PBC + ∠PCB
=∠DBC + ∠ACB = 45° + 47° = 92°
Hence ∠DPC = 92°

Question 4.
In the figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

Solution:
In the figure, ∠AOB = 80°, ∠ABC = 30°
∵ Arc AB subtends ∠AOB at the centre and
∠ACB at the remaining part of the circle

∴ ∠ACB = \(\frac { 1 }{ 2 }\)∠AOB = \(\frac { 1 }{ 2 }\) x 80° = 40°
In ∆OAB, OA = OB
∴ ∠OAB = ∠OBA
But ∠OAB + ∠OBA + ∠AOB = 180°
∴ ∠OAB + ∠OBA + 80° = 180°
⇒ ∠OAB + ∠OAB = 180° – 80° = 100°
∴ 2∠OAB = 100°
⇒ ∠OAB = \(\frac { { 100 }^{ \circ } }{ 2 }\)  = 50°
Similarly, in ∆ABC,
∠BAC + ∠ACB + ∠ABC = 180°
∠BAC + 40° + 30° = 180°
⇒ ∠BAC = 180°-30°-40°
= 180°-70°= 110°
∴ ∠CAO = ∠BAC – ∠OAB
= 110°-50° = 60°

Question 5.
In the figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

Solution:
In the figure, ABCD is a parallelogram and
CDE is a straight line

∵ ABCD is a ||gm
∴ ∠A = ∠C
and ∠C = ∠ADE (Corresponding angles)
⇒ ∠BCD = ∠ADE
Similarly, ∠ABE = ∠BED (Alternate angles)
∵ arc BD subtends ∠BAD at the centre and
∠BED at the remaining part of the circle

Question 6.
In the figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

Solution:
In the figure, AB is the diameter of the circle such that ∠A = 35° and ∠Q = 25°, join OP.

Arc PB subtends ∠POB at the centre and
∠PAB at the remaining part of the circle
∴ ∠POB = 2∠PAB = 2 x 35° = 70°
Now in ∆OP,
OP = OB radii of the circle
∴ ∠OPB = ∠OBP = 70° (∵ ∠OPB + ∠OBP = 140°)
Now ∠APB = 90° (Angle in a semicircle)
∴ ∠BPQ = 90°
and in ∆PQB,
Ext. ∠PBR = ∠BPQ + ∠PQB
= 90° + 25°= 115°
∴ ∠PBR = 115°

Question 7.
In the figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =

Solution:
In the figure, P and Q are the centres of two circles which intersect each other at C and B
ACD is a straight line ∠APB = 150°
Arc AB subtends ∠APB at the centre and
∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠APB = \(\frac { 1 }{ 2 }\) x 150° = 75°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 75° + ∠BCD = 180°
∠BCD = 180°-75°= 105°
Now arc BD subtends reflex ∠BQD at the centre and ∠BCD at the remaining part of the circle
Reflex ∠BQD = 2∠BCD = 2 x 105° = 210°
But ∠BQD + reflex ∠BQD = 360°
∴ ∠BQD+ 210° = 360°
∴ ∠BQD = 360° – 210° = 150°

Question 8.
In the figure, if O is circumcentre of ∆ABC then find the value of ∠OBC + ∠BAC.

Solution:
In the figure, join OC

∵ O is the circumcentre of ∆ABC
∴ OA = OB = OC
∵ ∠CAO = 60° (Proved)
∴ ∆OAC is an equilateral triangle
∴ ∠AOC = 60°
Now, ∠BOC = ∠BOA + ∠AOC
= 80° + 60° = 140°
and in ∆OBC, OB = OC
∠OCB = ∠OBC
But ∠OCB + ∠OBC = 180° – ∠BOC
= 180°- 140° = 40°
⇒ ∠OBC + ∠OBC = 40°
∴ ∠OBC = \(\frac { { 40 }^{ \circ } }{ 2 }\)  = 20°
∠BAC = OAB + ∠OAC = 50° + 60° = 110°
∴ ∠OBC + ∠BAC = 20° + 110° = 130°

Question 9.
In the AOC is a diameter of the circle and arc AXB = 1/2 arc BYC. Find ∠BOC.

Solution:
In the figure, AOC is diameter arc AxB = \(\frac { 1 }{ 2 }\) arc BYC 1
∠AOB = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠AOB
But ∠AOB + ∠BOC = 180°
⇒ ∠AOB + 2∠AOB = 180°
⇒ 3 ∠AOB = 180°
∴ ∠AOB = \(\frac { { 180 }^{ \circ } }{ 3 }\)  = 60°
∴ ∠BOC = 2 x 60° = 120°

Question 10.
In the figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

Solution:
In the figure, ABCD is a cyclic quadrilateral
CD is produced to E such that ∠ADE = 95°
O is the centre of the circle

∵ ∠ADC + ∠ADE = 180°
⇒ ∠ADC + 95° = 180°
⇒ ∠ADC = 180°-95° = 85°
Now arc ABC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle
∵ ∠AOC = 2∠ADC = 2 x 85° = 170°
Now in ∆OAC,
∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ ∠OAC = ∠OCA (∵ OA = OC radii of circle)
∴ ∠OAC + ∠OAC + 170° = 180°
2∠OAC = 180°- 170°= 10°
∴ ∠OAC = \(\frac { { 10 }^{ \circ } }{ 2 }\) = 5°

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, ∆ABC is an equilateral triangle. Find m ∠BEC.

Solution:
∵ ∆ABC is an equilateral triangle
∴ A = 60°
∵ ABEC is a cyclic quadrilateral
∴ ∠A + ∠E = 180° (Sum of opposite angles)
⇒ 60° + ∠E = 180°
⇒ ∠E = 180° – 60° = 120°
∴ m ∠BEC = 120°

Question 2.
In the figure, ∆PQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.

Solution:
In the figure, ∆PQR is an isosceles PQ = PR
∠PQR = 35°
∴ ∠PRQ = 35°
But ∠PQR + ∠PRQ + ∠QPR = 180° (Sum of angles of a triangle)
⇒ 35° + 35° + ∠QPR = 180°
⇒ 70° + ∠QPR = 180°
∴ ∠QPR = 180° – 70° = 110°
∵ ∠QSR = ∠QPR (Angle in the same segment of circles)
∴ ∠QSR = 110°
But PQTR is a cyclic quadrilateral
∴ ∠QTR + ∠QPR = 180°
⇒ ∠QTR + 110° = 180°
⇒ ∠QTR = 180° -110° = 70°
Hence ∠QTR = 70°

Question 3.
In the figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

Solution:
In the figure, O is the centre of the circle ∠BOD =160°
ABCD is the cyclic quadrilateral
∵ Arc BAD subtends ∠BOD is the angle at the centre and ∠BCD is on the other part of the circle
∴ ∠BCD = \(\frac { 1 }{ 2 }\) ∠BOD
⇒ x = \(\frac { 1 }{ 2 }\) x 160° = 80°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ y + x = 180°
⇒ y + 80° = 180°
⇒ y =180°- 80° = 100°
∴ x = 80°, y = 100°

Question 4.
In the figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

Solution:
In a circle, ABCD is a cyclic quadrilateral ∠BCD = 100° and ∠ABD = 70°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180° (Sum of opposite angles)

⇒ ∠A + 100°= 180°
∠A = 180°- 100° = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180°
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
∴ ∠ADB = 180°- 150° = 30°
Hence ∠ADB = 30°

Question 5.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.

Solution:
Given : ABCD is a cyclic quadrilateral in which AD || BC

To prove : ∠B = ∠C
Proof : ∵ AD || BC
∴ ∠A + ∠B = 180°
(Sum of cointerior angles)
But ∠A + ∠C = 180°
(Opposite angles of the cyclic quadrilateral)
∴ ∠A + ∠B = ∠A + ∠C
⇒ ∠B = ∠C
Hence ∠B = ∠C

Question 6.
In the figure, O is the centre of the circle. Find ∠CBD.

Solution:
Arc AC subtends ∠AOC at the centre and ∠APC at the remaining part of the circle

∴ ∠APC = \(\frac { 1 }{ 2 }\) ∠AOC
= \(\frac { 1 }{ 2 }\) x 100° = 50°
∵ APCB is a.cyclic quadrilateral,
∴ ∠APC + ∠ABC = 180°
⇒ 50° + ∠ABC = 180° ⇒ ∠ABC =180°- 50°
∴ ∠ABC =130°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 130° + ∠CBD = 180°
⇒ ∠CBD = 180°- 130° = 50°
∴ ∠CBD = 50°

Question 7.
In the figure, AB and CD are diameiers of a circle with centre O. If ∠OBD = 50°, find ∠AOC.

Solution:
Two diameters AB and CD intersect each other at O. AC, CB and BD are joined

∠DBA = 50°
∠DBA and ∠DCA are in the same segment
∴ ∠DBA = ∠DCA = 50°
In ∆OAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠DCA = 50°
and ∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ 50° + 50° + ∠AOC = 180°
⇒ 100° + ∠AOC = 180°
⇒ ∠AOC = 180° – 100° = 80°
Hence ∠AOC = 80°

Question 8.
On a semi circle with AB as diameter, a point C is taken so that m (∠CAB) = 30°. Find m (∠ACB) and m (∠ABC).
Solution:
A semicircle with AB as diameter

∠ CAB = 30°
∠ACB = 90° (Angle in a semi circle)
But ∠CAB + ∠ACB + ∠ABC = 180°
⇒ 30° + 90° + ∠ABC – 180°
⇒ 120° + ∠ABC = 180°
∴ ∠ABC = 180°- 120° = 60°
Hence m ∠ACB = 90°
and m ∠ABC = 60°

Question 9.
In a cyclic quadrilateral ABCD, if AB || CD and ∠B = 70°, find the remaining angles.
Solution:
In a cyclic quadrilateral ABCD, AB || CD and ∠B = 70°

∵ ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ 70° + ∠D = 180°
⇒ ∠D = 180°-70° = 110°
∵ AB || CD
∴ ∠A + ∠D = 180° (Sum of cointerior angles)
∠A+ 110°= 180°
⇒ ∠A= 180°- 110° = 70°
Similarly, ∠B + ∠C = 180°
⇒ 70° + ∠C- 180° ‘
⇒ ∠C = 180°-70°= 110°
∴ ∠A = 70°, ∠C = 110°, ∠D = 110°

Question 10.
In a cyclic quadrilateral ABCD, if m ∠A = 3(m ∠C). Find m ∠A.
Solution:
In cyclic quadrilateral ABCD, m ∠A = 3(m ∠C)

∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ 3 ∠C + ∠C = 180° ⇒ 4∠C = 180°
⇒ ∠C = \(\frac { { 180 }^{ \circ } }{ 4 }\)  = 45°
∴ ∠A = 3 x 45°= 135°
Hence m ∠A =135°

Question 11.
In the figure, O is the centre of the circle and ∠DAB = 50°. Calculate the values of x and y.

Solution:
In the figure, O is the centre of the circle ∠DAB = 50°
∵ ABCD is a cyclic quadrilateral
∴ ∠A + ∠C = 180°
⇒ 50° + y = 180°
⇒ y = 180° – 50° = 130°
In ∆OAB, OA = OB (Radii of the circle)
∴ ∠A = ∠OBA = 50°
∴ Ext. ∠DOB = ∠A + ∠OBA
x = 50° + 50° = 100°
∴ x= 100°, y= 130°

Question 12.
In the figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.

Solution:
In ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)

60° + ∠ABC + 20° = 180°
∠ABC + 80° = 180°
∴ ∠ABC = 180° -80°= 100°
∵ ABCD is a cyclic quadrilateral,
∴ ∠ABC + ∠ADC = 180°
100° + ∠ADC = 180°
∴ ∠ADC = 180°- 100° = 80°

Question 13.
In the figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.

Solution:
In a circle, ∆ABC is an equilateral triangle

∴ ∠A = 60°
∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 60°
∵ BECD is a cyclic quadrilateral
∴ ∠BDC + ∠BEC = 180°
⇒ 60° + ∠BEC = 180°
⇒ ∠BEC = 180°-60°= 120°
Hence ∠BDC = 60° and ∠BEC = 120°

Question 14.
In the figure, O is the centre of the circle. If ∠CEA = 30°, find the values of x, y and z.

Solution:
∠AEC and ∠ADC are in the same segment
∴ ∠AEC = ∠ADC = 30°
∴ z = 30°
ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ x + z = 180°
⇒ x + 30° = 180°
⇒ x = 180° – 30° = 150°
Arc AC subtends ∠AOB at the centre and ∠ADC at the remaining part of the circle
∴ ∠AOC = 2∠D = 2 x 30° = 60°
∴ y = 60°
Hence x = 150°, y – 60° and z = 30°

Question 15.
In the figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.

Solution:
In the figure, two circles intersect each other at C and D
∠BAD = 78°, ∠DCF = x, ∠DEF = y
ABCD is a cyclic quadrilateral
∴ Ext. ∠DCF = its interior opposite ∠BAD
⇒ x = 78°
In cyclic quadrilateral CDEF,
∠DCF + ∠DEF = 180°
⇒ 78° + y = 180°
⇒ y = 180° – 78°
y = 102°
Hence x = 78°, and y- 102°

Question 16.
In a cyclic quadrilateral ABCD, if ∠A – ∠C = 60°, prove that the smaller of two is 60°.
Solution:
In cyclic quadrilateral ABCD,
∠A – ∠C = 60°
But ∠A + ∠C = 180° (Sum of opposite angles)

Adding, 2∠A = 240° ⇒ ∠A = \(\frac { { 62 }^{ \circ } }{ 2 }\)  = 120° and subtracting
2∠C = 120° ⇒ ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\)  = 60°
∴ Smaller angle of the two is 60°.

Question 17.
In the figure, ABCD is a cyclic quadrilateral. Find the value of x.

Solution:
∠CDE + ∠CDA = 180° (Linear pair)
⇒ 80° + ∠CDA = 180°
⇒ ∠CDA = 180° – 80° = 100°

In cyclic quadrilateral ABCD,
Ext. ∠ABF = Its interior opposite angle ∠CDA = 100°
∴ x = 100°

Question 18.
ABCD is a cyclic quadrilateral in which:
(i) BC || AD, ∠ADC =110° and ∠B AC = 50°. Find ∠DAC.
(ii) ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
(iii) ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.
Solution:
(i) In the figure,

ABCD is a cyclic quadrilateral and AD || BC, ∠ADC = 110°
∠BAC = 50°
∵ ∠B + ∠D = 180° (Sum of opposite angles)
⇒ ∠B + 110° = 180°
∴ ∠B = 180°- 110° = 70°
Now in ∆ABC,
∠CAB + ∠ABC + ∠BCA = 180° (Sum of angles of a triangle)
⇒ 50° + 70° + ∠BCA = 180°
⇒ 120° + ∠BCA = 180°
⇒ ∠BCA = 180° – 120° = 60°
But ∠DAC = ∠BCA (Alternate angles)
∴ ∠DAC = 60°
(ii) In cyclic quadrilateral ABCD,
Diagonals AC and BD are joined ∠DBC = 80°, ∠BAC = 40°

Arc DC subtends ∠DBC and ∠DAC in the same segment
∴ ∠DBC = ∠DAC = 80°
∴ ∠DAB = ∠DAC + ∠CAB = 80° + 40° = 120°
But ∠DAC + ∠BCD = 180° (Sum of opposite angles of a cyclic quad.)
⇒ 120° +∠BCD = 180°
⇒ ∠BCD = 180°- 120° = 60°
(iii) In the figure, ABCD is a cyclic quadrilateral BD is joined
∠BCD = 100°
and ∠ABD = 70°

∠A + ∠C = 180° (Sum of opposite angles of cyclic quad.)
∠A+ 100°= 180°
⇒ ∠A= 180°- 100°
∴ ∠A = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
⇒ ∠ADB = 180°- 150° = 30°
∴ ∠ADB = 30°

Question 19.
Prove that the circles described on the four sides of a rhombus as diameter, pass through the point of intersection of its diagonals.
Solution:
Given : ABCD is a rhombus. Four circles are drawn on the sides AB, BC, CD and DA respectively

To prove : The circles pass through the point of intersection of the diagonals of the rhombus ABCD
Proof: ABCD is a rhombus whose diagonals AC and BD intersect each other at O
∵ The diagonals of a rhombus bisect each other at right angles
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Now when ∠AOB = 90°
and a circle described on AB as diameter will pass through O
Similarly, the circles on BC, CD and DA as diameter, will also pass through O

Question 20.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that is diagonals are equal.
Solution:
Given : In cyclic quadrilateral ABCD, AB = CD
AC and BD are the diagonals

To prove : AC = BC
Proof: ∵ AB = CD
∴ arc AB = arc CD
Adding arc BC to both sides, then arc AB + arc BC = arc BC + arc CD
⇒ arc AC = arc BD
∴ AC = BD
Hence diagonal of the cyclic quadrilateral are equal.

Question 21.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Solution:
Given : In ∆ABC, circles are drawn on sides AB and AC
To prove : Circles drawn on AB and AC intersect at D which lies on BC, the third side
Construction : Draw AD ⊥ BC

Proof: ∵ AD ⊥ BC
∴ ∠ADB = ∠ADC = 90°
So, the circles drawn on sides AB and AC as diameter will pass through D
Hence circles drawn on two sides of a triangle pass through D, which lies on the third side.

Question 22.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Solution:
In the figure, ABCD is a trapezium in which AD || BC and ∠B = 70°

∵ AD || BC
∴ ∠A + ∠B = 180° (Sum of cointerior angles)
⇒ ∠A + 70° = 180°
⇒ ∠A= 180°- 70° = 110°
∴ ∠A = 110°
But ∠A + ∠C = 180° and ∠B + ∠D = 180° (Sum of opposite angles of a cyclic quadrilateral)
∴ 110° + ∠C = 180°
⇒ ∠C = 180°- 110° = 70°
and 70° + ∠D = 180°
⇒ ∠D = 180° – 70° = 110°
∴ ∠A = 110°, ∠C = 70° and ∠D = 110°

Question 23.
In the figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.

Solution:
In the figure, ABCD is a cyclic quadrilateral whose diagonals AC and BD are drawn ∠DBC = 55° and ∠BAC = 45°

∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 45°
Now in ABCD,
∠DBC + ∠BDC + ∠BCD = 180° (Sum of angles of a triangle)
⇒ 55° + 45° + ∠BCD = 180°
⇒ 100° + ∠BCD = 180°
⇒ ∠BCD = 180° – 100° = 80°
Hence ∠BCD = 80°

Question 24.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Solution:
Given : ABCD is a cyclic quadrilateral

To prove : The perpendicular bisectors of the sides are concurrent
Proof : ∵ Each side of the cyclic quadrilateral is a chord of the circle and perpendicular of a chord passes through the centre of the circle
Hence the perpendicular bisectors of each side will pass through the centre O
Hence the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent

Question 25.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
Solution:
Given : ABCD is a cyclic rectangle and diagonals AC and BD intersect each other at O

To prove : O is the point of intersection is the centre of the circle.
Proof : Let O be the centre of the circle- circumscribing the rectangle ABCD
Since each angle of a rectangle is a right angle and AC is the chord of the circle
∴ AC will be the diameter of the circle Similarly, we can prove that diagonal BD is also the diameter of the circle
∴ The diameters of the circle pass through the centre
Hence the point of intersection of the diagonals of the rectangle is the centre of the circle.

Question 26.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that:
(i) AD || BC
(ii) EB = EC.
Solution:
Given : ABCD is a cyclic quadrilateral in which sides BA and CD are produced to meet at E and EA = ED

To prove :
(i) AD || BC
(ii) EB = EC
Proof: ∵ EA = ED
∴ In ∆EAD
∠EAD = ∠EDA (Angles opposite to equal sides)
In a cyclic quadrilateral ABCD,
Ext. ∠EAD = ∠C
Similarly Ext. ∠EDA = ∠B
∵ ∠EAD = ∠EDA
∴ ∠B = ∠C
Now in ∆EBC,
∵ ∠B = ∠C
∴ EC = EB (Sides opposite to equal sides)
and ∠EAD = ∠B
But these are corresponding angles
∴ AD || BC

Question 27.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Solution:
Given : A segment ACB shorter than a semicircle and an angle ∠ACB inscribed in it
To prove : ∠ACB < 90°
Construction : Join OA and OB

Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle ∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB But ∠AOB > 180° (Reflex angle)
∴ ∠ACB > \(\frac { 1 }{ 2 }\) x [80°
⇒ ∠ACB > 90°

Question 28.
Prove that the angle in a segment greater than a semi-circle is less than a right angle
Solution:
Given : A segment ACB, greater than a semicircle with centre O and ∠ACB is described in it
To prove : ∠ACB < 90°
Construction : Join OA and OB

Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠ACB =\(\frac { 1 }{ 2 }\) ∠AOB
But ∠AOB < 180° (A straight angle) 1
∴ ∠ACB < \(\frac { 1 }{ 2 }\) x 180°
⇒ ∠ACB <90°
Hence ∠ACB < 90°

Question 29.
Prove that the line segment joining the mid-point of the hypotenuse of a rijght triangle to its opposite vertex is half of the hypotenuse.
Solution:
Given : In a right angled ∆ABC
∠B = 90°, D is the mid point of hypotenuse AC. DB is joined.
To prove : BD = \(\frac { 1 }{ 2 }\) AC
Construction : Draw a circle with centre D and AC as diameter

Proof: ∵ ∠ABC = 90°
∴ The circle drawn on AC as diameter will pass through B
∴ BD is the radius of the circle
But AC is the diameter of the circle and D is mid point of AC
∴ AD = DC = BD
∴ BD= \(\frac { 1 }{ 2 }\) AC

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

Solution:
Arc AB, subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴∠AOB = 2∠APB = 2 x 50° = 100°
Join AB

∆AOB is an isosceles triangle in which
OA = OB
∴ ∠OAB = ∠OBA But ∠AOB = 100°
∴∠OAB + ∠OBA = 180° – 100° = 80°
⇒ 2∠OAB = 80°
80°
∴∠OAB = \(\frac { { 80 }^{ \circ } }{ 2 }\)  = 40°

Question 2.
In the figure, O is the centre of the circle. Find ∠BAC.

Solution:
In the circle with centre O
∠AOB = 80° and ∠AOC =110°
∴ ∠BOC = ∠AOB + ∠AOC
= 80°+ 110°= 190°
∴ Reflex ∠BOC = 360° – 190° = 170°
Now arc BEC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

∴ ∠BOC = 2∠BAC
⇒ 170° = 2∠BAC
⇒ ∠BAC = \(\frac { { 170 }^{ \circ } }{ 2 }\) = 85°
∴ ∠BAC = 85°

Question 3.
If O is the centre of the circle, find the value of x in each of the following figures:



Solution:
(i) A circle with centre O
∠AOC = 135°
But ∠AOC + ∠COB = 180° (Linear pair)
⇒ 135° + ∠COB = 180°
⇒ ∠COB = 180°- 135° = 45°
Now arc BC subtends ∠BOC at the centre and ∠BPC at the remaining part of the circle
∴ ∠BOC = 2∠BPC
⇒ ∠BPC = \(\frac { 1 }{ 2 }\)∠BOC = \(\frac { 1 }{ 2 }\) x 45° = \(\frac { { 45 }^{ \circ } }{ 2 }\)
∴ ∠BPC = 22 \(\frac { 1 }{ 2 }\)° or x = 22 \(\frac { 1 }{ 2 }\)°
(ii) ∵ CD and AB are the diameters of the circle with centre O
∠ABC = 40°
But in ∆OBC,
OB = OC (Radii of the circle)
∠OCB = ∠OBC – 40°
Now in ABCD,
∠ODB + ∠OCB + ∠CBD = 180° (Angles of a triangle)
⇒ x + 40° + 90° = 180°
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
∴ x = 50°
(iii) In circle with centre O,
∠AOC = 120°, AB is produced to D
∵ ∠AOC = 120°
and ∠AOC + convex ∠AOC = 360°
⇒ 120° + convex ∠AOC = 360°
∴ Convex ∠AOC = 360° – 120° = 240°
∴ Arc APC Subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\)∠AOC = \(\frac { 1 }{ 2 }\)x 240° = 120°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 120° + x = 180°
⇒ x = 180° – 120° = 60°
∴ x = 60°
(iv) A circle with centre O and ∠CBD = 65°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ ∠ABC + 65° = 180°
⇒ ∠ABC = 180°-65°= 115°
Now arc AEC subtends ∠x at the centre and ∠ABC at the remaining part of the circle
∴ ∠AOC = 2∠ABC
⇒ x = 2 x 115° = 230°
∴ x = 230°
(v) In circle with centre O
AB is chord of the circle, ∠OAB = 35°
In ∆OAB,
OA = OB (Radii of the circle)
∠OBA = ∠OAB = 35°
But in ∆OAB,
∠OAB + ∠OBA + ∠AOB = 180° (Angles of a triangle)
⇒ 35° + 35° + ∠AOB = 180°
⇒ 70° + ∠AOB = 180°
⇒ ∠AOB = 180°-70°= 110°
∴ Convex ∠AOB = 360° -110° = 250°
But arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴∠ACB = \(\frac { 1 }{ 2 }\)∠AOB
⇒ x = \(\frac { 1 }{ 2 }\) x 250° = 125°
∴ x= 125°
(vi) In the circle with centre O,
BOC is its diameter, ∠AOB = 60°
Arc AB subtends ∠AOB at the centre of the circle and ∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB
= \(\frac { 1 }{ 2 }\) x 60° = 30°
But in ∆OAC,
OC = OA (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠ACB
⇒ x = 30°
(vii) In the circle, ∠BAC and ∠BDC are in the same segment
∴ ∠BDC = ∠BAC = 50°
Now in ABCD,
∠DBC + ∠BCD + ∠BDC = 180° (Angles of a triangle)
⇒ 70° + x + 50° = 180°
⇒ x + 120° = 180° ⇒ x = 180° – 120° = 60°
∴ x = 60°
(viii) In circle with centre O,
∠OBD = 40°
AB and CD are diameters of the circle
∠DBA and ∠ACD are in the same segment
∴ ∠ACD = ∠DBA = 40°
In AOAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = 40°
and ∠OAC + ∠OCA + ∠AOC = 180° (Angles in a triangle)
⇒ 40° + 40° + x = 180°
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
∴ x = 100°
(ix) In the circle, ABCD is a cyclic quadrilateral ∠ADB = 32°, ∠DAC = 28° and ∠ABD = 50°
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD ⇒ ∠ACD = 50°
Similarly, ∠ADB = ∠ACB
⇒ ∠ACB = 32°
Now, ∠DCB = ∠ACD + ∠ACB
= 50° + 32° = 82°
∴ x = 82°
(x) In a circle,
∠BAC = 35°, ∠CBD = 65°
∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 35°
In ∆BCD,
∠BDC + ∠BCD + ∠CBD = 180° (Angles in a triangle)
⇒ 35° + x + 65° = 180°
⇒ x + 100° = 180°
⇒ x = 180° – 100° = 80°
∴ x = 80°
(xi) In the circle,
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD = 40°
Now in ∆CPD,
∠CPD + ∠PCD + ∠PDC = 180° (Angles of a triangle)
110° + 40° + x = 180°
⇒ x + 150° = 180°
∴ x= 180°- 150° = 30°
(xii) In the circle, two diameters AC and BD intersect each other at O
∠BAC = 50°
In ∆OAB,
OA = OB (Radii of the circle)
∴ ∠OBA = ∠OAB = 52°
⇒ ∠ABD = 52°
But ∠ABD and ∠ACD are in the same segment of the circle
∴ ∠ABD = ∠ACD ⇒ 52° = x
∴ x = 52°

Question 4.
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A.
Solution:
Given : O is the circumcentre of ∆ABC.
OD ⊥ BC
OB is joined
To prove : ∠BOD = ∠A
Construction : Join OC.

Proof : Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle
∴ ∠BOC = 2∠A …(i)
In right ∆OBD and ∆OCD Side OD = OD (Common)
Hyp. OB = OC (Radii of the circle)
∴ ∆OBD ≅ ∆OCD (RHS criterion)
∴ ∠BOD = ∠COD = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠BOD …(ii)
From (i) and (ii)
2∠BOD = 2∠A
∴∠BOD = ∠A

Question 5.
In the figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.

Solution:
Given : In the figure, a circle with centre O OB is the bisector of ∠ABC
To prove : AB = BC
Construction : Draw OL ⊥ AB and OM ⊥ BC

Proof: In ∆OLB and ∆OMB,
∠1 = ∠2 (Given)
∠L = ∠M (Each = 90°)
OB = OB (Common)
∴ ∆OLB ≅ ∆OMB (AAS criterion)
∴ OL = OM (c.p.c.t.)
But these are distance from the centre and chords equidistant from the centre are equal
∴ Chord BA = BC
Hence AB = BC

Question 6.
In the figure, O and O’ are centres of two circles intersecting at B and C. ACD is a straight line, find x.

Solution:
In the figure, two circles with centres O and O’ intersect each other at B and C.
ACD is a line, ∠AOB = 130°
Arc AB subtends ∠AOB at the centre O and ∠ACB at the remaining part of the circle.

∴ ∠ACB =\(\frac { 1 }{ 2 }\)∠AOB
= \(\frac { 1 }{ 2 }\) x 130° = 65°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 65° + ∠BCD = 180°
⇒ ∠BCD = 180°-65°= 115°
Now, arc BD subtends reflex ∠BO’D at the centre and ∠BCD at the remaining part of the circle
∴ ∠BO’D = 2∠BCD = 2 x 115° = 230°
But ∠BO’D + reflex ∠BO’D = 360° (Angles at a point)
⇒ x + 230° = 360°
⇒ x = 360° -230°= 130°
Hence x = 130°

Question 7.
In the figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.

Solution:
Arc AB subtend ∠ACB and ∠ADB in the same segment of a circle
∴ ∠ACB = ∠ADB = 40°
In ∆PDB,
∠DPB + ∠PBD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 120° + ∠PBD + 40° = 180°
⇒ 160° + ∠PBD = 180°
⇒ ∠PBD = 180° – 160° = 20°
⇒ ∠CBD = 20°

Question 8.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
A circle with centre O, a chord AB = radius of the circle C and D are points on the minor and major arcs of the circle

∴ ∠ACB and ∠ADB are formed Now in ∆AOB,
OA = OB = AB (∵ AB = radii of the circle)
∴ ∆AOB is an equilateral triangle,
∴ ∠AOB = 60°
Now arc AB subtends ∠AOB at the centre and ∠ADB at the remainder part of the circle.
∴ ∠ADB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\)x 60° = 30°
Now ACBD is a cyclic quadrilateral,
∴ ∠ADB + ∠ACB = 180° (Sum of opposite angles of cyclic quad.)
⇒ 30° + ∠ACB = 180°
⇒ ∠ACB = 180° – 30° = 150°
∴ ∠ACB = 150°
Hence angles are 150° and 30°

Question 9.
In the figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

Solution:
In circle with centre O and ∠AOC = 150°
But ∠AOC + reflex ∠AOC = 360°
∴ 150° + reflex ∠AOC = 360°
⇒ Reflex ∠AOC = 360° – 150° = 210°
Now arc AEC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

Reflex ∠AOC = 2∠ABC
⇒ 210° = 2∠ABC
∴ ∠ABC = \(\frac { { 210 }^{ \circ } }{ 2 }\)  = 105°

Question 10.
In the figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Solution:
Given : In circle, O is centre

To prove : ∠x = ∠y + ∠z
Proof : ∵ ∠3 and ∠4 are in the same segment of the circle
∴ ∠3 = ∠4 …(i)
∵ Arc AB subtends ∠AOB at the centre and ∠3 at the remaining part of the circle
∴ ∠x = 2∠3 = ∠3 + ∠3 = ∠3 + ∠4 (∵ ∠3 = ∠4) …(ii)
In ∆ACE,
Ext. ∠y = ∠3 + ∠1
(Ext. is equal to sum of its interior opposite angles)
⇒ ∠3 – ∠y – ∠1 …(ii)
From (i) and (ii),
∠x = ∠y – ∠1 + ∠4 …(iii)
Similarly in ∆ADF,
Ext. ∠4 = ∠1 + ∠z …(iv)
From (iii) and (iv)
∠x = ∠y-∠l + (∠1 + ∠z)
= ∠y – ∠1 + ∠1 + ∠z = ∠y + ∠z
Hence ∠x = ∠y + ∠z

Question 11.
In the figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.

Solution:
In the figure, O is the centre of the circle,
PQ is the diameter and ∠ROS = 40°
Now we have to find ∠RTS
Arc RS subtends ∠ROS at the centre and ∠RQS at the remaining part of the circle

∴ ∠RQS = \(\frac { 1 }{ 2 }\) ∠ROS
= \(\frac { 1 }{ 2 }\) x 40° = 20°
∵ ∠PRQ = 90° (Angle in a semi circle)
∴ ∠QRT = 180° – 90° = 90° (∵ PRT is a straight line)
Now in ∆RQT,
∠RQT + ∠QRT + ∠RTQ = 180° (Angles of a triangle)
⇒ 20° + 90° + ∠RTQ = 180°
⇒ ∠RTQ = 180° – 20° – 90° = 70° or ∠RTS = 70°
Hence ∠RTS = 70°

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius 20 m drawn in a park. Ishita throws a ball to Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is 24 m each, what is the distance between Ishita and Nisha. [NCERT]
Solution:
∵ Distance between Isha and Ishita and Ishita and Nisha is same
∴ RS = SM = 24 m
∴They are equidistant from the centre
In right ∆ORL,
OL² = OR² – RL²


Hence distance between Ishita and Nisha = 38.4 m

Question 2.
A circular park of radius 40 m is situated in a colony. Three beys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find thelength of the string of each phone. [NCERT]
Solution:
Radius of circular park = 40 m
Ankur, Amit and Anand are sitting at equal distance to each other By joining them, an equilateral triangle ABC is formed produce BO to L which is perpendicular bisector of AC

∴ BL = 40 + 20 = 60 m (∵ O is centroid of ∆ABC also)
Let a be the side of ∆ABC

Hence the distance between each other = 40\(\sqrt { 3 } \) m

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.