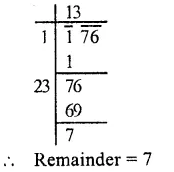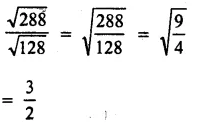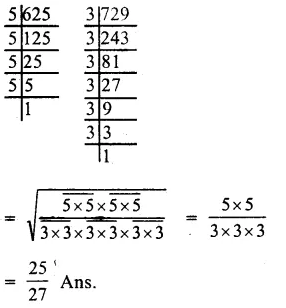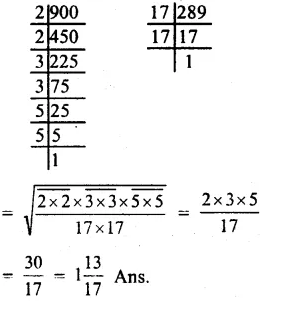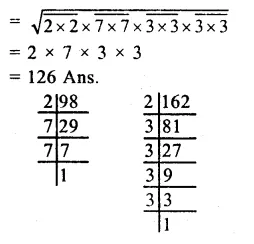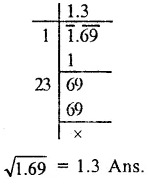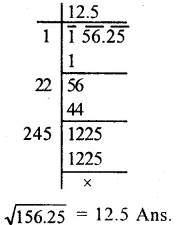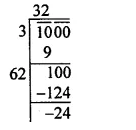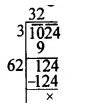Maths Class 8 RS Aggarwal Solutions

RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4A
• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4B
• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4C
• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4D

Question 1.
Solution:
(i) (8)³ = 8 x 8 x 8 = 512
(ii) (15)³ = 15 x 15 x 15 = 3375
(iii) (21)³ = 21 x 21 x 21 = 9261
(iv) (60)³ = 60 x 60 x 60 = 216000 Ans.

Question 2.
Solution:
(i)(1.2)³= 1.2 x 1.2 x 1.2 = 1.728
(ii) (3.5)³ = 3.5 x 3.5 x 3.5 = 42.875
(iii) (0.8)³ = 0.8 x 0.8 x 0.8 = 0.512
(iv) (0.05)³ = 0.05 x 0.05 x 0.05 = 0.000125

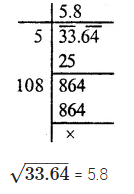
Question 3.
Solution:

Question 4.
Solution:
(i) 125
= \(\overline { 5\times 5\times 5 } ={ \left( 5 \right) }^{ 3 }\)

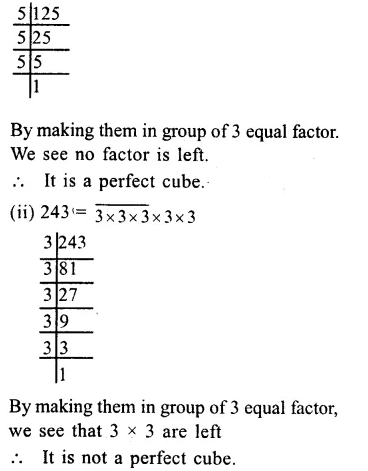
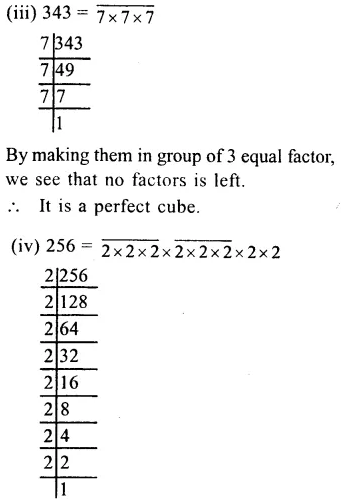
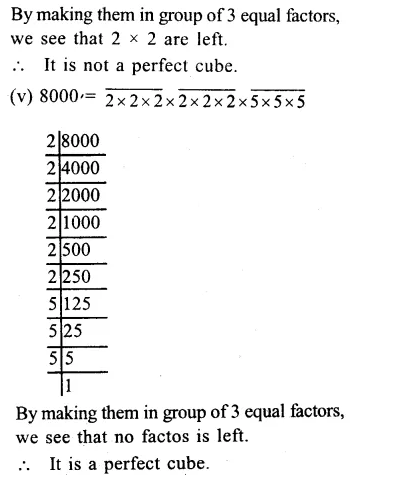
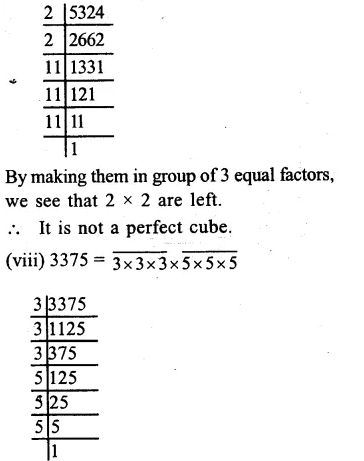
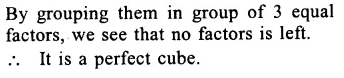
Question 5.
Solution:
We know that cube of an even number is also even.
216, 1000 and 512 are the cubes of even numbers as these are all even numbers. Ans.

Question 6.
Solution:
We know that cube of an odd number is also odd.
125, 343 and 9261 are the cubes of odd natural numbers as these are also odd numbers. Ans.

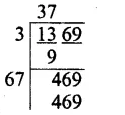
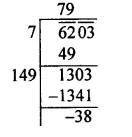
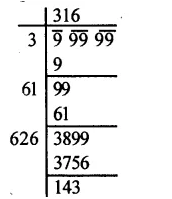
Question 7.
Solution:
Factorising 1323 into prime factors,

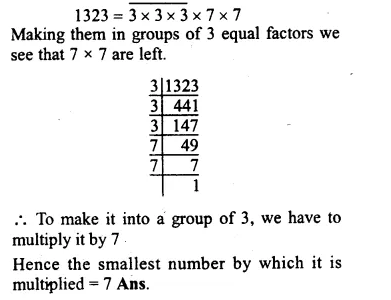
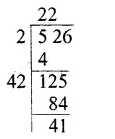
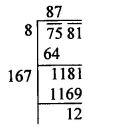
Question 8.
Solution:
Factorising 2560 into prime factors.

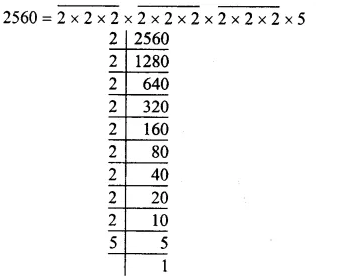
Making them in groups of 3 equal factors, we are left 5
To make it into a group of 3, we have to multiply it by 5 x 5 i.e. by 25.
Hence, the smallest number by which it is multiplied = 25 Ans.

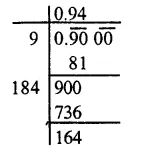
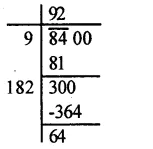
Question 9.
Solution:
Factorising 1600 into prime factors

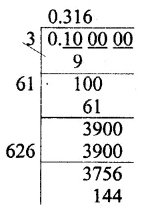
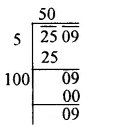
Question 10.
Solution:
Factorising 8788 into prime factors

Making them in groups of 3 equal factors, we are left with 2 x 2
2 x 2 i.e. 4 is to be divided.
Hence least number to be divided for getting perfect cube = 4 Ans.

Hope given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3H

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3A
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3C
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H

Question 1.
Solution:
5478 as it has 8 at in the end (c)

Question 2.
Solution:
2222 as it has 2 in the end (d)

Question 3.
Solution:
1843 as it has 3 in the end (a)

Question 4.
Solution:
4787 as it has 7 in the end (b)

Question 5.
Solution:
81000 as it has an odd number of zeros at its end (c)

Question 6.
Solution:
8, as the number with 8, in the end, cannot be a perfect square. (d)

Question 7.
Solution:
The square of a proper fraction is smaller than the given fraction. (b)

Question 8.
Solution:
1 + 3 + 5 + 7 + … to n terms when n is an odd is equal to n² (c)
Sum of first n odd natural numbers is n²

Question 9.
Solution:
Answer = (d)
(8)² + (15)²
= 64 + 225
= 289 = (17)²

Question 10.
Solution:
Answer = (c)

7 must be subtracted

Question 11.
Solution:
Finding the square root of 526 by division method

We get remainder = 41
Now (22)² = 484 and (23)² = 529
The least number to be added = 529 – 526 = 3 (a)

Question 12.
Solution:
Finding the square root of 15370 by division method
We get remainder = 261
Now (123)² = 15129
and (124)² = 15376
The least number to be added
= 15376 – 15370 = 6 (b)

Question 13.
Solution:
Answer = (d)

Question 14.
Solution:
√0.1 = 0.316 (c)

Question 15.
Solution:
Answer = (b)
\(\sqrt { 0.9\times 1.6 } \)
= \(\sqrt { 1.44 } \)
= \(\sqrt { 1.2\times 1.2 } \)
= 1.2

Question 16.
Solution:
Answer = (c)

Question 17.
Solution:
\(\sqrt { 2\frac { 1 }{ 4 } } \)
= \(\sqrt { \frac { 9 }{ 4 } } =\frac { 3 }{ 2 } \)
= \(1\frac { 1 }{ 2 } \) (b)

Question 18.
Solution:
We know that the square on an even number is also an even number. 196 is the square of an even number (a)

Question 19.
Solution:
We know that the square of an odd number is also an odd number

1369 is an odd number

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3G

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3A
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3C
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H

Evaluate:

Question 1.
Solution:
\(\sqrt { \frac { 16 }{ 81 } } \)
= \(\frac { \sqrt { 16 } }{ \sqrt { 81 } } \)
= \(\sqrt { \frac { 4X4 }{ 9X9 } } \)
= \(\\ \frac { 4 }{ 9 } \)

Worksheets for Class 8 Maths

Question 2.
Solution:
\(\sqrt { \frac { 64 }{ 225 } } \)
= \(\frac { \sqrt { 64 } }{ \sqrt { 225 } } \)
= \(\sqrt { \frac { 8X8 }{ 15X15 } } \)
= \(\\ \frac { 8 }{ 15 } \)

Question 3.
Solution:
\(\sqrt { \frac { 121 }{ 256 } } \)
= \(\frac { \sqrt { 121 } }{ \sqrt { 256 } } \)
= \(\sqrt { \frac { 11X11 }{ 16X16 } } \)
= \(\\ \frac { 11 }{ 16 } \)

Question 4.
Solution:
\(\sqrt { \frac { 625 }{ 729 } } \)

Question 5.
Solution:
\(\sqrt { 3\frac { 13 }{ 36 } } \)
= \(\sqrt { \frac { 3X36+13 }{ 36 } } \)
= \(\sqrt { \frac { 108+13 }{ 36 } } \)
= \(\sqrt { \frac { 121 }{ 36 } } \)
= \(\sqrt { \frac { 11X11 }{ 6X6 } } \)
= \(\\ \frac { 11 }{ 6 } \)

Question 6.
Solution:
\(\sqrt { 4\frac { 73 }{ 324 } } \)
= \(\sqrt { \frac { 4X324+73 }{ 324 } } \)
= \(\sqrt { \frac { 1296+73 }{ 324 } } \)
= \(\sqrt { \frac { 1369 }{ 324 } } \)

Question 7.
Solution:
\(\sqrt { 3\frac { 33 }{ 289 } } \)
= \(\sqrt { \frac { 3X289+33 }{ 289 } } \)
= \(\sqrt { \frac { 867+33 }{ 289 } } \)
= \(\sqrt { \frac { 900 }{ 289 } } \)

Question 8.
Solution:
\(\frac { \sqrt { 80 } }{ \sqrt { 405 } } \)
= \(\sqrt { \frac { 80 }{ 405 } } \)
= \(\sqrt { \frac { 16 }{ 81 } } \)
= \(\frac { \sqrt { 16 } }{ \sqrt { 81 } } \)
= \(\\ \frac { 4 }{ 9 } \)

Question 9.
Solution:
\(\frac { \sqrt { 1183 } }{ \sqrt { 2023 } } \)
= \(\sqrt { \frac { 1183 }{ 2023 } } \)
= \(\sqrt { \frac { 1183\div 7 }{ 2023\div 7 } } \)
= \(\frac { \sqrt { 169 } }{ \sqrt { 289 } } \)
= \(\frac { \sqrt { 13X13 } }{ \sqrt { 17X17 } } \)
= \(\\ \frac { 13 }{ 17 } \)

Question 10.
Solution:
\(\sqrt { 95 } \times \sqrt { 162 } \)
= \(\sqrt { 98\times 162 }\)
= \(\sqrt { 2\times 7\times 7\times 2\times 3\times 3\times 3\times 3 } \)

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3A
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3C
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H

Evaluate:

Question 1.
Solution:

Question 2.
Solution:

\(\sqrt { 33.64 } \) = 5.8

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

\(\sqrt { 10.0489 } \) = 3.17

Question 7.
Solution:

\(\sqrt { 1.0816 } \) = 1.04

Question 8.
Solution:

\(\sqrt { 0.2916 } \) = 0.54

Question 9.
Solution:
\(\sqrt { 3 } \) = 1.73

Question 10.
Solution:
\(\sqrt { 2.8 } \) = 1.6733 = 1.67

Question 11.
Solution:
\(\sqrt { 0.9 } \) = 0.948
= 0.95

Question 12.
Solution:
Length of rectangle (l) = 13.6 m
and width (b) = 3.4 m

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3A
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3C
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H

Evaluate:

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:
Finding the square root of 2509 by division we find that 9 is left as remainder

9 must be subtracted to get the perfect square 100.
Least number to be subtracted = 9

Question 14.
Solution:
Finding the square root of 7581 by division method, we find that 12 is left as remainder.
12 must be subtracted from 7581 to get a perfect square i.e., 7581 – 12 = 7569

(i) The least number to be subtracted = 12
(ii) Perfect square = 7569
(iii) and square root = 87 Ans.

Question 15.
Solution:
Finding the square root of 6203 by division method, we find that 38 is to be added to get a perfect square.
(i) Least number to be added = 38
(ii) Perfect square = 6241
(iii) Square root = 79 Ans.

Question 16.
Solution:
Finding the square root of 8400 by long division method, we find that 64 is to be added to 8400,
We, get 8400 + 64 = 8464

Least number to be added = 64
Perfect square = 8464
Square root = 92 Ans.

Question 17.
Solution:
Least four-digit number = 1000

Finding the square root of 1000 by the division method, we find that 24 must be added to get a perfect square of 4 digits.
Perfect square = 1000 + 24 = 1024 Ans.
square root of 1024 = 32

Question 18.
Solution:
Greatest number of five digits = 99999
Finding the square root of 99999
We get remainder = 143

Required perfect square = 99999 – 143 = 99856
and square root = 316 Ans

Question 19.
Solution:
Area of a square field = 60025 m²
Let its side = a

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.