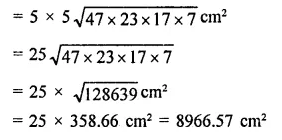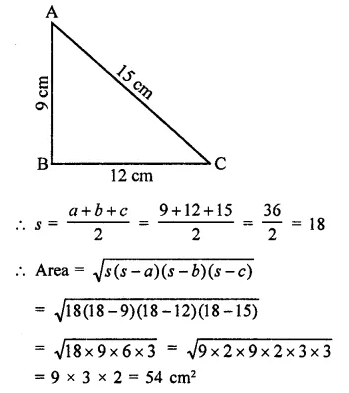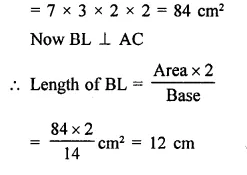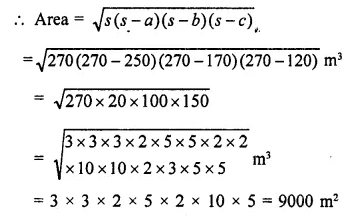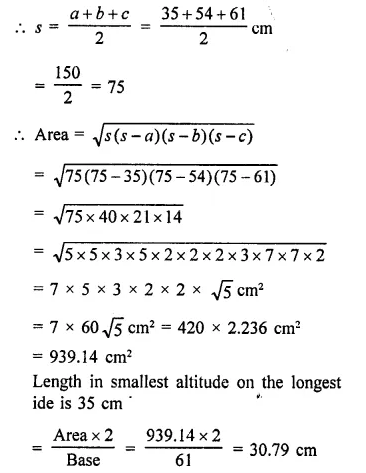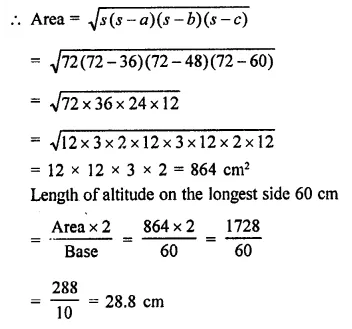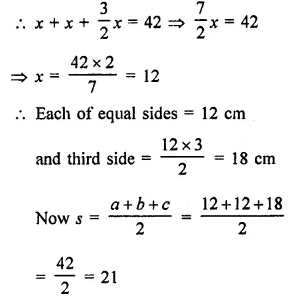Class 9 Maths RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Question 1.
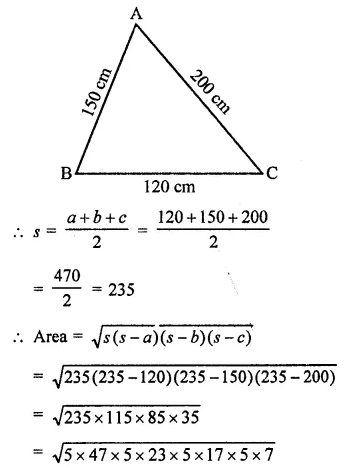
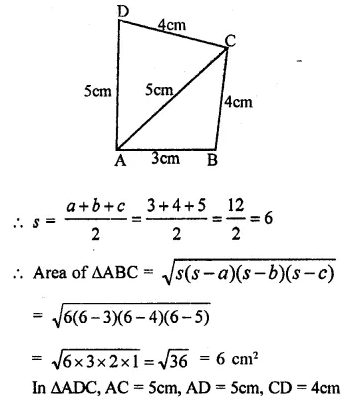
Find the area of a quadrilateral ABCD in which AB = 3cm, BC = 4cm, CD = 4cm, DA = 5cm and AC = 5cm (NCERT)
Solution:
In the quadrilateral, AC is the diagonal which divides the figure into two triangles
Now in ∆ABC, AB = 3 cm, BC = 4cm, AC = 5cm

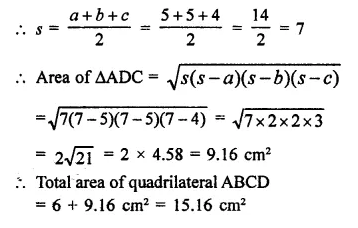
Question 2.
The sides of a quadrangular field taken in order are 26 m, 27 m, 7 m and 24 m respectively. The angle contained by the last two sides is a right angle. Find its area.
Solution:
In quad. ABCD, AB = 26 m, BC = 27 m CD = 7m, DA = 24 m, ∠CDA = 90°
Join AC,

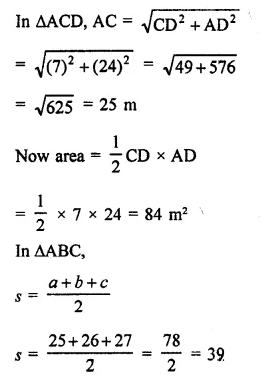
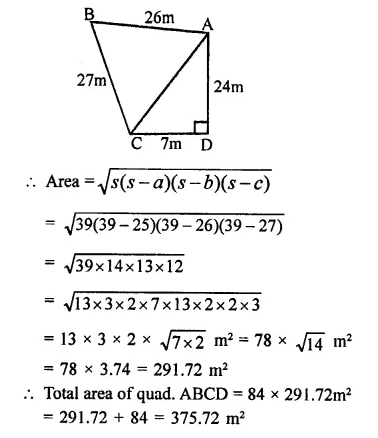
Question 3.
The sides of a quadrilateral taken in order are 5, 12, 14 and 15 metres respectively, and the angle contained by the first two sides is a right angle. Find its area.
Solution:
In quad. ABCD,
AB = 5m, BC = 12 m, CD = 14m,
DA = 15 m and ∠ABC = 90°
Join AC,
Now in right ∆ABC,
AC² = AB² + BC² = (5)² + (12)²
= 25 + 144 = 169 = (13)²
∴ AC = 13 m
Now area of right ∆ABC

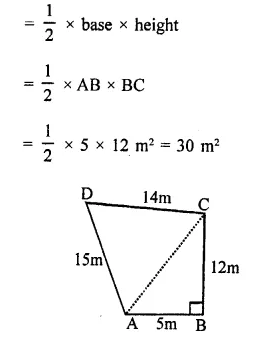
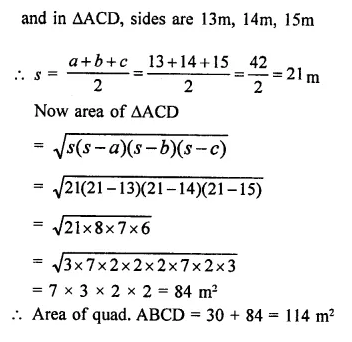
Question 4.
A park, in shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9m, BC = 12m, CD = 5m and AD = 8m. How much area does it occupy? (NCERT)
Solution:
In quadrilateral ABCD,
AB = 9m, BC = 12m, CD = 5m and
DA = 8m, ∠C = 90°
Join BD,
Now in right ∆BCD,
BD² = BC²+ CD² = (12)² + (5)²
= 144 + 25 = 169 = (13)²
∴ BD = 13m

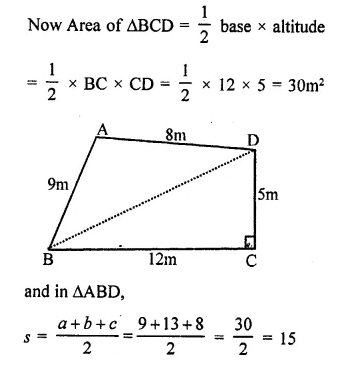
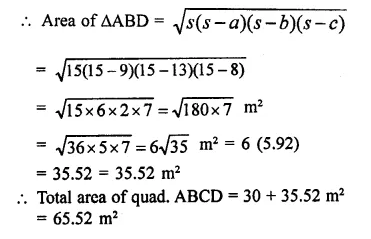
Question 5.
Find the area of a rhombus whose perimeter is 80m and one of whose diagonal is 24m.
Solution:
Perimeter of rhombus ABCD = 80 m

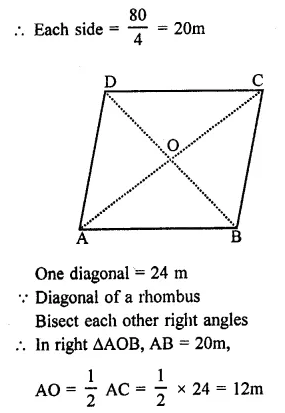
Question 6.
A rhombus sheet whose perimeter = 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of ₹5 per m². Find the cost of painting.
Solution:
Perimeter of the rhombus shaped sheet = 32 m

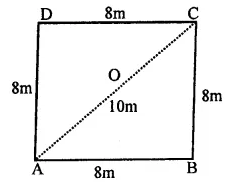
∴ Length of each side = \(\frac { 32 }{ 4 }\) = 8m
and length of one diagonal AC = 10 m
In ∆ABC, sides are 8m, 8m, 10m

Question 7.
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take \(\sqrt { 3 } \) = 1.73 )
Solution:
In quadrilateral ABCD, AD = 24cm, ∠BAD = 90°

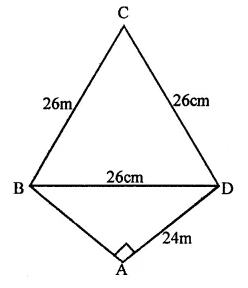
BCD is an equilateral triangle with side 26cm
In right ∆ABD,
BD² = AB²+ AD²
(26)² = AB² + (24)²
⇒ 676 = AB² + 576
AB² = 676 – 576 = 100 = (10)²
∴ AB = 10cm
Now area of right ∆ABD,

Question 8.
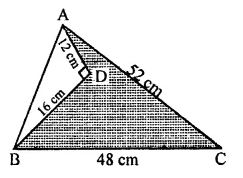
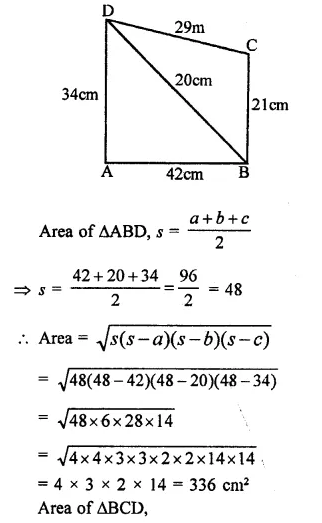
Find the area of a quadrilateral ABCD in which AB = 42cm, BC = 21cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
Solution:
In quadrilateral ABCD,
AB = 42 cm, BC = 21 cm, CD = 29cm DA = 34 cm, BD = 20 cm

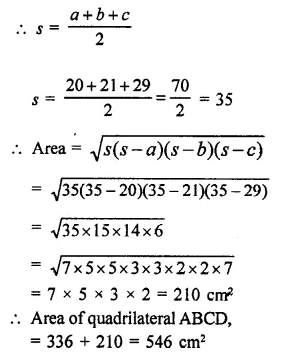
Question 9.
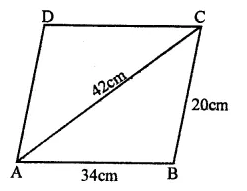
The adjacent sides of a parallelogram ABCD measures 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Solution:
In ||gm ABCD,
AB = 34cm, BC = 20 cm
and AC = 42 cm

∵ The diagonal of a parallelogram divides into two triangles equal in area,
Now area of ∆ABC,

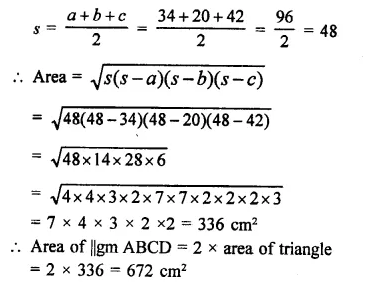
Question 10.
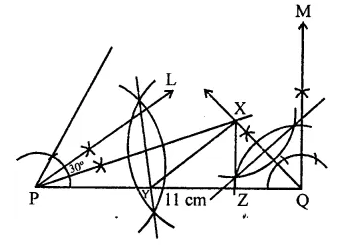
Find the area of the blades of the magnetic compass shown in figure. (Take \(\sqrt { 11 } \) = 3.32).

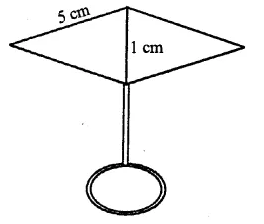
Solution:
ABCD is a rhombus with each side 5cm and one diagonal 1cm
Diagonal BD divides into two equal triangles Now area of ∆ABD,

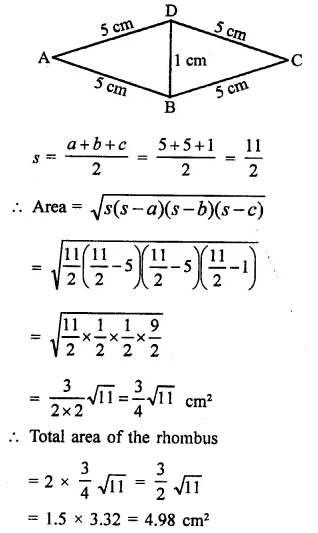
Question 11.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.
Solution:
Area of a triangle with same base and area of a 11gm with equal sides of triangle are 13, 14, 15 cm

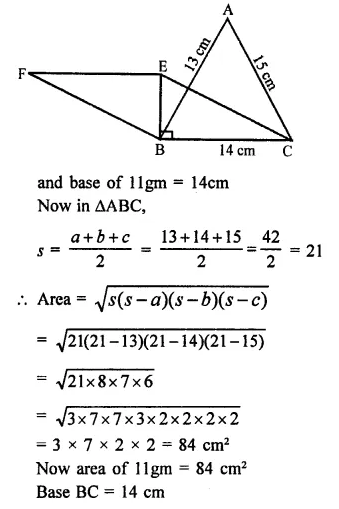
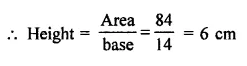
Question 12.
Two parallel sides of a trapezium are 60cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Solution:
In trapezium ABCD, AB || DC

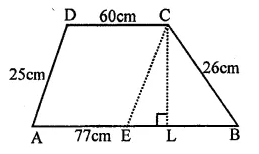
AB = 77cm, BC = 26 cm, CD 60cm DA = 25 cm
Through, C, draw CE || DA meeting AB at E
∴ AE = CD = 60 cm and EB = 77 – 60 = 17 cm,
CE = DA = 25 cm
Now area of ∆BCE, with sides 17 cm, 26 cm, 25 cm

Question 13.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9cm, CD = 12cm, ∠ACB = 90° and AC = 15cm.
Solution:
In right ΔABC, ∠ACB = 90°
AB² = AC² + BC²
(17)² = (15)²+ BC² = 289 = 225 + BC²

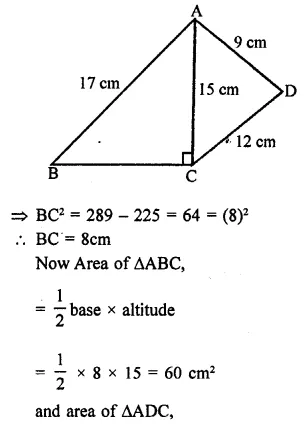
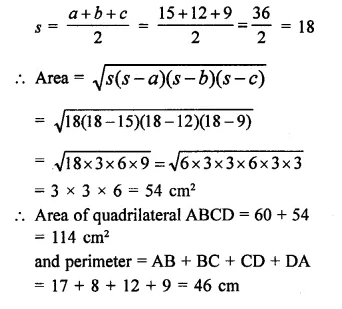
Question 14.
A hand fan is made by stitching 10 equal size triangular strips of two different types of paper as shown figure. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each types of paper needed to make the hand fan.
Solution:
In the figure, a hand fan has 5 isosceles and triangle. With sides 25 cm, 25 cm and 14 cm each.

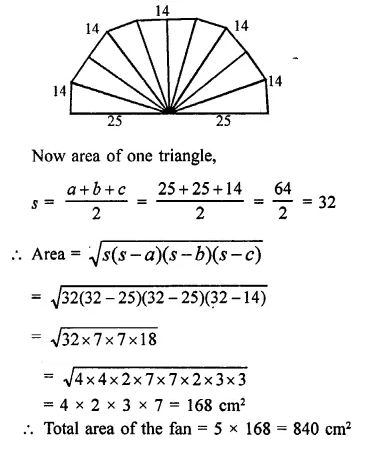
Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Question 1.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm.
Solution:
Sides of triangle are 120 cm, 150 cm, 200 cm

Question 2.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm.
Solution:
Sides of a triangle are 9 cpi, 12 cm, 15 cm

Question 3.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Perimeter of a triangle = 42 cm
Two sides are 18 cm and 10 cm
Third side = 42 – (18 + 10)
= 42 – 28 = 14 cm

Question 4.
In a ∆ABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ∆ABC and hence its altitude on AC.
Solution:
Sides of triangle ABC are AB = 15 cm, BC = 13 cm, AC = 14 cm

Question 5.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 540 m
Ratio in sides = 25 : 17 : 12
Sum of ratios = 25 + 17 + 12 = 54

Question 6.
The perimeter of a triangle is 300 m. If its sides are in the ratio 3:5:7. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 300 m
Ratio in the sides = 3 : 5 : 7
∴ Sum of ratios = 3 + 5 + 7= 15

Question 7.
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution:
Perimeter of a triangular field = 240 dm
Two sides are 78 dm and 50 dm
∴ Third side = 240 – (78 + 50)
= 240 – 128 = 112 dm

Question 8.
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes.
Solution:
Sides of a triangle are 35 cm, 54 cm, 61 cm

Question 9.
The lengths of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Solution:
Ratio in the sides of a triangle = 3:4:5

Question 10.
The perimeter of an isosceles triangle is 42 cm and its base is (3/2) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Solution:
Perimeter of an isosceles triangle = 42 cm
Base = \(\frac { 3 }{ 2 }\) of its one of equal sides
Let each equal side = x, then 3
Base = \(\frac { 3 }{ 2 }\) x

Question 11.
Find the area of the shaded region in figure.

Solution:
In ∆ABC, AC = 52 cm, BC = 48 cm
and in right ∆ADC, ∠D = 90°
AD = 12 cm, BD = 16 cm
∴ AB²=AD² + BD² (Pythagoras Theorem)
(12)² + (16)² = 144 + 256 = 400 = (20)²
∴ AB = 20 cm

Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Construct a ∆ABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B = 60°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 4.8 cm.
(iii) Join EC.
(iv) Draw perpendicular bisector of CE which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 2.
Construct a ∆ABC in which AB + AC = 5.6 cm, BC = 4.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.5 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 5.6 cm and join CE.
(iii) Draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 3.
Construct a AABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.4 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 1.5 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of CE which intersects BE produced at A.
(v) Join AC.
∆ABC is the required triangle.

Question 4.
Using ruler and compasses only, construct a ∆ABC, given base BC = 7 cm, ∠ABC = 60° and AB + AC = 12 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 7 cm!
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 12 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of EC which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 5.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 10 cm.
(ii) At P, draw a ray PX making an angle of 90° and at Q, QY making an angle of 60°.
(iii) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of AP and AQ intersecting PQ at B and C respectively,
(v) Join AB and AC.
∆ABC is the required triangle.

Question 6.
Construct a triangle ABC such that BC = 6cm, AB = 6 cm and median AD = 4 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm and bisect it at D.
(ii) With centre B and radius 6 cm and with centre D and radius 4 cm, draw arcs intersecting each other at A.
(iii) Join AD and AB and AC.
Then ∆ABC is the required triangle.

Question 7.
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm

(ii) At B, draw a ray BX making an angle of 90° and cut off BE = 10 cm.
(iii) Join EC and draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 8.
Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 6.4 cm.
(ii) At P draw a ray PX making an angle of 60° and at Q, a ray QY making an angle of 45°.
(iii) Draw the bisector of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of PA and QA intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 9.
Using ruler and compasses only, construct a ∆ABC, from the following data:
AB + BC + CA = 12 cm, ∠B = 45° and ∠C = 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 12 cm.
(ii) Draw ray PX at P making are angle of 45° and at Q, QY making an angle of 60°.
(Hi) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(v) Draw the perpendicular bisector of AP and AQ intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 10.
Construct a triangle XYZ in which ∠Y = 30° , ∠Z = 90° XY +YZ + ZX = 11
Solution:
Steps of construction :
(i) Draw a line segment PQ =11 cm.
(ii) At P, draw a ray PL making an angle of 30° and Q, draw another ray QM making an angle of 90°.
(iii) Draw the angle bisector of ∠P and ∠Q intersecting each other at X.
(iv) Draw the perpendicular bisector of XP and XQ. Which intersect PQ at Y and Z respectively.
(v) Join XY and XZ.
Then ∆XYZ is the required triangle

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Solution:
Steps of construction :
(i) Draw an angle BAC.
(ii) Draw a line DF.
(iii) With centre A and D, draw arcs of equal radius which intersect AC at L and AB at M and DF at P.
(iv) Cut off PQ = LM and join DQ and produce it to E, then
∠EDF = ∠BAC.

Question 2.
Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Solution:
Steps of construction :
(i) Draw an angle ABC which is an obtuse i.e. more than 90°.
(ii) With centre B and a suitable radius draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
ThenBD is die bisector of ∠ABC.
On measuring each part, we find each angle = 53°.

Question 3.
Using your protractor, draw an angle of measure 108°. With this angle as given, draw an angle of 54°.
Solution:
Steps of construction :
(i) With the help of protractor draw an angle ABC = 108°.
As 54° = \(\frac { 1 }{ 2 }\) x 108°
∴ We shall bisect it.

(ii) With centre B and a suitable radius, draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF, draw arcs intersecting each other at G
(iv) Join BG and produce it to D.
Then ∠DBC = 54°.

Question 4.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Solution:
Steps of construction :
(i) Using protractor, draw a right angle ∆ABC.
i. e. ∠ABC = 90°.
(ii) With centre B and a suitable radius, draw an arc which meets BC at E and BA at F.
(iii) With centre E and F, draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC =\(\frac { 1 }{ 2 }\) x 90° = 45°.

Question 5.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution:
Steps of construction :
(i) Draw a linear pair ∠DCA and ∠DCB.
(ii) Draw the bisectors of ∠DCA and ∠DCB. Forming ∠ECF on measuring we get ∠ECF = 90°.
Verification : ∵∠DCA + ∠DCB = 180°
⇒ \(\frac { 1 }{ 2 }\) ∠DCA + \(\frac { 1 }{ 2 }\) ∠DCB = 180° x \(\frac { 1 }{ 2 }\) = 90°
∴ ∠ECF = 90°
i.e. EC and FC are perpendicular to each other.

Question 6.
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line
Solution:
Steps of construction :
(i) Draw two lines AB and CD intersecting each other at O.
(ii) Draw the bisector of ∠AOD and also the bisector of ∠BOC. Which are OP and OQ respectively. We see that OP and OQ are in the same straight line.

Question 7.
Using ruler and compasses only, draw a right angle.
Solution:
Steps of construction :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius, draw an arc meeting BC at E.
(iii) With centre E and same radius, cut off arcs EF and FG.
(iv) Bisect arc FG at H.
(v) Join BH and produce it to A.
Then ∠ABC = 90°.

Question 8.
Using ruler and compasses only, draw an angle of measure 135°.
Solution:
Steps of construction :
(i) Draw a line DC and take a point B on it.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P, cut off arcs PQ, QR and RS.
(iv) Bisect as QR at T and join BT and produce it to E.
(v) Now bisect the arc KS at RL.
(vi) Join BL and produce it to A.
Now ∠ABC = 135°.

Question 9.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Solution:
Steps of construction :
(i) Draw an angle ABC = 12° with the help of protractor.
(ii) With centre B and a suitable radius, draw an arc EF.
(iii) With centre E and F, draw arcs intersecting
each other at G and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC = 72° x \(\frac { 1 }{ 2 }\) = 36°.
(iv) Again bisect ∠ABD in the same way then PB is the bisector of ∠ABD.
∴ ∠PBC = 36° + \(\frac { 1 }{ 2 }\) x 36°
= 36° + 18° = 54°
Hence ∠PBC = 54°

Question 10.
Construct the following angles at the initial point of a given ray and justify the construction:
(i) 45°
(ii) 90°
Solution:
(i) 45°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) With centre E, cut off equal arcs EF and FG.
(d) Bisect FG at H.
(e) Join BH and produce to X so that ∠XBC = 90°.
(f) Bisect ∠XBC so that ∠ABC = 45°.

(ii) 90°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E and with centre E cut off arcs from E, EF = FG
(c) Now bisect the arc EG at H.
(d) Join BH and produce it to A.
∴ ∠ABC = 90°.

Question 11.
Construct the angles of the following measurements:
(i) 30°
(ii) 75°
(iii) 105°
(iv) 135°
(v) 15°
(vi) 22 \(\frac { 1 }{ 2 }\)°
Solution:
(i) 30°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) Cut off arcs EF and bisect it at G.
So that ∠ABC = 30°.

(ii) 75°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF = FG from E.
(d) Bisect the arc FG at K and join BK so that ∠KBC = 90°.
(e) Now bisect arc HF at L and join BL and produce it to A so that ∠ABC = 75°.

(iii) 105°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) From E, cut off arc EF = FG and divide FG at H.
(d) Join BH meeting the arc at K.
(e) Now bisect the arc KG at L.
Join BL and produce it to A.
Then ∠ABC = 105°.

(iv) 135°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) From E, cut off EF = FG = GH.
(d) Bisect arc FG at K, and join them.
(e) Bisect arc KH at L.
(f) Join BL and produce it to A, then ∠ABC = 135°.

(v) 15°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF from E and bisect it at G. Then ∠GBC = 30°.
(d) Again bisect the arc EJ at H.
(e) Join BH and produce it to A.
Then ∠ABC = 15°.

(vi) 22 \(\frac { 1 }{ 2 }\)°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc and from E, cut off EF = FG
(c) Bisect FG at H so that ∠HBC = 90°.
(d) Now bisect ∠HBC at K. So that ∠YBC = 45°.
(e) Again bisect ∠YBC at J. So thttt ∠ABC = 22 \(\frac { 1 }{ 2 }\)°

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Draw a line segment of length 8.6 cm. Bisect it and measure the length of each part.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8.6 cm.
(ii) With centres A and B, and radius more than half of AB, draw arcs which intersect each other at E and F, on both sides of AB.
(iii) Join EF which intersects AB at D.
D is the required mid point of AB.
Measuring each part, it is 4.3 cm long.

Question 2.
Draw a line segment AB of length 5.8 cm. Draw the perpendicular bisector of this line segment.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5.8 cm.
(ii) With centres A and B and radius more than half of AB, draw arcs intersecting each other at E and F.
(iii) Join EF which is the required perpendicular bisector of AB.

Question 3.
Draw a circle with centre at point O and radius 5 cm. Draw its chord AB, draw the perpendicular bisector of line segment AB. Does it pass through the centre of the circle?
Solution:
Steps of construction :
(i) Draw a circle with centre O and radius 5 cm.
(ii) Draw a chord AB of the circle.
(iii) With centres A and B and radius more than half of AB draw arcs intersecting each other at P and Q.
(iv) Join PQ which intersects AB at D and passes through O, the centre of the circle.

Question 4.
Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not parallel to CD. Draw the perpendicular bisectors of AB and CD. At what point do they intersect?
Solution:
Steps of construction :
(i) Draw a circle with centre O and a suitable radius.
(ii) Draw two chords AB and CD which are not parallel to each other.
(iii) Draw the perpendicular bisectors of AB and CD with the help of ruler and compasses. We see that these two chords intersect each other at the centre O, of the circle.

Question 5.
Draw a line segment of length 10 cm and bisect it. Further bisect one of the equal parts and measure its length.
Solution:
Steps of construction :
(i) Draw a line segment AB = 10 cm.
(ii) With the help of ruler and compasses, bisect AB at C.
(iii) Bisect again AC at D.
Measuring AD, it is 2.5 cm long.

Question 6.
Draw a line segment AB and bisect it. Bisect one of the equal parts to obtain a line segment of length \(\frac { 1 }{ 2 }\) (AB).
Solution:
Steps of construction :
(i) Draw a line segment AB.
(ii) With the help of ruler and compasses, draw the bisector of AB which bisects AB at C.
(iii) Similarly, in the same way draw the bisector of AC at D.
We see that AC = \(\frac { 1 }{ 2 }\) (AB).

Question 7.
Draw a line segment AB and by ruler and compasses, obtain a line segment of length \(\frac { 3 }{ 4 }\) (AB).
Solution:
Steps of construction :
(i) Draw a line segment AB.
(ii) Draw a ray AX making an acute angle with A3 and equal 4 parts at A₁, A₂, A₃ and A₄.
(iii) JoinA₄B.
(iv) From A3, draw a line parallel to A₄B which meets AB at C.
C is the required point and AC = \(\frac { 3 }{ 4 }\) (AB).

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.