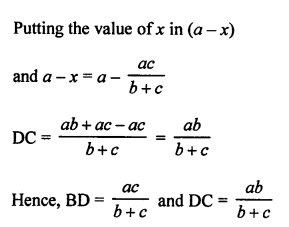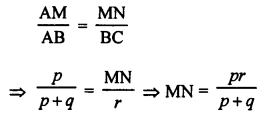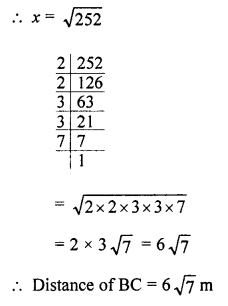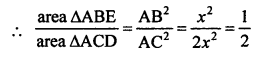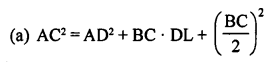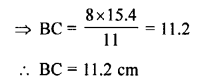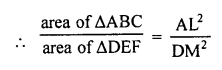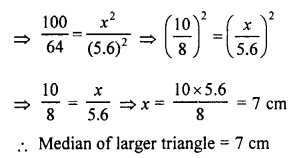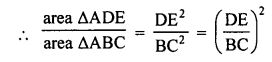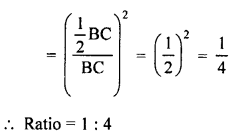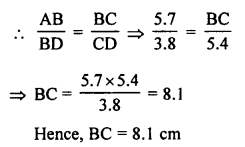Class 10 Maths RS Aggarwal Solutions

RS Aggarwal Class 10 Solutions Chapter 4 Triangles MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
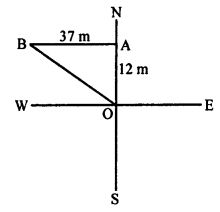
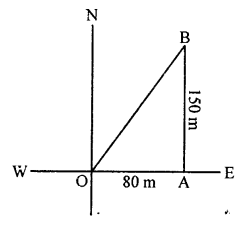
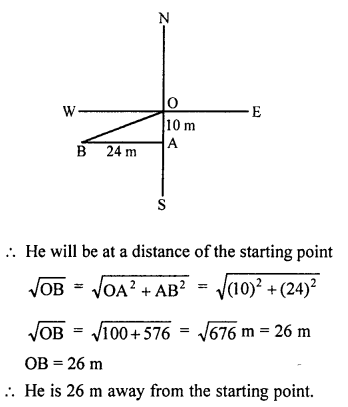
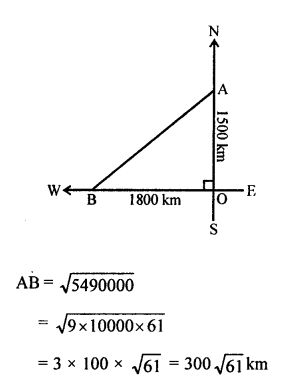
(c) A man goes from O to 24 m due west at A and then 10 m due north at B.

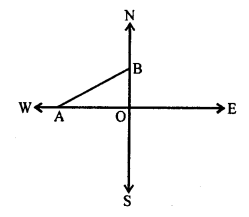
Now, AB² = OA² + OB²
= (24)² + (10)² = 576 + 100 = 676 = (26)²
AB = 26 m

Question 2.
Solution:
(b) Two poles AB and CD are standing on the plane ground 8 m apart.
AB = 13 m and CD = 7 m, CE || DB

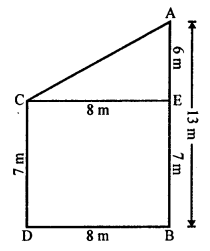
In right ∆ACE,
AC² = CE² + AE²
= (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 m
Distance between the tops of poles = 10 m

Question 3.
Solution:
(c) A vertical stick AB = 1.8 m
and its shadow = 45 cm = 0.45 m

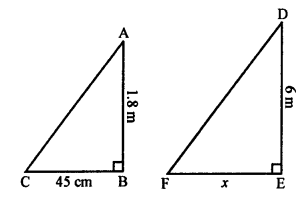
At the same time, let x cm be the shadow of 6 m long pole.
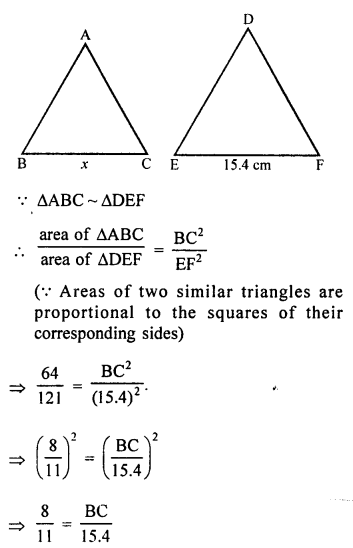
∆ABC ~ ∆DEF

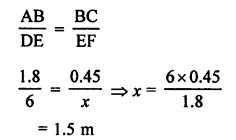
Question 4.
Solution:
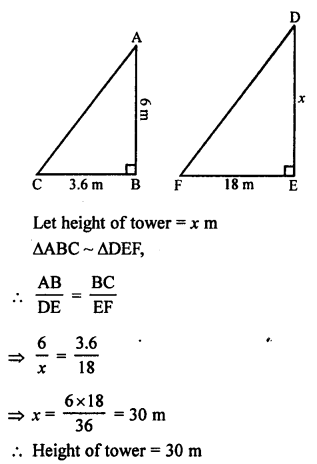
(d) Shadow of a vertical pole 6 m long is 3.6 m on the ground and shadow of a tower at the same, is 18 m.

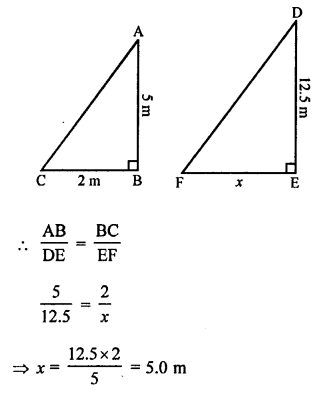
Question 5.
Solution:
(d) Shadow of 5 m long stick = 2 m
Let shadow of 12.5 m high tree at the same time = x
∆ABC ~ ∆DEF

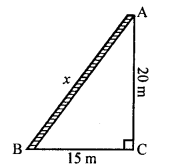
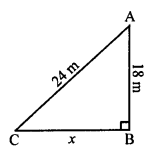
Question 6.
Solution:
(a) Length of ladder AB = 25 m .
Height above the ground = 24 m

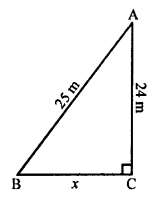
Let its foot is x m away from the foot of building.
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(25)² = (24)² + x²
⇒ 625 = 576 + x²
⇒ x² = 625 – 576 = 49 = (7)²
x = 7
Distance = 7 m

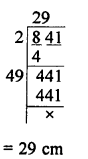
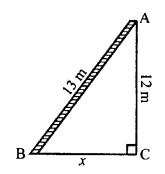
Question 7.
Solution:
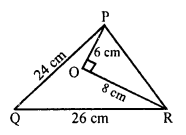
(b) O is a point inside ∆MNP such that
MOP = 90°, OM = 16 cm, OP = 12 cm.
If MN = 21 cm ∠NMP = 90°, then NP = ?
Let MP = x Now, in right ∆MOP,
∠O = 90°
MP² = OM² + OP² (Pythagoras Theorem)
= (16)² + (12)² = 256 + 144 = 400 = (20)²
MP = 20 cm
Now, in right ∆MNP, ∠M = 90°
NP² = MN² + MP²
= (21)² + (20)² = 441 + 400 = 841 = (29)²
NP = 29 cm

Question 8.
Solution:
(b) Let ∆ABC is a right angled triangle with ∠B = 90°
AC = 25 cm
Let one side AB of the other two sides = x cm
then second side BC = (x + 5) cm
According to the Pythagoras Theorem,
AC² = AB² + BC²
(25)² = x² + (x + 5)²
625 = x² + x² + 10x + 25
⇒ 2x² + 10x + 25 – 625 = 0
⇒ 2x² + 10x – 600 = 0
⇒ x² + 5x – 300 = 0
⇒ x² + 20x – 15x – 300 = 0
⇒ x (x + 20) – 15 (x + 20) = 0
⇒ (x + 20)(x – 15) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative,
or x – 15 = 0, then x = 15
First side = 15 cm
and second side = 15 + 5 = 20 cm

Question 9.
Solution:
(b) Side of an equilateral triangle = 12 cm

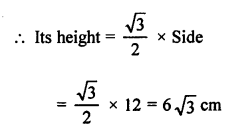
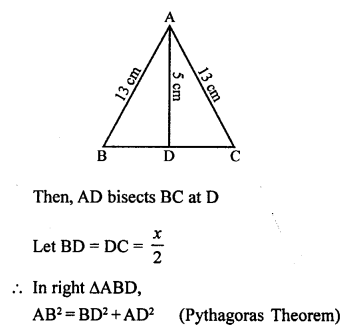
Question 10.
Solution:
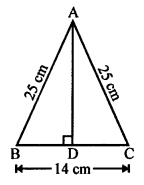
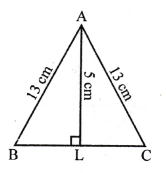
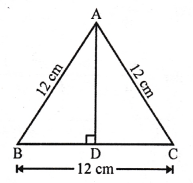
(d) In isosceles ∆ABC,
AB = AC = 13 cm
Length of altitude AB, (from A to BC) = 5 cm

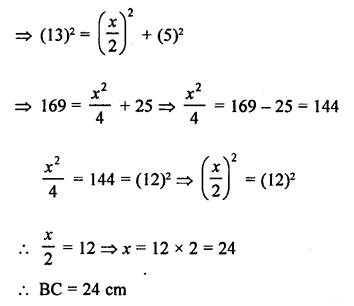
Question 11.
Solution:
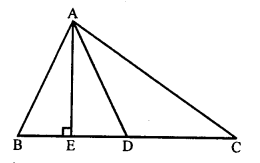
(a) In the given figure,
AB = 6 cm, AC = 8 cm
AD is the bisector of ∠A which meets BC at D.

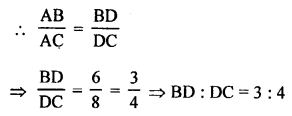
Question 12.
Solution:
(d) In the given figure,
AD is the internal bisector of ∠A
BD = 4 cm, DC = 5 cm, AB = 6 cm
Let AC = x cm

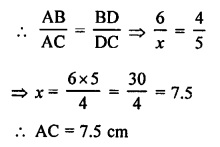
Question 13.
Solution:
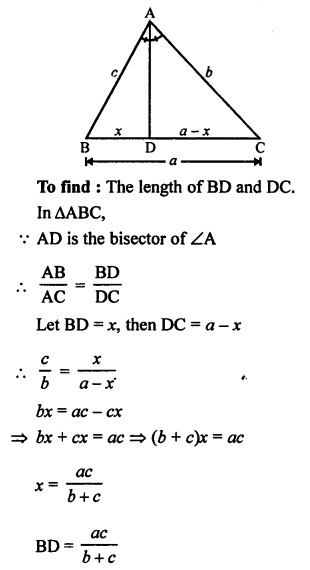
(b) In the given figure,
AD is the bisector of ∠A of ∆ABC.
AB = 10 cm, AC = 14 cm and BC = 6 cm
Let CD = x cm
Then BD = (6 – x) cm
Now, AD is the bisector of ∠A

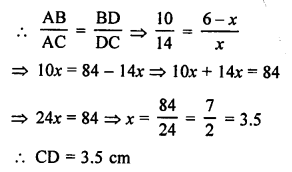
Question 14.
Solution:
(b) In a ∆ABC, AD ⊥ BC and BD = DC

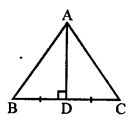
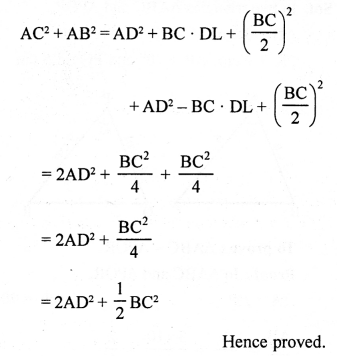
In a ∆ABC, AD = \(\frac { 1 }{ 2 }\) BC and BD = DC.
In right ∆ABD and ∆ACD
AD = AD (common)
∠ABD = ∠ADC (each 90°)
BD = DC (given)
∆ABD = ∆ACD (SAS axiom)
AB = AC
∆ABC is an isosceles triangle.

Question 15.
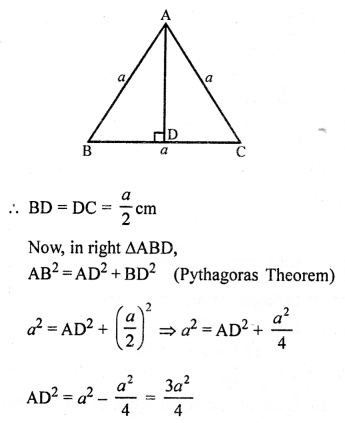
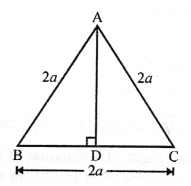
Solution:
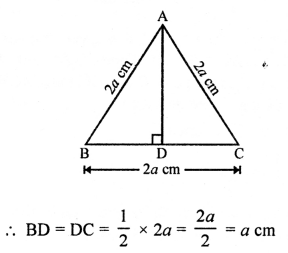
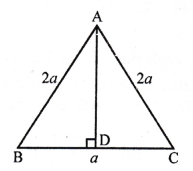
(c) In equilateral ∆ABC, AD ⊥ BC
Then BD = DC = \(\frac { 1 }{ 2 }\) BC
Now, in right ∆ABD,
AB² = BD² + AD² (Pythagoras Theorem)

Question 16.
Solution:
(c) In a rhombus, each side = 10 cm and one diagonal = 12 cm
AB = BC = CD = DA = 10 cm BD = 12 cm

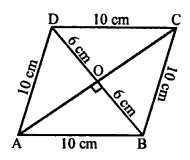
The diagonals of a rhombus bisect each other at right angles.
In ∆AOB,
AB² = AO² + BO²
⇒ (10)² = AO² + (6)²
⇒ AO² = (10)² – (6)² = 100 – 36 = 64 = 8²
AO = 8 cm
Diagonals AC = 2 x AO = 2 x 8 = 16 cm

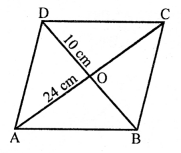
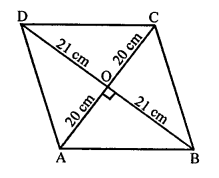
Question 17.
Solution:
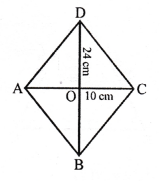
(b) Length of diagonals of a rhombus are 24 cm and 10 cm.
The diagonals of a rhombus bisect each other at right angles.

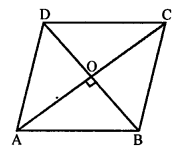
In rhombus ABCD
AO = OC, BO = OD
Let AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 18.
Solution:
(b) Diagonals of e. quadrilateral divides each other proportionally, then it is

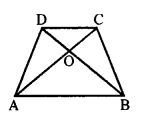
In quadrilateral ABCD, diagonals AC and BD intersect each-other at O and \(\frac { AO }{ OC }\) = \(\frac { BO }{ OD }\)
Then, quadrilateral ABCD is a trapezium.

Question 19.
Solution:
(a) In the given figure,
ABCD is a trape∠ium and its diagonals AC
and BD intersect at O.
and OA = (3x – 1) cm OB = (2x + 1) cm, OC and OD = (6x – 5) cm

Question 20.
Solution:
(a) The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram

Question 21.
Solution:
(c) If the bisector of angle of a triangle bisects the opposite side of a triangle.

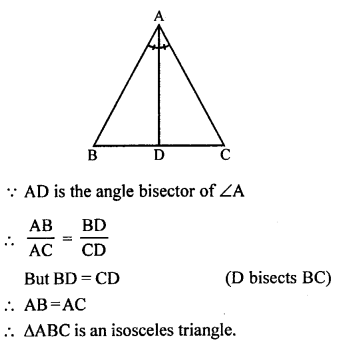
Question 22.
Solution:
(a) In ∆ABC,

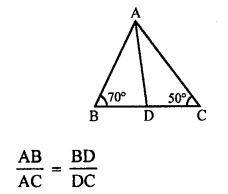
∠B = 70° and ∠C = 50°
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
∠A = 180° – (∠B + ∠C)
= 180° – (70° + 50°)
= 180° – 120° = 60°
\(\frac { AB }{ AC }\) = \(\frac { BD }{ DC }\)
AD is the bisector of ∠A
∠BAD = \(\frac { 60 }{ 2 }\) = 30°

Question 23.
Solution:
(b) In ∆ABC, DE || BC
AD = 2.4 cm, AE = 3.2 cm, EC = 4.8 cm
Let AD = x cm
DE || BC

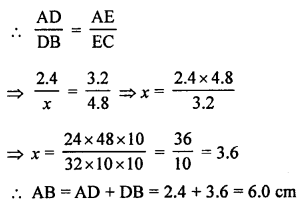
Question 24.
Solution:
(b) In ∆ABC, DE || BC
AB = 7.2 cm, AC = 6.4 cm, AD = 4.5 cm
Let AE = x cm
DE || BC
∆ADE ~ ∆ABC

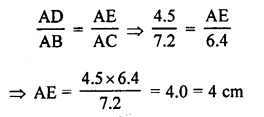
Question 25.
Solution:
(c) In ∆ABC, DE || BC
AD = (7x – 4) cm, AE = (5x – 2) cm DB = (3x + 4) cm and EC = 3x cm
In ∆ABC, DE || BC

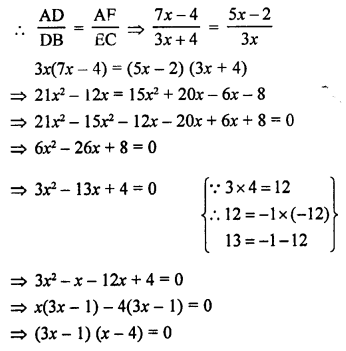
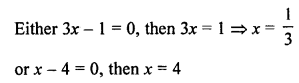
Question 26.
Solution:
(d) In ∆ABC, DE || BC

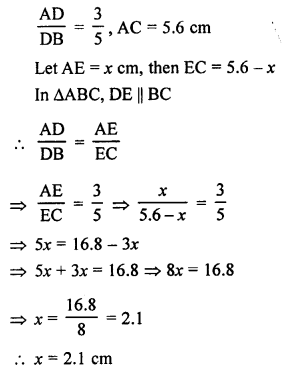
Question 27.
Solution:
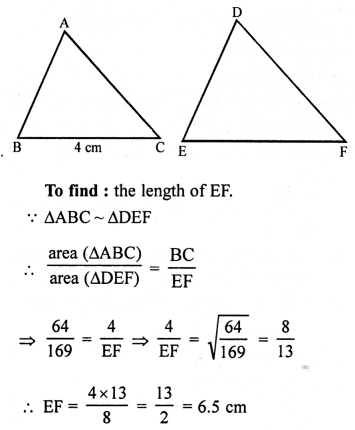
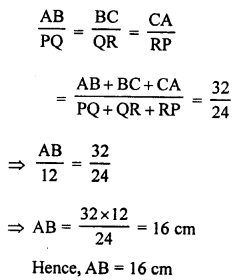
(b) ∆ABC ~ ∆DEF

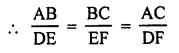
Question 28.
Solution:
(a) ∆ABC ~ ∆DEF

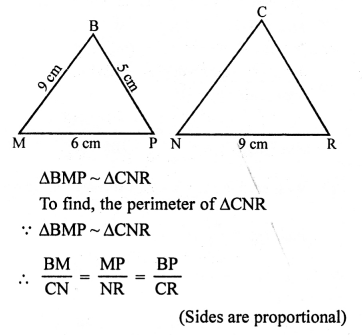
Question 29.
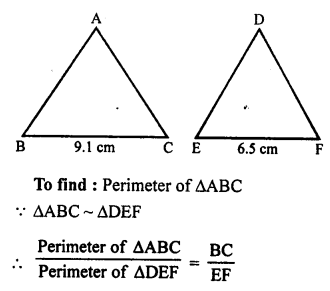
Solution:
(d) ∆DEF ~ ∆ABC

Perimeter of ∆DEF = DE + EF + DF
= 12 + 8 + 10 = 30 cm

Question 30.
Solution:
(d) ABC and BDE are two equilateral triangles such that D is the midpoint of BC.

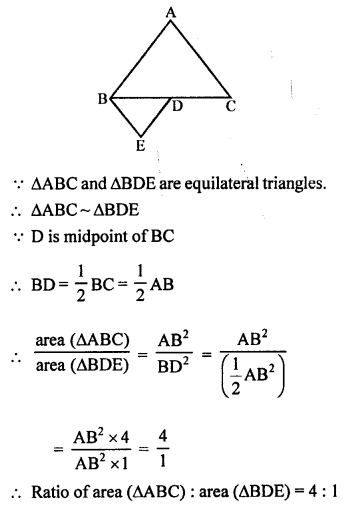
Question 31.
Solution:
(b) ∆ABC ~ ∆DFE.
∠A = 30°, ∠C = 50°, AB = 5cm, AC = 8 cm and DF = 7.5 cm

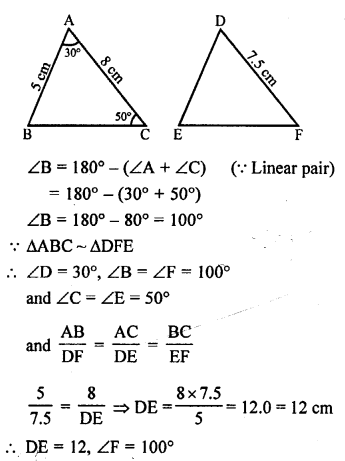
Question 32.
Solution:
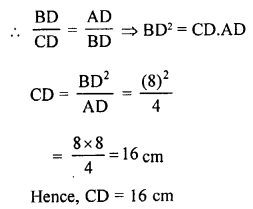
(c) In ∆ABC, ∠A = 90°
AD ⊥ BC
In ∆ABD and ∆ADC

Question 33.
Solution:
(c) In ∆ABC, AB = 6 cm, AC = 12 cm and BC = 6 cm.

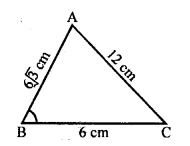
Longest side (AC)2 = (12)2 = 144
AB2 + BC2 = (6√3)2 + (6)2 = 108 + 36 = 144
AC2 = AB2 + BC2 (Converse of Pythagoras Theorem)
∠B = 90°

Question 34.
Solution:
(c) In ∆ABC and ∆DEF, \(\frac { AB }{ DE }\) = \(\frac { BC }{ FD }\)

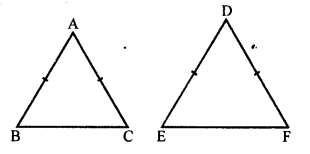
For similarity,
Here, included angles must be equal and these
are ∠B = ∠D.

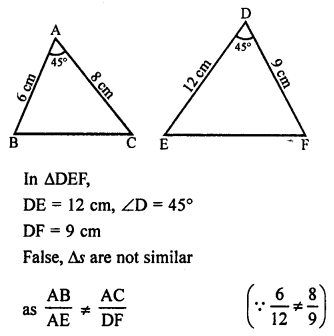
Question 35.
Solution:
(b) In ∆DEF and ∆PQR,
∠D = ∠Q and ∠R = ∠E

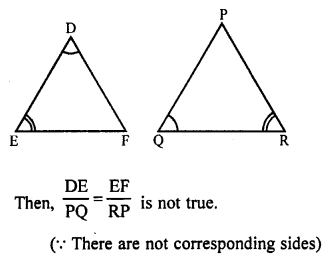
Question 36.
Solution:
(c) ∆ABC ~ ∆EDF
∠A = ∠E, ∠B = ∠D, ∠C = ∠F

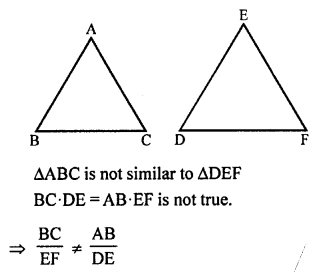
Question 37.
Solution:
(b) In ∆ABC and ∆DEF,
∠B = ∠E, ∠F = ∠C and AB = 3DE
The triangles are similar as two angles are equal but including sides are not proportional.

Question 38.
Solution:
(a)

Question 39.
Solution:
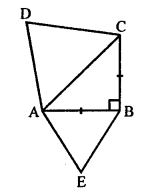
(d) In the given figure, two line segments AC and BD intersect each other at P such that
PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°
In ∆ABP and ∆CPD,

Question 40.
Solution:
(d) Corresponding sides of two similar triangles = 4:9
The areas of there triangle will be in the ratio

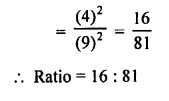
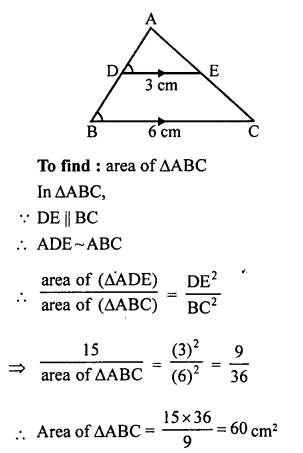
Question 41.
Solution:
(d)

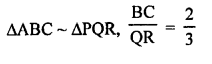
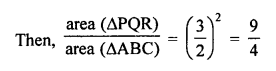
Question 42.
Solution:
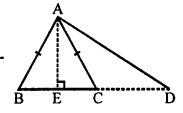
(b) In the given figure,
∆ABC is an equilateral triangle.
D is midpoint of AB and E is the midpoint of AC.

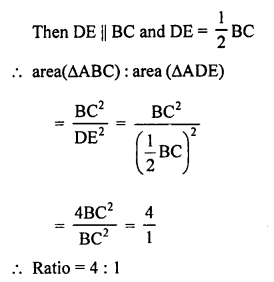
Question 43.
Solution:
(b)

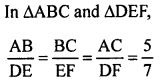
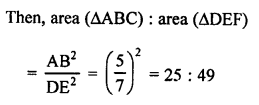
Question 44.
Solution:
(b) ∆ABC ~ ∆DEF
ar (∆ABC) = 36 cm² and ar (∆DEF) = 49 cm²
i.e. areas are in the ratio 36 : 49
Ratio in their corresponding sides = √36 : √49 = 6 : 7

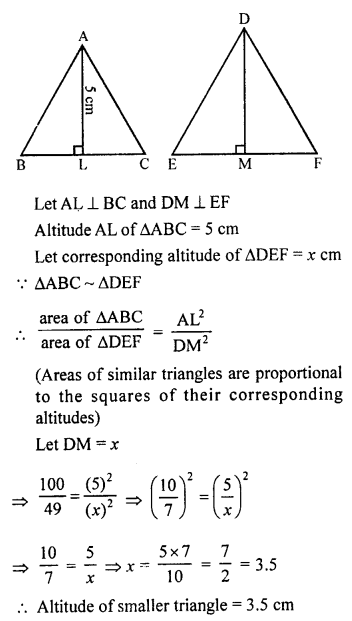
Question 45.
Solution:
(c) Two isosceles triangles have their corresponding angles equal and ratio in their areas is 25 : 36.
The ratio in their corresponding altitude
(heights) = √25 : √36 = 5 : 6 (∆s are similar)

Question 46.
Solution:
(b) The line segments joining the midpoints of a triangle form 4 triangles which are similar to the given (original) triangle.

Question 47.
Solution:
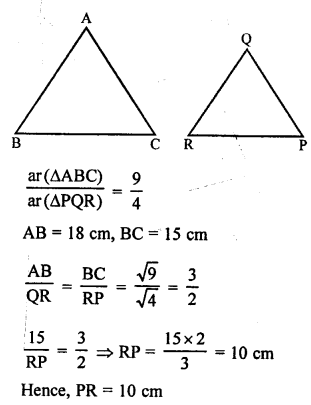
(b) ∆ABC ~ ∆QRP

Question 48.
Solution:
(c) In the given figure, O is the point of intersection of two chords AB and CD.
OB = OD and ∠AOC = 45°
∠B = ∠D (Angles opposite to equal sides)
∠A = ∠D, ∠C = ∠B (Angles in the same segment)
and ∠AOC = ∠BOD = 45° each
∆OAC ~ ∆ODB (AAA axiom)
OA = OC (Sides opposite to equal angles)
∆OAC and ∆ODB are isosceles and similar.

Question 49.
Solution:
(d) In an isosceles ∆ABC,
AC = BC
⇒ AB² = 2 AC²
⇒ AB² = AC² + AC²
⇒ AB² = AC² + BC² (AC = BC)

Converse of the Pythagoras Theorem,
∆ABC is a right triangle and angle opposite to AB = 90°
∠C = 90°

Question 50.
Solution:
(b) In ∆ABC,
AB = 16 cm, BC = 12 cm and AC = 20 cm
(Longest side)2 = 20² = 400
Sum of square on other sides = AB² + BC²
= 162 + 122 = 256 + 144 = 400
AC² = AB² + BC²
∆ABC is a right triangle.

True/False type
Question 51.
Solution:
(c) (a) False. Not always congruent.
(b) False. Two similar figures are similar if they have same shape, not size in every case.
(c) True.
(d) False. Not in each case.

Question 52.
Solution:
(a) True
(b) False, as ratio of the areas of the two similar triangles is equal to the ratio of the square of their corresponding sides.
(c) True
(d) True

Question 53.
Matching of columns : (2 marks)
Solution:

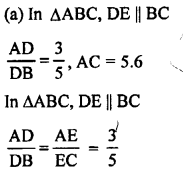
Question 54.
Solution:


correct answer is
(a) → (r)
(b) → (q)
(c) → (p)
(d) → (s)

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Very-Short-Answer and Short-Answer Questions
Question 1.
Solution:
Two properties for similarity of two triangles are:
(i) Angle-Angle-Angle (AAA) property.
(ii) Angle-Side-Angle (ASA) property.

Question 2.
Solution:
In a triangle, if a line parallel to one side is drawn, it will divide the other two sides proportionally.

Question 3.
Solution:
If a line divides any two sides of a triangle in the same ratio. Then, the line must be parallel to the third side.

Question 4.
Solution:
The line joining the midpoints of two sides of a triangle, is parallel to the third side.

Question 5.
Solution:
In two triangles, if three angles of the one triangle are equal to the three angles of the other, the triangles are similar.

Question 6.
Solution:
In two triangles, if two angles of the one triangle are equal to the corresponding angles of the other triangle, then the triangles are similar.

Question 7.
Solution:
In two triangles, if three sides of the one are proportional to the corresponding sides of the other, the triangles are similar.

Question 8.
Solution:
In two triangles, if two sides of the one are proportional to the corresponding sides of the other and their included angles are equal, the two triangles are similar.

Question 9.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of squares on the other two sides.

Question 10.
Solution:
In a triangle, if the square on the longest side is equal to the sum of the squares on the other two sides, then the angle opposite to the hypotenuse is a right angle.

Question 11.
Solution:
The ratio of their areas will be 1 : 4.

Question 12.
Solution:
In two triangles ∆ABC and ∆PQR,
AB = 3 cm, AC = 6 cm, ∠A = 70°
PR = 9 cm, ∠P = 70° and PQ= 4.5 cm

Question 13.
Solution:
∆ABC ~ ∆DEF
2AB = DE, BC = 6 cm

Question 14.
Solution:
In the given figure,
DE || BC
AD = x cm, DB = (3x + 4) cm
AE = (x + 3) cm and EC = (3x + 19) cm

Question 15.
Solution:
AB is the ladder and A is window.
AB =10 m, AC = 8 m

We have to find the distance of BC
Let BC = x m
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(10)² = 8² + x²
⇒ 100 = 64 + x²
⇒ x² = 100 – 64 = 36 = (6)²
x = 6
Distance between foot of ladder and base of the wall = 6 m.

Question 16.
Solution:
∆ABC is an equilateral triangle with side = 2a cm
AD ⊥ BC
and AD bisects BC at D

Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3 a² = √3 a cm

Question 17.
Solution:
Given : ∆ABC ~ ∆DEF
and ar (∆ABC) = 64 cm²
and ar (∆DEF) = 169 cm², BC = 4 cm.

Question 18.
Solution:
In trape∠ium ABCD,
AB || CD
AB = 2CD
Diagonals AC and BD intersect each other at O
and area(∆AOB) = 84 cm².

Question 19.
Solution:
Let ∆ABC ~ ∆DEF

Question 20.
Solution:
In an equiangular ∆ABC,
AB = BC = CA = a cm.
Draw AD ⊥ BC which bisects BC at D.

Question 21.
Solution:
ABCD is a rhombus whose sides are equal and diagonals AC and BD bisect each other at right angles.

∠AOB = 90° and AO = OC, BO = OD
AO = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 22.
Solution:
∆DEF ~ ∆GHK
∠D = ∠G = 48°
∠E = ∠H = 57°
∠F = ∠K

Now, in ∆DEF,
∠D + ∠E + ∠F = 180° (Angles of a triangle)
⇒ 48° + 57° + ∠F = 180°
⇒ 105° + ∠F= 180°
⇒ ∠F= 180°- 105° = 75°

Question 23.
Solution:
In the given figure,
In ∆ABC,
MN || BC
AM : MB = 1 : 2

Question 24.
Solution:
In ∆BMP,
PB = 5 cm, MP = 6 cm and BM = 9 cm
and in ∆CNR, NR = 9 cm

Question 25.
Solution:
In ∆ABC,
AB = AC = 25 cm
BC = 14 cm

AD ⊥ BC which bisects the base BC at D.
BD = DC = \(\frac { 14 }{ 2 }\) = 7 cm
Now, in right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
(25)² = AD² + 7²
625 = AD² + 49
⇒ AD² = 625 – 49 = 576
⇒ AD² = 576 = (24)²
AD = 24 cm
Length of altitude = 24 cm

Question 26.
Solution:
A man goes 12 m due north of point O reaching A and then 37 m due west reaching B.

Join OB,
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (12)² + (35)² = 144 + 1225 = 1369 = (37)²
OB = 37 m
The man is 37 m away from his starting point.

Question 27.
Solution:
In ∆ABC, AD is the bisector of ∠A which meets BC at D.
AB = c, BC = a, AC = b

Question 28.
Solution:
In the given figure, ∠AMN = ∠MBC = 76°
p, q and r are the lengths of AM, MB and BC Express the length of MN in terms of p, q and r.
In ∆ABC,
∠AMN = ∠MBC = 76°
But there are corresponding angles
MN || BC
∆AMN ~ ∆ABC

Question 29.
Solution:
In rhombus ABCD,
Diagonals AC and BD bisect each other at O at right angles.

AO = OC = \(\frac { 40 }{ 2 }\) = 20 cm
BO = OD = \(\frac { 42 }{ 2 }\) = 21 cm
Now, in right ∆AOB,
AB2 = AO2 + BO2 = (20)2 + (21)2 = 400 + 441 = 841
AB = √841 cm = 29 cm

Each side of rhombus = 29 cm

For each of the following statements state whether true (T) or false (F):
Question 30.
Solution:
(i) True.
(ii) False, as sides will not be proportion in each case.
(iii) False, as corresponding sides are proportional, not necessarily equal.
(iv) True.
(v) False, in ∆ABC,
AB = 6 cm, ∠A = 45° and AC = 8 cm

(vi) False, the polygon joining the midpoints of a quadrilateral is not a rhombus but it is a parallelogram.
(vii) True.
(viii) True.
(ix) True, O is any point in rectangle ABCD then
OA² + OC² = OB² + OD² is true.

(x) True.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
For the given triangle to be right-angled, the sum of the squares of the two smaller sides must be equal to the square of the largest side.
(i) 9 cm, 16 cm, 18 cm
Longest side = 18
Now (18)² = 324
and (9)² + (16)² = 81 + 256 = 337
324 ≠ 337
It is not a right triangle.
(ii) 1 cm, 24 cm, 25 cm
Here longest side = 25 cm
(25)² = 625
and (7)² x (24)² = 49 + 576 = 625
625 = 625
It is a right triangle
(iii) 1.4 cm, 4.8 cm, 5 cm
Here longest side = 5 cm
(5)² = 25
and (1.4)² + (4.8)² = 1.96 + 23.04 = 25.00 = 25
25 = 25
It is a right triangle
(iv) 1.6 cm, 3.8 cm, 4 cm
Here longest side = 4 cm
(4 )² = 16
and (1.6)² + (3.8)² = 2.56 + 14.44 = 17.00 = 17
16 ≠ 17
It is not a right triangle
(v) (a- 1) cm, 2√a cm, (a + 1) cm
Here longest side = (a + 1) cm
(a + 1)² = a² + 2a + 1
and (a – 1)² + (2 √a )² = a² – 2a + 1 + 4a = a² + 2a + 1
a² + 2a + 1 = a² + 2a + 1
It is a right triangle.

Question 2.
Solution:
A man goes 80 m from O to east side and reaches A, then he goes 150 m due north from A and reaches B.
Join OB.

In right ∆OAB,
OB² = OA²+² (Pythagoras Theorem) = (80)² + (150)² = 6400 + 22500 = 28900
⇒ OB = √28900 = 170

He is 170 m away from the starting point.

Question 3.
Solution:
A man goes 10 m due south from O and reaches A and then 24 m due west from A and reaches B.
Join OB.

Question 4.
Solution:
Length of a ladder = 13 m
Height of the window = 12 m
Distance between the foot of the ladder and building.
In the figures,

AB is ladder, A is window of building AC
AB² = AC² + BC² (Pythagoras Theorem)
⇒ (13)² = (12)² + x²
⇒ 169 = 144 + x²
⇒ x² = 169 – 144 = 25 = (5)²
x = 5
Hence, distance between foot of ladder and building = 5 m.

Question 5.
Solution:
Let length of ladder AB = x m
Height of window AC = 20 m
and distance between the foot of the ladder and the building (BC) = 15 m

AB² = AC² + BC² (Pythagoras Theorem)
⇒ x² = 20² + 15² = 400 + 225 = 625 = (25)²
x = 25
Length of ladder = 25 m

Question 6.
Solution:
Height of first pole AB = 9 m
and of second pole CD = 14 m

Let distance between their tops CA = x m
From A, draw AE || BD meeting CD at E.
Then EA = DB = 12 m CE = CD – ED = CD – AB = 14-9 = 5 m
In right ∆AEC,
AC² = AE² + CE² = 122 + 52 = 144 + 25 = 169 = (13)²
AC = 13
Distance between their tops = 13 m

Question 7.
Solution:
Height of the pole AB = 18 m
and length of wire AC = 24 m

Distance between the base of the pole and other end of the wire
BC = x m (suppose)
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
(24)² = (18)² + x²
⇒ 576 = 324 + x²
⇒ x² = 576 – 324 = 252

Question 8.

Solution:
In ∆PQR, O is a point in it such that
OP = 6 cm, OR = 8 cm and ∠POR = 90°
PQ = 24 cm, QR = 26 cm
To prove : ∆PQR is a right angled.
In ∆POR, ∠O = 90°
PR² = PO² + OR² = (6)² + (8)² = 36 + 64 = 100 = (10)²
PR = 10
Greatest side QR is 26 cm
QR² = (26)² = 676
and PQ² + PR² = (24)² + (10)² = 576 + 100 = 676
676 = 676
QR² = PQ² + PR²
∆PQR is a right angled triangle and right angle at P.

Question 9.
Solution:
In isosceles ∆ABC, AB = AC = 13 cm
AL is altitude from A to BC
and AL = 5 cm

Now, in right ∆ALB
AB² = AL² + BL²
(13)² = (5)² + BL²
⇒ 169 = 25 + BL²
⇒ BL² = 169 – 25 = 144 = (12)²
BL = 12 cm
L is mid point of BC
BC = 2 x BC = 2 x 12 = 24 cm

Question 10.
Solution:
In an isosceles ∆ABC in which
AB = AC = 2a units, BC = a units

Question 11.
Solution:
∆ABC is an equilateral triangle
and AB = BC = CA = 2a

AD ⊥ BC
D is mid point of BC
BD = DC = \(\frac { 1 }{ 2 }\) BC
= \(\frac { 1 }{ 2 }\) x 2a = a
Now, in right ∆ADB,
AB² = AD² + BD² (Pythagoras Theorem)
(2a)² = AD² + a²
⇒ 4a² – a² = AD²
⇒ AD² = 3a² = (√3 a)²
AD = √3 a = a√3 units

Question 12.
Solution:
∆ABC is an equilateral triangle in which
AB = BC = CA = 12 cm

AD ⊥ BC which bisects BC at D
BD = DC = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 12 = 6cm
Now, in right ∆ADB,
AB² = AD² + BD²
⇒ (12)² = AD² + (6)²
⇒ 144 = AD² + 36
AD² = 144 – 36 = 108
AD = √108 = √(36 x 3) = 6√3 cm

Question 13.
Solution:
Let ABCD is a rectangle in which adjacent sides.
AB = 30 cm and BC = 16 cm

AC is its diagonal.
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
= (30)² + (16)² = 900 + 256 = 1156 = (34)²
Diagonal AC = 34 cm

Question 14.
Solution:
ABCD is a rhombus
Its diagonals AC and BD bisect each other at O.

AO = OC = \(\frac { 1 }{ 2 }\) AC.
and BO = OD = \(\frac { 1 }{ 2 }\) BD
BD = 24 cm and AC = 10 cm
BO = \(\frac { 1 }{ 2 }\) x BD = \(\frac { 1 }{ 2 }\) x 24 = 12 cm
AO = \(\frac { 1 }{ 2 }\) x AC = \(\frac { 1 }{ 2 }\) x 10 = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² = (5)² + (12)² = 144 + 25 = 169 = (13)²
AB = 13
Hence, each side of rhombus = 13 cm

Question 15.
Solution:
Given : In ∆ABC, AC > AB.
D is the mid point of BC and AE ⊥ BC.
AD is joined.

To prove: AB² = AD² – BC x DE + \(\frac { 1 }{ 4 }\) BC2
Proof: In ∆AEB, ∠E = 90°
AB² = AE² + BE² …..(i) (Pythagoras Theorem)
In ∆AED, ∠E = 90°
AD² = AE² + DE²
⇒ AE² = AD² – DE² …..(ii)
Now, substitute eq. (ii) in eq. (i)
AB² = AE² + BE²
AB² = AD² – DE² + BE² [from (ii)]
AB² = (AD² – DE²) + (BD – DE)² [BE = BD – DE²]

Question 16.
Solution:

Question 17.
Solution:
Given : In ∆ABC, D is the mid point of BC, AE ⊥ BC,
BC = a, AC = b, AB = c, ED = x, AD =p and AE =
AD is joined.
To prove :

Question 18.
Solution:
Given : In ∆ABC, AB =AC
BC is produced to D and AD is joined.
To prove : (AD² – AC²) = BD x CD
Construction : Draw AE ⊥ BC.

Proof: In ∆ABC,
AB = AC and AE ⊥ BC
BE = EC
Now, in right ∆AED, ∠E = 90°
AD² = AE² + ED² …..(i)
and in right ∆AEC, ∠E = 90°
AC² = AE² + EC² …..(ii)
Now, subtracting (i) and (ii),
AD² – AC² = (AE² + ED²) – (AE² + EC²)
= AE² + ED² – AE² – EC²
= ED² – EC²
= (ED + EC) (ED – EC) (BE = EC proved above)
= BD x CD = BD x CD
AD² – AC² = BD x CD
Hence proved.

Question 19.
Solution:
Given : In ∆ABC, AB = BC and ∠ABC = 90°
∆ACD and ∆ABE are similar to each other.

To prove : Ratio between area ∆ABE and area ∆ACD.
Proof: Let AB = BC = x
Now, in right ∆ABC,
⇒ AC² = AB² + BC² = AB² + AB² = 2AB² = 2x²
∆ABE and ∆ACD are similar

Ratio between the areas of ∆ABE and ∆ACD = 1 : 2

Question 20.
Solution:
An aeroplane flies from airport to north at the speed of 1000 km/hr.
Another aeroplane flies from the airport to west at the speed of 1200 km/hr.
Period = 1\(\frac { 1 }{ 2 }\) hours
Distance covered by the first plane in 1\(\frac { 1 }{ 2 }\) hours = 1000 x \(\frac { 3 }{ 2 }\) km = 1500 km
and distance covered by another plane in 1\(\frac { 1 }{ 2 }\) hours = 1200 x \(\frac { 3 }{ 2 }\) km = 1800 km
At present, the distance between them
AB² = (BO)² + (AO)²
= (1800)² + (1500)²
= 3240000 + 2250000
= 5490000

Question 21.
Solution:
Given : In ∆ABC,
D is the mid point of BC and AL ⊥ BC
AD is joined.
To prove:

Question 22.
Solution:
AM is rod and BC is string out of rod.
In ∆BMC,
BC² = BM² + CM² = (1.8)² + (2.4)²

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
Given : Area of ∆ABC = 64 cm²
and area of ∆DEF =121 cm²
EF = 15.4 cm

Question 2.
Solution:

Question 3.
Solution:
∆ABC ~ ∆PQR
ar (∆ABC) = 4ar (∆PQR),

Question 4.
Solution:
Areas of two similar triangles are 169 cm² and 121 cm²
Longest side of largest triangle = 26 cm
Let longest side of smallest triangle = x
∆s are similar

Question 5.
Solution:
Area of ∆ABC = 100 cm²
and area of ∆DEF = 49 cm²

Question 6.
Solution:
Given : Corresponding altitudes of two similar triangles are 6 cm and 9 cm
We know that the areas of two similar triangles are in the ratio of the squares of their corresponding altitudes.
Ratio in the areas of two similar triangles = (6)² : (9)² = 36 : 81 = 4 : 9 (Dividing by 9)

Question 7.
Solution:
The areas of two similar triangles are 81 cm² and 49 cm²
Altitude of the first triangle = 6.3 cm
Let altitude of second triangle = x cm
The areas of two similar triangles are in the ratio of the squares on their corresponding altitude,
Let area of ∆ABC = 81 cm²
and area of ∆DEF = 49cm²
Altitude AL = 6 – 3 cm
Let altitude DM = x cm

Question 8.
Solution:
Areas of two similar triangles are 100 cm² and 64 cm²
Let area of ∆ABC = 100 cm²
and area of ∆DEF = 64 cm²
Median DM of ∆DEF = 5.6 cm
Let median AL of ∆ABC = x
The areas of two similar triangles is proportional to the squares of their corresponding median.

Question 9.
Solution:
Given : In ∆ABC, PQ is a line which meets AB in P and AC in Q.
AP = 1 cm, PB = 3 cm, AQ = 1.5 cm QC = 4.5 cm

Question 10.
Solution:
In ∆ABC,
DE || BC
DE = 3 cm, BC = 6 cm
area (∆ADE) = 15 cm²

Question 11.
Solution:
Given : In right ∆ABC, ∠A = 90°
AD ⊥ BC
BC = 13 cm, AC = 5 cm
To find : Ratio in area of ∆ABC and ∆ADC
In ∆ABC and ∆ADC
∠C = ∠C (common)
∠BAC = ∠ADC (each 90°)
∆ABC ~ ∆ADC (AA axiom)

Question 12.
Solution:
In the given figure ∆ABC,
DE || BC and DE : BC = 3 : 5.
In ∆ABC and ∆ADE,
DE || BC
∆ABC ~ ∆ADE

Question 13.
Solution:
In ∆ABC, D and E are the midpoints of sides AB and AC respectively.
DE || BC and DE = \(\frac { 1 }{ 2 }\) BC
∆ADE ~ ∆ABC

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
We know that two triangles are similarity of their corresponding angles are equal and corresponding sides are proportional.
(i) In ∆ABC and ∆PQR
∠A = ∠Q = 50°
∠B = ∠P = 60° and ∠C = ∠R = 70°
∆ABC ~ ∆QPR (AAA axiom)
(ii) In ∆ABC and ∆DEF
In ∆ABC,
AB = 3 cm, BC = 4.5
and in ∆DEF
DF = 6 cm, DE = 9 cm
∆ABC is not similar to ∆DEF
As in ∆ABC, ∠A is not included of two sides AB and BC.
(iii) In ∆ABC and ∆PQR
In ∆ABC,
AC = 8 cm BC = 6 cm
Included ∠C = 80°
In ∆PQR,
PQ = 4.5 cm, QR = 6 cm
and included ∠Q = 80°

(v) In ∆ABC,
∠A = 80°, ∠C = 70°
and third angle
∠B = 180° – (80° + 70°)
⇒ ∠B = 180° – 150° = 30°
In ∆MNR,
∠M = 80°, ∠N = 30°, and ∠R = [180° – (80° + 30°)]
∠R = 180° – 110° = 70°
Now, in ∆ABC
∠A = ∠M – 80°, ∠B = ∠N = 30°
and ∠C = ∠R = 70°
∆ABC ~ ∆MNR (AAA or AA axiom)

Question 2.
Solution:
In the given figure, ∆ODC ~ ∆OBA and ∠BOC =115°, ∠CDO = 70°

To find :
(i) ∠DOC
(ii) ∠DCO
(iii) ∠OAB
(iv) ∠OBA
∆ODC ~ ∆OBA
∠D = ∠B = 70°
∠C = ∠A
∠COD = ∠AOB
(i) But ∠DOC + ∠BOC = 180° (Linear pair)
⇒ ∠DOC + 115°= 180°
⇒ ∠DOC = 180° – 115° = 65°
(ii) ∠DOC + ∠CDO + ∠DCO = 180° (Angles of a triangle)
⇒ 65° + 70° + ∠DCO = 180°
⇒ 135° + ∠DCO = 180°
⇒ ∠DCO = 180° – 135°
∠DCO = 45°
(iii) ∠AOB = ∠DOC = 65° (vertically opposite angles)
∠OAB = ∠DCO = 45° (∆ODC ~ ∆OBA)
(iv) ∠OBA = ∠CDO = 70° (∆ODC ~ ∆OBA)

Question 3.
Solution:
In the given figure, ∆OAB ~ ∆OCD
AB = 8 cm, BO = 6.4 cm OC = 3.5 cm, CD = 5 cm

Question 4.
Solution:
Given : In the given figure,
∠ADE = ∠B
To prove:
(i) ∆ADE ~ ∆ABC
(ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm and BC = 4.2 cm, find DE
Proof: (i) In ∆ADE and ∆ABC
∠ADE = ∠B (given)
∠A = ∠A (common)
∆ADE ~ ∆ABC (AA axiom)

Question 5.
Solution:
∆ABC ~ ∆PQR,
PQ = 12 cm
To find AB.
Perimeter of ∆ABC = AB + BC + CA = 32 cm
Perimeter of ∆PQR = PQ + QR + RP = 24 cm
Now,
∆ABC ~ ∆PQR

Question 6.
Solution:
∆ABC ~ ∆DEF
BC = 9.1 cm, EF = 6.5 cm
Perimeter of ∆DEF = 25 cm

Question 7.
Solution:
Given : In the given figure,
∠CAB = 90° and AD ⊥ BC
To prove : ∆BDA ~ ∆BAC
If AC = 75 cm, AB = 1 m or 100 cm,
BC = 1.25 m or 125 cm
Find AD.
∆BDA ~ ∆BAC (corresponding sides and proportional)

Question 8.
Solution:
In the given figure,
∠ABC = 90°, BD ⊥ AC.
AB = 5.7 cm, BD = 3.8 cm, CD = 5.4 cm
To find BC,
In ∆ABC and ∆BDC,
∠ABC = ∠BDC (each 90°)
∠BCA = ∠BCD (common)
∆ABC ~ ∆BDC (AA axiom)
Corresponding sides are proportional

Question 9.
Solution:
In the given figure, ”
∠ABC = 90°, BD ⊥ AC
BD = 8 cm, AD = 4cm
To find CD,
Let CD = x
Now in ∆DBC and ∆BDA
∠BDC = ∠BDA (each 90°)
∠C = ∠ABD
∆DBC ~ ∆BDA
Sides are proportional

Question 10.
Solution:
In ∆ABC, P and Q are points on the sides AB and AC respectively such that
AP = 2 cm, PB = 4 cm, AQ = 3 cm and QC = 6 cm.
To prove : BC = 3 PQ

BC = 3 PQ
Hence proved.

Question 11.
Solution:
Given: ABCD is a parallelogram.
E is a point on BC and diagonal BD intersects AE at F.

To prove : AF x FB = EF x FD
Proof: In ∆AFD and ∆BFE
∠AFD = ∠BFE (vertically opposite angles)
∠ADF = ∠FBE (alternate angles)
∆AFD ~ ∆BFE (AA axiom)
\(\frac { AF }{ EF }\) = \(\frac { FD }{ FB }\)
By cross multiplication,
⇒ AF x FB = EF x FD
Hence proved.

Question 12.
Solution:
Given : In the given figure,
DB ⊥ BC, DE ⊥ AB and AC ⊥ BC

Question 13.
Solution:
In ∆ABC and ∆DEF
AC is stick and BC is its shadow.
DF is the tower and EF is its shadow
AC = 7.5 m, BC = 5 m EF = 24 m,
let DF = x m

Question 14.
Solution:
Given : In isosceles ∆ABC,
CA = CB, base AB and BA are produced in P and Q such that
AP x BQ = AC²
To prove : ∆ACP ~ ∆BCQ
Proof: In ∆ABC,
CA = CB
∠CAB = ∠CBA (Angles opposite to equal sides)
⇒ 180° – ∠CAB = 180° – ∠CBA (Subtracting each from 180°)
⇒ ∠CAP = ∠CBQ
AP x BQ = AC² (given)

Question 15.
Solution:
Given : In the given figure, ∠1 = ∠2

Question 16.
Solution:
Given : In quadrilateral ABCD,
AD = BC
P, Q, R and S are midpoints of AB, AC, CD and BD respectively.

To proof : PQRS is a rhombus.
Proof: In ∆ABC,
P and Q are the midpoints of sides AB and AC respectively.
PQ || BC ……(i)

Question 17.
Solution:
In the given circle, two chords AB and CD intersect each other at P inside the circle.
To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof:
(a) In ∆PAC and ∆PDB
∠APC = ∠BPD (Vertically opposite angles)
∠A = ∠D (Angles in the same segment)
∆PAC ~ ∆PDB (AA axiom)
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA x PB = PC x PD
Hence proved.

Question 18.
Solution:
In a circle, two chords AB and CD intersect each other at the point P outside the circle.
AC and BD are joined.

To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof: In the circle, quadrilateral ABDC is a cyclic.
Ext. ∠PAC = ∠D
Now, in ∆PDB and ∆PAC
∠P = ∠P (common)
∠PAC = ∠D (proved)
∆PDB ~ ∆PAC (AA axiom)
or ∆PAC ~ ∆PBD
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA . PB = PC . PD
Hence proved

Question 19.
Solution:
Given : In right ∆ABC, ∠B = 90°
D is a point on hypotenuse AC such that
BD ⊥ AC and DP ⊥ AB and DQ ⊥ BC.

To prove :
(a) DQ² = DP . QC
(b) DP² = DQ . AP
Proof: AB ⊥ BC and DQ ⊥ BC
AB || DQ
DP ⊥ AB
DP || BC
Now, AB or PB || DQ and BC or BQ || DP BQDP is a rectangle
BQ = DP and BP = DQ
Now, in right ∆BQD
∠1 + ∠2 = 90° …..(i)
Similarly in rt. ∆DQC,
∠3 + ∠4 = 90° (DQ ⊥ BC) …(ii)
and in right ∆BDC,
∠2 + ∠3 = 90° …(iii)
∠BDC = 90° (BD ⊥ AC)
From (i) and (ii),
∠1 = ∠3
and from (ii) and (iii),
∠2 = ∠4
Now, in ∆BQD and ∆DQC
∠1 = ∠3
∠2 = ∠4 (proved)
∆BQD ~ ∆DQC (AA axiom)
\(\frac { BQ }{ DQ }\) = \(\frac { DQ }{ QC }\)
⇒ DQ² = BQ x QC
⇒ DQ² = DP x QC
(b) Similarly, we can prove that
∆PDA ~ ∆PBD
\(\frac { PD }{ PB }\) = \(\frac { AP }{ DP }\)
⇒ DP² = BP x AP
⇒ DP² = DQ . AP (BP = DQ)
Hence proved.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.