Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18C
Question 1.
The radius of a circle is 8cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10cm from its centre.
Solution:
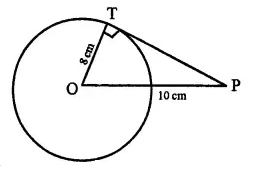
OP = 10 cm,
raduis OT = 8 cm
∵ OT ⊥ PT
∴ In right ΔOTP,
OP2 = OT2+PT2
⇒ (10)2 =(8)2+PT2
⇒ 100 = 64+PT2
⇒ PT2 = 100-64 = 36
∴ PT = \( \sqrt{36} \) = 6 cm
Question 2.
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
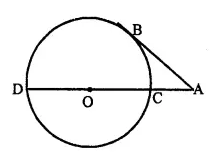
Solution:
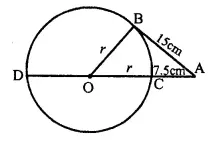
∠OBA = 90° (Radius through the point of contact is perpendicular to the tangent)
⇒ OB2 = OA2 – AB2 ⇒ r2 = (r + 7.5)2 – 152
⇒ r2 = r2 + 56.25 + 15r – 225 168.75
⇒ 15r= 168.75
⇒ r =\(\frac { 168.75 }{ 75 }\) ⇒ r=11.25
Hence, radius of the circle = 11.25 cm
Question 3.
Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
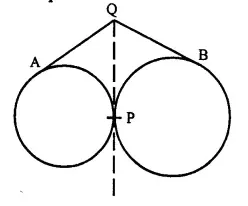
Solution:
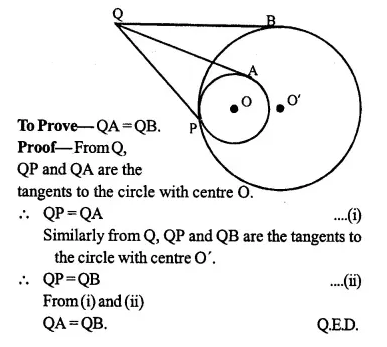
Given: Two circles with centre O and O’ touches at P externally. Q is a point on the common tangent through P.
QA and QB are tangents from Q to the circles respectively.
To Prove: QA=QB.
Proof: From Q, QA and QP are the tangents to the circle with centre O
∴ QA=QP ….(i)
Similarly, QP and QB are the tangents to the circle with centre O’
∴ QP=QB ….(ii)
From (i) and (ii)
QA=QB Q.ED.
Question 4.
Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
Solution:
Given: Two circles with centre O and O’ touch each other internally at P. Q is a point on the common tangent through P. QP an QB are tangents from Q to the circles respectively.
Question 5.
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
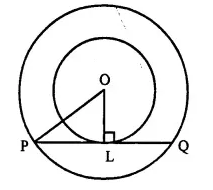
Solution:
Given: Two concentric circles with radius 5 cm and 3 cm with centre O. PQ is the chord of the outer circle which touches the inner circle at L. Join OL and OP.
OL=3 cm, OP = 5 cm

Question 6.
Three circles touch each other externally. A triangle is formed when the centres of these circles are j oined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
Solution:
Three circles touches each other externally
Δ ABC is formed by joining the centres A, B and C of the circles.
AB = 6 cm, AC = 8 cm and BC = 9 cm
Let radii of the circles having centres A, B and C be r1, r2, r3 respectively
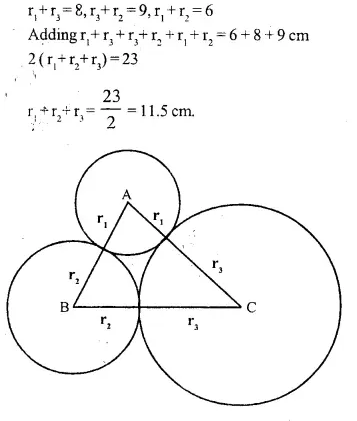
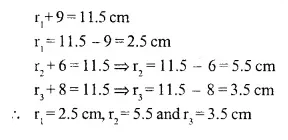
Question 7.
If the sides of a quadrilateral ABCD touch a circle, prove that: AB + CD = BC + AD.
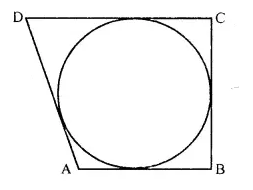
Solution:
Given: A circle touches the sides AB, BC, CD and DA of quad. ABCD at P,Q,R and S respectively.
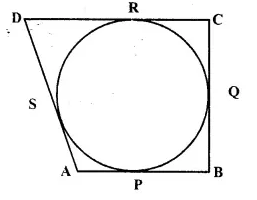
To Prove: AB + CD = BC + AD
Proof: Since AP and AS are the tangents to the circle from external point A.
∴ AP = AS ….(i)
Similarly, we can prove that,
BP=BQ ….(ii)
CR=CQ …(iii)
DR=DS ….(iv)
Adding, we get:
AP + BP + CR + DR = AS + BQ + CQ + DS
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC
Hence AB + CD = BC + AD. Q.E.D.
Question 8.
If the sides of a parallelogram touch a circle (refer figure of Q/7) prove that the parallelogram is a rhombus.
Solution:
Given : The sides AB, BC, CD and DA of ||gm ABCD touches the circle at P, Q, R and S respectively.
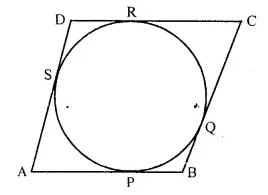
To Prove : ABCD is a rhombus.
Proof : From A, AP and AS are the tangents to the circle.
∴ AP = AS ….(i)

Question 9.
From the given figure, prove that:
AP + BQ + CR = BP + CQ + AR.
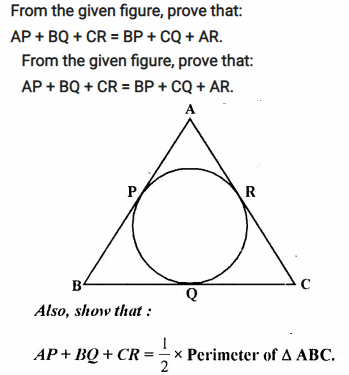
Solution:
Given: In the figure, sides of Δ ABC touch a circle at P, Q, R.
To Prove:
(i) AP + BQ + CR = BP + CQ + AR
(ii) AP + BQ + CR = \(\frac { 1 }{ 2 }\) Perimeter of Δ ABC.
Proof :
∵ From B, BQ and BP are the tangents to the circle.
∴ BQ = BP ….(i)
Similarly we can prove that
AP= AR ……… (ii)
and CR = CQ …..(iii)
Adding we get
AP + BQ + CR = BP + CQ + AR ….(iv)
Adding AP + BQ + CR both sides,
2(AP + BQ + CR) = AP + PQ + CQ + QB + AR+CR.
⇒ 2 (AP + BQ + CR) = AB + BC + CA
∴ AP + BQ + CR = \(\frac { 1 }{ 2 }\) (AB + BC + CA)
= \(\frac { 1 }{ 2 }\) Perimeter of Δ ABC. Q.E.D.
Question 10.
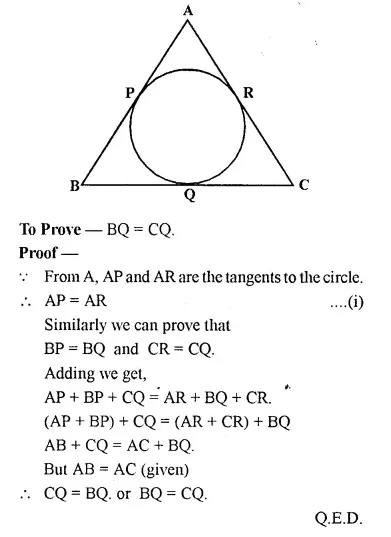
In the figure of Q.9 if AB = AC then prove that BQ = CQ.
Solution:
Given: A circle touches the sides AB, BC, CA of Δ ABC at P, Q and R respectively, and AB = AC
Question 11.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centres if
(i) they touch each other externally,
(ii) they touch each other internally.
Solution:
Radius of bigger circle = 6.3 cm
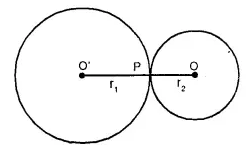
and raduis of smaller circle = 3.6 cm.
(i) Two circles touch each other at P externally. 0 and O’ are the centres of the circles.
Join OP and OP’
OP = 3.6 cm, O’P = 6.3 cm.
Adding we get
OO’ = OP + O’P = 3.6 + 6.3 = 9.9 cm
(ii) If the circles touch each other internally at P.
OP = 3.6 cm and O’P = 6.3 cm.
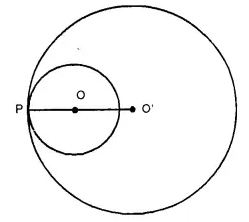
∴ OO’ = O’P – OP
= 6.3 – 3.6 = 2.7 cm
Question 12.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP,
(ii) OP is the ⊥ bisector of chord AB.
Solution:
Given: A circle with centre 0. A point P out side the circle. From P, PA and PB are the tangents to the circle, OP and AB are joined.
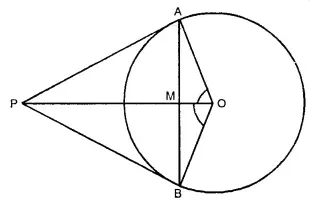
To prove:
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of chord AB.
Proof : In ∆ AOP and ∆ BOP,
AP = BP (Tangents from P to the circle.)
OP = OP (Common)
OA = OB (Radii of the same circle)
∴ ∆ AOP s ∆ BOP (SSS postulate)
∴∠AOP = ∠BOP (C.P.C.T.)
Now in ∆ OAM and ∆ OBM,
OA = OB (Radii of the same circle)
OM = OM (Common)
∠AOM = ∠BOM (Proved ∠AOP = ∠BOP)
∴ ∆ OAM = ∆ OBM (S.A.S. Postulate)
∴ AM = MB (C.P.C.T.)
and ∠OMA = ∠OMB (C.P.C.T.)
But ∠OMA + ∠OMB = 180° (Linear pair)
∴ ∠OMA = ∠OMB = 90°
Hence OM or OP is the perpendicular bisector of AB. Q.E.D.
Question 13.
In the given figure, two circles touch each other externally at point P, AB is the direct common tangent of these circles. Prove that:
(i) tangent at point P bisects AB.
(ii) Angle APB = 90°
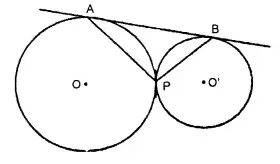
Solution:
Given : Two circles with centre O and O’ touch each other at P externally. AB is the direct common tangent touching the circles at A and B respectively.
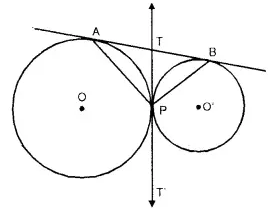
AP, BP are joined. TPT’ is the common tangent to the circles.
To Prove : (i) TPT’ bisects AB (ii) ∠APB = 90°
Proof :
∵ TA and TP arc the tangents to the circle
∴ TA = TP …(i)
Similarly TP. = TB ….(ii)
From (i) and (ii)
TA = TB
∴ TPT’ is the bisector of AB.
Now in ∆ ATP
TA = TP
∴ ∠TAP = ∠TPA
Similarly in A BTP.
∠TBP = ∠TPB
Adding we get.
∠TAP + ∠TBP = ∠APB
But ∠TAP + ∠TBP + ∠APB = 180°
∴ ∠APB = ∠TAP + ∠TBP = 90°. Q.E.D.
Question 14.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that:
∠PAQ = 2∠OPQ
Solution:
Given: A circle with centre O. two tangents PA and QA are drawn from a point A out side the circle OP, OQ. OA and PQ are joined.
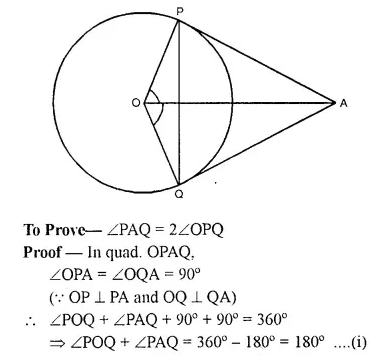
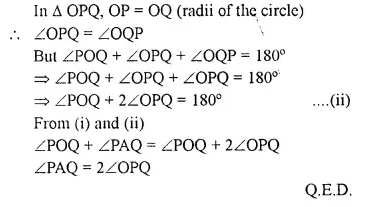
Question 15.
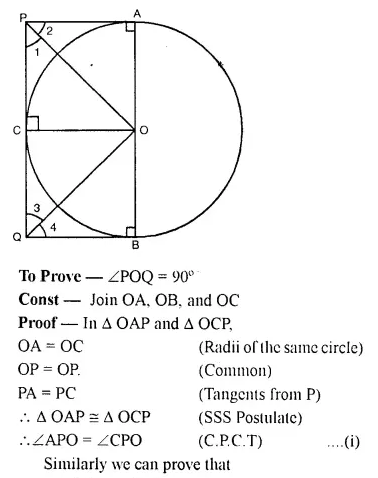
Two parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
Solution:
Given: A circle with centre O, AP and BQ are two parallel tangents. A third tangent PQ intersect them at P and Q. PO and QO are joined

Question 16.
ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
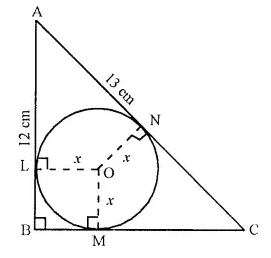
Calculate the value of x, the radius of the inscribed circle.
Solution:
In ∆ ABC, ∠B = 90°
OL ⊥ AB, OM ⊥ BC and
ON ⊥ AC.
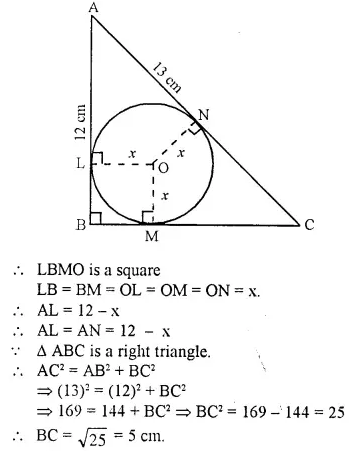
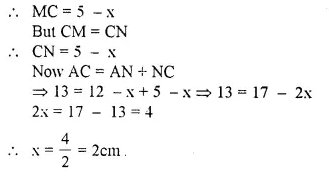
Question 17.
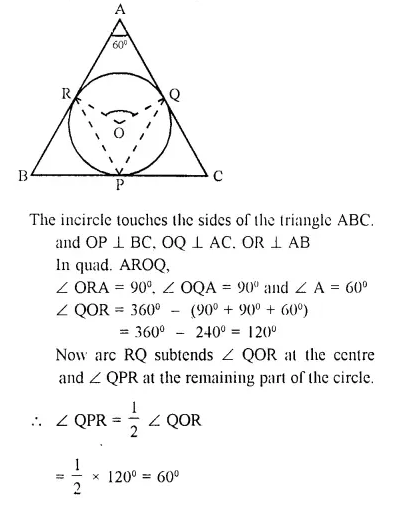
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
(i) ∠ QOR
(ii) ∠ QPR given that ∠ A = 60°.
Solution:
Question 18.
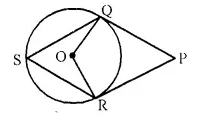
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60°, calculate:
(i) ∠ QOR
(ii) ∠ OQR
(iii) ∠ QSR.
Solution:
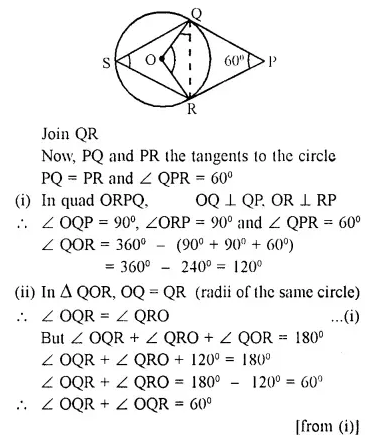
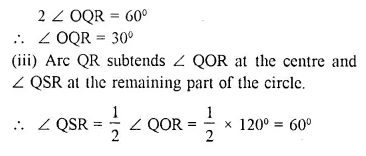
Question 19.
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
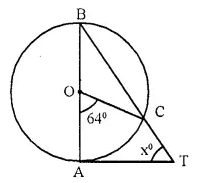
Solution:
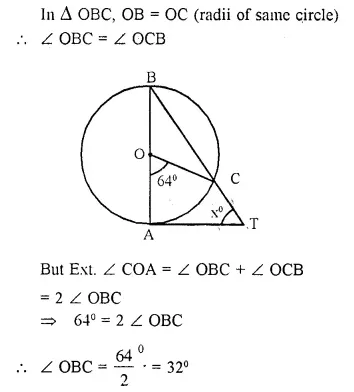
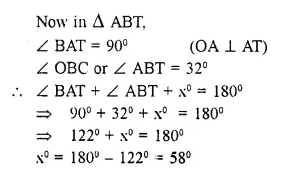
Question 20.
In quadrilateral ABCD; angle D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm. Find the radius of the circle. |1990]
Solution:
BQ and BR arc the tangenls from B to the circle.
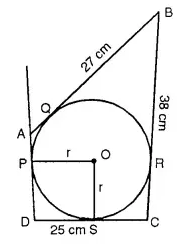
∴ BR = BQ = 27 cm.
∴ RC = 38-27 = 11 cm.
Since CR and CS are the tangents from C to the circle
∴ CS = CR= 11 cm.
∴ DS = 25 – 11 = 14 cm.
DS and DP are the tangents to the circle
∴ DS = DP
∴ ∠ PDS = 90° (given)
and OP ⊥ AD, OS ⊥ DC
∴ Radius = DS = 14 cm
Question 21.
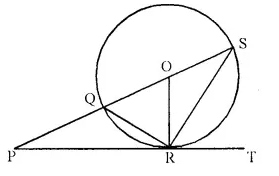
In the given, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given ∠ SPR = x° and ∠ QRP = y°;
Prove that
(i) ∠ ORS = y°
(ii) Write an expression connecting x and y. [1992]
Solution:
∠ QRP = ∠ OSR = y (Angles in the alternate segment)
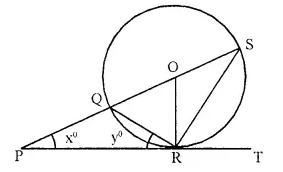
But OS = OR (radii of the same circle)
∴ ∠ ORS = ∠ OSR = y°
∴ OQ = OR (radii of the same circle)
∴ ∠ OQR = ∠ ORQ = 90° – y° ….(i) (OR ⊥ PT)
But in ∆ PQR,
Ext. ∠ OQR = x° + y° ….(ii)
from (i) and (ii)
x° + y° = 90° – y°
⇒ x° + 2y° = 90°
Question 22.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50°; calculate :
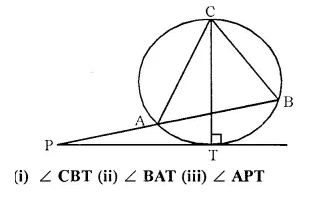
Solution:
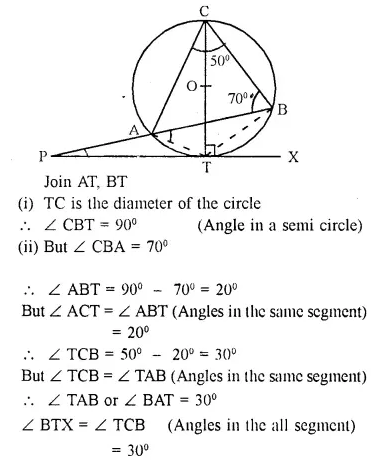
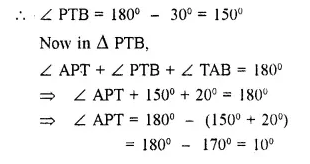
Question 23.
In the given figure. O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC 80°; find the angle BAC. [1996]
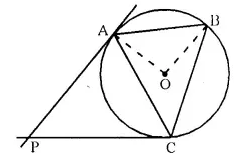
Solution:
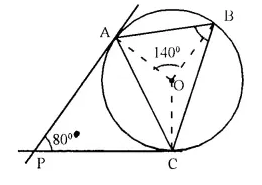
Join OC
∴ PA and PC are the tangents
∴ OA ⊥ PA and OC ⊥ PC
In quad APCO,
∴ ∠ APC + ∠ AOC = 180°
⇒ 80° + ∠ AOC = 180°
∴ ∠ AOC = 180° – 80° = 100°
∠ BOC = 360° – (∠ AOB + ∠ AOC)
= 360° – (140° + 100°)
= 360° – 240° = 120°
Now arc BC subtends ∠ BOC at the centre and ∠BAC at the remaining part of the circle.
∴ ∠ BAC = \(\frac { 1 }{ 2 }\)∠BOC
= \(\frac { 1 }{ 2 }\) x 120° = 60°
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.