Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E
Question 1.
Find the slope and y-intercept of the line :
(i) y = 4
(ii) ax – by = 0
(iii) 3x – 4y = 5
Solution:
(i) y = 4 ⇒ y = 0x + 4
Here slope = 0 and y-intercept = 4
(ii) ax – by = 0
⇒ by = ax
⇒ y = \(\frac { a }{ b }\) x + 0
Here, slope = \(\frac { a }{ b }\) and y-intercept = 0
(iii) 3x – 4y = 5
⇒ – 4y = 5 – 3x
⇒ 4y = 3x – 5
⇒ y = \(\frac { 3 }{ 4 }\) x + \(\frac { -5 }{ 4 }\)
Here, slope = \(\frac { 3 }{ 4 }\) and y- intercept = \(\frac { -5 }{ 4 }\)
Question 2.
The equation of a line is x – y = 4. Find its – slope and y-intercept. Also, find its inclination.
Solution:
x – y = 4
writing the equation in form of y = mx + c
x = 4 + y
⇒ y = x – 4
Slope = 1 and y-intercept = – 4
Slope = 1
⇒ tanθ = 1
⇒ θ = 45°
Question 3.
(i) Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0 ?
(ii) Is the line x – 3y = 4 perpendicular to the line 3x – y = 7 ?
(iii) Is the line 3x + 2y = 5 parallel to the line x + 2y = 1 ?
(iv) Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
Solution:
(i) 3x + 4y + 7 = 0
Writing the equation in form of y = mx + c
4y = -3x – 7
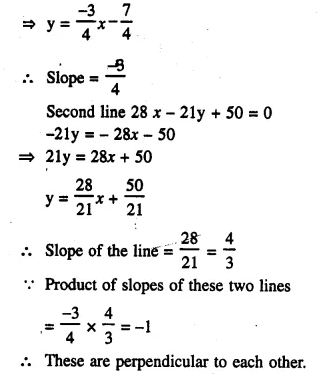
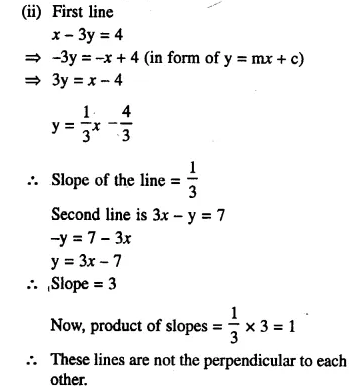
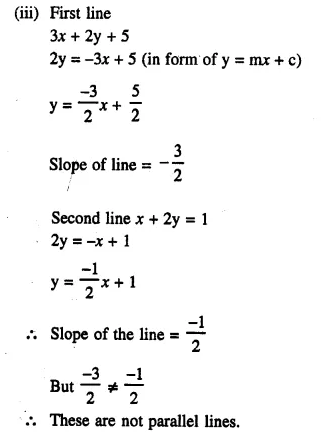
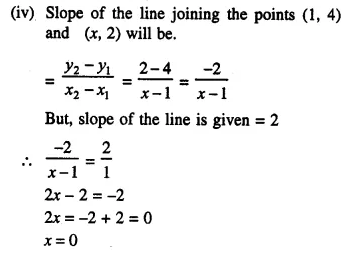
Question 4.
Find the slope of the line which is parallel to:
(i) x + 2y + 3 = 0
(ii) \(\frac { x }{ 2 }\) – \(\frac { y }{ 3 }\) – 1 = 0
Solution:
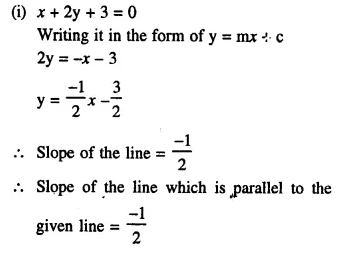

Question 5.
Find the slope of the line which is perpendicular to:
(i) x – \(\frac { y }{ 2 }\) + 3 = 0
(ii) \(\frac { x }{ 3 }\) – 2y = 4
Solution:
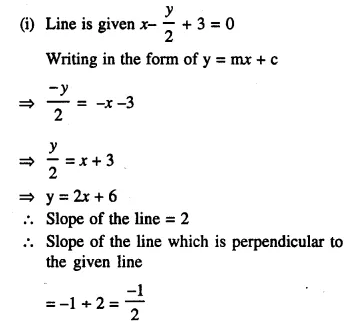
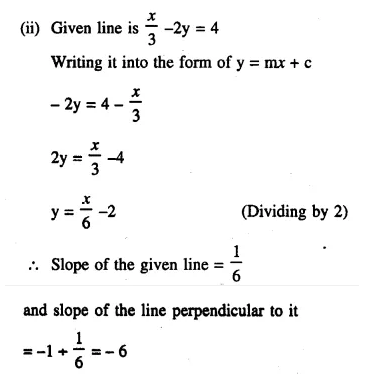
Question 6.
(i) Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.
(ii) Lines mx + 3y + 7 = 0 and 5x- ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
Solution:
(i) Writing the given equations in the form of y = mx + c, we get:
-by = -2x -5
by = 2x + 5
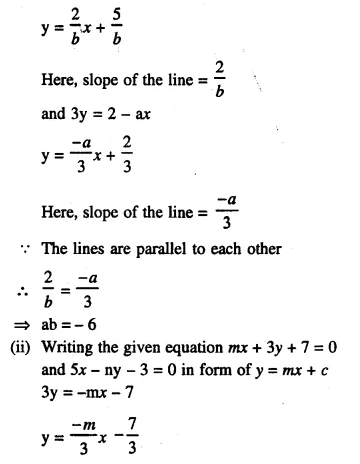
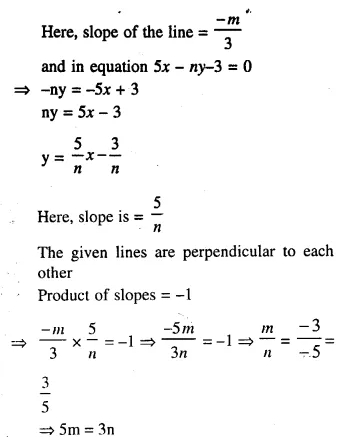
Question 7.
Find the value of p if the lines, whose equations are 2x – y + 5 = 0 and px + 3y = 4 are perpendicular to each other.
Solution:
Writing the given equations 2x – y + 5 = 0 and px + 3y = 4 in form of y = mx + c
2x – y + 5 = 0
-y = -2x -5
y = 2x + 5
Here, slope of the line = 2
Again, px + 3y = 4
3y = – px + 4
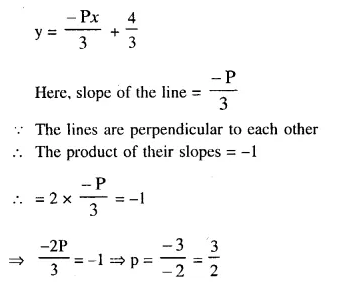
Question 8.
The equation of a line AB is 2x – 2y + 3 = 0.
(i) Find the slope of the line AB.
(ii) Calculate the angle that the line AB makes with the positive direction of the x-axis.
Solution:
The line AB is given.2* – 2y + 3 = 0
Writing it in the form of y = mx + c
-2y = -2x – 3
⇒ 2y = 2x + 3
⇒ y = x + \(\frac { 3 }{ 2 }\)
Here, slope of the line = 1
Angle of inclination = tanθ
tanθ = 1
θ = 45°
Question 9.
The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.
Solution:
Writing the given lines 4x + 3y = 9 and px – 6y + 3 = 0 in the form of y = mx + c
4x + 3y = 9
⇒ 3y = – 4x + 9
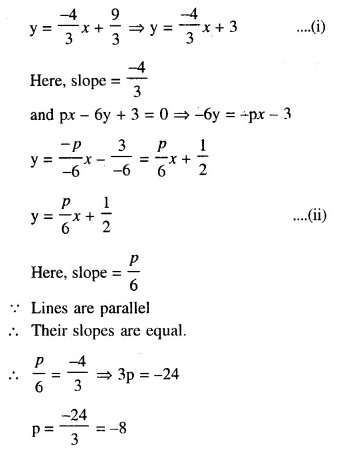
Question 10.
If the lines y = 3x + 7 and 2y +px = 3 are perpendicular to each other, find the value of p. (2006)
Solution:
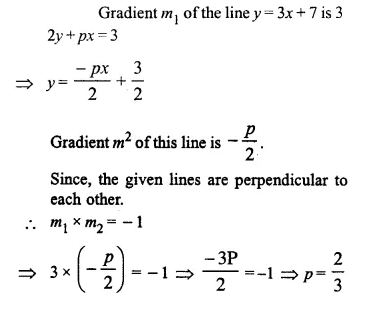
Question 11.
The line through A (-2, 3) and B (4, 6) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
Gradient (mx) of the line passing through the points A (-2, 3) and B (4, b)
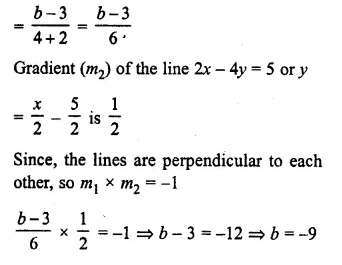
Question 12.
Find the equation of the line passing through (-5, 7) and parallel to
(i) x-axis
(ii) y-axis.
Solution:
(i) Slope of the line parallel to x-axis = 0
Equation of line passing through (-5, 7) whose slope is 0.
y – 7 = 0 [x – (-5)]
⇒ y – 7 = 0
⇒ y = 7
(ii) Slope of the line parallel to y-axis = 0
y – y1 = m (x – x1)
⇒ 0 = x – x1
⇒ x + 5 = 0
Question 13.
(i) Find the equation of the line passing through (5, -3) and parallel to x – 3y = 4.
(ii) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1). (2007)
Solution:
(i) Writing the equation x – 3y = 4 in form of y = mx + c
-3y = -x + 4
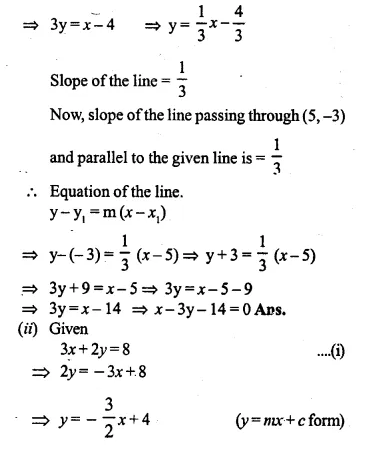
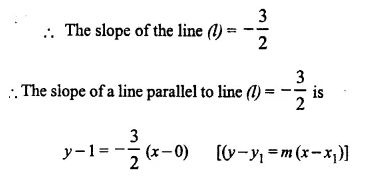
⇒ 2y – 2 = -3x
⇒ 3x + 2y – 2 = 0
Which is the required equation.
Question 14.
Find the equation of the line passing through (-2, 1) and perpendicular to 4x + 5y = 6.
Solution:
Writing the equation 4x + 5y = 6 in form of y = mx + c
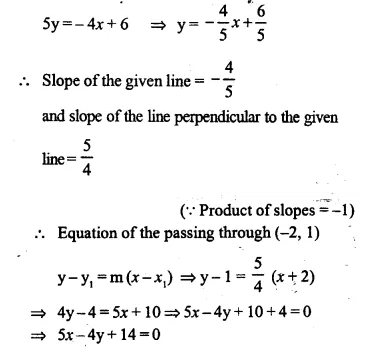
Question 15.
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, -3) and (0, 3).
Solution:
The perpendicular of the line segment bisects it.
Co-ordinates of mid-point of the line segment which is obtained by joining the points (6, -3) and (0, 3)
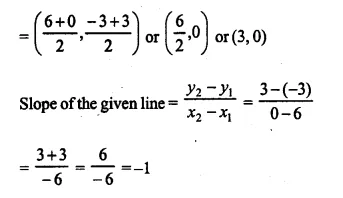
Slope of the line perpendicular to it = 1 (Product of slopes = -1)
Equation of the perpendicular bisector is y – y1 = m (x – x1)
y – 0 = 1 (x – 3)
y = x – 3
Question 16.
In the following diagram, write down:
(i) the co-ordinates of the points A, Band C.
(ii) the equation of the line through A and parallel to BC.
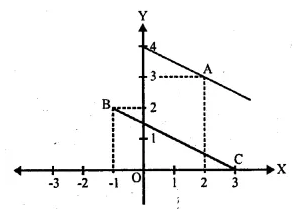
Solution:
(i) From the figure, the see that co-ordinates of A are (2, 3), B are (-1, 2) and C are (3, 0)
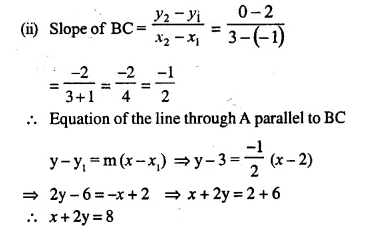
Question 17.
B (-5, 6) and D (1, 4) are the vertices of rhombus ABCD. Find the equation of diagonal BD and of diagonal AC.
Solution:
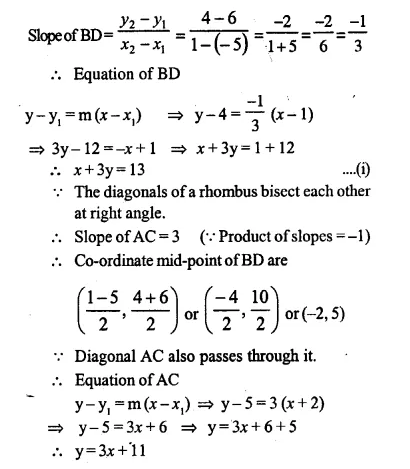
Question 18.
A = (7, -2) and C = (-1, – 6) are the vertices of a square ABCD. Find the equation of the diagonals AC and BD.
Solution:

Question 19.
A (1, -5), B (2, 2) and C (-2, 4) are the vertices of the ∆ABC, find the equation of:
(i) the median of the triangle through A.
(ii) the altitude of the triangle through B.
(iii) the line through C and parallel to AB.
Solution:
(i) Let D be the mid-point of BC
co-ordinates mid-point of
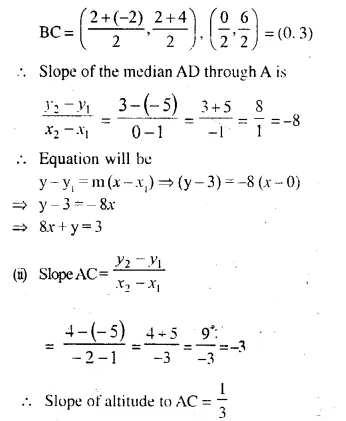
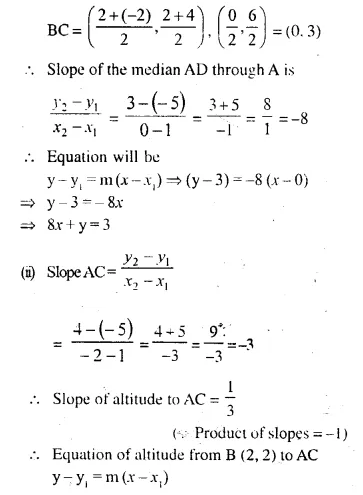
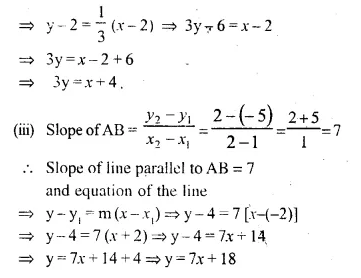
Question 20.
(i) Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
(ii) AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin. [1995]
Solution:
(i) Write the equation 2y = 3x + 5 in the form of y = mx + c. We get:
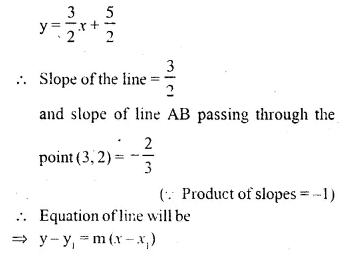
y – 2 = \(\frac { -2 }{ 3 }\) (x – 3)
⇒ 3y – 6 = -2x + 6
⇒ 2x + 3y = 6 + 6
⇒ 2x + 3y = 12 …… (i)
(ii) AB meets the x-axis at A
ordinate (y) of A = 0 i.e. y = 0
Substituting, the value of y in (i)
2x + 3 x 0 = 12
⇒ 2x = 12
⇒ x = 6
Co-ordinates of A are (6, 0)
Again. AB meets y-axis at B
Abscissa of B = 0 i.e. x = 0
Substituting the value of x in (i)
2 x 0 + 3y = 12
⇒ y = 4
Co-ordinates of B are (0, 4)
Area of ∆OAB = \(\frac { 1 }{ 2 }\) x Base x altitude
= \(\frac { 1 }{ 2 }\) x 4 x 6 = 12 square units
Question 21.
The line 4x – 3y + 12 = 0 meets the x-axis at A. Write the co-ordinates of A.
Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
Solution:
The line 4x – 3y + 12 = 0 meets x-axis at A.
Ordinates of A = 0. i.e. y = 0
Substituting, the value of y in the equation
4x – 3 x 0 + 12 = 0
⇒ 4x + 12 = 0
⇒ 4x = -12
⇒ x = -3
Co-ordinates of A are (-3, 0)
Writing the equation 4x – 3y + 12 = 0 in form of y = mx + c
⇒ -3y = -4x – 12
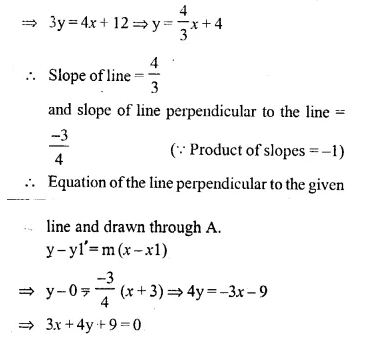
Question 22.
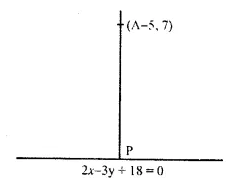
The point P is the foot of perpendicular from A (-5, 7) to the line is 2x – 3y + 18 = 0. Determine:
(i) the equation of the line AP.
(ii) the co-ordinates of P.
Solution:
Write the equation in form of y = mx + c
2x – 3y + 18 = 0
⇒ -3y = -2x – 18
⇒ y = \(\frac { 2 }{ 3 }\) x + 6 (Dividing by 3)
Slope of the line = \(\frac { 2 }{ 3 }\)
and slope of the line perpendicular to it = \(\frac { -3 }{ 2 }\) (Product of slopes = -1)
(i) Equation of line AP perpendicular to the given line and drawn through A (-5, 7)
y – y1 = m (x – x1)
⇒ y – 7 = \(\frac { -3 }{ 2 }\) (x + 5)
⇒ 2y – 14 = -3x – 15
⇒ 3x + 2y – 14 + 15 = 0
⇒ 3x + 2y + 1 = 0
(ii) P is the point of intersection of these lines
we will solve their equations
2x – 3y + 18 = 0 ….(i)
3x + 2y + 1 = 0 ….(ii)
Multiplying (i) by 2 and (ii) by 3, we get
4x – 6y + 36 = 0
9x + 6y + 3 = 0
Adding, we get:
13x + 39 = 0
⇒ 13x = -39
⇒ x = -3
Now, substituting the value of x in (i)
2(-3) – 3y + 18 = 0
⇒ -6 – 3y + 18 = 0
⇒ -3y + 18 – 6 = 0
⇒ -3y + 12 = 0
⇒ -3y = -12
⇒ 3y = 12
⇒ y = 4
Co-ordinates of P are (-3, 4)
Question 23.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Solution:
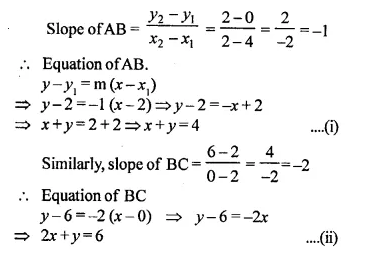
AB meets y- axis at P
abscissa of P = 0 i. e. x = 0
Substituting the value of y in (i)
0 + y = 4
⇒ y = 4
Co-ordinates of P are (0, 4)
BC meets x-axis at Q
ordinate of Q = 0 i.e. y = 0
Substituting, the value of y in (ii),
2x + 0 = 6
⇒ 2x = 6
⇒ x = 3
Co-ordinates of Q are (3, 0)
Question 24.
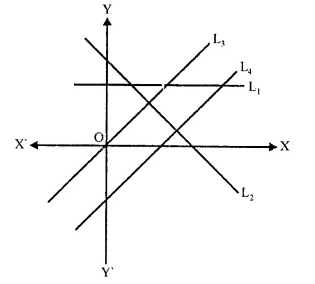
Match the equations A, B, C, and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A = y = 2x;
B = y – 2x + 2 = 0;
C = 3x + 2y = 6;
D = y = 2 [1996]
Solution:
A → L3,
B → L4,
C → L2,
D → L1
Question 25.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line. (2014)
Solution:
A (a, 3), B (2,1) and C (5, a) are collinear.
Slope of AB = Slope of BC
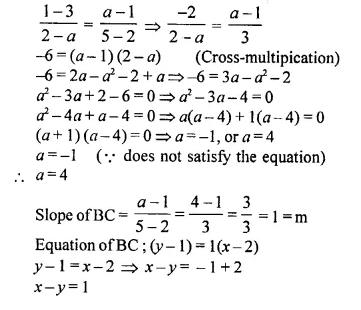
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.