Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E
Question 1.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(i) (1, 3)
(ii) (0, 5)
(iii) (-5, 0)
(iv) (5, 5)
(v) (2, -1.5)
(vi) (-2, -1.5)
Solution:
Equation of given line x – 2y + 5 = 0
(i) Substituting x = 1, y = 3, in the given equation.
1 – 2 x 3 + 5 = 0 ⇒ 1 – 6 + 5 = 0 ⇒ 0 = 0, which is true.
(1, 3) satisfies the equation.
(ii) Substituting x = 0 , y = 5 in the given equation
0 – 2 x 5 + 5 = 0 ⇒ 0 – 10 + 5 = 0 ⇒ -5 = 0, which is not true.
( 0, 5) does not satisfy the equation.
(iii) Substituting x = – 5, y = 0 in the given equation
-5 – 2 x 0 + 5 = 0 ⇒ -5 – 0 + 5 = 0 ⇒ 0 = 0 which is true.
(-5, 0) satisfies the equation.
(iv) Substituting x = 5, y = 5 in the given equation.
– 5 – 2 x 5 + 5 = 0 ⇒ -5 – 10 + 5 = 0 ⇒ 0 = 0 which is true.
(5, 5) satisfies the equation.
(v) Substituting x = 2, y = -1.5 in the given equation.
2 – 2 x (- 1.5) + 5 = 0 ⇒ 2 + 3 + 5 = 0 ⇒ 10 = 0. which is not true.
(2, -1.5) does not satisfy the equation.
(vi) Substituting x = -2, y = -1.5 in the given equation
– 2 – 2 x (-1.5) + 5 = 0 ⇒ – 2 + 3 + 5 = 0 ⇒ 6 = 0, which is not true.
(-2, -1.5) does not satisfies the equation.
Question 2.
State, true or false :
(i) the line \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0 passes through the point (2, 3).
(ii) the line \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0 passes through the point (4, -6).
(iii) the point (8, 7) lies on the line y – 7 = 0
(iv) the point (-3, 0) lies on the line x + 3 = 0
(v) if the point (2, a) lies on the line 2x – y = 3, then a = 5.
Solution:
(i) Equation of the line is \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0
and co-ordinates of point are (2, 3)
If the point is on the line, then it will satisfy the equation.
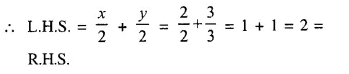
(2, 3) is not on the line
(ii) Equation of the line is \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0
and co-ordinates of point are (4, -6)
If the point is on the line, then it will satisfy the equation
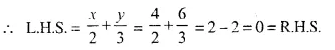
Hence, point (4, -6) is on the line.
(iii) Equation of line is y – 7 = 0 and the co-ordinates of point are (8, 7)
If the point is on the line, then it will satisfy the equation
L.H.S. = y – 7 = 7 – 7 = 0 = R.H.S.
Hence, point (8, 7) is on the line.
(iv) Equation of the line is x + 3 = 0 and co-ordinates of point are (-3, 0)
If the point is on the line, then it will satisfy the equation.
L.H.S. = x + 3 = -3 + 3 = 0 = R.H.S.
Hence, the point (-3, 0) is on the line.
(v) Equation of the line is 2x – y = 3
and co-ordinates of the point are (2, a)
If the point is on the line, then it will satisfy the equation.
L.H.S. = 2x – y = 2 x 2 – a = 4 – a
R.H.S. = 3
4 – a = 3 ⇒ 4 + 3 = a ⇒ a = 7
But a = 5 given, therefore it is not on the line.
(i) False (ii) True (iii) True (iv) True (v) False.
Question 3.
The line given by the equation 2x – \(\frac { y }{ 3 }\) = 7 passes through the point (k, 6); calculate the value of k.
Solution:
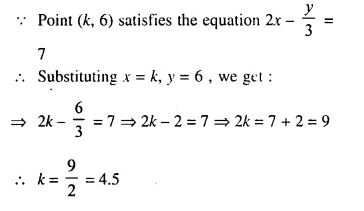
Question 4.
For what value of k will the point (3, -k) lie on the line 9x + 4y = 3 ?
Solution:
Point (3, -k) satisfies the equation 9x + 4y = 3
Substituting x = 3 , y = -k, we get :
9 x 3 + 4 (- k), = 3
⇒ 27 – 4k = 3
⇒ – 4k = 3 – 27
⇒ – 4k = – 24
⇒ k = 6
Question 5.
The line \(\frac { 3x }{ 5 }\) – \(\frac { 2y }{ 3 }\) + 1 = 0, contains the point (m, 2m – 1); calculate the value of m.
Solution:
Point (m, 2m -1) satisfies the equation
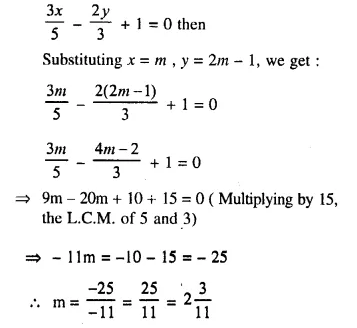
Question 6.
Does the line 3x – 5y = 6 bisect the join of (5, -2) and (-1, 2) ?
Solution:
Line 3x – 5y = 6 bisect the join of points (5, -2) and (-1, 2)
The mid-point of (5, -2) and (-1, 2) satisfies the equation.
Now, mid-point of (5, -2) and (-1, 2)
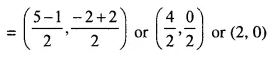
Now, substituting x = 2, y = 0, in the given equation
3 x 2 – 5 x 0 = 6 ⇒ 6 – 0 = 6 ⇒ 6 = 6 which is true. .
Given line bisect the join of points (5, -2) and (-1, 2)
Question 7.
(i) The line y = 3x – 2 bisects the join of (a, 3) and (2, -5), find the value of k.
(ii) The line x – 6y + 11 = 0 bisects the join of (8, -1) and ( 0, k). Find the value of k.
Solution:
(i) line y = 3x – 2 bisects the join of (a, 3) and (2, -5)
Mid-point join of there points satisfies it.
Now, mid-point of (a, 3) and (2, -5) is
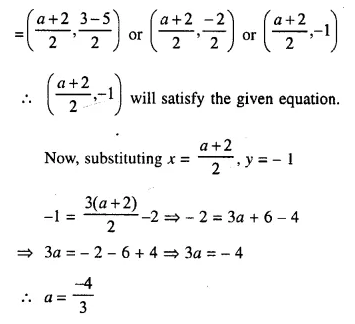

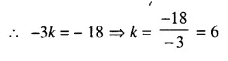
Question 8.
(i) The point (-3, -2) lies on the line ax + 3y + 6 = 0, calculate the value of ‘a’
(ii) The line y = mx + 8 contains the point (- 4, 4), calculate the value of ‘m’
Solution:
(i) Point (-3, 2) lies on the line ax + 3y + 6 = 0,
Then x = – 3, y = 2 satisfies it
a (-3) + 3(2) + 6 = 0
⇒ -3a + 6 + 6 = 0
⇒ -3a + 12 = 0
⇒ -3a = – 12
⇒ a = 4
(ii) line y = mx + 8 contains the point (-4, 4)
x = – 4, y = 4 satisfies it
4 = m (-4) + 8
⇒ 4 = -4m + 8
⇒ 4m = 8 – 4 = 4
⇒ m = 1
Question 9.
The point P divides the join of (2, 1) and (-3, 6) in the ratio 2 : 3. Does P lie on the line x – 5y + 15 = 0 ?
Solution:
P divides the line joining of the points (2, 1) and (-3, 6) in the ratio of 2 : 3,
co-ordinates of P will be
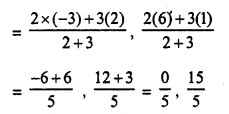
Now, substituting x = 0, y = 3 in the equation
x – 5y + 15 = 0
⇒ 0 – 5 x 3 + 15 = 0
⇒ 0 – 15 + 15 = 0
⇒ 0 = 0 which is true.
Point (0, 3) lies on the line.
Question 10.
The line segment joining the points (5, -4) and (2, 2) is divided by the point Q in the ratio of 1 : 2. Does the line x – 2y = 0 contain Q ?
Solution:
Point Q, divides the line segment joining the points (5, -4) and (2, 2) in the rates of 1 : 2
co-ordinates of Q will be,
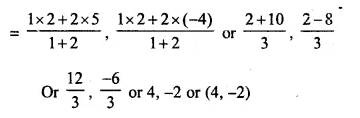
Now, substituting x = 4, y = – 2 in the equation
x – 2y = 0, we get
4 – 2 x (-2) = 0
⇒ 4 + 4 = 0
⇒ 8 = 0 which is not true.
Point Q does not lie on the line x – 2y = 0
Question 11.
Find the point of intersection of the lines : 4x + 3y = 1 and 3x – y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
Solution:
4x + 3y = 1 …..(i)
3x – y = -9 …..(ii).
Multiplying (i) by 1 and (ii) 3
4x + 3y = 1
9x – 3y = -27
Adding, we get-:
1 3x = – 26 ⇒ x = -2
from (ii),
3x – y = – 9
3(-2) – y = -9
⇒ – 6 – y = -9
⇒ -y = -9 + 6 = -3
⇒ y = 3
The point of intersection is (-2, 3)
The line (2k – 1) x – 2y = 4 passes through that point also
It is satisfy it.
(2k – 1) (-2) – 2(3) = 4
⇒ -4k + 2 – 6 = 4
⇒ -4k – 4 = 4
⇒ -4k = 4 + 4 = 8
⇒ k = -2
Hence point of intersection is (-2, 3) and value of k = -2
Question 12.
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Solution:
2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent
They will pass through the same point
Now 2x + 5y = 1 …..(i)
x – 3y = 6 ……(ii)
Multiply (i) by 3 and (ii) by 5, we get :
-6x + 15y = 3
5x – 15y = 30
Adding we get :
11x = 33 ⇒ x = 3
from (ii),
x – 3y = 6
⇒ 3 – 3y = 6
⇒ -3y = 6 – 3 = 3
⇒ y = -1
Point of intersection of first two lines is (3, -1)
Substituting the values in third line x + 5y + 2 = 0
L.H.S. = x + 5y + 2 = 3 + 5(-1) + 2 = 3 – 5 + 2 = 5 – 5 = 0 = R.H.S.
Hence the given three lines are concurrent.
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.