RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C.

Other Exercises

Question 1.
Solution:
In parallelogram ABCD,
Base AB = 32cm
Height DL = 16.5cm.
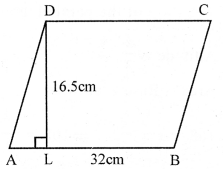
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 1
Area = Base x height = 32 x 16.5 cm² = 528 cm²

Question 2.
Solution:
Base of parallelogram = 1 m 60m = 160 cm
and height = 75 cm
Area = Base x height = 160 x 75 = 12000 cm²
= \(\frac { 12000 }{ 10000 }\) m² = 1.2m²

Question 3.
Solution:
Base of parallelogram = 14dm = 140cm
and height = 6.5 dm = 65cm
Area (in cm²) = Base x height = 140 x 65 = 9100 cm²
Area (in m²) = \(\frac { 140 }{ 100 }\) x \(\frac { 65 }{ 100 }\) = \(\frac { 9100 }{ 10000 }\)
= 0.91 m²

Question 4.
Solution:
Area of parallelogram = 54 cm²
Base = 15 cm
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 2

Question 5.
Solution:
Area of parallelogram ABCD = 153 cm²
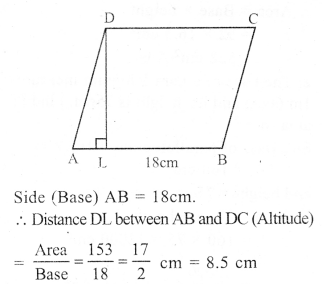
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 3

Question 6.
Solution:
In parallelogram ABCD
AB || DC and AD || BC and AB = DC, AD = BC
AB = DC = 18cm, BC = 12cm
Area of parallelogram ABCD = Base x altitude = DC x AL = 18 x 6.4cm2 = 115.2 cm²
and area of parallelogram ABCD = BC x AM
⇒ 115.2 = 12 x AM
⇒ AM = 9.6 cm

Question 7.
Solution:
In parallelogram ABCD
AB = DC = 15 cm
BC = AD = 8 cm.
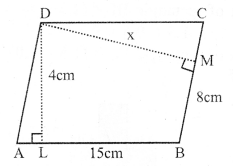
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 4
Distance between longer sides AB and DC is 4cm
i.e. perpendicular DL = 4cm.
DM ⊥ BC.
Area of parallelogram = Base x altitude = AB x DL = 15 x 4 = 60 cm²
Again let DM = x cm
area ABCD = BC x DM = 8 x x = 8x cm²
8x cm² = 60 cm²
⇒ x = 7.5 cm
Distance between shorter lines = 7.5 cm

Question 8.
Solution:
Let Base of the parallelogram = x
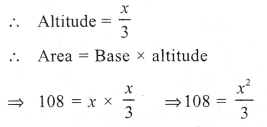
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 5
⇒ x² = 108 x 3 = 324 = (18)²
⇒ x = 18
Base = 18 cm
and altitude = \(\frac { 1 }{ 3 }\) x 18 = 6 cm

Question 9.
Solution:
Area of parallelogram = 512 cm²
Let height of the parallelogram = x
Then base = 2x
Area = Base x height
⇒ 512 = 2x x x
⇒ 2x² = 512
⇒ x² = 256 = (16)²
⇒ x = 16
Base = 2x = 2 x 16 = 32 cm
and height = x = 16 cm

Question 10.
Solution:
(i) Each side of rhombus = 12 cm
height = 7.5 cm
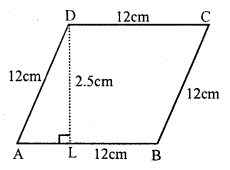
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 6
Area = Base x height = 12 x 7.5 = 90 cm²
(ii) Each side = 2 cm = 20 cm
Height = 12.6 cm
Area = Base x height = 20 x 12.6 = 252 cm²

Question 11.
Solution:
(i) Diagonals of rhombus ABCD are 16 cm and 28 cm
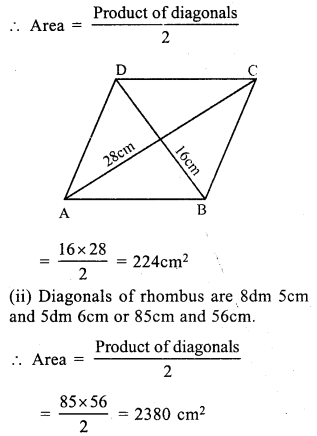
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 7

Question 12.
Solution:
In rhombus ABCD, diagonals AC and BD intersect each other at right angles at O.
AO = OC and BO = OD
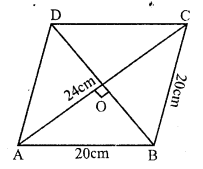
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 8
AO = \(\frac { 1 }{ 2 }\) x AC = \(\frac { 1 }{ 2 }\) x 24 cm = 12cm
Let OB = x
Each side of rhombus = 20cm
In right ∆AOB
AO² + OB² = AB² (Pythagoras Theorem)
⇒ (12)² + OB² = (20)²
⇒ 144 + OB² = 400
⇒ OB² = 400 – 144 = 256 = (16)²
⇒ OB = 16
But BD = 2 BO = 2 x 16 = 32cm
Now, area of rhombus = \(\frac { Product of diagonals }{ 2 }\)
= \(\frac { 24 x 32 }{ 2 }\) cm2 = 384 cm²

Question 13.
Solution:
Area of rhombus = 148.8 cm²
one diagonal = 19.2 cm
Let second diagonal = x
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 9

Question 14.
Solution:
Area of rhombus = 119 cm²
Perimeter = 56 cm
Its side = \(\frac { 56 }{ 4 }\) = 14 cm
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 10

Question 15.
Solution:
Area of rhombus = 441 cm²
Height = 17.5 cm
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 11

Question 16.
Solution:
Base of a triangle = 24.8 cm
Corresponding height = 16.5 cm
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C 12

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.