RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper

by

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper.

Other Exercises

Question 1.
Solution:
We know that all the angles of a rectangle are 90° and the diagonal divides the rectangle into two right angled triangles.
So, one side of the triangle will be 48 m and the diagonal, which is 50 m, will be the hypotenuse.
According to Pythagoras theorem :
(Hypotenuse)² = (Base)² + (Perpendicular)²
Perpendicular
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 1
Other side of the rectangular plot = 14m
Area of the rectangular plot = 48 m x 14 m = 672 m²
Hence, the area of a rectangular plot is 672 m².

Question 2.
Solution:
Length = 9 m; Breadth = 8 m
Height = 6.5 m
Area of the four walls = {2 (l + b) x h} sq. units
= {2 (9 + 8) x 6.5} m² = {34 x 6.5) m² = 221 m²
Area of one door = (2 x 1 .5) m² = 3m²
Area of one window = (1.5 x 1) m² = 1.5 m²
Area of four windows = (4 x 1.5) m² = 6 m²
Total area of one door and four windows = (3 + 6) m² = 9 m²
Area to be painted = (221 – 9) m² = 212 m²
Rate of painting = ₹ 50 per m²
Total cost of painting = ₹ (212 x 50) = ₹ 10,600

Question 3.
Solution:
Given that the diagonal of a square is 64 cm
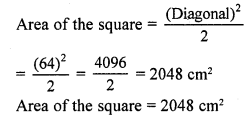
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 2

Question 4.
Solution:
Let ABCD be the square lawn
and PQRS be the outer boundary of the square path
Let one side of the lawn (AB) be x m
Area of the square lawn = x²
Length PQ = (x m + 2 m + 2 m) =(x + 4) m
Area of PQRS = (x + 4)² = (x² + 8x + 16) m²
Now, Area of the path = Area of PQRS – Area of the square lawn
⇒ 136 = x² + 8x + 16x – x²
⇒ 136 = 8x + 16
⇒ 136 – 16 = 8x
⇒ 120 = 8x
⇒ x = 15
Side of the laws = 15 m
Area of the lawn = (Side)² = (15 m)² = 225 m²

Question 5.
Solution:
Let ABCD be the rectangular park
EFGH and IJKL are the two rectangular roads with width 2 m.
Length of the rectangular park AD = 30 cm
Breadth of the rectangular park CD = 20 cm
Area of the road EFGH = 30 m x 2 m = 60 m²
Area of the road IJKL = 20 m x 2m = 40 m²
Clearly, area of MNOP is common to the two roads.
Area of MNOP = 2m x 2m = 4m²
Area of the roads = Area(EFGH) + Area (IJKL) – Area (MNOP)
= (60 + 40) m² – 4 m² = 96 m²

Question 6.
Solution:
Let ABCD be the rhombus whose diagonals intersect at O.
Then, AB = 13 cm
AC = 24 cm
The diagonals of a rhombus bisect each other at right angles.
Therefore, ∆AOB is a right-angled triangle, right angled at O, such that:
OA = \(\frac { 1 }{ 2 }\) AC = 12 cm
AB = 13 cm
By Pythagoras theorem :
(AB)² = (OA)² + (OB)²
⇒ (13)² = (12)² + (OB)²
⇒ (OB)² = (13)² – (12)²
⇒ (OB)2 = 169 – 144 = 25
⇒ (OB)² = (5)²
⇒ OB = 5 cm
BD = 2 x OB = 2 x 5 cm = 10 cm
Area of the rhombus ABCD = \(\frac { 1 }{ 2 }\) x AC x BD cm²
= \(\frac { 1 }{ 2 }\) x 24 x 10
= 120 cm²

Question 7.
Solution:
Let the base of the parallelogram be x m.
The, the altitude of the parallelogram will be 2x m.
It is given that the area of the parallelogram is 338 m².
Area of a parallelogram = Base x Altitude
⇒ 338 = x x 2x
⇒ 338 = 2x²
⇒ x² = 169 m²
⇒ x = 13 m
Base = x m = 13 m
Altitude = 2x m = (2 x 13) m = 26 m

Question 8.
Solution:
Consider ∆ABC Here, ∠B = 90°
AB = 24 cm
AC = 25 cm
Now, AB² + BC² = AC²
BC² = AC² – AB² = (25² – 24²) =(625 – 576) = 49
BC = (√49) cm = 7 cm
Area of ∆ABC = \(\frac { 1 }{ 2 }\) x BC x AB Sq.units
= \(\frac { 1 }{ 2 }\) x 7 x 24 cm² = 84 cm²
Hence, area of the right angled triangle is 84 cm².

Question 9.
Solution:
Radius of the wheel = 35 cm
Circumference of the wheel = 2πr
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 3

Question 10.
Solution:
Let the radius of the circle be r cm
Area = (πr²) cm²
πr² = 616
⇒ \(\frac { 22 }{ 7 }\) x r x r = 616
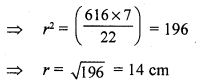
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 4
Hence, the radius of (he given circle is 14 cm.

Mark (✓) against the correct answer in each of the following:
Question 11.
Solution:
(a) 14 cm
Let the radius of the circle be r cm
Then, its area will be (πr²) cm²
πr² = 154
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 5

Question 12.
Solution:
(b) 154 cm²
Let the radius of the circle be r cm.
Circumference = (2πr) cm
(2πr) = 44
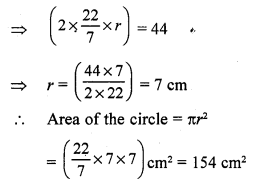
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 6

Question 13.
Solution:
(c) 98 cm²
Given that the diagonal of a square is 14 cm
Area of a square
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 7

Question 14.
Solution:
(b) 10 cm
Given that the area of the square is 50 cm²
We know:
Area of a square
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 8

Question 15.
Solution:
(a) 192 m²
Let the length of the rectangular park be 4x.
Breadth = 3x
Perimeter of the park = 2 (l + b) = 56 m (given)
⇒ 56 = 2 (4x + 3x)
⇒ 56 = 14x
⇒ x = 4
Length = 4x = (4 x 4) = 16 m
Breadth = 3x = (3 x 4) = 12 m
Area of the rectangular park = 16 m x 12 m= 192 m²

Question 16.
Solution:
(a) 84 cm²
Let a = 13 cm, b = 14 cm and c = 15 cm
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 9

Question 17.
Solution:
(a) 16√3 cm²
Given that each side of an equilateral triangle is 8 cm
Area of the equilateral triangle
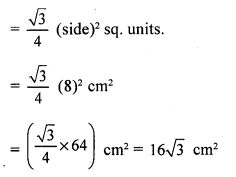
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration CCE Test Paper 10

Question 18.
Solution:
(b) 91 cm²
Base = 14 cm
Height = 6.5 cm
Area of the parallelogram = Base x Height
= (14 x 6.5) cm² = 91 cm²

Question 19.
Solution:
(b) 135 cm²
Area of the rhombus = \(\frac { 1 }{ 2 }\) x (Product of the diagonals)
= \(\frac { 1 }{ 2 }\) x 18 x 15 = 135 cm²
Hence, the area of the rhombus is 135 cm².

Question 20.
Solution:
(i) If d1, and d2 be the diagonals of a rhombus, then its area is \(\frac { 1 }{ 2 }\) d1d2 sq. units.
(ii) If l, b and h be the length, breadth and height respectively of a room, then area of its 4 walls = [2h (l + b)] sq. units.
(iii) 1 hectare = (1000) m². (since 1 hecta metre = 100 m)
1 hectare = (100 x 100) m²
(iv) 1 acre = 100 m².
(v) If each side of a triangle is a cm, then its area = \(\frac {\surd 3 }{ 4 }\) a² cm².

Question 21.
Solution:
(i) False
Area of a triangle = \(\frac { 1 }{ 2 }\) x Base x Height
(ii) True
(iii) False
Area of a circle = πr²
(iv) True

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.