NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 8 |
| Chapter Name | Linear Equations in Two Variables |
| Exercise | Ex 8.2 |
| Number of Questions Solved | 4 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.2
Question 1.
Which one of the following options is true and why? y = 3x + 5 has
(i) a unique solution
(ii) only two solutions
(iii) infinitely many solutions
Solution:
(iii) A linear equation in two variables has infinitely many solutions.
Question 2.
Write four solutions for each of the following equations
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
Solution:
(i) 2x + y = 7
By inspection, x = 2 and y = 3 is a solution because for x = 2, y = 3,
2x + y = 2 x 2 + 3 = 4 + 3 = 7
Now, let us choose x = 0 with this value of x, the given equation reduces to y = 7.
So, x = 0, y = 7 is also a solution of 2x + y = 7. Similarly, taking y = 0,
the given equation reduces to 2x = 7 which has the unique solution x = \(\frac { 7 }{ 2 }\) .
So, x = \(\frac { 7 }{ 2 }\) , y = 0 is a solution of 2x + y = 7.
Finally, let us take x = 1
The given equation now reduces to 2 + y = 7 hose solution is given by y = 5.
Therefore, (1, 5) is also a solution of the given equation.
So, four of the infinitely many solutions of the given equation are (2, 3), (0, 7), ( \(\frac { 7 }{ 2 }\) , 0) and (1,5).
(ii) πx + y = 9
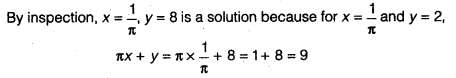
Now, let us choose x = 0 with this value of x,
the given equation reduces to y = 9 which has a unique solution y = 9.
So, x = 0, y = 9 is also a solution of πx + y = 9
Similarly, taking y = 0, the given equation reduces to x = \(\frac { 9 }{ \pi }\) So, x = \(\frac { 9 }{ \pi }\) ,y = 0 is a solution of πx + y = 9as well.
Finally, let us take x = 7 the given equation now reduces to \(\frac { 22 }{ 7 }\) . 7 + y = 9
whose solution is given by y = -13.
Therefore; (7,-13) is also a solution of the given equation.
So, four of the infinitely many solutions of the given equation are
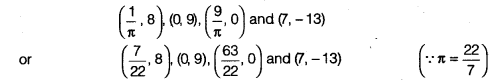
(iii) x = 4y ⇒ x – 4y = 0
By inspection, x = 0, y = 0 is a solution because for x = y = 0, 0 – 4 x 0 = 0 – 0 = 0, it satisfies.
Now, let us choose x = 4 with this value of x,
the given equation reduces to y = 1 which has a unique solution y = 1.
So, x = 4, y = 1 is also a solution , of x – 4y = 0. Similarly, taking y = \(\frac { 1 }{ 2 }\) , the given equation reduces to x = 2.
So , x = 2, y = \(\frac { 1 }{ 2 }\) is a solution x – 4y = 0 as well.
Finally, let us take x = 1, the given equation now reduces to 1 – 4y = 0
whose solution is given by y = \(\frac { 1 }{ 4 }\). Therefore, (1,1/4) is also a solution of the given equation. So, four
of the infinitely many solutions of the given equation are
![]()
Question 3.
Check which of the following are solution of the equation x – 2y = 4 and which are not?
(i) (0, 2)
(ii) (2,0)
(iii) (4,0)
(iv) (√2,4√2)
(v) (1,1)
Solution:
(i) Take x – 2y and put x = 0, y = 2,
we get 0 – 2 x 2 = 0 – 4 = -4 ≠ 4
Hence, (0, 2) is not a solution of x – 2y = 4.
(ii) Take x – 2y and put x = 2, y = 0,
we get 2 – 2 x 0 = 2 – 0 = 2 ≠ 4
Hence, (2, 0) is not a solution of x – 2y = 4.
(iii) Take x – 2y and put x = 4, y = 0;
we get 4 – 2 x 0 = 4 – 0 = 4
Hence, (4, 0) is a solution of x – 2y = 4.
(iv) Take x – 2y and put x = √2, y = 4√2, we get
√2 – 2 x 4√2 = √2 – 8√2 =-7√2 ≠ 4
Hence, (√2,4√2) is not a solution of x – 2y = 4
(v) Take x – 2y and put x = 1, y = 1,
we get 1 – 2 x 1 = 1 – 2 = -1 ≠ 4
Hence, (1,1) is not a solution of x – 2y = 4.
Question 4.
Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3 y = k.
Solution:
Take 2x + 3y = k
Put x = 2, y = 1 then we get, 2 x 2 + 3 x 1 = k
⇒ 4 + 3 = k
⇒ k = 7
We hope the NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.2 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 8 Linear Equations in Two Variables Ex 8.2, drop a comment below and we will get back to you at the earliest.