CBSE Class 9

NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1.

NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1

Question 1.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Given: the ratio of the angles of quadrilateral are 3 : 5 : 9 : 13.
Let the angles of the quadrilateral are 3x, 5x, 9x and 13x.
We know that, sum of angles of a quadrilateral = 360°
∴ 3x + 5x+ 9x+13x = 360°
⇒ 30x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\) = 12°
∴ Angles of the quadrilateral are 3x = 3 x 12 = 36°
5x = 5 x 12 = 60°
9x= 9×12 = 108°
and 13x = 13×12 = 156°

Question 2.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Let given parallelogram is ABCD whose diagonals AC and BD are equal, i.e., AC = BD.
Now, we have to prove that ABCD is a rectangle.

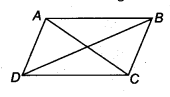
Proof: In ∆ ABC and ∆ DCB, we have
AB = CD (Opposite sides of parallelogram)
BC = CB (Common in both triangles)
and AC = BD (Given)
∴ ∆ABC ≅ ∆DCB (By SSS rule)
∴ ∆ABC = ∠DCB …(i)
(Corresponding Part of Congruent Triangle)
But DC || AB and transversal CB intersect them.
∴ ∠ABC+ ∠DCB = 180°
(∵ Both are interior angles on the same side of the transversal)
⇒ ∠ABC + ∠ABC = 180° [From Eq. (i)]
⇒ 2 ∠ ABC = 180°
⇒ ∠ABC = 90°= ∠DCB
Thus, ABCD is a parallelogram and one of angles is 90°.
Hence, ABCD is a rectangle.
Hence proved.

Question 3.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
Given: a quadrilateral ABCD whose diagonals AC and BD bisect each other at right angles.

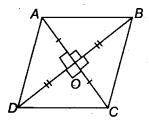
i.e, OA = OC and OB = OD
and ∠AOD = ∠AOB = ∠COD = ∠BOC = 90°
To prove: ABCD is a rhombus.
Proof: In ∆OAB and ∆ODC, we have
OA = OC and OB = OD (Given)
∠AOB = ∠COD (Vertically opposite angles)
∴ ∆OAB ≅ ∆OCD (By SAS rule)
∴ AB = CD ,..(i)
(Corresponding part of congruent triangles)
Again, in ∆OAD and ∆OBC, we have
OA = OC and OD = OB (Given)
and ∠AOD = ∠BOC (Vertically opposite angle)
∴ A OAD = A OCB (By SAS rule)
∴ AD = BC …(ii) (Corresponding part of congruent triangles)
Similarly, we can prove that
AB = AD
CD = BC …(iii)
Hence, from Eqs. (i), (ii) and (iii), we get
AB = BC = AD = CD
Hence, ABCD is a rhombus.
Hence proved.

Question 4.
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Given: A square ABCD whose diagonals AC and BD intersect at O.

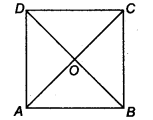
i. e, . AC = BD, OD = OB, OA = OC and AC ⊥ BD
Proof: In A ABC and A BAD, we have
AB = BA (Common)
BC= AD (Sides of a square)
∠ABC = ∠BAD = 90°
∴ ∆ABC ≅ ∆BAD (By SAS rule)
AC = BD
(Corresponding Parts of Congruent Triangle)
∴ ∆OAB and ∆OCD
AB = DC (Sides of a square)
∠ OAB = ∠DCO
(∵ AB || CD and transversal AC intersect)
and ∠ OBA = ∠BDC
(∵AB|| CD and transversal BD intersect)
∴ ∆OAB ≅ ∆OCD
OA = OC and OB = OD
(Corresponding Parts of Congruent Triangle)
Now, in ∆AOB and ∆AOD, we have
OB = OD (Prove in above)
AB = AD (Sides of a square)
AO = OA (Common)
∴ ∆ AOB = ∆AOD (By SSS)
∴ ∠AOB = ∠AOD (By CPCT)
But ∠AOB + ∠AOD-180° (Linear pair)
∴ ∠AOB = ∠AOD = 90°
Thus, AO ⊥ BDi.e.,AC ⊥ BD.
Hence, AC = BD, OA = OC, OB = OD and AC ⊥ BD
Hence proved.

Question 5.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
Given: A quadrilateral ABCD in which AC = BD and AC ⊥ BD such that OA = OC and OB = OD. So, ABCD is a parallelogram.

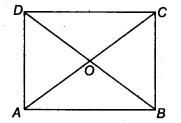
To prove: ABCD is a square.
Proof: Let AC and BD intersect at a point O.
In ∆ABO and ∆ADO, we have
BO = OD (Given)
AO = OA (Common)
∠AOB = ∠AOD = 90° (Given)
∴ ∆ABO ≅ ∆ADO (By SAS)
∴ AB = AD (By CPCT)
and AD = BC (Opposite sides of parallelogram)
∴ AB = BC = DC = AD …(i)
Again, in ∆ABC and ∆BAD, we have
AB = BA (Common)
AC = BD (Given)
BC= AD [From Eq. (i)]
∴ ∆ABC = ∆BAD (By SSS)
∠ABC= ∠ BAD
∠ABC+ ∠ BAD =180° …(ii)
But
∠ABC = ∠ BAD = 180° (Sum of interior angles of a parallelogram)
∴ ∠ABC = ∠BAD = 90° [From Eq. (ii)]
Thus, AB = BC = CD = DA and ∠A = 90°
∴ ABCD is a square.
Hence proved.

Question 6.
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.

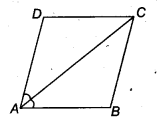
Solution:
Given: diagonal AC of a parallelogram ABCD bisects ∠A

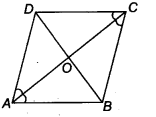
i.e., ∠DCA = ∠ BAC = \(\frac { 1 }{ 2 }\) ∠BAD ….(i)
Here, AB || CD and AC is transversal.
∴ ∠DCA = ∠CAB (Pair of alternate angle)…(ii)
and ∠BCA = ∠ DAC (Pair of alternate angle).. .(iii)
From Eqs. (i), (ii) and (iii), we get
∠DAC = BCA = ∠ BAC = ∠DCA
Now, ∠BCD = ∠BCA + ∠DCA
= ∠DAC + ∠CAB
= ∠BAD
∴ Diagonal AC also bisects ∠C.
Again, in ∆OAD and ∆ OCD, we have
OA = OC (∵ Diagonals bisect each other)
OD = OD (Common)
∴ ∠AOD = ∠ COD = 90°
∴ ∆ OAD ≅ ∆ OCD (By SAS)
∴ AD = CD (By CPCT)
Now AB = CD and AD = BC (Opposite sides of parallelogram)
∴ AB = CD = AD = BC
Hence, ABCD is a rhombus.
Hence proved.

Question 7.
ABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠C and diagonal BD bisects ∠B as well AS ∠D.
Solution:
Given: ABCD is a rhombus

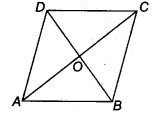
∴ AD = AB = BC = CD ….(i)
To prove:
(i) Diagonal AC bisect ∠A as well as ∠C.
(ii) Diagonal BD bisects ∠B as well as ∠D.
Proof:
(i) Let AC and BD are the diagonals of rhombus ABCD.
In ∆ABC and ∆ADC,
AD = AB
CD = BC [From Eq,(i)]
and AC = CA (Common)
∴ ∆ABC ≅ ∆ADC ( By SSS rule)
∴ ∠DAC = ∠BAC (By CPCT)
and ∠DCA = ∠ BCA
Also, ∠DAC = ∠DCA
and ∠BAC = ∠ BCA
This shows that AC bisect ∠ A as well as ∠C.
(ii) Again, in ∆BDCand ∆BDA,
AB = BC
AD = CD
BD = BD (Common)
∴ ∆ BDC ≅ ∆ BDA (SSS rule)
∴ ∠BDA = ∠BDC
and ∠DBA = ∠DBC
Also, ∠BDA = ∠DBA
and ∠BDC = ∠DBC
This shows that BD bisect ∠B as well as ∠D.

Question 8.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠ B as well as ∠D.
Solution:
Given: ABCD is a rectangle.

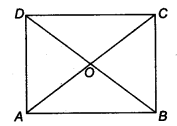
∴ AB = CD and BC= AD …(i)
To Prove (i) ABCD is a square.
i.e., AB = BC = CD = DA
(ii) Dioagonal BDbisects ∠B as well as ∠D.
Proof (i) In ∆ADC and ∆ABC, we have
Since, AB || DC and AC transversal intersect
∠DAC = ∠BAC
∠DCA = ∠BCA
and AC = CA (Common)
∴ ∆ADC ≅ ∆ ABC (By ASA rule)
AD = AB (By CPCT)
and CD = BC …(ii)
Hence, from Eqs. (i) and (ii), we get
AB = BC- AD = CD
∴ ABCD is a square.
(ii) In ∆AOB and ∆COB, we have
AB = BC (Side od square)
BO = OB (Common)
OA = OC
(∵ Diagonal of square bisect each other)
∴ ∆AOB ≅ ∆COB
∴ ∠OBA = ∠OBC
This shows that BO or BD bisect ∠B.
Similarly, in ∆ AOD and ∆ COD, we have
AD = CD (Side od square)
OD = DO (Common)
and OA = OC
(∵ Diagonal of square bisect each other)
∴ ∆ AOD ≅ ∆ COD (By ASA rule)
∴ ∠ADO = ∠CDO
This shows that DO or DB bisect ∠D.
Hence proved.

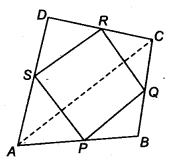
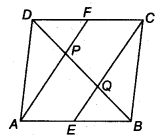
Question 9.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that

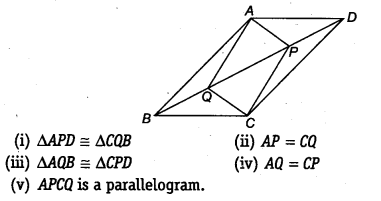
Solution:
Given: ABCD is a parallelogram and P and Q are lie on BD such that

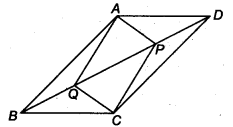
DP = PQ ….(i)
(i) We have to show,
∆APD ≅ ∆CQB
Now, in ∆APD and ∆CQB, we have
DP = BQ (Given)
AD = BC
(Opposite sides are equal in parallelogram)
∵ AD || BC and BD is a transversal.
∴ ∠ADP = ∠QBC (Alternate interior angle)
∴ ∆APD ≅ ∆CQB (By SAS)
(ii) Since, ∆APD ≅ ∆CQB
∴ AP = CQ
(iii) Here, we have to show, ∆AQB ≅ ∆CPD
Now, in ∆AQB and ∆CPD, we have
BQ = DP (Given)
AB = CD (Opposite sides of parallelogram)
∵ AB || CD and BD is a transversal.
∴ ∠ABQ = ∠CDP (Alternate interior angle)
∴ ∆AQB s ∆ CPD
(iv) Since, ∆AQB ≅ ∆CPD
∴ AQ = CP
(v) Now, in ∆APQ and ∆PCQ, we have
AQ = CP [From part (iv)]
AP = CQ [From part (ii)]
PQ = QP (Common)
∴ ∆APQ = ∆PCQ (By SSS)
∴ ∠APQ = ∠PQC
and ∠AQP = ∠CPQ (Vertically opposite)
Now, these equal angles form a pair of alternate angle when line segment AP and QC are intersected by a transversal PQ.
∴ AP || CQ and AQ || CP
Now, both pairs of opposite sides of quadrilateral APCQ are parallel.
Hence, APCQ is a parallelogram.
Hence proved.

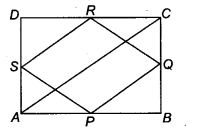
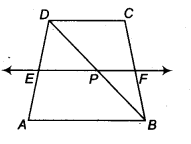
Question 10.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see figure). Show that

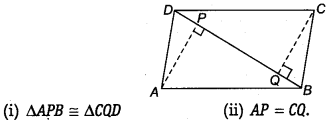
Solution:
Given: ABCD is a parallelogram and AP and CQ are perpendicular from vertices A and C on diagonal BD.
∵ AB || CD and BD is a transversal.
∴ ∠CDB = ∠DBA …(i)
(i) Now, in ∆ APB and ∆ CQD, we have
CD = AB (Sides of parallelogram)
∠CQD = ∠APB = 90° (Given)
∠CDQ = ∠ABP [From Eq. (i)]
∴ ∆APB ≅ ∆CQD (By ASA rule)
(ii) ∵ ∆APB ≅ ∆CQU (By CPCT)
∴ AP = CQ
Hence proved.

Question 11.
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC – EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F, respectively (see figure).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram

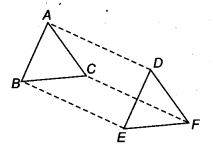
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
Solution:
Given: in ∆ABC and ∆DEF,
AB = DE, AB || DE
and BC = EF,BC||EF

(i) Now, in quadrilateral ABED,
AB = DE and AB || DE (Given)
⇒ ABED is a parallelogram.
(∵ A pair of opposite sides is equal and parallel)

(ii) In quadrilateral BEFC,
BC = EF and BC || EF.
⇒ BEFC is a parallelogram.
(∵ A pair of opposite sides is equal and parallel)

(iii) Since, ABED is a parallelogram.
∴ AD || BE and AD = BE …(i)
Also, BEFC in a parallelogram.
∴ CF || BE and CF = BE …(ii)
From Eqs. (i) and (ii), we get
AD || CF and AD =CF

(iv) In quadrilateral ACFD, we have
AD || CF and AD = CF [From part (iii)]
⇒ ACFD is a parallelogram.

(v) Since, ACFD is a parallelogram.
∴ AC = DF and AC || DF

(vi) Now, in ∆ABC and ∆DEF,
AB = DE (Given)
BC = EE (Given)
and AC = DF [From part (v)]
∴ ∆ABC ≅ ∆DEF (By SSS rule)

Question 12.
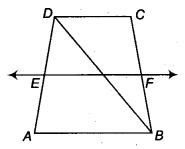
ABCD is a trape∠ium in which AB || CD and AD = BC (see figure). Show that
(i )∠A=∠B
(ii )∠C=∠D
(iii) ∆ABC ≅ ∆BAD
(iv) diagonal AC = diagonal BD

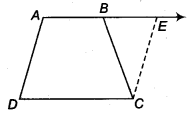
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E].
Solution:
Given: ABCD is a trapezium.

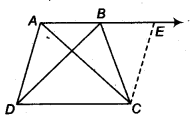
AB || CD and AD = BC
Now, extend AB and draw a line through C parallel to DA intersecting AB produced at E.
Now, ADCE is a parallelogram.
∴ AD || CE and AD = CE
But AD = BC
∴ AD = BC = CE

(i) We know that, ∠A + ∠E = 180°
(∵ Interior angles on the same side of the transversal AE)
⇒ ∠E = 180° – ∠A
Since, BC = EC
∴ ∠E = ∠CBE = 180° – ∠A
Also, ∠ ABC =180° – ∠CBE (∵ ABE is straight line)
= 180°- 180°+ ∠A
⇒ ∠B = ∠A …(i)

(ii) Now ∠A+ ∠D = 180°
(∵ Interior angles on the same side of the transversal AD)
⇒ ∠D=180°-∠A
⇒ ∠D = 180° -∠B [From Eq. (i)]…(ii)
Also, ∠C+ ∠B = 180°
(∵ Interior angles on the same side of the transversal BC)
⇒ ∠C = 180°-∠B …..(iii)
From Eqs. (ii) and (iii), we get
∠C = ∠D

(iii) Now, in ∆ABC and ∆ BAD, we have
AB = BA (Common)
AD = BC (Given)
∠A=∠B [From Eq. (i)]
∴ ∆ABC ≅ ∆ BAD (By SAS)

(iv) Since, ∆ABC ≅ ∆BAD
∴ AC = BD
Hence proved.
We hope the NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2.

NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2

Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that
(i) SR || AC and SR = \(\frac { 1 }{ 2 }\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

Solution:
Given: P, Q, Ft and S are mid-points of the sides.
∴ AP = PB, BQ = CQ
CR = DR and AS = DS
(i) In ∆ADC, we have
S is mid-point of AD and R is mid-point of the DC.
We know that, the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
∴ SB || AC …(i)
Also , SR = \(\frac { 1 }{ 2 }\) AC …(ii)
(ii) Similarly, in ∆ABC, we have
PQ || AC ….(iii)
and PQ = \(\frac { 1 }{ 2 }\) AC ….(iv)
Now, from Eqs. (i) and (iii), we get
SR = \(\frac { 1 }{ 2 }\) AC …..(v)
(iii) Now, from Eqs. (i) and (iii), we get
PQ || SR
and from Eq. (v), PQ = SR
Since, a pair of opposite sides of a quadrilateral PQRS is equal and parallel.
So, PQRS is a parallelogram.
Hence proved.

Question 2.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: ABCD is a rhombus and P, Q, R and S are mid-points of AB, BC, CD and DA

By mid-point theorem,

∴ PQRS is a parallelogram.
Now, we know that diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF = 90°
Now, RQ || BD (By mid-point theorem)
⇒ RE || OF
Also, SP|| AC [From Eq. (i)]
⇒ FR || OE
∴ OERF is a parallelogram.
So, ∠ ERF = ∠EOF = 90°
(Opposite angle of a quadrilateral is equal)
Thus, PQRS is a parallelogram with ∠R = 90°
Hence, PQRS is a rectangle.

Question 3.
ABCD is a rectangle and P, Q, R ans S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: ABCD is a rectangle.

∴ ∠A = ∠B = ∠C= ∠D = 90°
and AD = BC, AB = CD
Also, given P, Q, R and S are mid-points of AB, BC, CD and DA .respectively.
∴ PQ || BD and PQ = \(\frac { 1 }{ 2 }\) BD
In rectangle ABCD,
AC = BD
∴ PQ = SR …(ii)
Now, in ∆ASP and ∆BQP
AP = BP (Given)
AS = BQ (Given)
∠A = ∠B (Given)
∴ ∆ASP ≅ ∆BQP (By SAS)
∴ SP = PQ (By CPCT)…(ii)
Similarly, in ∆RDS and ∆RCQ,
SD = CQ (Given)
DR = RC (Given)
∠C=∠D (Given)
∴ ∆RDS ≅ ∆RCQ (By SAS)
∴ SR = RQ (By CPCT)…(iii)
From Eqs. (i), (ii) and (iii), it is clear that quadrilateral PQRS is a rhombus.

Question 4.
ABCD is a trapezium in which AB | | DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.

Solution:
Given: ABCD is a trapezium in which AB || CD and E is mid-point of AD and EF || AB.
In ∆ABD, we have
EP\\AB

and E is mid-point of AD.
So, by theorem, if a line drawn through the mid-point of one side of a triangle parallel to another side bisect the third side.
∴ P is mid-point of BD.
Similarly, in ∆ BCD, we have,
PF || CD (Given)
and P is mid-point of BD.
So, by converse of mid-point theorem, F is mid-point of CB.

Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.

Solution:
Given: ABCD is a parallelogram and E, F are the mid-points of sides AB and CD respectively.
To prove: Line segments AF and EC trisect the diagonal BD.
Proof: Since, ABCD is a parallelogram.
AB || DC
and AB = DC (Opposite sides of a parallelogram)
⇒ AE || FC and \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) DC
⇒ AF || FC and AF = FC
∴ AECF is a parallelogram.
∴ AF || FC
⇒ EQ || AP and FP || CQ
In ∆ BAP, E is the mid-point of AB and EQ || AP, so Q is the mid-point of BP.
(By converse of mid-point theorem)
∴ BQ = PQ ….(i)
Again, in ∆DQC, F is the mid-point of DC and FP || CQ, so P is the mid-point of DQ. (By converse of mid-point theorem)
∴ QP = DP …(ii)
From Eqs. (i) and (ii), we get
BQ = PQ = PD
Hence, CE and AF trisect the diagonal BD.

Question 6.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
Let ABCD is a quadrilateral and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively, i.e., AS = SD, AP = BP, BQ = CQ and CR = DR. We have to show that PR and SQ bisect each other i.e., SO = OQ and PO = OR.

Now, in ∆ADC, S and R are mid-points of AD and CD.
We know that, the line segment joining the mid-points of two sides of a triangle is parallel to the third side. (By mid-point theorem)
∴ SR || AC and SR = \(\frac { 1 }{ 2 }\) AC …(i)
Similarly, in ∆ ABC, P and Q are mid-points of AB and BC.
∴ PQ || AC and PQ = \(\frac { 1 }{ 2 }\) AC (By mid-point theorem)…(ii)
From Eqs. (i) and (ii), we get
PQ || SR
and PQ = SR = \(\frac { 1 }{ 2 }\) AC
∴ Quadrilateral PQRS is a parallelogram whose diagonals are SQ and PR. Also, we know that diagonals of a parallelogram bisect each other. So, SQ and PR bisect each other.

Question 7.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac { 1 }{ 2 }\) AB
Solution:
Given: ABC is a right angled triangle.
∠C = 90°

and M is the mid-point of AB.
Also, DM || BC
(i) In ∆ ABC, BC || MD and M is mid-point of AB.
∴ D is the mid-point of AC. (By converse of mid-point theorem)
(ii) Since, MD || BC and CD is transversal
∴ ∠ADM = ∠ACB (Corresponding angles)
But ∠ACB = 90°
∴ ∠ADM = 90° ⇒ MD ⊥ AC
(iii) Now, in ∆ ADM and ∆ CDM, we have
DM = MD (Common)
AD = CD (∵ D is mid point of AC)
∴ ∠ADM = ∠MDC (Each equal to 90°)
∴ ∆ ADM = ∆ CDM (By SAS)
∴ CM = AM (By CPCT)…(i)
Also, M is mid-point of AB.
∴ AM – BM = \(\frac { 1 }{ 2 }\) AB ….(ii)
From Eqs. (i) and (ii), we get
CM = AM = \(\frac { 1 }{ 2 }\) AB
Hence proved.
We hope the NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2, drop a comment below and we will get back to you at the earliest.