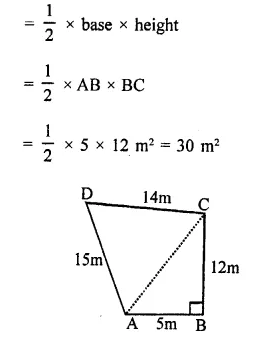
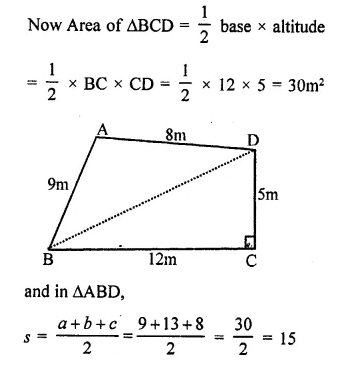
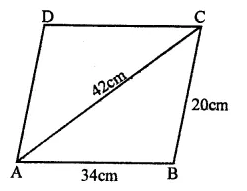
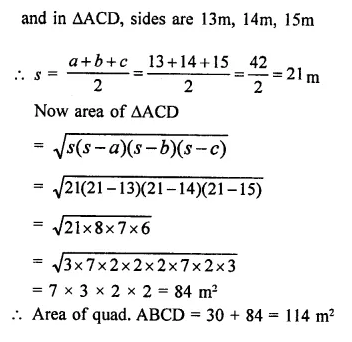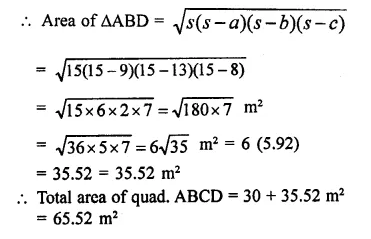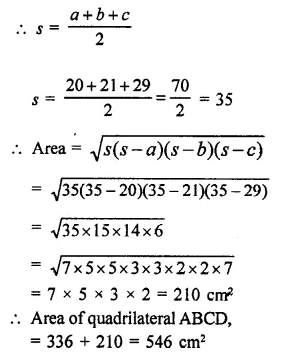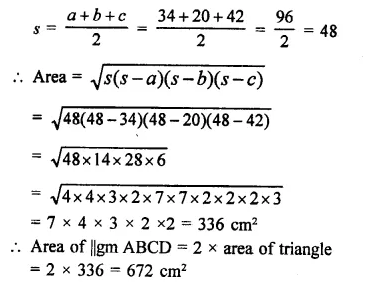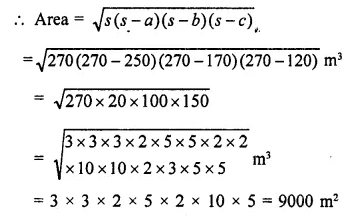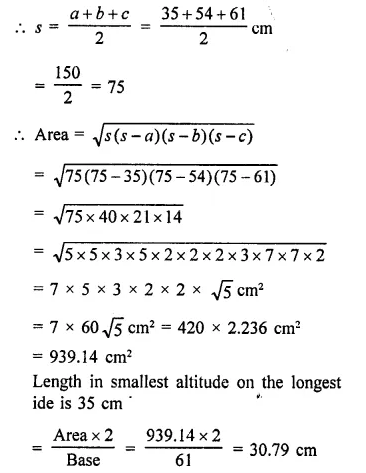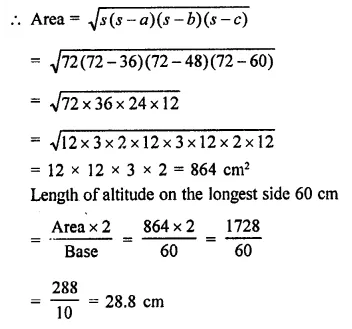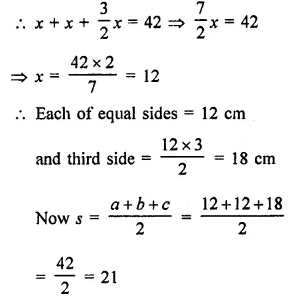NCERT Solutions for Class 9 Science Chapter 10 Gravitation
These Solutions are part of NCERT Solutions for Class 9 Science. Here we have given NCERT Solutions for Class 9 Science Chapter 10 Gravitation. LearnInsta.com provides you the Free PDF download of NCERT Solutions for Class 9 Science (Physics) Chapter 10 – Gravitation solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 10 – Gravitation Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks.
More Resources
- NCERT Solutions for Class 9 Science
- HOTS Questions for Class 9 Science
- Value Based Questions in Science for Class 9
- NCERT Exemplar Solutions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
NCERT TEXT BOOK QUESTIONS
IN TEXT QUESTIONS
Question 1.
State the universal law of gravitation. (CBSE Sample Paper, CBSE 2010, 2011, 2012, 2013, 2015)
Answer:
The force of attraction between two particles or objects is
- directly proportional to the product of the masses of the objects and
- inversely proportional to the square of the distance between them.
Question 2.
Write the formula to find the magnitude of the gravitational force between the earth and an object on
the surface of the earth. (CBSE 2011, 2012, 2013)
Answer:
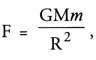
where M = mass of the earth, m = mass of the object, R = radius of the earth.
Question 3.
What do you mean by free fall ?
Or
What is meant by free fall ? (CBSE 2010, 2011, 2012, 2013)
Answer:
When an object falls towards the earth under the influence of gravitational force alone, then the object is in free fall.
Question 4.
What do you mean by acceleration due to gravity ? (CBSE 2011, 2012, 2013)
Answer:
The acceleration with which an object falls freely towards the earth is known as acceleration due to gravity. It is denoted by ‘g’.
Question 5.
What is the difference between the mass of an object and its weight ?
(CBSE 2010, 2011, 2012, 2013)
Answer:
| Mass | Weight |
| The quantity of matter contained in a body is called the mass of the body. | The force with which the earth attracts a body towards its centre is called the weight of the body. |
| Mass of a body remains constant. | Weight of a body changes from place to place as it depends on the value ‘g’ and ‘g’ is different at different places. |
| Mass of a body is never zero. | Weight of a body at the centre of the earth is zero. |
| Mass is a scalar quantity. | Weight is a vector quantity. |
| Mass is measured in kg. | Weight is measured in kg wt or N. |
| Mass is measured by a beam balance. | Weight is measured by a weighing machine or a spring balance. |
Question 6.
Why is the weight of an object on the moon 1/6 th its weight on the earth ?
Answer:
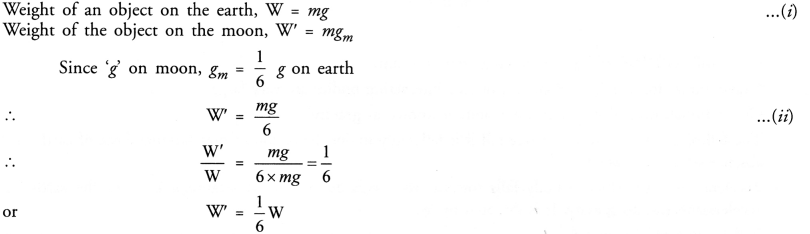
Question 7.
You find your mass to be 42 kg on a weighing machine. Is your mass more or less than 42 kg ?
Answer:
Weighing machine gives the weight of an object.
Weight = Mass x g
![]()
Thus, mass is less than the weight.
NCERT CHAPTER END EXERCISE
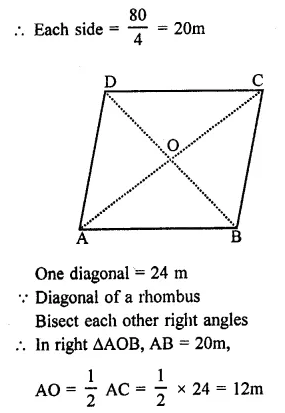
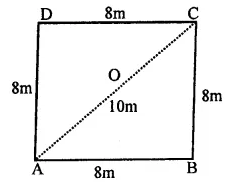
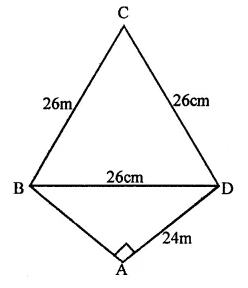
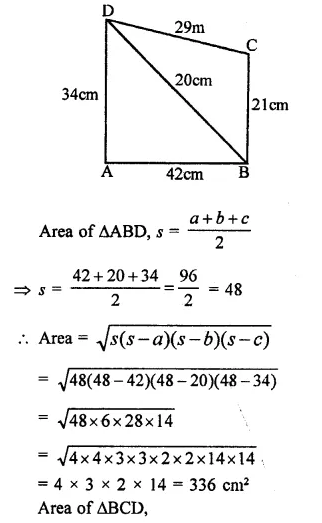
Question 1.
How does the force of gravitation between two objects change when the distance between them is reduced to half ? (CBSE 2011)
Answer:
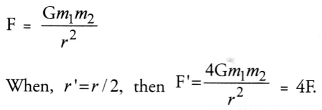
Thus, the force of gravitation becomes 4 times its original value.
Question 2.
Gravitational force acts on all objects in proportion to their masses. Why, then, a heavy object does not fall faster than a light object ? (CBSE 2015)
Answer:
The acceleration with which a body falls towards the earth is constant (= 9.8 m s-2) and independent of the mass of the body. Thus, all bodies fall with the same acceleration irrespective of their masses. That is why, a heavy body does not fall faster than the light body.
Question 3.
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface ?Mass of the earth is 6 x 1024 kg and radius of earth is 6.4 x 106 m.
Answer:
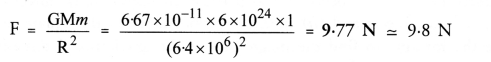
Question 4.
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth ? Why ?
Answer:
Gravitational force with which a body A attracts another body B is equal in magnitude and opposite in direction to the gravitational force with which a body B attracts the body A. Thus, the magnitude of force with which the earth attracts the moon is equal to the magnitude of the force with which the moon attracts the earth. Thus, both the earth and the moon attract each other with equal forces.
Question 5.
If the moon attracts the earth, why does the earth not move towards the moon ?
(CBSE 2011, 2013, 2015)
Answer:.
The acceleration produced in the earth due to the force exerted on it by the moon is very small as the mass of the earth is very large. Hence, the movement of the earth towards the moon is not noticed.
Question 6.
What happens to the force between two objects, if
- the mass of one object is doubled ?
- the distance between the objects is doubled and tripled ?
- the masses of both the objects are doubled ? (CBSE 2011, 2013, 2014)
Answer:
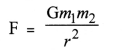
- F is doubled if m1 or m2 is doubled.
- F becomes 1/4 times the original value if distance (r) is doubled and F becomes 1/9 times the original value if r is tripled.
- F becomes four times the original value if both m1 and m2 are doubled.
Question 7.
What is the importance of universal law of gravitation ?
Answer:
The gravitational force plays an important role in nature
- All the planets revolve around the sun due to the gravitational force between the sun and the planets. The force required by a planet to move around the sun in elliptical path (known as centripetal force) is provided by the gravitational force of attraction between the planet and the sun. Thus, gravitational force is responsible for the existence of the solar system.
- Tides in oceans are formed due to the gravitational force between the moon and the water in oceans.
- Gravitational force between a planet and its satellite (i.e., moon) decides whether a planet has a moon or not. Since the gravitational force of the planets like mercury and venus is very small, therefore, these planets do not have any satellite or moon.
- Artificial and natural satellites revolve around the earth due to the gravitational force between the earth and the satellite. The gravitational force between the earth and the satellite provides a necessary centripetal force to the satellite to move in a circular path around the earth.
- The atmosphere (envelope of gases) of the earth is possible due to gravitational force of the earth.
- Rainfall and snowfall is possible only due to gravitational force of the earth.
- We stay on the earth due to the gravitational force between the earth and us.
Question 8.
What is the acceleration of free fall ?
Answer:
Acceleration of free fall = 9.8 m s-2 ≈ 10 m s-2.
Question 9.
What do we call the gravitational force between the earth and an object ?
Answer:
Force of gravity.
Question 10..
Amit buys few grams of gold at the poles as per the instruction of one of his friends. He hands over the same when he meets him at the equator. Will the friend agree with the weight of gold bought ? If not, why ? (Hint: The value of g is greater at the poles than at the equator) (CBSE 2012, 2013)
Answer:
Weight = mg
Since value of g is greater at the poles than at the equator, so the weight of gold at the poles will be greater than the weight of gold at the equator. Hence, his friend will say that the weight of the gold is less than as told by Amit.
Question 11.
Why will a sheet of paper fall slower than one that is crumpled into a ball ?
Answer:
Since the area of a sheet of paper is more than the area of the paper crumpled into a small, therefore, a sheet of paper will experience a large opposing force due to air than the ball, while falling down. Hence, a sheet of paper falls slower than one that is crumpled into a ball.
Question 12.
Gravitational force on the surface of the moon is only 1/6 as strong as gravitational force on the earth.
Or
What is the weight in newtons of a 10 kg object on the moon and on the earth ?
Answer:
![]()
Question 13.
A ball is thrown vertically upwards with a velocity of 49 m/s. Calculate
(i) the maximum height to which it rises,
(ii) the total time it takes to return to the surface of the earth.
(CBSE 2011, 2013, 2014)
Answer:

The ball takes the same time to reach the ground from maximum height as time of ascent is equal to time of desent.
Total time taken = 5 s + 5 s = 10 s.
Question 14.
A stone is released from the top of a tower of height 19.6 m. Calculate its final velocity just before touching the ground. (CBSE 2011, 2013)
Answer:
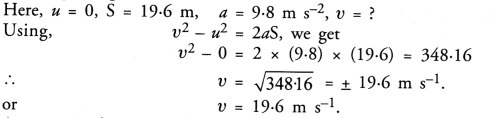
Question 15.
A stone is thrown vertically upward with an initial velocity of 40 m/s and is caught back. Taking g = 10 m/s2, find the maximum height reached by the stone. What is the net displacement and the total distance covered by the stone ?
(CBSE Sample Paper 2010; CBSE 2011, 2012, 2013)
Answer:
Here, u = 40 m/s,
g = -10 m/s2 (sign convention) v = 0 (at the maximum height)
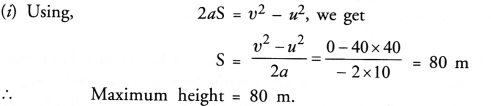
(ii) The stone after reaching the maximum height falls down and reach the ground.
∴ Displacement of the stone = 0
and distance covered by the stone = 80 m + 80 m = 160 m.
Question 16.
Calculate the force of gravitation between the earth and the sun, given that the mass of the earth = 6 x 1024 kg and of the sun = 2 x 1030 kg.
Answer:
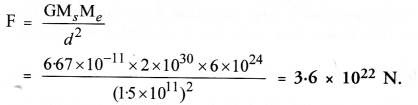
Question 17.
A stone is allowed to fall from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/s. Calculate when and where the two stones will meet ?
Answer:
Let t = time after which both stones meet .
S = distance of the stone dropped from the top of tower
(100 – S) = distance travelled by the projected stone.
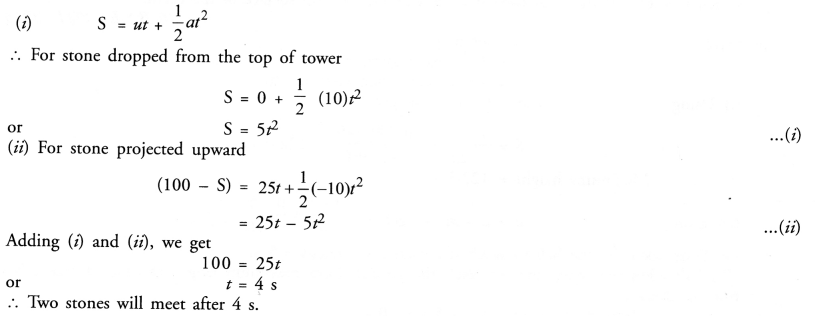
(iii) Put value of t = 4 s in equation (i),
S = 5 x 16 = 80 m
Thus, both the stones will meet at a distance of 80 m from the top of tower.
Question 18.
A ball thrown up vertically returns to the thrower after 6 s. Find
(a) the velocity with which it was thrown up,
(b) the maximum height it reaches, and
(c) its position after 4 s. (CBSE 2011)
Answer:

NCERT Solutions for Class 9 Science Chapter 10 Gravitation
Hope given NCERT Solutions for Class 9 Science Chapter 10 are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.