CBSE Class 7

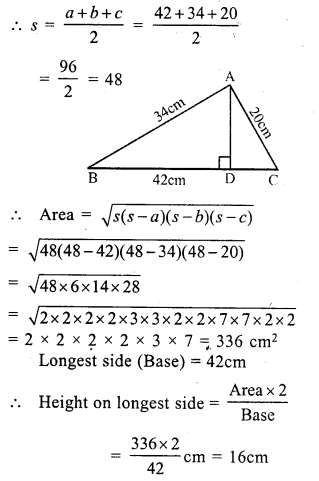
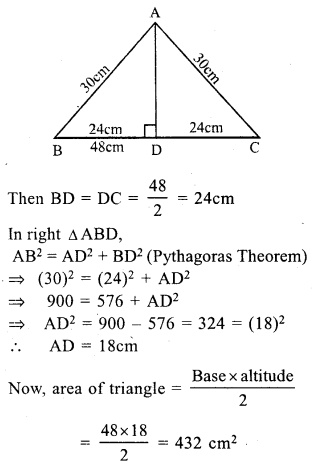
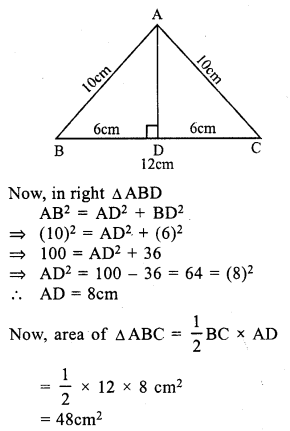
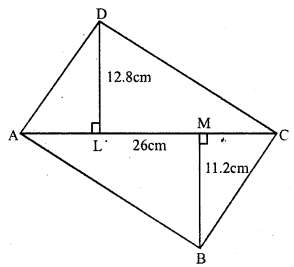
RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20E

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
Radius of the circle (r) = 28 cm

Question 2.
Solution:
(i) Diameter of circle (d) = 35 cm

Question 3.
Solution:
Radius of a circle = 15 cm

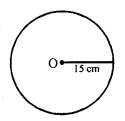
Circumference = 2πr = 2 x 3.14 x 15 = 94.20 cm = 94.2 cm

Question 4.
Solution:
Circumference of a circle (c) = 57.2 cm

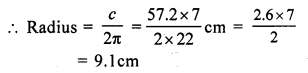
Question 5.
Solution:
Circumference (c) = 63.8 m

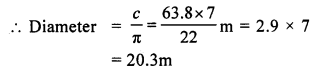
Question 6.
Solution:
Let c be the circumference and d be the diameter of the circle.
c = d + 30
⇒ dπ = d + 30
⇒ dπ – d = 30
⇒ d (π – 1) = 30

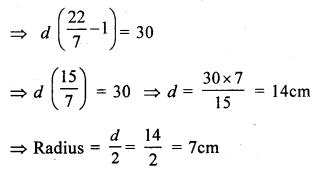
Question 7.
Solution:
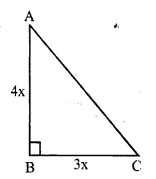
The ratio of the radii of the circles = 5 : 3
Let radius of first circle = 5x
and radius of second circle = 3x
Circumference of first circle = 2πr = 2π x 5x = 10πx
and circumference of second circle = 2π x 3x = 6πx
Ratio = 10πx : 6πx = 10 : 6 = 5 : 3

Question 8.
Solution:
Radius of circular field (r) = 21 m
Circumference = 2πr

Question 9.
Solution:
Outer circumference = 616 m

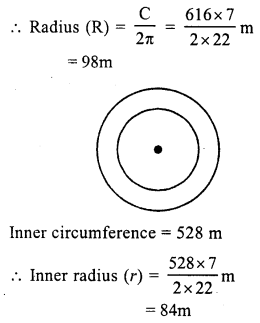
Width of track = R – r = 98 – 84 = 14m

Question 10.
Solution:
Inner circumference of the circular track = 330 m

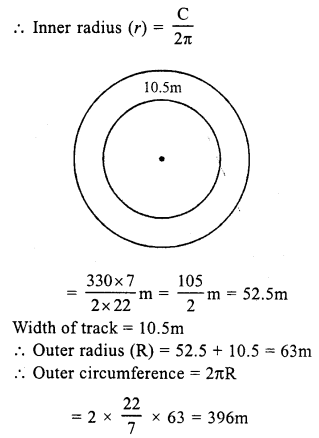
Rate of fencing = Rs. 20 per metre
Total cost = Rs. 20 x 396 = Rs. 7920

Question 11.
Solution:
Radius of inner circle (r) = 98 cm
Inner circumference = 2πr = 2 x \(\frac { 22 }{ 7 }\) x 98 cm = 616 cm

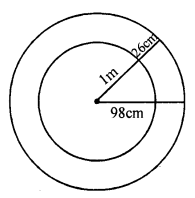
Radius of the outer circle (R) = 1 m 26cm = 126 cm
Outer circumference = 2πR = 2 x \(\frac { 22 }{ 7 }\) x 126 cm = 792 cm

Question 12.
Solution:
Side of equilateral triangle = 8.8 cm
Its perimeter = 8.8 x 3 = 26.4 cm
By bending their wire into a circular shape,
the circumference = 26.4 cm
Let d be the diameter,
Then C = dπ

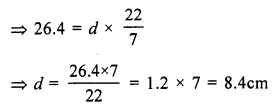
Question 13.
Solution:
Each side of rhombus = 33 cm
Perimeter = 4 x 33 = 132 cm
Perimeter of circle = 132 cm
Let r be the radius

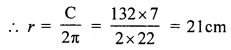
Question 14.
Solution:
Length of rectangle (l) = 18.7 cm
Breadth (b) = 14.3 cm
Perimeter = 2 (l + b) = 2 (18.7 + 14.3) cm = 2 x 33 = 66 cm
Circumference of the so formed circle = 66 cm

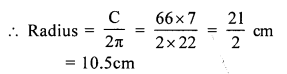
Question 15.
Solution:
Radius of the circle (r) = 35 cm
Its circumference (c) = 2πr

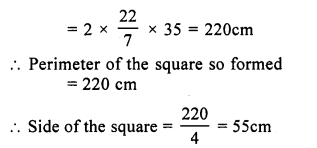
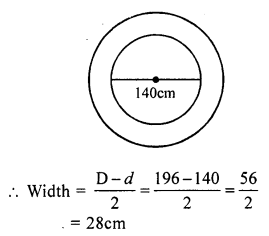
Question 16.
Solution:
Diameter of well (d) = 140 cm
Outer circumference of parapet = 616 cm
Let D be the diameter, then

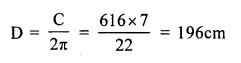
Question 17.
Solution:
Diameter of wheel (d) = 98 cm

Question 18.
Solution:
Diameter of cycle wheel (d) = 70 cm

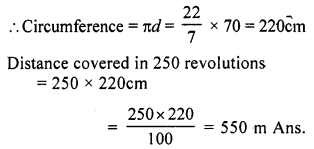
Question 19.
Solution:
Diameter of car wheel (d) = 77 cm
Circumference = πd = \(\frac { 22 }{ 7 }\) x 77 cm

Question 20.
Solution:
No. of revolutions = 5000
Distance covered = 11 km = 11 x 1000 = 11000 m

Question 21.
Solution:
Length of hour hand (r) = 4.2 cm
and length of minutes hand (R) = 7cm

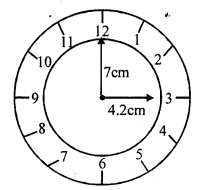
Distance covered by hour hand in 24 hours = 2πR
= 2 x \(\frac { 22 }{ 7 }\) x 4.2
= 26.4 cm
But distance covered by minute hand in one hour = 2πR = 2 x \(\frac { 22 }{ 7 }\) x 7 = 44 cm
and distance covered by minute hand in 24 hours = 44 x 24 cm = 1056 cm
Sum of distance covered by these hands = 26.4 + 1056 = 1082.4 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20D

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
(i) Base of the triangle = 42 cm

Height = 25 cm
Area = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x 42 x 25 = 525 cm²
(ii) Base of the triangle = 16.8 m
and height = 75 cm = 0.75 m
Area = \(\frac { 1 }{ 2 }\) x Base x height
= \(\frac { 1 }{ 2 }\) x 16.8 x 0.75 m2 = 6.3 m²
(iii) Base of a triangle (b) = 8 m = 80 cm
and height (h) = 35 cm
Area = \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) x 80 x 35 = 1400 cm²

Question 2.
Solution:
Base of triangle = 16 cm
area of the triangle = 72 cm²

Question 3.
Solution:
Area of triangular region = 224 m²
Base = 28 m

Question 4.
Solution:
Area of triangle = 90 cm²
and height (h) = 12 cm

Question 5.
Solution:
Let height of a triangular field = x m
Then base (b) = 3x m
and area = \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) x 3x x x

Question 6.
Solution:
Area of the right angled triangle = 129.5 cm²

Question 7.
Solution:
In right angled ∆ABC,
Base BC = 1.2 m

and hypotenuse AC = 3.7 m
But AC² = AB² + BC² (Pythagoras Theorem)
⇒ (3.7)² = AB² + (1.2)²
⇒ 13.69 = AB² + 1.44
⇒ AB² = 13.69 – 1.44
⇒ AB² = 12.25 = (3.5)²
⇒ AB = 3.5 m
Now, area of ∆ABC = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x 1.2 x 3.5 m² = 2.1 m²

Question 8.
Solution:
Legs of a right angled triangle = 3 : 4
Let one leg (base) = 3x

Then second leg (altitude) = 4x
Area = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x 3x x 4x = 6x²
6x² = 1014
⇒ x² = \(\frac { 1014 }{ 6 }\) = 169 = (13)²
x = 13
one leg'(Base) = 3x = 3 x 13 = 39 cm
and second leg (altitude) = 4x = 4 x 13 = 52 cm

Question 9.
Solution:
One side BC of a right triangular scarf = 80 cm

and longest side AC = 1 m = 100 cm
By Pythagoras Theorem,
AC² = AB² + BC²
⇒ (100)² = AB² + (80)²
⇒ 10000 = AB² + 6400
⇒ AB² = 10000 – 6400
⇒ AB² = 3600 = (60)²
⇒ AB = 60
Second side = 60 cm
Area of the scarf = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 80 x 60 cm2 = 2400 cm²
Rate of cost = Rs. 250 per m²
Total cost =\(\frac { 2400 }{ 100 x 100 }\) x 250 = Rs. 60

Question 10.
Solution:
(i) Side of the equilateral triangle (a) = 18 cm

Question 11.
Solution:
Area of equilateral triangle = 16√3 cm²
Let each side = a
then \(\frac { \surd 3 }{ 4 }\) a² = 16√3
⇒ a² = \(\frac { 16\surd 3\times 4 }{ \surd 3 }\)
⇒ a² = 64 = (8)²
a = 8 cm
Each side = 8 cm

Question 12.
Solution:
Each side of an equilateral triangle = 24cm
Length of altitude = \(\frac { \surd 3 }{ 2 }\) a = \(\frac { \surd 3 }{ 2 }\) x 24
= 12√3 cm = 12 (1.73) = 20.76 cm

Question 13.
Solution:
(i) a = 13 m, b = 14 m, c = 15 m

= 2 x 2 x 3 x 7 x 7 x 7 = 4116 m²

Question 14.
Solution:
Let a = 33 cm, b = 44 cm, c = 55 cm

Question 15.
Solution:
Perimeter of the triangle = 84 cm
Ratio in side = 13 : 14 : 15
Sum of ratios =13 + 14 + 15 = 42
Let then first side = \(\frac { 84 x 13 }{ 42 }\) = 26 cm

Question 16.
Solution:
Let a = 42 cm, b = 34 cm, c = 20 cm

Question 17.
Solution:
In isosceles ∆ABC
Base BC = 48 cm.
and AB = AC = 30cm.
Let AD ⊥ BC

Question 18.
Solution:
Perimeter of an isosceles triangle = 32 cm
Base = 12 cm
Sum of two equal sides = 32 – 12 = 20 cm
Length of each equal side = \(\frac { 20 }{ 2 }\) = 10cm
Let AD ⊥ BC
BD = DC = \(\frac { 12 }{ 2 }\) = 6 cm

Question 19.
Solution:
In quadrilateral ABCD,
diagonal AC = 26 cm.

and perpendiculars DL = 12.8cm, BM = 11.2 cm
Area of quadrilateral ABCD
= \(\frac { 1 }{ 2 }\) (Sum of perpendicular) x diagonal
= \(\frac { 1 }{ 2 }\) (12.8 + 11.2) x 26 cm²
= \(\frac { 1 }{ 2 }\) x 24 x 26 = 312 cm²

Question 20.
Solution:
In quad. ABCD,
AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm
and diagonal AC = 30 cm
In ∆ABC,

Question 21.
Solution:
ABCD is a rectangle in which AB = 36 m
and BC = 24m
In ∆AED,
EF = 15 m
AD = BC = 24 m.
Now area of rectangle ABCD = l x b = 36 x 24 cm² = 864 cm²
Area of ∆AED = \(\frac { 1 }{ 2 }\) x AD x EF
= \(\frac { 1 }{ 2 }\) x 24 x 15 cm² = 180 cm²
Area of shaded portion = 864 – 180 = 684 m²

Question 22.
Solution:
In the fig. ABCD is a rectangle in which AB = 40 cm, BC = 25 cm.
P, Q, R and S and the mid points of sides, PQ, QR, RS and SP respectively
Then PQRS is a rhombus.
Now, join PR and QS.
PR = BC = 25cm and QS = AB = 40cm
Area of PQRS = \(\frac { 1 }{ 2 }\) x PR x QS
= \(\frac { 1 }{ 2 }\) x 25 x 40 = 500 cm²

Question 23.
Solution:
(i) Length of rectangle (l) = 18 cm
and breadth (b) = 10 cm
Area = l x b = 18 x 10 = 180 cm²

Area of right ∆EBC = \(\frac { 1 }{ 2 }\) x 10 x 8 = 40 cm²
and area of right ∆EDF = \(\frac { 1 }{ 2 }\) x 10 x 6 = 30 cm²
Area of shaded region = 180 – (40 + 30) = 180 – 70 = 110 cm²
(ii) Side of square = 20 cm

Area of square = a² = (20)² = 400 cm²
Area of right ∆LPM = \(\frac { 1 }{ 2 }\) x 10 x 10 cm² = 50 cm²
Area of right ∆RMQ = \(\frac { 1 }{ 2 }\) x 10 x 20 = 100 cm²
and area of right ∆RSL = \(\frac { 1 }{ 2 }\) x 20 x 10 = 100 cm²
Area of shaded region = 400 – (50 + 100 + 100) cm2 = 400 – 250 = 150 cm²

Question 24.
Solution:
In the quadrilateral ABCD
BD = 24 cm
AL ⊥ BD and CM ⊥ BD
AL = 5 cm and CM = 8 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
In parallelogram ABCD,
Base AB = 32cm
Height DL = 16.5cm.

Area = Base x height = 32 x 16.5 cm² = 528 cm²

Question 2.
Solution:
Base of parallelogram = 1 m 60m = 160 cm
and height = 75 cm
Area = Base x height = 160 x 75 = 12000 cm²
= \(\frac { 12000 }{ 10000 }\) m² = 1.2m²

Question 3.
Solution:
Base of parallelogram = 14dm = 140cm
and height = 6.5 dm = 65cm
Area (in cm²) = Base x height = 140 x 65 = 9100 cm²
Area (in m²) = \(\frac { 140 }{ 100 }\) x \(\frac { 65 }{ 100 }\) = \(\frac { 9100 }{ 10000 }\)
= 0.91 m²

Question 4.
Solution:
Area of parallelogram = 54 cm²
Base = 15 cm

Question 5.
Solution:
Area of parallelogram ABCD = 153 cm²

Question 6.
Solution:
In parallelogram ABCD
AB || DC and AD || BC and AB = DC, AD = BC
AB = DC = 18cm, BC = 12cm
Area of parallelogram ABCD = Base x altitude = DC x AL = 18 x 6.4cm2 = 115.2 cm²
and area of parallelogram ABCD = BC x AM
⇒ 115.2 = 12 x AM
⇒ AM = 9.6 cm

Question 7.
Solution:
In parallelogram ABCD
AB = DC = 15 cm
BC = AD = 8 cm.

Distance between longer sides AB and DC is 4cm
i.e. perpendicular DL = 4cm.
DM ⊥ BC.
Area of parallelogram = Base x altitude = AB x DL = 15 x 4 = 60 cm²
Again let DM = x cm
area ABCD = BC x DM = 8 x x = 8x cm²
8x cm² = 60 cm²
⇒ x = 7.5 cm
Distance between shorter lines = 7.5 cm

Question 8.
Solution:
Let Base of the parallelogram = x

⇒ x² = 108 x 3 = 324 = (18)²
⇒ x = 18
Base = 18 cm
and altitude = \(\frac { 1 }{ 3 }\) x 18 = 6 cm

Question 9.
Solution:
Area of parallelogram = 512 cm²
Let height of the parallelogram = x
Then base = 2x
Area = Base x height
⇒ 512 = 2x x x
⇒ 2x² = 512
⇒ x² = 256 = (16)²
⇒ x = 16
Base = 2x = 2 x 16 = 32 cm
and height = x = 16 cm

Question 10.
Solution:
(i) Each side of rhombus = 12 cm
height = 7.5 cm

Area = Base x height = 12 x 7.5 = 90 cm²
(ii) Each side = 2 cm = 20 cm
Height = 12.6 cm
Area = Base x height = 20 x 12.6 = 252 cm²

Question 11.
Solution:
(i) Diagonals of rhombus ABCD are 16 cm and 28 cm

Question 12.
Solution:
In rhombus ABCD, diagonals AC and BD intersect each other at right angles at O.
AO = OC and BO = OD

AO = \(\frac { 1 }{ 2 }\) x AC = \(\frac { 1 }{ 2 }\) x 24 cm = 12cm
Let OB = x
Each side of rhombus = 20cm
In right ∆AOB
AO² + OB² = AB² (Pythagoras Theorem)
⇒ (12)² + OB² = (20)²
⇒ 144 + OB² = 400
⇒ OB² = 400 – 144 = 256 = (16)²
⇒ OB = 16
But BD = 2 BO = 2 x 16 = 32cm
Now, area of rhombus = \(\frac { Product of diagonals }{ 2 }\)
= \(\frac { 24 x 32 }{ 2 }\) cm2 = 384 cm²

Question 13.
Solution:
Area of rhombus = 148.8 cm²
one diagonal = 19.2 cm
Let second diagonal = x

Question 14.
Solution:
Area of rhombus = 119 cm²
Perimeter = 56 cm
Its side = \(\frac { 56 }{ 4 }\) = 14 cm

Question 15.
Solution:
Area of rhombus = 441 cm²
Height = 17.5 cm

Question 16.
Solution:
Base of a triangle = 24.8 cm
Corresponding height = 16.5 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
Outer length of plot (L) = 75 m
and breadth (B) = 60 m
Width of path inside = 2 m

Inner length (l) = 75 – 2 x 2 = 75 – 4 = 71 m
and width (b) = 60 – 2 x 2 = 60 – 4 = 56 m
Area of the path = L x B – l x b = (75 x 60 – 71 x 56) m² = 4500 – 3976 = 524 m²
Rate of constructing it = Rs. 125 per m²
Total cost = Rs. 524 x 125 = Rs. 65500

Question 2.
Solution:
Outer length of the plot (L) = 95 m
and breadth (B) = 72 m
Width of path = 3.5 m

Inner length (l) = 95 – 2 x 3.5 = 95 – 7 = 88 m
and breadth = 72 – 2 x 3.5 = 72 – 7 = 65 m
Outer area = L x B = 95 x 72 m² = 6840 m²
and inner area = l x b = 88 x 65 m² = 5720 m²
Area of path = outer area – inner area = 6840 – 5720 = 1120 m²
Rate of constructing it = Rs. 80 per m²
Total cost = Rs. 1120 x 80 = Rs. 89600
and rate of laying grass = Rs. 40 per m²
Total cost = Rs. 40 x 5720 = Rs. 228800
Total cost = Rs. 89600 + Rs. 228800 = Rs. 318400

Question 3.
Solution:
Length of saree (L) = 5 m
and breadth (B) = 1.3 m
Width of border = 25 cm
Inner length (l) = 5 – \(\frac { 2 x 25 }{ 100 }\) = 5 – 0.5 = 4.5 m
and inner breadth (b) = 1.3 – \(\frac { 2 x 25 }{ 100 }\) = 1.3 – 0.5 = 0.8 m
Now area of the boarder = L x B – l x b
= (5 x 1.3 – 4.5 x 0.8) m²
= 6.50 – 3.60
= 2.90 m²
= 2.90 x 100 x 100 = 29000 cm²
Cost of 10 cm² = Re. 1
Total cost = Rs. \(\frac { 29000 x 1 }{ 10 }\) = Rs. 2900

Question 4.
Solution:
Inner length of lawn (l) = 38 m
and breadth (b) = 25 m.
Width of path = 2.5 m.
Outer length (L) = 38 + 2 x 2.5 = 38 + 5 = 43 m
and outer breadth (B) = 25 + 2 x 2.5 = 25 + 5 = 30 m
Area of path = Outer area – Inner area
= (43 x 30 – 38 x 25) m²
=(1290 – 950) m² = 340 m²
Rate of gravelling the path = Rs. 120 per m²
Total cost = Rs. 120 x 340 = Rs. 40800

Question 5.
Solution:
Length’ of room (l) = 9.5m
Breadth (b) = 6m
Width of outer verandah = 1.25m
Outer length (L) = 9.5 + 2 x 1.25 = 9.5 + 2.5 = 12.0 m
and breadth (B) = 6 + 2 x 1.25 = 6 + 2.5 = 8.5 m
Area of verandah = Outer area – Inner area = L x B – l x b
= (12.0 x 8.5 – 9.5 x 6) m² – (102.0 – 57.0) m² = 45 m²
Rate of cementing = Rs. 15 per m²
Total cost = Rs. 80 x 45 = Rs. 3600

Question 6.
Solution:
Each side of square bed (a) = 2m 80 cm = 2.8 m
Width of strip = 30cm
Outer side (A) = 2.8 m + 2 x 30cm = 2.8 + 0.6 = 3.4m
Outer area = (3.4 m)² = 11.56 m²

Inner area = (2.8)² = 7.84 m²
Area of increased bed flower = 11.56 – 7.84 = 3.72 m²

Question 7.
Solution:
Ratio in length and breadth of the park = 2 : 1
Its perimeter = 240 m
Let length = 2x
then breadth = x
Perimeter = 2 (2x + x) = 2 x 3x = 6x
6x = 240
⇒ x = \(\frac { 240 }{ 6 }\) = 40
Length = 2x = 2 x 40 = 80m
and breadth = x = 40m
Area = L x B = 80 x 40 m² = 3200 m²
Width of path inside the park = 2m
Inner length (l) = 80 – 2 x 2 = 80 – 4 = 76 m
and breadth (b) = 40 – 2 x 2 = 40 – 4 = 36 m
Inner area = 76 x 36 = 2736 m²
Area of path = Outer area – Inner area = 3200 – 2736 = 464 m²
Rate of paving the path = Rs. 80 per m²
Total cost = Rs. 80 x 464 = Rs. 37120

Question 8.
Solution:
Length of hall (l) = 22m
Breadth (b) = 15.5 m
Space left along the walls = 75m = \(\frac { 3 }{ 4 }\) m
Inner length (l) = 22 – 2 x \(\frac { 3 }{ 4 }\) = 20.5 m
Inner breadth (b) = 15.5 – 2 x \(\frac { 3 }{ 4 }\) = 15.5 – 1.5 = 14m
Area of carpet = Inner area = 20.5 x 14 m² = 287 m²
Outer area = 22 x 15.5 = 341 m²
Area of strip left out = 341 – 287 = 54 m²
Width of carpet = 82 cm = \(\frac { 82 }{ 100 }\) m
Length of carpet = 287 ÷ \(\frac { 82 }{ 100 }\)
= \(\frac { 287 x 100 }{ 82 }\) = 350m
Rate of carpet = Rs. 60 per metre
Total cost = Rs. 60 x 350 = Rs. 21000

Question 9.
Solution:
Area of path = 165 m²
Width of path = 2.5m.
Let side of square lawn = x m.

Outer side = x + 2 x 2.5 = (x + 5) m
Area of path = (x + 5)² – x²
⇒ x² + 10x + 25 – x² = 165
⇒ 10x = 165 – 25 = 140
⇒ x = \(\frac { 140 }{ 10 }\) = 14m
Side of lawn = 14m
and area of lawn = (14)² m² = 196 m²

Question 10.
Solution:
Ratio in length and breadth of a park = 5 : 2
Width of path outside it = 2.5 m
Area of path = 305 m2
Let Inner length (l) = 5x
and breadth (b) = 2x
Outer length (L) = 5x + 2 x 2.5 = (5x + 5) m
Width (B) = 2x + 2 x 2.5 = (2x + 5) m
Area of path = Outer area – Inner area
⇒ (5x + 5) (2x + 5) – 5x x 2x = 305
⇒ 10x² + 10x + 25x + 25 – 10x² = 305
⇒ 35x = 305 – 25 = 280
⇒ x = 8
Length of park = 5x = 5 x 8 = 40m
and breadth = 2x = 2 x 8 = 16m
Dimensions of park = 40m by 16m

Question 11.
Solution:
Length of lawn (l) = 70 m
Breadth (b) = 50 m
Width of crossing roads = 5m

Area of roads = 70 x 5 + 50 x 5 – (5)²
= 350 + 250 – (5)²
= 600 – 25 = 575 m²
Cost of constructing = Rs. 120 per m²
Total cost Rs. 120 x 575 = Rs. 69000

Question 12.
Solution:
Length of lawn (l) = 115m
and breadth (b) = 64m.
Width of road parallel to length = 2m
and width of road parallel to breadth= 2.5m

Area of roads = (115 x 2 + 64 x 2.5 – 2 x 2.5) m²
= (230 + 160 – 5) m² = (390 – 5) m² = 385 m²
Cost of gravelling = Rs. 60 m²
Total cost = Rs. 60 x 385 = Rs. 23100

Question 13.
Solution:
Length of field (l) = 50 m
and breadth (b) = 40 m

Width of road parallel to length = 2 m
and width of road parallel to breadth = 2.5 m
Area of roads = 50 x 2 + 40 x 2.5 – 2.5 x 2 = (100 + 100 – 5) m² = 195 m²
and area of remaining portion = 50 x 40 – 195 = 2000 – 195 = 1805 m²

Question 14.
Solution:
(i) Outer length = 43m
and breadth = 27m
Area = 43 x 27 = 1161 m²
Inner length = 43 – 2 x 1.5 = 43 – 3 = 40m
and breadth = 27 – 2 x 1 = 27 – 2 = 25m
Inner area = 40 x 25 = 1000 m²
Area of shaded portion = 1161 – 1000 = 161 m²
(ii) Side of square (a) = 40m
Area = (a)² = 40 x 40 = 1600 m²
Area of larger road = 40 x 3 = 120 m²
and area of shorter road = 40 x 2 = 80 m²
Area of roads = (120 + 80) – 3 x 2 = 200 – 6 = 194 m²
Area of shaded portion = (1600 – 194) m² = 1406 m²

Question 15.
Solution:
(i) Outer length = 24m
and breadth = 19m
Area = 24 x 19 = 456 m²
Length of unshaded portion = 24 – 4 = 20m
and breadth = 16.5m
Area of unshaded portion = 20 x 16.5 m² = 330.0 m²
Area of shaded portion = 456 – 330 = 126 m²
(ii) Dividing the figure an shown
Area of rectangle I = 15 x 3 cm² = 45 cm²
Area of rectangle II = (12 – 3) x 3 = 9 x 3 = 27 cm²
Area of rectangle III = 5 x 3 = 15 cm²

and area of rectangle IV = (12 – 3) x 3 = 9 x 3 = 27 cm²
Total area of shaded portion = 45 + 27 + 15 + 27 = 114 cm²

Question 16.
Solution:
Dividing the figure an shown
Area of rectangle I = 3.5 x 0.5 m² = 1.75 m²
Area of rectangle II = (3.5 – 2 x 0.5) x 0.5 = (3.5 – 1) x 0.5 = 2.5 x 0.5 = 1.25 m²
Area of rectangle III = (2.5 – 1) x 0.5 = 1.5 x 0.5 = 0.75 m²
Area of rectangle IV = (1.5 – 1.0) x 0.5 x 0.5 = 0.25 m²

Total area of shaded portion = (1.75 + 1.25 + 0.75 + 0.25) m² = 4 m²

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
Length of rectangle (l) = 24.5 m
Breadth (b) = 18 m

Area = l x b = 24.5 x 18 m² = 441 m²
(ii) Length of rectangle (l) = 12.5 m
Breadth (b) = 8 cm = 0.80 m
Area = l x b = 12.5 x 0.80 m² = 10 m²

Question 2.
Solution:
Length of rectangular plot (l) = 48m
and its diagonal = 50m

Question 3.
Solution:
Ratio in the sides of a rectangle = 4 : 3
Area = 1728 cm²
Let length = 4x,
then breadth = 3x
Area = l x b
1728 = 4x x 3x
⇒ 12x² = 1728
⇒ x² = 144 = (12)²
⇒ x = 12
Length = 4x = 4 x 12 = 48 m
and breadth = 3m = 3 x 12 = 36m
Now perimeter = 2 (l + b) = 2 (48 + 36) m = 2 x 84 = 168 m
Rate of fencing = Rs. 30 per metre
Total cost= 168 x 30 = Rs. 5040

Question 4.
Solution:
Area of rectangular field = 3584 m²
Length = 64 m
Area = 3584
Breadth = \(\frac { Area }{ Length }\) = \(\frac { 3584 }{ 64 }\) = 56 m
Now perimeter = 2 (l + b) = 2 (64 + 56) m = 2 x 120 = 240 m
Distance covered in 5 rounds = 240 x 5 = 1200 m
Speed = 6 km/h
Time take = \(\frac { 1200 }{ 1000 }\) x \(\frac { 60 }{ 6 }\) = 12 minutes (1 hour = 60 minutes)

Question 5.
Solution:
Length of verandah (l) = 40m
Breadth (b) = 15m
Area = l x b = 40 x 15 = 600m²
Length of one stone = 6dm = \(\frac { 6 }{ 10 }\) m
and breadth = 5 dm = \(\frac { 5 }{ 10 }\) m
Area of one stone = \(\frac { 6 }{ 10 }\) x \(\frac { 5 }{ 10 }\)

Question 6.
Solution:
Length of a room = 13 m
Breadth = 9 m
Area of floor = l x b = 13 x 9 m² = 117 m²
or area of carpet = 117 m²
Width = 75 cm = \(\frac { 75 }{ 100 }\) = \(\frac { 3 }{ 4 }\) m
Length of carpet = Area ÷ Width
= 117 ÷ \(\frac { 3 }{ 4 }\)
= 117 x \(\frac { 4 }{ 3 }\) m
= 39 x 4 = 156 m
Rate = Rs. 105 per m
Total cost = Rs. 156 x 105 = Rs. 16380

Question 7.
Solution:
Cost of carpeting a room = Rs. 19200
Rate = Rs. 80 per m
Length of carpet = \(\frac { 19200 }{ 80 }\) m = 240 m
Width of carpet = 75 cm = \(\frac { 75 }{ 100 }\) = \(\frac { 3 }{ 4 }\) m
Area of carpet = 240 x \(\frac { 3 }{ 4 }\) = 180 m²
Length of a room = 15 m
Width = \(\frac { Area }{ Length }\) = \(\frac { 180 }{ 15 }\) = 12m

Question 8.
Solution:
Ratio in length and breadth of a rectangular piece of land = 5 : 3
Cost of fencing = Rs. 9600
and rate = Rs. 24 per m
Perimeter = \(\frac { 9600 }{ 24 }\) = 400 m
Let length = 5x
Then breadth = 3x
Perimeter = 2 (l + b)
⇒ 400 = 2 (5x + 3x)
⇒ 400 = 2 x 8x = 16x
⇒ 16x = 400
⇒ x = 25
Length of the land = 5x = 5 x 25 = 125 m
and width = 3x = 3 x 25 = 75 m

Question 9.
Solution:
Length of hall (l) = 10m.
Breadth (b) = 10m
and height (h) = 5m
Longest pole which can be placed in it

Question 10.
Solution:
Side of square (a) = 8.5m
Area = a² = (8.5)² = 8.5 x 8.5 m² = 72.25 m²

Question 11.
Solution:
(i) Length of diagonal of square = 72 cm.
Let length of side = a
Then diagonal = √2 a.
√2 a = 72

= 1.2 x √2 x 1.2 x √2 m²
= 1.44 x 2 = 2.88 m²

Question 12.
Solution:
Area of a square = 16200 m²
Side = √16200 m = √(8100 x 2) m = 90√2 m
Length of diagonal = √2 (side) = √2 x 90√2 = 180 m

Question 13.
Solution:
Area of square = \(\frac { 1 }{ 2 }\) hectare
= \(\frac { 1 }{ 2 }\) x 10000 m² = 5000 m²
side (a) = √Area = √5000 m = √(2500 x 2) = 50√2 m
Length of diagonal = √2 (side) = √2 x 50√2 = 100 m

Question 14.
Solution:
Area of sphere plot = 6084 m²
Side (a) = √Area = √6084 m = 78m
Perimeter = 4a = 4 x 78 = 312 m
Length of boundary four times = 312 x 4 = 1248 m

Question 15.
Solution:
Side of a square wire = 10 cm
Perimeter = 4a = 4 x 10 cm = 40 cm
or perimeter of rectangle = 40 cm
Length of rectangle = 12 cm
Breadth = \(\frac { 40 }{ 2 }\) – 12 = 20 – 12 = 8 cm
Now area of square = a² = (10)² = 100 cm²
and area of rectangle = l x b = 12 x 8 = 96 cm²
Difference in areas = 100 – 96 = 4 cm²
Square has 4 cm² more area

Question 16.
Solution:
Length of go down (l) = 50 m
Breadth (b) = 40 m
and height (h) = 10 m
Area of 4 walls = 2 (l + b) x h
= 2 (50 + 40) x 10 m
= 2 x 90 x 10 = 1800 m²
and area of ceiling = l x b = 50 x 40 = 2000 m²
Total area of walls and ceiling = 1800 + 2000 = 3800 m²
Rate of whitewashing = Rs. 20 per m²
Total cost = Rs. 20 x 3800 = Rs. 76000

Question 17.
Solution:
Area of 4 walls of a room= 168m²
Breadth of the room (b) = 10m
and height (h) = 4m.
Let l be the length of room
2 (l + b) h = 168
⇒ 2 (l + 10) x 4 = 168
⇒ l + 10 = \(\frac { 168 }{ 2 x 4 }\) = 21
⇒ l = 21 – 10 = 11m
Length of the room = 11 m

Question 18.
Solution:
Area of 4 walls of a room = 77 m²
Length of room (l) = 7.5 m
and breadth (b) = 3.5 m
Let h be the height,
then area of four walls = 2 (l + b) h
= 2 (7.5 + 3.5) h = 77
⇒ 2 x 11 x h = 77
⇒ h = \(\frac { 77 }{ 2 x 11 }\)
Height of room = 3.5 m

Question 19.
Solution:
Area of 4 walls = 120 m²
Height (h) = 4m.
Let breadth (b) = x
and length (l) = 2x
Area of 4 walls = 2 (l + h) x h = 2(2x + x) x 4 = 8 x 3x = 24x
24x = 120
x = \(\frac { 120 }{ 24 }\) = 5
Length of room = 2x = 2 x 5 = 10m
and breadth = x = 5m
Area of floor = l x b = 10 x 5 = 50 m²

Question 20.
Solution:
Length of a room (l) = 8.5 m
Breadth (b) = 6.5 m
and height (h) = 3.4 m
Area of four walls = 2 (l + b) x h
= 2 (8.5 +6.5) x 3.4 m²
= 2 x 15 x 3.4 m²
= 30 x 3.4= 102.0 m²
Area of two doors of size 1.5 m x 1 m = 2 x 1.5 x 1 m = 3 m²
and area of two windows of size 2 m x 1 m = 2 x 2 x 1 = 4 m²
Area of remaining portion = 102 – (3 + 4) = 102 – 7 m2 = 95 m²
Rate of painting = Rs. 160 per m²
Total cost = Rs. 160 x 95 = Rs. 15200

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.