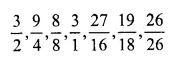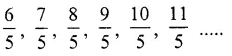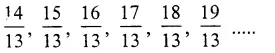CBSE Class 6

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

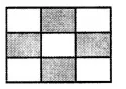
Question 1.
Solution:
(i) \(\\ \frac { 2 }{ 3 } \)
= \(\\ \frac { 2X2 }{ 3X2 } \)
= \(\\ \frac { 4 }{ 6 } \)

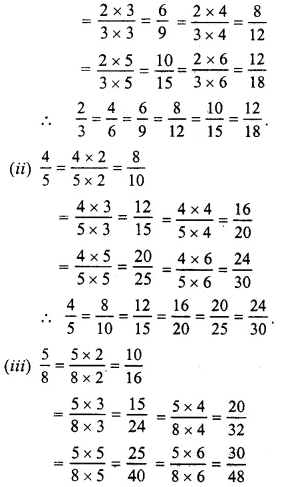
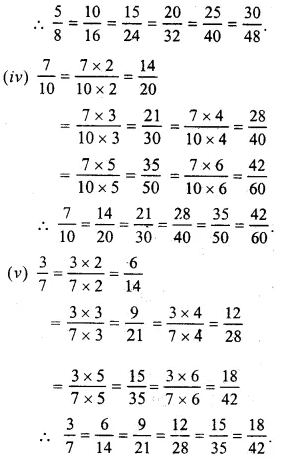
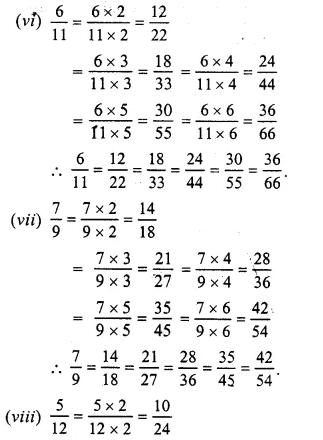
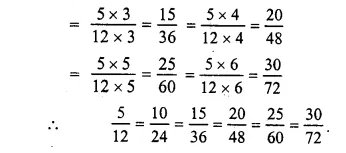
Question 2.
Solution:
(i) In \(\\ \frac { 5 }{ 6 } \) and \(\\ \frac { 20 }{ 24 } \)
\(\\ \frac { 5 }{ 6 } \) = \(\\ \frac { 20 }{ 24 } \)

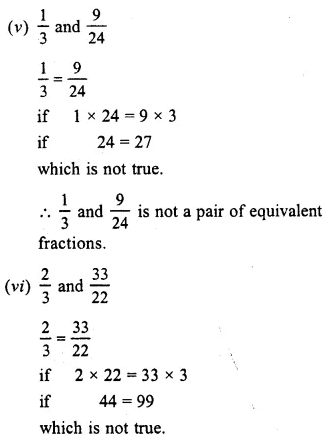
Question 3.
Solution:
Equivalent fraction of \(\\ \frac { 3 }{ 5 } \) having
(i) Denominator = 30 and 30 = 5 x 6

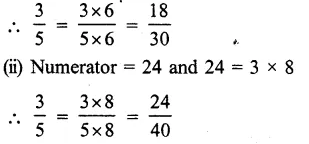
Question 4.
Solution:
(i) Denominator = 54, and 54 = 9 x 6

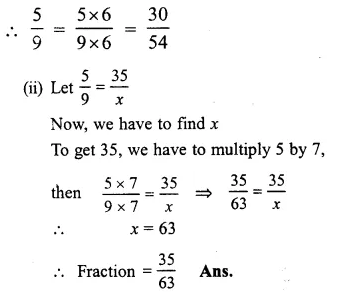
Question 5.
Solution:
Equivalent fraction of \(\\ \frac { 6 }{ 11 } \) having
(i) Denominator = 77 and 77 = 11 = 7
\(\\ \frac { 6 }{ 11 } \)
= \(\\ \frac { 6X7 }{ 11X7 } \)
= \(\\ \frac { 42 }{ 77 } \)
(ii) Numerator = 60 and 60 = 6 x 10
\(\\ \frac { 6 }{ 11 } \)
= \(\\ \frac { 6X10 }{ 11X10 } \)
= \(\\ \frac { 60 }{ 110 } \)

Question 6.
Solution:
Let \(\\ \frac { 24 }{ 30 } \) = \(\\ \frac { 4 }{ x } \)
In order to get 4, divide 24 by 6,

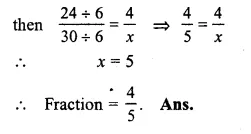
Question 7.
Solution:
Equivalent fraction of \(\\ \frac { 36 }{ 48 } \), with
(i) Numerator 9 and 9 = 36 + 4
\(\frac { 36 }{ 48 } =\frac { 36\div 4 }{ 48\div 4 } =\frac { 9 }{ 12 } \)
(ii) Denominator = 4 and 4 = 48 ÷ 12
\(\frac { 36 }{ 48 } =\frac { 36\div 12 }{ 48\div 12 } =\frac { 3 }{ 4 } \)

Question 8.
Solution:
Equivalent fraction of \(\\ \frac { 56 }{ 70 } \) with
(i) Numerator 4 and = 56 ÷ 14
\(\frac { 56 }{ 70 } =\frac { 56\div 14 }{ 70\div 14 } =\frac { 4 }{ 5 } \)
(ii) Denominator =10 and 10 = 70 ÷ 7
\(\frac { 56 }{ 70 } =\frac { 56\div 7 }{ 70\div 7 } =\frac { 8 }{ 10 } \)

Question 9.
Solution:
(i) In \(\\ \frac { 9 }{ 15 } \), HCF of 9 and 15 = 3
Now, dividing each term by 3, we get:
\(\frac { 9 }{ 15 } =\frac { 9\div 3 }{ 15\div 3 } =\frac { 3 }{ 5 } \)

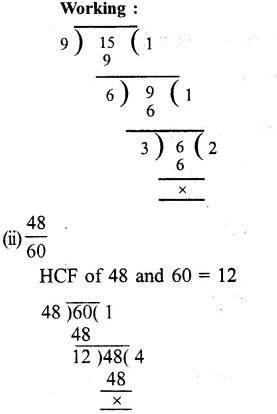
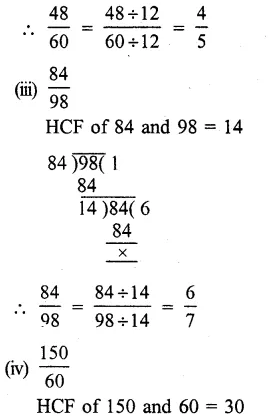
Question 10.
Solution:
We know that a fraction is in its simplest form if its HCF of numerator and denominator is 1.

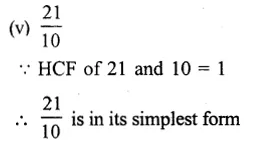
Question 11.
Solution:

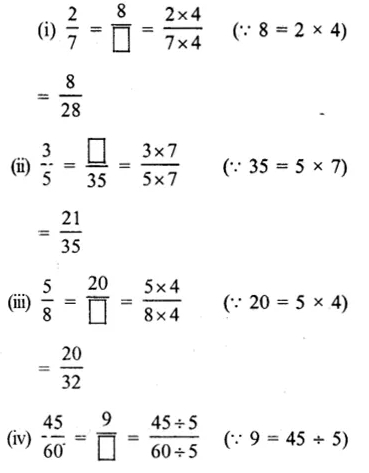
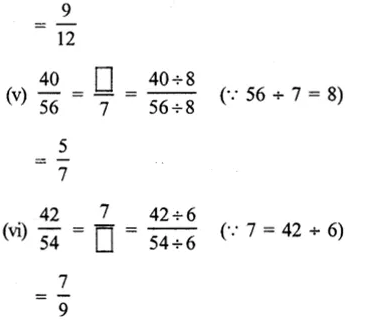
Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Question 1.
Solution:
We know that, a fraction is proper if its denominator is greater than its numerator. Therefore,
\(\\ \frac { 1 }{ 2 } \), \(\\ \frac { 3 }{ 5 } \) and \(\\ \frac { 10 }{ 11 } \) are proper fractions. Ans.

Question 2.
Solution:
We know that a fraction is improper if its denominator is less than its numerator
Therefore,

are improper fractions. Ans.

Question 3.
Solution:
Six improper fractions with denominator 5 can be

Question 4.
Solution:
Six improper fraction with denominator 13 can be

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 5 Fractions Ex 5A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5B
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5C
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5D
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5E
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5F
• RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5G

Question 1.
Solution:
(i) \(\\ \frac { 3 }{ 4 } \)
(ii) \(\\ \frac { 1 }{ 4 } \)
(iii) \(\\ \frac { 2 }{ 3 } \)
(iv) \(\\ \frac { 3 }{ 10 } \)
(v) \(\\ \frac { 4 }{ 9 } \)
(vi) \(\\ \frac { 3 }{ 8 } \)

Question 2.
Solution:
In the figure, \(\\ \frac { 4 }{ 9 } \) is shaded

Question 3.
Solution:
In the figure, whole rectangle is not divided into four equal parts.

Question 4.
Solution:
(i) Three-fourths = \(\\ \frac { 3 }{ 4 } \)
(ii) Four-sevenths = \(\\ \frac { 4 }{ 7 } \)
(iii) Two-fifths = \(\\ \frac { 2 }{ 5 } \)
(iv) Three-tenths = \(\\ \frac { 3 }{ 10 } \)
(v) One-eighth = \(\\ \frac { 1 }{ 8 } \)
(vi) three-tenths = \(\\ \frac { 5 }{ 6 } \)
(vii) five-sixths = \(\\ \frac { 8 }{ 9 } \)
(vii) seven-twelfths = \(\\ \frac { 7 }{ 12 } \)

Question 5.
Solution:
(i) In \(\\ \frac { 4 }{ 9 } \), numerator is 4 and denominator is 9.
(ii) In \(\\ \frac { 6 }{ 11 } \), numerator is 6 and denominator is 11.
(iii) In \(\\ \frac { 8 }{ 15 } \), numerator is 8 and denominator is 15.
(iv) In \(\\ \frac { 12 }{ 17 } \), numerator is 12 and denominator is 17.
(v) \(\\ \frac { 5 }{ 1 } \) , numerator is 5 and denominator is 1.

Question 6.
Solution:
(z) Numerator = 3, Denominator = 8, then fraction = \(\\ \frac { 3 }{ 8 } \).
(ii) Numerator = 5, Denominator = 12, then fraction = \(\\ \frac { 5 }{ 12 } \)
(iii) Numerator = 7, Denominator = 16, then fraction = \(\\ \frac { 7 }{ 16 } \).
(iv) Numerator = 8, Denominator = 15, then fraction = \(\\ \frac { 8 }{ 15 } \)

Question 7.
Solution:
(i) \(\\ \frac { 2 }{ 3 } \) = two-thirds
(ii) \(\\ \frac { 4 }{ 9 } \) = four-ninths
(iii) \(\\ \frac { 2 }{ 5 } \) = two-fifths
(iv) \(\\ \frac { 7 }{ 10 } \) = seven-tenths
(v) \(\\ \frac { 1 }{ 3 } \) = one-thirds
(vi) \(\\ \frac { 3 }{ 4 } \) = three-fourth
(vii) \(\\ \frac { 3 }{ 8 } \) = three-eighths
(viii) \(\\ \frac { 9 }{ 14 } \) = nine-fourteenths
(ix) \(\\ \frac { 5 }{ 11 } \) = five-elevanths
(x) \(\\ \frac { 6 }{ 15 } \) = six-fifteenths

Question 8.
Solution:
24 minutes is the fraction of 1 hour i.e.,
60 minutes = \(\\ \frac { 24 }{ 60 } \)

Question 9.
Solution:
Natural number between 2 to 10 are 2, 3, 4, 5, 6, 7, 8, 9, 10 = 9
Out of these prime number are 2, 3, 5, 7 = 4
Fraction = \(\\ \frac { 4 }{ 9 } \)

Question 10.
Solution:
(i) \(\\ \frac { 2 }{ 3 } \) of 15 pens = \(\\ \frac { 2 }{ 3 } \) x 15 = 2 x 5 = 10 pens.
(ii) \(\\ \frac { 2 }{ 3 } \) of 27 balls = \(\\ \frac { 2 }{ 3 } \) x 27 = 2 x 9 = 18 balls.
(iii) \(\\ \frac { 2 }{ 3 } \) of 36 balloons = \(\\ \frac { 2 }{ 3 } \) x 36 = 2 x 12 = 24 balloons. Ans.

Question 11.
Solution:
(i) \(\\ \frac { 3 }{ 4 } \) of 16 cups = \(\\ \frac { 3 }{ 4 } \) x 16 = 3 x 4
= 12 cups.
(ii) \(\\ \frac { 3 }{ 4 } \) of 28 rackets = \(\\ \frac { 3 }{ 4 } \) x 28 = 3 x 7
= 21 rackets.
(iii) \(\\ \frac { 3 }{ 4 } \) of 32 books = \(\\ \frac { 3 }{ 4 } \) x 32 = 3 x 8
= 24 books. Ans.

Question 12.
Solution:
Total number of pencils Neelam has = 25
No. of pencils given to Meena
= \(\\ \frac { 4 }{ 5 } \) of 25
= \(\\ \frac { 4 }{ 5 } \) x 25 – 20
No. of pencils left with Neelam = 25 – 20 = 5

Question 13.
Solution:
(i) \(\\ \frac { 3 }{ 8 } \)
Take a line segment OA = one unit of length
Divide it into 8 equal parts and take 3 parts at P, then P represents \(\\ \frac { 3 }{ 8 } \).

(ii) \(\\ \frac { 5 }{ 9 } \)
(a) Take a line segment OA = one unit of length.
(b) Divide it into nine equal parts and take 5 parts at P, then P represents \(\\ \frac { 5 }{ 9 } \).

(iii) \(\\ \frac { 4 }{ 7 } \)
(a) Take a line segment OA = one unit of length.
(b) Divide it into 7 equal parts and take 4 parts at P then P represents \(\\ \frac { 4 }{ 7 } \).

(iv) \(\\ \frac { 2 }{ 5 } \)
(a) Take a line segment OA = 1 unit of length.
(b) Divide it with 5 equal parts and take 2 parts and P then P represents \(\\ \frac { 2 }{ 5 } \).

(v) \(\\ \frac { 1 }{ 4 } \)
(a) Take a line segment OA = 1 unit of length.
(b) Divide it with 4 equal parts and take 1 parts and P then P represents \(\\ \frac { 1 }{ 4 } \).

Hope given RS Aggarwal Solutions Class 6 Chapter 5 Fractions Ex 5A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4F

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4A
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F

OBJECTIVE QUESTIONS
Tick the correct answer in each of the following :

Question 1.
Solution:
(b) Because – 4 < – 3.

Question 2.
Solution:
Because – 3 – 2 = – 5.

Question 3.
Solution:
(c) Because 4 + ( – 5) = – 1.

Question 4.
Solution:
(a) Because – 7 – 2 = – 9.

Question 5.
Solution:
(b) Because 7 + | – 3| = 7 + 3 = 10.

Question 6.
Solution:
(c) Because – 42 + ( – 35) = – 42 – 35 = – 77.

Question 7.
Solution:
(b) Because ( – 37) + 6 = – 31.

Question 8.
Solution:
(c) Because 49 + ( – 27) = 49 – 27 = 22.

Question 9.
Solution:
(c) Because successor of – 18 = – 18 + 1 = – 17.

Question 10.
Solution:
(b) Because predecessor of – 16 is = – 16 – 1 = – 17.

Question 11.
Solution:
(a) Because additive inverse of – 5 is = – ( – 5) = 5.

Question 12.
Solution:
(b) Because – 12 – ( – 5) = – 12 + 5 = – 7

Question 13.
Solution:
(b) Because 5 – ( – 8) = 5 + 8 = 13.

Question 14.
Solution:
(c) Because other – 25 – 30 = – 55.

Question 15.
Solution:
(a) Because other 20 – ( – 5) = 20 + 5 = 25.

Question 16.
Solution:
(b) Because other – 13 – 8 = – 21.

Question 17.
Solution:
(b) Because 0 – ( – 8) = 0 + 8 = 8

Question 18.
Solution:
(c) Because 8 + ( – 8) = 8 – 8 = 0.

Question 19.
Solution:
(c)Because- 6 + 4 – ( – 3) = – 6 + 4 + 3 = 7 – 6 = 1.

Question 20.
Solution:
(c) Because 6 – ( – 4) = 6 + 4 = 10.

Question 21.
Solution:
(a) Because ( – 7) + ( – 9) + 12 + ( – 16) = – 7 – 9 + 12 – 16 = – 32 + 12 = – 20.

Question 22.
Solution:
(c) Because – 4 – (8) = – 4 – 8 = – 12.

Question 23.
Solution:
(c) Because – 6 – ( – 9) = – 6 + 9 = 3.

Question 24.
Solution:
(c) Because 10 – ( – 5) = 10 + 5 = 15.

Question 25.
Solution:
(b) Because ( – 6) x 9 = 54.

Question 26.
Solution:
(a) Because ( – 9) x 6 + ( – 9) x 4
= – 54 – 36 = – 90.

Question 27.
Solution:
(b) Because 36 + ( – 9) = \(\\ \frac { 36 }{ -9 } \) = – 4.

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4A
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E
• RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F

Question 1.
Solution:
(i) 85 ÷ ( – 17) = \(\\ \frac { 85 }{ -17 } \) = – 5
(ii) ( – 72) ÷ 18 = \(\\ \frac { -72 }{ 18 } \) = – 4
(iii) ( – 80) ÷ 16 = \(\\ \frac { -80 }{ 16 } \) = – 5
(iv) ( – 121) ÷ 11 = \(\\ \frac { -121 }{ 11 } \) = – 11
(v) 108 ÷ ( – 12) = \(\\ \frac { 108 }{ -12 } \) = – 9
(vi) ( – 161) ÷ 23 = \(\\ \frac { -161 }{ 23 } \) = – 7
(vii) ( – 76) ÷ ( – 19) = \(\\ \frac { -76 }{ -19 } \) = 4
(viii) ( – 147) + ( – 21) = \(\\ \frac { -147 }{ -21 } \) = 7
(ix) ( – 639) ÷ ( – 71) = \(\\ \frac { -639 }{ -71 } \) = 9
(x) ( – 15625) ÷ ( – 125) = \(\\ \frac { -15625 }{ -125 } \)

(xi) 2067 ÷ ( – 1) = \(\\ \frac { 2067 }{ -1 } \) = – 2067
(xii) 1765 ÷ ( – 1765) = \(\\ \frac { 1765 }{ -1765 } \) = – 1
(xiii) 0 ÷ ( – 278) = \(\\ \frac { 0 }{ -278 } \) = 0
(xiv) 3000 ÷ ( – 100) = \(\\ \frac { 3000 }{ -100 } \) = – 30

Question 2.
Solution:
(i) 80 ÷ (…..) = – 5
Let 80 ÷ a = – 5
then, a = 80 ÷ ( – 5) = – 16
80 ÷ ( – 16) = – 5
(ii) – 84 + (…..) = – 7
Let – 84 ÷ a = – 7
then a = \(\\ \frac { -84 }{ -7 } \) = 12s
– 84 ÷ 12 = – 7
(iii)(….) ÷ ( – 5) = 25
Let a + ( – 5) = 25
a = 25 x ( – 5) = – 125
( – 125) ÷ ( – 5) = 25
(iv)(……) ÷ 372 = 0
Let a ÷ 372 = 0
Then a = 6 x 372 = 0
(0) ÷ 372 = 0
(v)(….) ÷ 1 = – 186
Let a ÷ 1 = – 186
Then a = – 186 x 1 = – 186
( – 186) ÷ 1 = – 186
(vi)(…..) ÷ 17 = – 2
Let a ÷ 17 = – 2
Then a = – 2 x 17 = – 34
( – 34) ÷ 17 = – 2
(vii) (….) ÷ 165 = – 1
Let a ÷ 165 = – 1
Then a = – 1 x 165 = – 165
( – 165) ÷ 165 = – 1
(viii) (….) + ( – 1) = 73
Let a ÷ ( – 1) = 73
Then a = 73 ( – 1) = – 73
( – 73) + ( – 1) = 73
(ix) 1 ÷ (…..) = – 1
Let 1 ÷ (a) = – 1
Then a = – 1 x 1 = – 1
1 ÷ ( – 1) = – 1 Ans.

Question 3.
Solution:
(i) True : as if zero is divided by any non-zero integer, then quotient is always zero.
(ii) False : As division by zero is not admissible.
(iii) True : As dividing by one integer by another having opposite signs is negative.
(iv) False : As dividing one integer by another having the same signs is positive not negative.
(v) True : As dividing one integer by another with same sign is always positive.
(vi) True : As dividing one integer by another having opposite signs is always negative.
(vii) True : As dividing one integer by another having opposite signs is always negative.
(viii) True : As dividing one integer by another having opposite signs is always negative.
(ix) False : As dividing one integer by another having same signs is always positive not negative

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.