RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B
These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B.
Other Exercises
- RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4A
- RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B
- RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C
- RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D
- RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4E
- RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4F
Question 1.
Solution:
(i) On the number line we start from 0 and move 9 steps to the right to reach a point A. Now, starting from A, we move 6 steps to the left to reach a point B, as shown below :
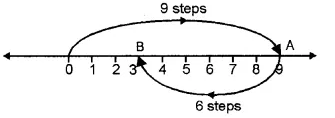
Now, B represents the integer 3
9 + ( – 6) = 3
(ii) On the number line, we start from 0 and move 3 steps to the left to reach a point A. Now, starting from A, we move 7 steps to the right to reach a point B, as shown below :
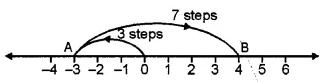
And B represents the integer 4
( – 3) + 7 = 4
(iii) On the number line, we start from 0 and move 8 steps to the right to reach a point A. Now, starting from A, we move 8 steps to the left to reach a point B, as shown below :
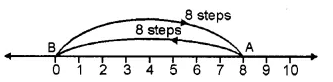
And, B represents the integer 0.
8 + ( – 8) = 0
(iv) On the number line, we start from 0 and move 1 step the left to reach a point A. Now, starting from point A, we move 3 steps to the left to reach g. point B, as shown below :
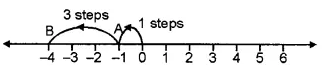
And, B represents the integer – 4
( – 1) + ( – 3) = – 4.
(v) On the number line, we start from 0 and move 4 steps to the left to reach a point A. Now, starting from point A, we move 7 steps to the left to reach a point B, as shown below :
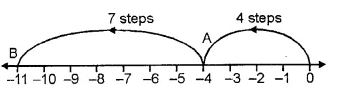
And, B represents the integer -11.
( – 4) + ( – 7) = – 11
(vi) On the number line we start from 0 and move 2 steps to the left to reach a point A. Now, starting from A, we move 8 steps to the left to reach a point B, as shown below :
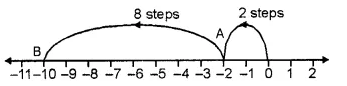
And, B represents the integer – 10
( – 2) + ( – 8) = – 10
(vii) On the number line we start from 0 and move 3 steps to the right to reach a point A. Now, starting from A, we move 2 steps to the left to reach a point B and again starting from left to reach a point B and again starting from B, we move 4 steps to the left to reach a point C, as shown below :
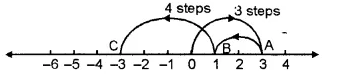
And, C represents the integer – 3
3 + ( – 2) + ( – 4) = – 3
(viii) On the number line we start from 0 and move 1 step to the left to reach a point A. Now, starting from A, we move 2 steps to the left to reach a point B and again starting from B, we move 3 steps to the left to reach point C, as shown below :
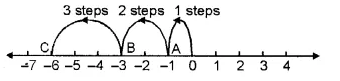
And, C represents the integer – 6
( – 1) + ( – 2) + ( – 3) = – 6.
(ix) On the number line we start from 0 and move 5 steps to the right to reach a point A. Now, starting from A, we move 2 steps to the left to reach a point B and again starting from point B, we move 6 steps to the left to reach a point C, as shown below :
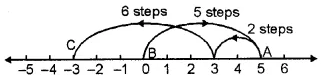
And, C represents the integer – 3.
5 + (- 2) + (- 6) = – 3
Question 2.
Solution:
(i) (- 3) + ( – 9) = – 12
(Using the rule for addition of integers having like signs)
(ii) ( – 7) + ( – 8) = – 15
(Using the rule for addition of integers having like signs)
(iii) ( – 9) + 16 = 7
(Using the rule for addition of integers having unlike signs)
(iv) ( – 13) + 25 = 12
(Using the rule for addition of integers having unlike signs)
(v) 8 + ( – 17) = – 9
(Using the rule for addition of integers having unlike signs)
(vi) 2 + ( – 12) = – 10
(Using the rule for addition of integers having unlike signs)
Question 3.
Solution:
(i) Using the rule for addition of integers with like signs, we get:
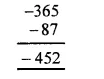
(ii) Using the rule for addition of integers with like signs, we get :
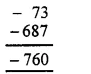
(iii) Using the rule for addition of integers with like signs, we get :
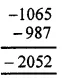
(iv) Using the rule for addition of integers with like signs, we get:
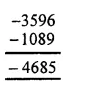
Question 4.
Solution:
(i) Using the rule for addition of integers with unlike signs, we get:
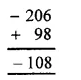
(ii) Using the rule for addition of integers with unlike signs, we get:
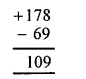
(iii) Using the rule for addition of integers with unlike signs, we have
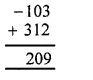
(iv) Using the rule for addition of integers with unlike signs, we have
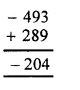
Question 5.
Solution:
(i) Using the rule for addition of integers with unlike signs, we get :
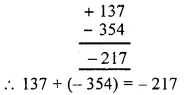
(ii) Using-the rule for addition of integers with unlike signs, we get
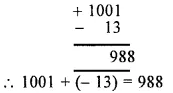
(iii) Using the rule for addition of integers with unlike signs, we get :
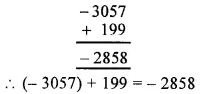
(iv) Using the rule for addition of integers with unlike signs, we get :
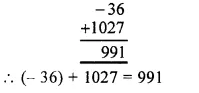
(v) Using the rule for addition of integers with like signs, we get:
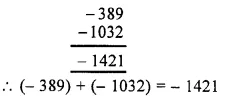
(vi) Using the rule for addition of integers with unlike signs, we get :
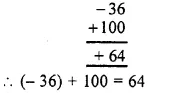
(vii) Using the rule for addition of integers with unlike signs, we get :
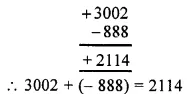
(viii) We have, ( – 18) + 25 + ( – 37)
= [( – 18) + 25] + ( – 37)
= 7 + ( – 37)
= – 30
(ix) We have, – 312 + 39 + 192
= ( – 312) + (39 + 192)
= ( – 312) + 231
= – 81
(x) We have ( – 51) + ( – 203) + 36 + ( – 28)
= [( – 51) + ( – 203)] + [36 + ( – 28)]
= ( – 254) + 8
= – 246
Question 6.
Solution:
(i) The additive inverse of – 57 is 57
(ii) The additive inverse of 183 is – 183
(iii) The additive inverse of 0 is 0
(iv) The additive inverse of – 1001 is 1001
(v) The additive inverse of 2054 is – 2054
Question 7.
Solution:
(i) Successor of 201 = 201 + 1 = 202
(ii) Successor of 70 = 70 + 1 = 71
(iii) Successor of – 5 = – 5 + 1 = – 4
(iv) Successor of – 99 = – 99 + 1 = – 98
(v) Successor of – 500 = – 500 + 1 = – 499 Ans.
Question 8.
Solution:
(i) Predecessor of 120 = 120 – 1 = 119
(ii) Predecessor of 79 = 79 – 1 = 78
(iii) Predecessor of – 8 = – 8 – 1 = – 9
(iv) Predecessor of – 141 = – 141 – 1 = – 142
(v) Predecessor of – 300 = – 300 – 1 = – 301 Ans.
Question 9.
Solution:
(i) ( – 7) + ( – 9) + 12 + ( – 16)
= – 7 – 9 + 12 – 16
= – 7 – 9 – 16 + 12
= – 32 + 12
= – 20
(ii) 37 + ( – 23) + ( – 65) + 9 + ( – 12)
= 37 – 23 – 65 + 9 – 12
= 37 + 9 – 23 – 65 – 12
= 46 – 100
= – 54
(iii) ( – 145) + 79 + ( – 265) + ( – 41) + 2
= – 145 + 79 – 265 – 41 + 2
= 79 + 2 – 145 – 265 – 41
= 81 – 451
= – 370
(iv) 1056 + ( – 798) + ( – 38) + 44 + ( – 1)
= 1056 – 798 – 38 + 44 – 1
= 1056 + 44 – 798 – 38 – 1
= 1100 – 837
= 263 Ans.
Question 10.
Solution:
Distance travelled from Patna to its north = 60 km
Distance travelled from that place to south of it = 90 km
Distance of the final place to Patna = 60 – 90
= – 30 km
= 30 km south
Ans.
Question 11.
Solution:
Total amount of pencils purchased = Rs. 30 + Rs. 25
= Rs 55
Total amount of pens purchased = Rs. 90
Total cost price = Rs. 55 + Rs. 90
= Rs. 145
Total sale price of pencils and pens = Rs 20 + Rs. 70
= Rs. 90
Loss = cost price – selling price
= Rs. 145 – Rs. 90
= Rs. 55 Ans.
Question 12.
Solution:
(i) True.
(ii) False : As if positive integer is greater then it will be positive.
(iii) True : As ( – a + a = 0).
(iv) False : As the sum of three integers can be zero or non-zero.
(v) False : As | – 5 | = 5 and | – 3 | = 3 and 5 ≮ 3.
(vi) False : | 8 – 5 | = | 3 | = 3 and | 8 | + | – 5 | = 8 + 5 = 13.
Question 13.
Solution:
(i) a + 6 = 0
Subtracting 6 from both sides,
a + 6 – 6 = 0 – 6
=> a = – 6
a = – 6.
(ii) 5 + a = 0
Subtracting 5 from both sides,
5 + a – 5 = 0 – 5
=> a = – 5
a = – 5
(iii) a + ( – 4) = 0
Adding 4 to both sides,
a + ( – 4) + 4 = 0 + 4
=> a = 4
a = 4
(iv) – 8 + a = 0
Adding 8 to both sides,
– 8 + a + 8 = 0 + 8
=> a – 8
a = 8 Ans.
Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.