CBSE Class 12

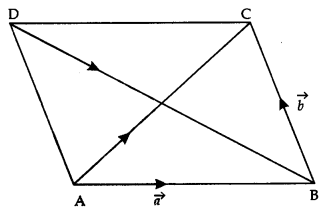
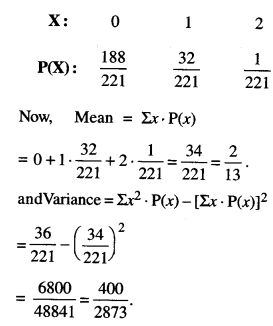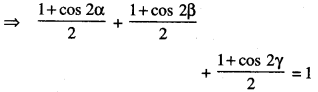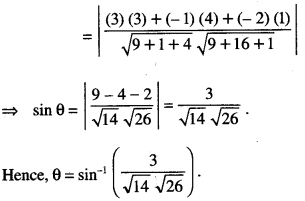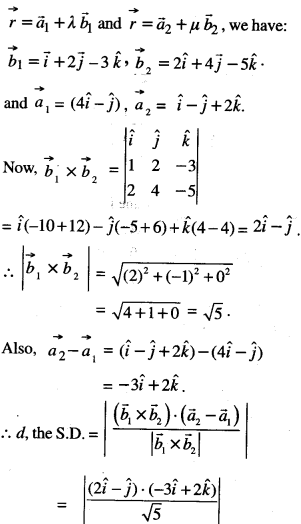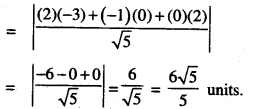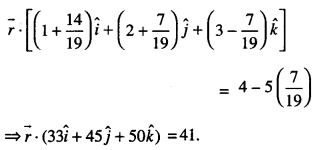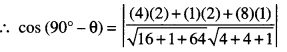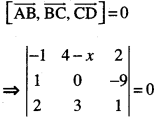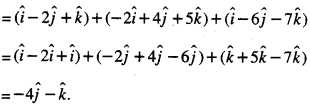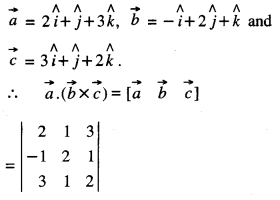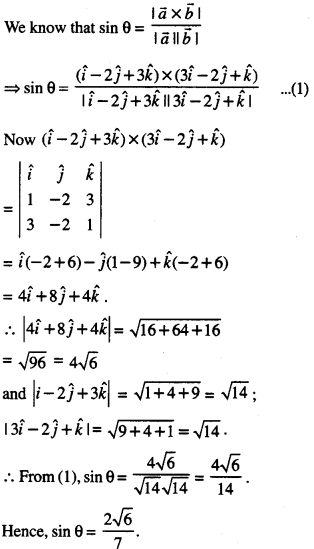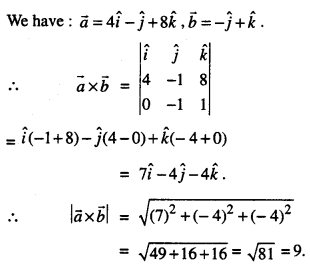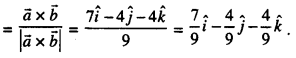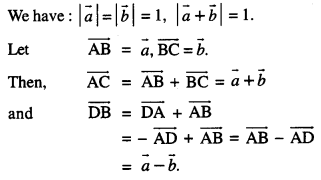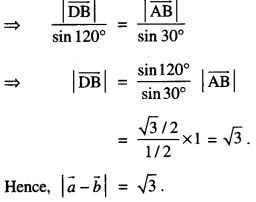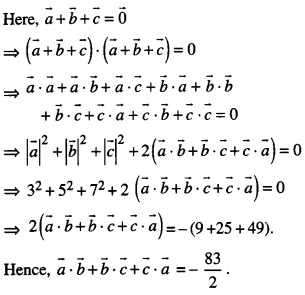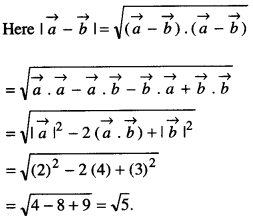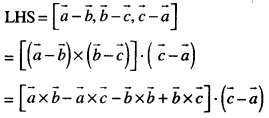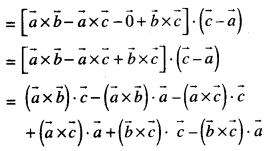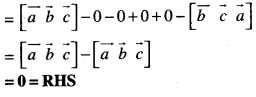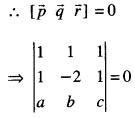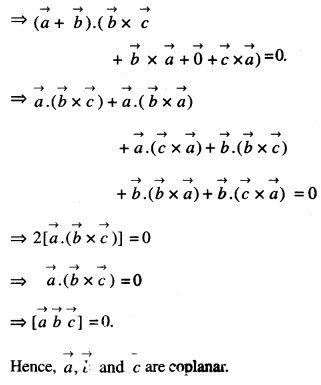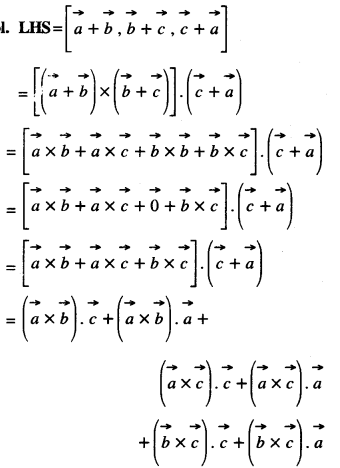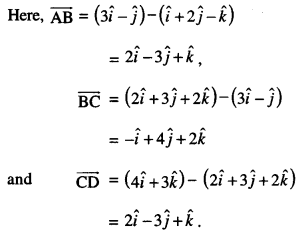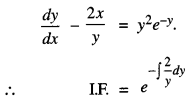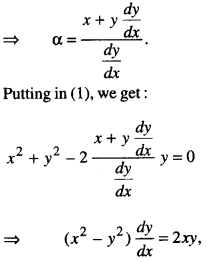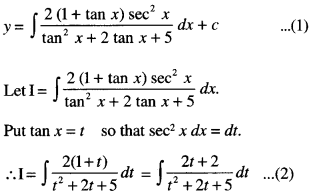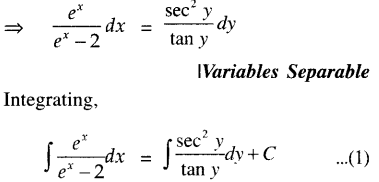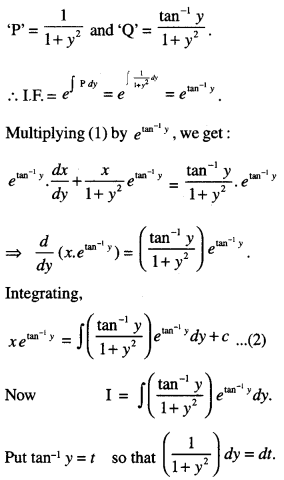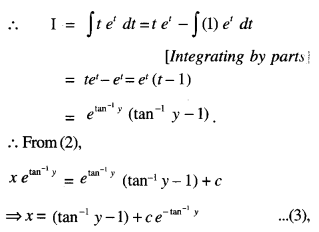Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 13 Probability. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 13 Important Extra Questions Probability

Probability Important Extra Questions Very Short Answer Type

Question 1.
If A and B are two independent event, prove that A’ and B are also independent.
(C.B.S.E. Sample Paper 2018-19)
Solution:
Since A and B are independent events, [Given]
.-. P (A ∩ B) = P (A) . P(B) …(1)
Now P(A’∩B) = P (B) – P (A ∩ B)
= P(B) – P (A) P( ∩ B) [Using (1)]
= (1 – P(A)) P(B) = P(A’) P(B).
Hence, A’ and B are independent events.

Question 1.
One card is drawn from a pack of 52 cards so that each card is equally likely to be se-lected. Prove that the following cases are in-dependent :
(a) A : “The card drawn is a spade”
B : “The card drawn is an ace.”
(N.C.E.R.T.)
(b) A : “The card drawn is black”
B : “The card drawn is a king.”
(.N.C.E.R.T.)
Solution:
(a) P(A) =\(\frac{13}{52}=\frac{1}{4}\),P(B) = \(\frac{4}{52}=\frac{1}{13}\)
P(A∩B) = \(\frac{1}{52}=\frac{1}{4} \cdot \frac{1}{13}\) = p(A).p(B)
Hence, the events A and B are independent

(b) P(A) = \(\frac{26}{52}=\frac{1}{2}\), P(B) = \(\frac{4}{52}=\frac{1}{13}\)
P(A∩B) = \(\frac{2}{52}=\frac{1}{26}=\frac{1}{2} \cdot \frac{1}{13}\) = P(A).P(B)
Hence, the events A and B are independent

Question 3.
A pair of coins is tossed once. Find the probability of showing at least one head.
Solution:
S, Sample space = {HH, HT, TH, TT}
where H ≡ Head and T ≡ Tail.
∴ P (at least one head) = \(\frac { 3 }{ 4 }\) .

Question 4.
P(A) = 0.6, P(B) = 0. 5 and P(A/B) = 0.3, then find P(A∪ B)
(C.B.S.E. Sample Paper 2018-19)
Solution:
We have: P(A/B) = 0.3
\(\frac{P(A \cap B)}{P(B)}\) = 0.3
\(\frac{P(A \cap B)}{0.5}\) = 0.3
P (A ∩ B) = 0.5 x 0.3 = 0.15.
Now, P(A∪B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.5 – 0. 15
Hence, P (A ∪ B) = 1.1 – 0.15 = 0.95.

Question 5.
One bag contains 3 red and 5 black balls. Another bag contains 6 red and 4 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is red. (C.B.S.E. Sample Paper 2018-19)
Solution:
P(Red transferred and red drawn or black trans¬ferred red drawn)
\(\begin{array}{l}
=\frac{3}{8} \times \frac{7}{11}+\frac{5}{8} \times \frac{6}{11} \\
=\frac{21}{88}+\frac{30}{88}=\frac{51}{88}
\end{array}\)

Question 6.
Evaluate P(A ∪ B), if 2P(A) = P(B) = \(\frac { 5 }{ 13 }\) and P(A/B) = \(\frac { 2 }{ 5 }\) (C.B.S.E. 2018 C)
Solution:
P(A/B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\) P(A∩B) = \(\frac{2}{11}\)
P(A∪B) = P(A) + P(B) – (A ∩ B)
= \(\frac{5}{26}+\frac{5}{13}-\frac{2}{13}=\frac{11}{26}\)

Probability Important Extra Questions Short Answer Type

Question 1.
Given that A and B are two independent events such that P(A) = 0.3 and P(B) = 0.5. Find P(A/B). (C.B.S.E. 2019 C)
Solution:
We have:
P(A)= 0.3 and P(B) = 0.5.
Now P(A ∩ B) = P(A). P(B)
[∵A and B are independent events]
= (0.3) (0.5) = 0.15.
Hence, P(A/B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}=\frac{0.15}{0.5}\) =0.3.

Question 2.
A bag contains 3 white and 2 red balls, another bag contains 4 white and 3 red balls. One ball is drawn at random from each bag.
Find the probability that the balls drawn are one white and one red.
(C.B.S.E. 2019 C)
Solution:
Reqd. probability
= P(White, Red) + P (Red, White)
\(\frac{3}{5} \times \frac{3}{7}+\frac{2}{5} \times \frac{4}{7}=\frac{9}{35}+\frac{8}{35}=\frac{17}{35}\)

Question 3.
The probabilities of A, B and C solving a problem independently are \(\frac{1}{2}, \frac{1}{3}\) and \(\frac{1}{4}\) respectively. If all the three try to solve the problem independently, find the probability that the problem is solved. (C.B.S.E. 2019 C)
Solution:
Given: P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{3}\) and P(C) = \(\frac{1}{4}\)

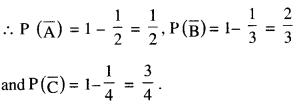
Probability that the problem is solved
= Probability that the problem is solved by at least one person
= 1 – \(\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\overline{\mathrm{B}}) \mathrm{P}(\overline{\mathrm{C}})\)
= 1 – \(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4}\)= 1 – \(\frac{1}{4}=\frac{3}{4}\)

Question 4.
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event “number is even” and B be the event “number is marked red”. Find whether the events A and B are independent or not. {Delhi 2019)
Solution:
Here, A : number is even i.e.,
A = {2,4,6}
and B : number is red i.e.,
B = {1,2,3}
∴ P(A) = \(\frac{3}{6}=\frac{1}{2}\) and P(B) = \(\frac{3}{6}=\frac{1}{2}\)
And,
P(A ∩ B) = P(Number is even and red) = \(\frac { 1 }{ 6 }\) .
Thus, P(A ∩ B) ≠ P(A). P(B)
[∵ \(\frac{1}{6} \neq \frac{1}{2} \times \frac{1}{2}\) ]
Hence, the events A and B are not indepedent.

Question 5.
A die is thrown 6 times. If “getting an odd number” is a success, what is the probability of (i) 5 successes (ii) at most 5 successes? (Delhi 2019)
Solution:
Probability of getting an odd number is one 3 1
trial = \(\frac{3}{6}=\frac{1}{2}\) = p ( say)
Probability of getting an even number in one 3
trial = \(\frac{3}{6}=\frac{1}{2}\) = g(say) o l
Also, n = 6.

(i) P(5 successes) = P(5) = ⁶C₅ q¹ p⁵
(ii) P(at most 5 successes)
= P(0) + P(1) + … + P(5) = 1 – P(6)
= 1 – ⁶C₆ q⁰ p⁶
= 1 – \(\frac{1}{64}=\frac{63}{64}\)

Question 6.
The random variable ‘X’ has a probability distribution P(X) of the following form, where ‘k’ is some number :
\(\mathbf{P}(\mathbf{X}=\boldsymbol{x})=\left\{\begin{array}{l}
\boldsymbol{k}, \text { if } \boldsymbol{x}=\mathbf{0} \\
2 k, \text { if } x=1 \\
3 k, \text { if } x=2 \\
0, \text { otherwise. }
\end{array}\right.\)
Determine the value of ‘P. (Outside Delhi 2019)
Solution:
We have : P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ k + 2k + 3k = 1
⇒ 6k = 1.
Hence, k = \(\frac { 1 }{ 6 }\).

Question 7.
Out of 8 outstanding students of a school, in which there are 3 boys and 5 girls, a team of 4 students is to be selected for a quiz competiton. Find the probability that 2 boj and 2 girls are selected. (Outside Delhi 2019)
Solution:
Read, probability = \(\frac{{ }^{3} \mathrm{C}_{2} \times{ }^{5} \mathrm{C}_{2}}{{ }^{8} \mathrm{C}_{4}}\)
= \(\frac{3 \times 10}{70}=\frac{3}{7}\)

Question 8.
12 cards numbered 1 to 12 (one number on one card), are placed in a box and mixed up thoroughly. Then a card is drawn at ran¬dom from the box. If it is known that the number on the drawn card is greater than 5, find the probability that the card bears an odd number. {Outside Delhi 2019)
Solution:
Let the events be as :
A : Card bears an odd number.
B : Number on the card is greater than 5.
A∩B = {7, 9, 11}.
Hence, P(A/B) = \(\frac{P(A \cap B)}{P(B)}\)
= \(\frac{3 / 12}{7 / 12}=\frac{3}{7}\)

Question 9.
The probability of solving a specific problem independently by A and B are \(\frac { 1 }{ 3 }\) and \(\frac { 1 }{ 5 }\) respectively. If both try to solve the problem independently, find the probability that the problem is solved.
(iOutside Delhi 2019)
Solution:
P (Problem is solved)
= 1 – P (Problem is not solved)
= 1 – \(\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\)
= 1 – \(\frac{2}{3} \times \frac{4}{5}\)
= 1 – \(\frac{8}{15}=\frac{7}{15}\)

Probability Important Extra Questions Long Answer Type 1

Question 1.
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4. (C.B.S.E. 2018)
Solution:
Let the events be as:
E : Sum of numbers is 8
F : Number of red die less than 4.
E : {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
F = {(1, 1), (2, 1), … (6, 1), (1, 2), (2, 2), … (6, 2), (1, 3), (2, 3), … (6, 2) (6, 3)}
and E ∩ F = {(5, 3), (6, 2)}
P(E) = \(\frac{5}{36}\), P(F) = \(\frac{18}{36}\)
and P(E ∩ F) = \(\frac{2}{36}\).
Hence, P(E/F) = \(\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}=\frac{2 / 36}{18 / 36}\)
= \(\frac{2}{18}=\frac{1}{9}\)

Question 2.
Two numbers are selected at random (with-out replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and vari-ance of X.
Solution:
The first five positive integers are 1, 2, 3, 4 and 5.
We select two positive numbers in 5 x 4 = 20 way.
Out of three, two numbers are selected at ran-dom.
Let ‘X’ denote the larger of the two numbers.
X can be 2, 3, 4 or 5.
∴ P (X = 2) = P (Larger number is 2)
{(1, 2), (2,1)} = \(\frac{2}{20}\)
Similarly, P(X = 3) = \(\frac{4}{20}\) ,
P(X = 4) = \(\frac{6}{20}\)
and P(X = 5) = \(\frac{8}{20}\)
Hence, the probability distribution is:

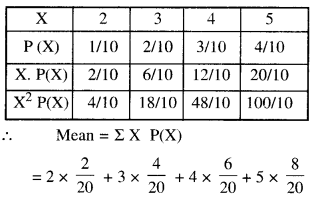
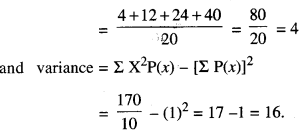
Question 3.
The probabilities of two students A and B coming to the school in time are \(\frac{3}{7}\) and \(\frac{5}{7}\) respectively. Assuming that the events, ‘A coming in time’ and ‘B coming in time’ are independent, find the probability of only one of them coming to the school in time. (A.I.C.B.S.E. 2013)
Solution:
We have : P(A) = Probability of student A coming to school in time = \(\frac{3}{7}\)
P(B) = Probability of student B coming to school in time = \(\frac{5}{7}\)
∴ \(\mathrm{P}(\overline{\mathrm{A}})=1-\frac{3}{7}=\frac{4}{7}\)
and \(\mathrm{P}(\overline{\mathrm{B}})=1-\frac{5}{7}=\frac{2}{7}\)
∴ Probability that only one of the students coming to school in time
= P(A ∩ \(\overline{\mathrm{B}}\)) + P( \(\overline{\mathbf{A}}\) ∩B)
= P(A)P(\(\overline{\mathrm{B}}\)) + P(\(\overline{\mathrm{B}}\))PB)
[∵ A and B are independent => A and \(\overline{\mathrm{B}}\) and \(\overline{\mathrm{A}}\) and B are also independent]
= \(\left(\frac{3}{7}\right)\left(\frac{2}{7}\right)+\left(\frac{4}{7}\right)\left(\frac{5}{7}\right)=\frac{26}{49}\)

Question 4.
A speaks truth in 80% cases and B speaks truth in 90% cases. In what percentage of cases are they likely to agree with each other in stating the same fact? (C.B.S.E. Sample Paper 2019-20)
Solution:
P(A) = \(\frac{80}{100}=\frac{4}{5}\)
and P( B) = \(\frac{90}{100}=\frac{9}{10}\)
P(\(\overline{\mathrm{A}}\)) = 1 – P(A) = 1 – \(\frac{4}{5}=\frac{1}{5}\)
P(\(\overline{\mathrm{B}}\)) = 1 – P(B) = 1 – \(\frac{9}{10}=\frac{1}{10}\)
∴ P(Agree) = P(Both speak the truth or both tell a lie)

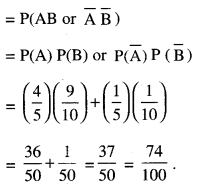
Hence, the reqd. percentage = 74%.

Question 5.
A problem in Mathematics is given to three students whose chances of solving it are \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\). What is the probability in the
following cases?
(i) that the problem is solved
(ii) only one of them solves it correctly
(iii) at least one of them may solve it.
Solution:
Let A, B, C be three events when a problem in
Mathematics is solved by three students.
Given : P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{3}\), P(C) = \(\frac{1}{4}\).
.-. P(A) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\), P(B) = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
and P(C) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

(i) Probability that the problem is solved = Probability that the problem is solved by at least one student

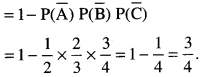
(ii) Probability that only one solves it correctly = P(Aninc)+P(AnBnc)+P(AnBnc)

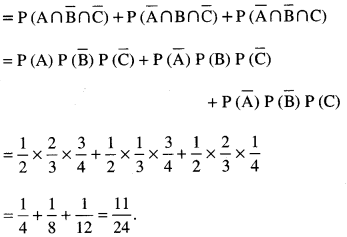
(iii) Probability that atleast one of them may solve the problem

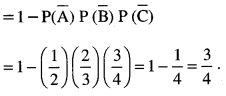
Question 6.
In a set of 10 coins, 2 coins with heads on both sides. A coin is selected at random from this set and tossed five times. Of all the five times, the result was head, find the probability that the selected coin had heads on both sides. (A.I. C.B.S.E. 2015)
Solution:
Let the events be :
E₁ : Selecting a coin with two heads
E₂ : Selecting a normal coin and A : The coin falls head all the times.
Since E₁ and E₂ are mutually exclusive and by the data given in the problem, we have :
P(E₁) = \(\frac{2}{10}=\frac{1}{5}\)
P(A/E₂) = \(\frac{8}{10}=\frac{4}{5}\) = P(A/E₁) = 1
P(A/E₁) = 1
P(A/E₂) = \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{32}\)
Now P(A) = P(A ∩ E₁) + P(A ∩ E₂)
= P(E₁) P(A/ E₁) + P(E₂) P(A/ E₂)
= \(\frac{1}{5}+\frac{1}{40}=\frac{8+1}{40}=\frac{9}{40}\)

Question 7.
A person playsa game of tossing a coin thrice. For each head he is given XI by the organiser of the game and for each tail he has to give ₹1.50 to the organiser. Let ‘X’ denote the amount gained or lost by the person. Show that ‘X’ is a random variable and exhibit it as a function on the sample space of the experiment. (N.C.E.R.T.)
Solution:
Since ‘X’ is a number whose values are defined by the outcomes of the random experiment,
∴ ‘X’ is a random variable.
Now sample space is given by :
S = {HHH, HHT, HTH, THH, HIT, THT, TTH, ITT},
where H = Head and T = Tail.
Thus X (HHH) = 2 x 3 = ₹6
X (HHT) = X (HTH) = X (THH)
= 2×2-lxl.5 = ₹ 2.50
X (HTT) = X (THT) = X (TTH)
= lx2-2xl.5 = -₹l
and X (TTT) = -(3xl.5) = – ₹4.50.
Thus for each element of S, X takes a unique value.
∴ ‘X’ is a function on the sample space S having range = {6, 2.50, – 1, – 4.50}.

Question 8.
Two numbers are selected at random (without replacement) from first 7 natural numbers. If X denotes the smaller of the two numbers obtained, find the probability distribution of X. Also, find mean of the distribution.
(C.B.S.E. Sample Paper 2019-20)
Solution:
Let ‘X’ be the smaller of the two numbers obtained.
Thus, X takes values 1, 2, 3, 4, 5 and 6.

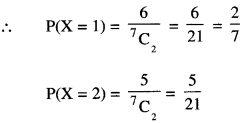
(ii) We have :

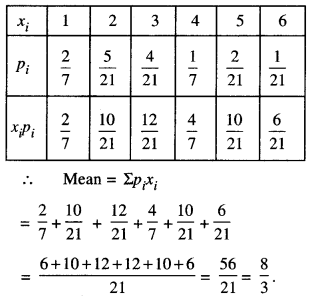
Question 9.
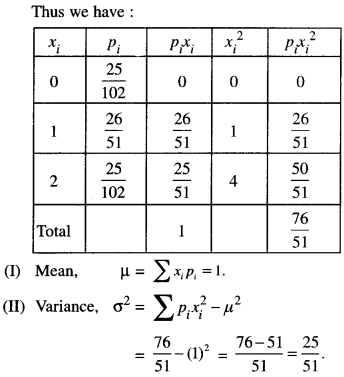
Two cards are drawn simultaneously (with-out replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of red cards. (A.I.C.B.S.E. 2012)
Solution:
Here ‘X’ takes values 0, 1, 2

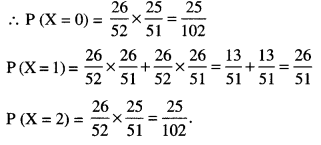
Question 10.
There is a group of 50 people who are patriotic out of which 20 believe in non-violence. Two persons are selected at random out of them, write the probability distribution for the selected persons who are non-violent. Also find the mean of the distribution.
Solution:
Let ‘X’ be the number of non-violent persons.
Here ‘X’ takes values 0, 1,2.
Thus no. of non-violent persons = 20
and no. of violent persons = 50 – 20 = 30.

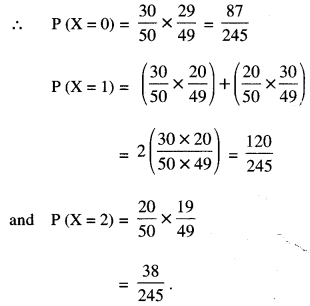
Hence, probability distribution is given by :

Question 11.
Two groups are competing for the positions of the Board of Directors of a corporation. The probabilities that the first and second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group. (C.B.S.E. 2018 C)
Solution:
Let E₁ = First group wins, E₂ = Second group wins
H = Introduction of new product.
P(E₁) = 0.6, P(E₂) = 0.4
P(H/E₂) = 0.3 P(H/E₁) = 0.7
Now,
P(E₂/H) = \(\frac{\mathrm{P}\left(\mathrm{E}_{2}\right) \mathrm{P}\left(\mathrm{H} / \mathrm{E}_{2}\right)}{\mathrm{P}\left(\mathrm{E}_{2}\right) \mathrm{P}\left(\mathrm{H} / \mathrm{E}_{2}\right)+\mathrm{P}\left(\mathrm{E}_{1}\right) \mathrm{P}\left(\mathrm{H} / \mathrm{E}_{1}\right)}\)

Question 12.
From a lot of 20 bulbs which include 5 defectives, a sample of 3 bulbs is drawn at random, one by one with replacement. Find the probability distribution of the number of defective bulbs. Also, find the mean of the distribution. (C.B.S.E. 2018 C)
Solution:
Let X denote the number of defective bulbs.
X = 0, 1, 2, 3.
P(X = 0) = \(\left(\frac{15}{20}\right)^{3}=\frac{27}{64}\)
P(X = 1) = \(3\left(\frac{5}{20}\right)\left(\frac{15}{20}\right)^{2}=\frac{27}{64}\)
P(X = 2) = \(3\left(\frac{5}{20}\right)^{2}\left(\frac{15}{20}\right)=\frac{9}{64}\)
P(X = 3 )=\(\left(\frac{5}{20}\right)^{3}=\frac{1}{64}\)
Mean = ΣXP(X) = \(\frac{27}{64}+\frac{18}{64}+\frac{3}{64}=\frac{3}{4}\)

Probability Important Extra Questions Long Answer Type 2

Question 1.
In a hockey match t wo teams A and B scored same number of goals upto the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternately and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match. (A.I.C.B.S.E. 2013)
Solution:
P(A), probability of A’s getting a six = \(\frac { 1 }{ 6 }\)
\(\mathrm{P}(\overline{\mathrm{A}})\), probability of A’s not getting a six
= 1 – \(\frac{1}{6}=\frac{5}{6}\)
Thus, P(A) = \(\frac{1}{6}\) \(\mathrm{P}(\overline{\mathrm{A}})\) = \(\frac{5}{6}\).
Similarly, P(B) = \(\frac{1}{6}\), \(\mathrm{P}(\overline{\mathrm{B}})\). = \(\frac{5}{6}\)

Question 2.
If A and B are two independent events such that:
\(\mathbf{P}(\overline{\mathbf{A}} \cap \mathbf{B})=\frac{2}{\mathbf{1 5}}\) and \(\mathbf{P}(\mathbf{A} \cap \overline{\mathbf{B}})=\frac{1}{\mathbf{6}}\), then find P(A) and P(B). (C.B.S.E. 2015)
Solution:
Since A and B are independent events,
\(\overline{\mathrm{A}}\) and B, A and \(\overline{\mathrm{B}}\) are also independent events.
Now \(P(\bar{A} \cap B)=\frac{2}{15}\) => \(\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\mathrm{B})=\frac{2}{15}\)
(1 – P(A)P(B) = \(\frac{2}{15}\)
P(B) – P(A))P(B) = \(\frac{2}{15}\) ………… (1)
And P(A∩\(\overline{\mathrm{B}}\))
P(A) \(\overline{\mathrm{B}}\) = \(\frac{1}{6}\)
P(A) (1 — P(B)) = \(\frac{1}{6}\)
P(A)-P(A)P(B) = \(\frac{1}{6}\) ………… (2)
Putting P(A) = x and P(B) = y in (1) and (2), we get
y – xy = \(\frac{2}{15}\)
and x – xy = \(\frac{1}{6}\) ………..(2)
Subtracting (2) from (1) y = y – x = \(\frac{2}{15}\) –\(\frac{1}{6}\)
⇒ y – x = \(\frac{-1}{30}\)
⇒ y = x – \(\frac{1}{30}\) ………… (3)
Putting in (1)’, \(x-\frac{1}{30}-x\left(x-\frac{1}{30}\right)=\frac{2}{15}\)
⇒ \(x-\frac{1}{30}-x^{2}+\frac{x}{30}=\frac{2}{15}\)
⇒ 30x – 1 – 30x² + x = 4
⇒ 30x² – 31x + 5 = 0.

If the girl tossed a coin .three times and exactly
1 tail shown, then: „ n
{HTH, HHT, THH} = 3
∴ P(A/E₁) = \(\frac { 3 }{ 8 }\)

Let A be the event that the girl obtained ex-actly one tail. If the girl tossed a coin only once and exactly 1 tail.
∴ P(A/E₂) = \(\frac { 1 }{ 2 }\)
By Bayes’ Theorem,

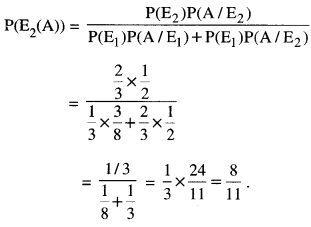
Question 6.
A manufacturer has three machine operators A, B and C. The first operator A produces 1 % of defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job 30% of the time and C on the job for 20% of the time. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by A?
(Delhi 2019)
Solution:
Let the events be as below :
E₁ : Item produced by machine A.
E₂ : Item produced by machine B.
E₃ : Item produced by machine C. and D : Item drawn is defective.
We have to find P (E₁/D).
Now P(E₂) = \(\frac{50}{100}=\frac{1}{2}\) ,
P(E₂) = \(\frac{30}{100}=\frac{3}{10}\)
and P (E₃) = \(\frac{20}{100}=\frac{1}{5}\)
Also P(D/E₁) = \(\frac{1}{100}\)
P(D/E₂) = \(\frac{5}{100}\), P(D/E₃) = \(\frac{7}{100}\)
By Bayes’ Theorem,
P(E₁/D) =

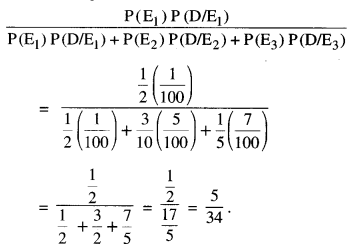
Question 7.
Bag I contain 3 white and 4 black balls, while Bag II contains 5 white and 3 black balls. One ball is transferred at random from Bag I to Bag II and then a ball is drawn at random from Bag II. The ball is drawn is found to be white. Find the probability that the transferred ball is also white.
(C.B.S.E. 2019 C)
Solution:
Let the events be as below:
E₁ : 1 white ball is transferred from Bag I to Bag II
E₂ : 1 black ball is transferred from Bag I to Bag II
and A: 1 white ball is drawn from Bag II.

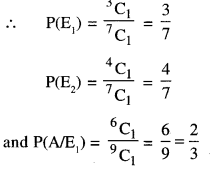
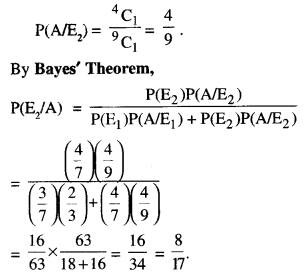
Question 8.
There are three coins. One is a two-headed coin (having head on both the faces), another is a biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of the three coins is chosen at random and tossed. If it shows head, what is the probability that it was the two-headed coin? (C.B.S.E. Sample Paper 2018-19)
Solution:
Let the events be:
E₁ : coin is two headed
E₂ : coin is biased and
E₃ : coin is unbiased.
And, A : coin shows up head.
∴P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\)
and P(A/E₁) = 1, P(A/E₂) = \(\frac{75}{100}=\frac{3}{4}\)
and P(A/E₃) = \(\frac{1}{2}\)
By Bayes’ Theorem,
P(E₁/A) =

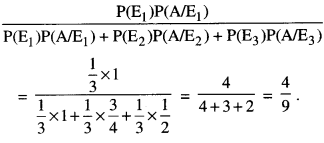
Hence, the required probability = \(\frac{4}{9}\)

Question 9.
Bag I contains 4 red and 2 green balls and Bag II contains 3 red and 5 green balls. One ball is transferred at random from Bag I to Bag II and then a ball is drawn at random from Bag II. The ball so drawn is found to be green in colour. Find the probability that the transferred ball is also green. (C.B.S.E. 2019 )
Solution:
Let the events be as below:
E₁ : 1 red ball is transferred from Bag I to Bag II
E₂ : 1 green ball is transferred from Bag I to Bag II
and A : 1 Green ball is drawn from Bag II.

Question 10.
There are three coins. One is a coin having tails on both faces, another is a biased coin that comes up tails 70% of the time and the third is an unbiased coin. One of the coins is chosen at random and tossed, it shows tail. Find the probability that it was a coin with tail on both the faces. (Outside Delhi 2019)
Solution:
Let the events be as below :
E₁ : Selected coin has tail on both faces
E₂ : Selected coin is biased
E₃ : Selected coin is unbiased and
A : Tail comes up.
Now P(E₁ ) = P(E₂ ) – P(E₃ ) = \(\frac{1}{3}\)

P(A/E₁) = 1,
P(A/E₂) = \(\frac{70}{100}=\frac{7}{10}\)
P(A/E₃) = \(\frac{1}{2}\)
By Bayes ’ Theorem :

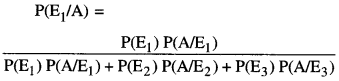
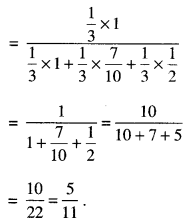
Question 11.
Let a pair of dice be thrown and the random variable ‘X’ be the sum of the numbers that appear on the two dice. Find the mean (or expectation) of X. (N.C.E.R.T.)
Solution:
Clearly the sample space consists of 36 elementary events = {(x_i, y_i) ; x_i, y_i = 1, 2,…., 6}.
X, the random variable = Sum of the numbers on the two dice.
∴ ‘X’ takes values 2, 3,4, or 12.

Now P(X = 2) = P({1,1}) = \(\frac{1}{36}\)
P (X = 3) = P ({1,2}, {2,1}) =\(\frac{2}{36}\)
P (X = 4) = P {(1,3), (2,2), (3,1)} = \(\frac{3}{36}\)
P (X = 5) = P {(1,4),(2,3), (3,2),(4,1)} = \(\frac{4}{36}\)
P (X = 6) = P {(1,5), (2,4), (3,3), (4,2), (5,1)} = \(\frac{5}{36}\)
P (X = 7) = P {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)} = \(\frac{6}{36}\)
P (X = 8) = P {(2,6), (3,5), (4,4), (5, 3), (6,2)} = \(\frac{5}{36}\)
P (X = 9) = P {(3,6), (4,5), (5,4), (6,3)} = \(\frac{4}{36}\)
P (X = 10) = P {(4, 6), (5,5), (6,4)} = \(\frac{3}{36}\)
P (X = 11) = P {(5,6), (6,5)} = \(\frac{2}{36}\)
P (X = 12) = P {(6, 6} = \(\frac{1}{36}\)
Thus the probability distribution is:

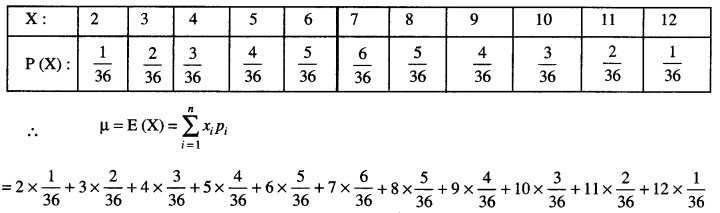
= \(\frac{1}{36}\)(2 + 6 + 12 + 20 + 30 + 42 + 40 + 36 + 30 + 22 + 12) = \(\frac{1}{36}\) (252) = 7.
Hence, the required, mean = 7.

Question 12.
Find the mean and variance of the numbers obtained on a throw of an unbiased die.
(N.C.E.R.T.)
Solution:
Here sample space, S = {1, 2, 3, 4, 5, 6}.
Let ‘X’ denote the number obtained on the throw.
Thus ‘X’ takes values 1, 2, 3, 4, 5 or 6.
∴ P (1) = P (2) = = P(6) = \(\frac{1}{6}\).
∴ Probability distribution is :

Question 13.
Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of kings. (C.B.S.E. Delhi 2019)
Solution:
Let X, number of kings = 0,1,2.
∴ P(X=0) = P (no king)
= \(\frac{48}{52} \times \frac{47}{51}=\frac{188}{221}\)
P(X = 1) = P (one king and one non-king)
= 2 x \(\frac{4}{52} \times \frac{48}{51}=\frac{32}{221}\)
P(X = 2) = P (two kings)
= \(\frac{4}{52} \times \frac{3}{51}=\frac{1}{221}\)
Hence, probability distribution is :

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 12 Linear Programming. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 12 Important Extra Questions Linear Programming

Linear Programming Important Extra Questions Very Short Answer Type

Question 1.
Draw the graph of the following LPP:
5x + 2y ≤ 10, x ≥ 0,y ≥ 0.
Solution:
Draw the line AB : 5.v + 2y = 10 …(1),
which meets x-axis at A (2, 0) and y-axis at B (0,5).
Also x = 0 is y-axis and y = 0 is x-axis.
Hence, the graph of the given LPP is as shown (shaded):

Question 2.
Solve the system of linear inequations: x + 2y ≤ 10; 2x + y ≤ 8.
Solution:
Draw the st. lines x + 2y = 10 and 2x + y = 8.
These lines meet at E (2,4).
Hence, the solution of the given linear inequations is shown as shaded in the following figure :

Question 3.
Find the linear constraints for which the shaded area in the figure below is the solution set:

Solution:
From the above shaded portion, the linear constraints are :
2x + y ≥ 2,x – y ≤ 1,
x + 2y ≤ 8, x ≥ 0, y ≥ 0.

Question 4.
A small firm manufactures neclaces and bracelets. The total number of neclaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a neclace. The maximum number of hours available per day is 16. If the profit on a neclace is ₹100 and that on a bracelet is ₹300. Formulate an LPP for finding how many of each should be produced daily to maximize the profit ?
It is being given that at least one of each must be produced. (C.B.S.E. 2017)
Solution:
Let ‘x’ neclaces and ‘y’ bracelets be manufactured per day.
Then LPP problem is:
Maximize Z = 100x+300y
Subject to the constraints : x + y ≤ 24,
(1) (x) + \(\frac { 1 }{ 2 }\)y ≤ l6,
i.e. 2x + y ≤ 32
and x ≥ 1
and y ≥ 1
i.e. x – 1 ≥ 0
and y – 1 ≥ 0.

Question 5.
Old hens can be bought for ?2.00 each and young ones at ?5.00 each. The old hens lay 3 eggs per week and the young hens lay 5 eggs per week, each egg being worth 30 paise. A hen costs ₹1.00 per week to feed. A man has only ₹80 to spend for hens. Formulate the problem for maximum profit per week, assuming that he cannot house more than 20 hens.
Solution:
Let ‘x’ be the number of old hens and ‘y’ the number of young hens.
Profit = (3x + 5y) \(\frac { 30 }{ 100 }\) – (x + y) (1)
= \(\frac{9 x}{10}+\frac{3}{2}y\)x – y
= \(\frac{y}{2}-\frac{x}{10}=\frac{5 y-x}{10}\)
∴ LPP problem is:
Maximize Z = \(\frac{5 y-x}{10}\) subject to:
x ≥ 0,
y ≥ 0,
x + y ≤ 20 and
2x + 5y ≤ 80.

Linear Programming Important Extra Questions Very Long Answer Type 2

Question 1.
Maximize Z-5x + 3y
subject to the constraints:
3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0,y ≥ 0. (N.C.E.R.T)
Solution:
The system of constraints is :
3x + 5y ≤ 15 …(1)
5x + 2y ≤ 10 …(2)
and x ≥ 0, y≥ 0 …(3)
The shaded region in the following figure is the feasible region determined by the system of constraints (1) – (3):

It is observed that the feasible region OCEB is bounded. Thus we use Corner Point Method to determine the maximum value of Z, where :
Z = 5x + 3y …(4)

The co-ordinates of O, C, E and B are (0, 0), (2,0), \(\left(\frac{20}{19}, \frac{45}{19}\right)\) (Solving 3x + 5y = 15 and 5x + 2y – 10) and (0, 3) respectively.
We evaluate Z at each comer point:

Hence’ Z_max = at the Point \(\left(\frac{20}{19}, \frac{45}{19}\right)\)

Question 2.
Minimize Z = 3x + 2y subject to the constraints:
x +y ≥ 8, 3x + 5y ≤ 15, x ≥ 0, y ≥ 0. (N.C.E.R.T.)
Solution:
The system of constraints is :
x +y ≥ 8, , x ≥ 0, y ≥ 0…(1)
3x + 5y ≤ 15 …(2)
and x ≥ 0, y ≥ 0 …(3)

It is observed that there is no point, which satisfies all (1) – (3) simultaneously.
Thus there is no feasible region.
Hence, there is no feasible solution.

Question 3.
Determine graphically the minimum value of the objective function :
Z = – 50x + 20y
subject to the constraints:
2x-y ≥ – 5, 3x +y ≥ 3, 2x – 3y ≤ 12, x,y ≥ 0. (N.C.E.R.T.)
Sol. The system of constraints is :
2x-y ≥ – 5 …(1)
3x +y ≥ 3 …(2)
2x – 3y ≤ 12 …(3)
and x,y ≥ 0 …(4)
The shaded region in the following figure is the feasible region determined by the system of constraints (1) – (4).

It is observed that the feasible region is unbounded.
We evaluate Z = – 50x + 20y at the corner points :
A (1, 0), B (6, 0), C (0, 5) and D (0, 3) :

From the table, we observe that – 300 is the minimum value of Z.
But the feasible region is unbounded.
∴ – 300 may or may not be the minimum value of Z. ”

For this, we draw the graph of the inequality.
– 50x + 20y < – 300
i.e. – 5x + 2y < – 30.
Since the remaining half-plane has common points with the feasible region,
∴ Z = – 50x + 20y has no minimum value.

Question 4.
Minimize and Maximize Z = 5x + 2y subject to the following constraints : x – 2y ≤ 2, 3x + 2y < 12, -3x + 2y ≤ 3, x ≥ 0, y ≥ 0. (A.I.C.B.S.E. 2015)
Solution:
The given system of constraints is :
x – 2y ≤ 2 …(1)
3x + 2y < 12 …(2)
-3x + 2y ≤ 3 …(3)
and x ≥ 0, y ≥ 0.

The shaded region in the above figure is the feasible region determined by the system of constraints (1) – (4). It is observed that the feasible region OAHGF is bounded. Thus we use Corner Point Method to determine the maximum and minimum value of Z, where
Z = 5x + 2y …(5)

The co-ordinates of O, A, H, G and F are :
(0, 0). (2. 0), (\(\frac{7}{2}, \frac{3}{4}\)) and (\(\frac{3}{2}, \frac{15}{4}\)), \(\frac { 3 }{ 2 }\))
respectively. [Solving x

2y = 2 and 3x + 2y = 12 for
H and -3x + 2y = 3 and
3x + 2y = 12 for G]
We evaluate Z at each cormer point:

Hence, Z_max = 19 at (\(\frac{7}{2}, \frac{3}{4}\)) and
Z_max = 0at (0,0)

Question 5.
A dealer in rural area wishes to purchase a number of sewing machines. He has only ₹5760.00 to invest and has a space for at most 20 items. An electronic sewing machine costs him ₹360.00 and a manually operated sewing machine ₹240.00. He can sell electronic sewing machine at a profit of ₹22.00 and a manually operated sewing machine at a profit of ₹18.00. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit. Make it a linear programming problem and solve it graphically. (C.B.S.E. 2014)
Solution:
Let ‘x’ be the number of electronic operated machines and ‘y’ that of manually operated machines be purchased.
Then the LPP problem is as follows :
Maximize:
Z = 22 + 18y
Subject to:
x + y ≤ 20 …(1)
360x + 240y ≤ 5760
i.e. 3x + 2y ≤ 48 …(2)
and x ≥ 0, y ≥ 0 …(3)
The shaded region of the figure represents the feasible region OCEB, which is bounded.

Applying Corner Point Method, we have:

Thus, Z is maximum at E (8, 12).
Hence, the dealer should invest in 8 electronic and 12 manually operated machines.

Question 6.
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 35 per package of nuts and ₹ 14 per package of bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day? Convert it into an LPP and solve graphically.
Solution:
Let ‘x’ and ‘y’ be the number of packages of nuts and bolts respectively.
We have the following constraints :
x ≥ 0 …(1)
y ≥ 0 …(2)
x + 3y ≤ 12 ….(3)
3x + y ≤ 12 …(4)
Now the profit,P= 35x+ 14y …..(5)
We are to maximize P subject to constraints (1) -(4).
Draw the line AB (x + 3y = 12)
Draw the line CD (3x + y = 12)
These meet at E (3, 3).
The shaded region in the figure represents the feasible region, which is bounded.

Applying Corner Point Method, we have :

Hence, max. profit is ₹ 147 and it is obtained when 3 packages each of Nuts and Bolts are produced daily.

Question 7.
Two tailors A and B earn ₹ 150 and ₹ 200 per day respectively. A can stitch 6 shirts and 4 pants per day, while B can stitch 10 shirts and 4 pants per day. Form a L.P.P. to minimize the labour cost to produce (stitch) at least 60 shirts and 32 pants and solve it graphically.
Solution:
Let the tailor A work for ‘x’ days and B for ‘y’ days.

Thus, we have the following constraints:
x ≥ 0 …(1)
y ≥ 0 …(2)
6x + 10y ≥ 60
i.e. 3x + 5y ≥ 30 …….(3)
4x + 4y ≥ 32
i.e. x + y ≥ 8 ……(4)
The objective function, or the cost Z is:
Z = 150x + 200 y ……..(5)
For the solution set, we draw the lines:
x = 0, y – 0, 3x + 5y = 30, x + y = 8

The feasible region (shaded) is unbounded. Let us evaluate Z at the comer points:
A (10,0), D(0, 8) and E(5, 3)
[Solving x + y – 8, Sx + 5y – 30; x – 5,y = 3]

Applying Comer Point Method, we have:

Hence, the tailor A should work for 5 days and B for 3 days.
To Check: Draw 150x + 200y < 1350 i.e. 3x + 4y < 27.
Since there is no region common with feasible region,
∴ Minimum value is ₹ 1350.

Question 8.
A dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. It costs ₹50 per kg to produce food I. Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C and it costs ₹70 per kg to produce food n. Formulate this problem as a LPP to minimise the cost of a mixture that will produce the required diet. Also find the minimum cost
Solution:
Let the quantity of Food I = x kg
and the quantity of Food II = y kg.
Then the LPP problem is as below :
Z = 50x+70y …(1)
Subject to 2x + y ≥ 8 …(2)
x + 2y ≥ 10 ….(3)
and x ≥ 0, y ≥0 ……..(4)
For the solution, we draw the lines :
x = 0,y = 0,2x + y = 8 and x + 2y = 10

The feasible regin is as shown with vertices C(10,0), E(2,4) and B(0,8).
Applying Corner Point Method, we have

Thus minimum cost is ₹38Q when 2 kg of Food I and 4 kg of Food II are mixed.

Question 9.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

The machines I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively. The profit on each toy of type A is ₹50 and that of type Bis ₹60. Formulate the above problem as a LPP and solve it graphically to maximize profit.
(C.B.S.E. Sample Paper 2018-19)
Solution:
Let ‘x’ and ‘y’ be the number of toys of type A and type B respectively.
Then maximize :
P = 50x + 60y …(1)
Subject to constraints :
20x +10v ≤ 180 …(2)
10x + 20y ≤ 120 …….(3)
10x + 30y ≤ 150 ……(4)
and x ≥ 0, y ≥ 0 …(5)

Applying Corner Point Method we have :

Hence, maximum profit is ₹520 when x = 8 and y = 2. i.e., when 8 toys of type A and 2 toys of type B are made.

Question 10.
A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand- operated. It takes 4 minutes on the automatic and 6 minutes on the hand operated machines to manufacture a packet of screws ‘A’ while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a packet of screws ‘B\ Each machine is available for at most 4 hours on any day. The manufactures can sell a packet of screws ‘A’ at a profit of 70 paise and screws ‘B’ at a profit of ₹ 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it graphically and find the maximum profit (C.B.S.E. 2018)
Solution:
Let the factory manufacture ‘x’ of type ‘A’ and ‘y’ of type ‘B’
Clearly x ≥ 0 …(1)
and y ≥ 0 …(2)
Since the machines can operate for at the most 4 hours a day,
4x + 6y ≤ 240
i.e., 2x + 3y ≤ 120 …(3)
and 6x + 3y ≤ 240
i.e., 2x + y ≤ 80 …(4)
The objective function or the profit, P, is:
P = 0.7 x + y …(5)

We drawn the lines :
x = 0,y = 0,
2x + 3y = 120
and 2x + y – 80

The feasible region is shown shaded OCPB is bounded, where O is (0, 0), C is (40, 0), B is (0, 40) and P is (30, 20).
[Solving 2x + y – 80 and 2x + 3y = 120; x = 30, y – 20]

Applying Corner Point Method, we have :

Hence, in order to maximize profit 30 packets of screw ‘A’ and 20 packets of screw ‘B’ should be manufactured and maximum profit = ₹ 41.

Question 11.
A small firm manufactures chairs and tables. Market demand and available resources indicate that the continued production of chairs and tables should not exceed 50 units per day. It takes 30 minutes to manufacture a chair and 1 hour to manufacture a table. A maximum of 40 man-hours per day are available. The profit on each chair is ₹ 40 and profit on each table is ₹ 60. Determine how many each of chairs and tables should be manufactured per day in order to maximize the profit. What is the maximum profit? Formulate LPPand solve graphically.
Solution:
Let ‘x’ and ‘y’ be the number of chairs and tables respectively.
We have: x ≥ 0 ………..(1)
y ≥ 0 ………(2)
x + y ≤ 50 ……(3)
and \(\frac{x}{2}\) + y ≤ 40
⇒ x + 2y < 80 …(4)
The objective function, or the profit, Z is
Z = 40 x + 60 y …(5)

We have to maximize Z subject to (1) – (4).
For solution set, we draw the lines:
x = 0, y – 0, x + y = 50 and x + 2y – 80.
The lines x + y = 50 and x + 2y = 80 meet at E (20, 30).

The shaded portion represents the feasible region, which is bounded.
Applying Corner Point Method, we have:

Hence, the maximum profit is ₹ 2600 when 20 chairs and 30 table are manufactured.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 11 Three Dimensional Geometry. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 11 Important Extra Questions Three Dimensional Geometry

Three Dimensional Geometry Important Extra Questions Very Short Answer Type

Question 1.
Find the acute angle which the line with direction-cosines \(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{6}}, n>\) makes with positive direction of z-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
l² + m² + n² = 1
\(\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{6}}\right)^{2}\) + n² = 1
⇒ \(\frac{1}{3}+\frac{1}{6}\) + n² = 1
n² = 1 – \(\frac{1}{2}\)
n² = \(\frac{1}{2}\)
n = \(\frac{1}{\sqrt{2}}\)
Thus, cos α = \(\frac{1}{\sqrt{2}}\)
Hence, α = 45° or \(\frac{\pi}{4}\)

Question 2.
Find the direction-cosines of the line.
\(\frac{x-1}{2}=-y=\frac{z+1}{2}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given line is \(\frac{x-1}{2}=\frac{y}{-1}=\frac{z+1}{2}\)
Its direction-ratios are <2,-1,2>.
Hence, its direction- cosine are:

Question 3.
If α, β, γ are direction-angles of a line, prove that cos 2a + cos 2P + cos 2y +1 = 0. (N.C.E.R.T.)
Solution:
Since α, β, γ are direction-angles of a line,
∴ cos² α + cos² β + cos²γ = 1

⇒ 1 + cos2α + 1 + cos2β + 1 + cos2γ = 2
⇒ cos 2α + cos 2β + cos 2γ + 1 = 0, which is true.

Question 4.
Find the length of the intercept, cut off by the plane 2x + y – z = 5 on the x-axis.   (C.B.S.E. Outside Delhi 2019)
Solution:
The given plane is2x + y – z = 5
⇒ \(\frac{x}{5 / 2}+\frac{y}{5}+\frac{z}{-5}=1\)
Its intercepts are \(\frac{x}{5 / 2}\), 5 and -5.
Hence, the length of the intercept on the x-axis is \(\frac{x}{5 / 2}\)

Question 37.
Find the length of the perpendicular drawn from the point P(3, -4,5) on the z-axis.
Solution:
Length of the perpendicular from P(3, -4,5) on the z-axis
= \(\sqrt{(3)^{2}+(-4)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5 units.

Question 5.
Find the vector equation of a plane, which is at a distance of 5 units from the origin and whose
normal vector is \(2 \hat{i}-\hat{j}+2 \hat{k}\)
Solution:
Let \(\vec{n}=2 \hat{i}-\hat{j}+2 \hat{k}\)

Question 6.
If a line makes angles 90°, 135°, 45° with the x,y and z-axes respectively, find its direction cosines.
Solution:
Direction cosines of the line are :
< cos 90°, cos 135°, cos 45° >
<0, \(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\)>

Question 7.
Find the co-ordinates of the point where the line through the points A (3,4,1) and B (5,1, 6) crosses the xy-plane.
The equations of the line through A (3,4,1) and B (5,1,6) are:

Any point on (1) is (3 + 2k,4- 3k, 1 + 5k) …………. (2)
This lies on xy-plane (z = 0).
∴ 1 + 5k = 0 ⇒ k = \(-\frac{1}{5}\)
Putting in (2), [ 3-\(\frac{2}{5}\), 4 + \(\frac{3}{5}\), 1-1)
i.e. (\(\frac{13}{5}\), \(\frac{23}{5}\), 0)
which are the reqd. co-ordinates of the point.

Question 8.
find the vector equation ofthe line which passes through the point (3,4,5) and is parallel to the vector \(2 \hat{i}+2 \hat{j}-3 \hat{k}\)
Solution:
The vector equation of the line is \(\vec{r}=\vec{a}+\lambda \vec{m}\)
i.e., \(\vec{r}=(3 \hat{i}+4 \hat{j}+5 \hat{k})+\lambda(2 \hat{i}+2 \hat{j}-3 \hat{k})\)

Three Dimensional Geometry Important Extra Questions Short Answer Type

Question 1.
Find the acute angle between the lines whose direction-ratios are:
< 1,1,2 > and <-3, -4,1 >.
Solution:

Question 2.
Find the angle between the following pair of lines:
and
\(\frac{-x+2}{-2}=\frac{y-1}{7}=\frac{z+3}{-3}\) and \(\frac{x+2}{-1}=\frac{2 y-8}{4}=\frac{z-5}{4}\)
and check whether the lines are parallel or perpendicular. (C.B.S.E. 2011)
Solution:
The given lines can be rewritten as :
\(\frac{-x+2}{-2}=\frac{y-1}{7}=\frac{z+3}{-3}\) ………….. (1)
\(\frac{x+2}{-1}=\frac{2 y-8}{4}=\frac{z-5}{4}\) ………..(2)
Here < 2,7, – 3 > and < -1,2,4 > are direction- ratios of lines (1) and (2) respectively.

Hence, the given lines aife perpendicular.

Question 3.
Find the vector equation of the line joining (1.2.3) and (-3,4,3) and show that it is perpendicular to the z-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
Vector equation of the line passing through
(1.2.3) and(-3,4,3)is \(\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})\)
where \(\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}\) and \(\vec{b}=-3 \hat{i}+4 \hat{j}+3 \hat{k}\)
⇒ \(\vec{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-4 \hat{i}+2 \hat{j})\) …(1)
Equation of z-axis is \(\vec{r}=\mu \hat{k}\) …(2)
Since \((-4 \hat{i}+2 \hat{j}) \cdot \hat{k}=0\) = 0,
∴ Line (1) is perpendicular to z-axis.

Question 4.
Find the vector equation of the plane, which is \(\frac{6}{\sqrt{29}}\) at a distance of
units from the origin and its normal vector from the origin is \(2 \hat{i}-3 \hat{j}+4 \hat{k}\) . Also, find its cartesian form. (N.C.E.R.T.)
Solution:

Question 5.
Find the direction-cosines of the unit vector perpendicular to the plane \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) +1 = 0 through the origin. (N.C.E.R.T.)
Solution:
The given plane is \(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) + 1 = 0
\(\vec{r} \cdot(6 \hat{i}-3 \hat{j}-2 \hat{k})\) = 1 ………… (1)
Now \(|-6 \hat{i}+3 \hat{j}+2 \hat{k}|=\sqrt{36+9+4}\)
\(=\sqrt{49}=7\)
Dividing (1) by 7,
\(\vec{r} \cdot\left(-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\right)=\frac{1}{7}\)
which is the equation of the plane in the form \(\vec{r} \cdot \hat{n}=p\)
Thus, \(\hat{n}=-\frac{6}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{2}{7} \hat{k}\)
which is the unit vector perpendicular to the plane through the origin.
Hence, the direction-cosines of \(\hat{n}\) are \(<-\frac{6}{7}, \frac{3}{7}, \frac{2}{7}>\)

Question 6.
Find the acute angle between the lines
\(\frac{x-4}{3}=\frac{y+3}{4}=\frac{z+1}{5}\) and \(\frac{x-1}{4}=\frac{y+1}{-3}=\frac{z+10}{5}\)
Solution:
Vector in the direction of first line
\(\frac{x-4}{3}=\frac{y+3}{4}=\frac{z+1}{5}\) ,
\(\vec{b}=(3 \hat{i}+4 \hat{j}+5 \hat{k})\)

Vector in the direction of second line
\(\frac{x-1}{4}=\frac{y+1}{-3}=\frac{z+10}{5}\) ,
\(\vec{d}=4 \hat{i}-3 \hat{j}+5 \hat{k}\)
∴ θ, the angle between two given lines is given by:

Question 7.
Find the angle between the line:
\(\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-\hat{j}+3 \hat{k})\) and the plane \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})=4\) Also, find whether the line is parallel to the plane or not .
Solution:
The given line is :
\(\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda(2 \hat{i}-\hat{j}+3 \hat{k})\)
and the given plane is \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) = 4.
Now the line is parallel to 2\(\hat{i}\) – \(\hat{j}\) + 3\(\hat{k}\) and nor¬mal to the plane 2\(\hat{i}\) + \(\hat{i}\) – \(\hat{k}\)
If ‘θ’ is the angle between the line and the plane,
then \(\left(\frac{\pi}{2}-\theta\right)\) is the angle between the line and normal to the plane.
Then

Hence, the line is parallel to the plane.

Question 8.
Find the value of ‘λ’, so that the lines:
\(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2}\) and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) are at right angles. Also, find whether the lines are intersecting or not
Solution:
(i) The given lines are
\(\frac{1-x}{3}=\frac{7 y-14}{\lambda}=\frac{z-3}{2}\) ……………….(1)
and \(\frac{7-7 x}{3 \lambda}=\frac{y-5}{1}=\frac{6-z}{5}\) ……….. (2)
These are perpendicular if:

Hence λ = 1.

(ii) The direction cosines ofline(1) are <-3,1,2>
The direction cosines of line (2) are < -3,1, -5 >
Clearly, the lines are intersecting.

Question 9.
Find the angle between the line: \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) and the plane: 3x + 4y + z + 5 = 0.
x-2 y+1 z-3
Sol. The given line is \(\frac{x-2}{3}=\frac{y+1}{-1}=\frac{z-3}{-2}\) ………..(1)
and the given plane is :
3x + 4y + z + 5 = 0 …(2)
If the line (1) makes an angle ‘0’ with the plane (2), then the line (1) will make angle (90° – 0) with the normal to the plane (2).
Now direction-ratios of line (1) are:
<3, -1,-2>
and direction-ratios of normal to plane (2) are <3,4,1>.
∴ cos (90° – θ)

Question 10.
State when the line \(\vec{r}=\vec{a}+\lambda \vec{b}\) is parallel to the plane \(\vec{r} \cdot \vec{n}=\vec{d}\) . Show that the line \(\vec{r}=\hat{i}+\hat{j}+\lambda(\hat{2}+\hat{j}+4 \hat{k})\) is parafiel to the plane \(\vec{r} \cdot(-2 \hat{i}+\hat{k})\) = 5. Also, find the distance between the line and the plane.
Solution:
(i) A line is parallel to the plane if it is perpendicular to the normal to the plane.
The given line is \(\vec{r}=\vec{a}+\lambda \vec{b}\)
⇒ \(\vec{b}\) is parallel to the line.
The given plane is \(\vec{r} \cdot \vec{n}=\vec{d}\)

⇒ \(\vec{n}\) is normal to the plane.
Thus the line is parallel to the plane when
\(\vec{b} \cdot \vec{n}\) =0.

(ii) Here \(\vec{b}=2 \hat{i}+\hat{j}+4 \hat{k}\) and \(\vec{n}=-2 \hat{i}+\hat{k}\)
Now \(\vec{b} \cdot \vec{n}\) = (2) (- 2) + (1) (0) + (4) (1)
= -4 + 0 + 4 = 0.
Hence, the given line is parallel to the given plane.

(iii) (1,1,0) is a point on the given line.
Equation of the plane is-2x + z- 5= 0.
∴ Reqd. distance
= \(\left|\frac{-2(1)+0-5}{\sqrt{4+0+1}}\right|=\frac{7}{\sqrt{5}}=\frac{7 \sqrt{5}}{5}\)units.

Three Dimensional Geometry Important Extra Questions Very Long Answer Type 2

Question 1.
Find the shortest distance between the lines:\(\vec{r}=(4 \hat{i}-\hat{j})+\lambda(\hat{i}+{2} \hat{j}-{3} \hat{k})\) and \(\vec{r}=(\hat{i}-\hat{j}+2 \hat{k})+\mu(2 \hat{i}+4 \hat{j}-5 \hat{k})\) (C.B.S.E. 2018)
Solution:
Comparing given equations with:

Question 2.
A line makes angles α, β, γ, δ with the four diagonals of a cube, prove that:
cos² α + cos² β + cos² γ + cos² δ= \(\frac{4}{3}\). (N.C.E.R.T.)
Solution:
Let O be the origin and OA, OB, OC (each = a) be the axes.

Thus the co-ordinates of the points are :
O (0,0,0), A (a, 0,0), B (0, a, 0), C (0,0, a),
P (a, a, a), L (0, a, a), M (a, 0, a), N (a, a, 0).
Here OP, AL, BM and CN are four diagonals.
Let < l, m, n > be the direction-cosines of the given line.

Now direction-ratios of OP are:
<a-0,a-0,a-0>i.e.<a,a,a>
i.e. < 1,1,1 >,
direction-ratios of AL are:
<0-a, a-0, a-0> i.e. <-a,a,a>
i.e. <-l, 1,1 >,
direction-ratios of BM are:
<a-0,0-a, a-0>
i.e. <a,-a,a> i.e. < 1,-1, 1 >
and direction-ratios of CN are:
<a-0,a-0,0-a> i.e. <a,a,-a>
i.e. < 1,1,-1 >.

Thus the direction-cosines of OP are :
\(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
the direction-cosines of AL are:
\(<-\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
the direction-cosines of BM are :
\(<\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}>\)
and the direction-cosines of CN are :
\(<\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}>\)
If the given line makes an angle ‘a’ with OP, then :

and cos δ = \(\frac{|l+m-n|}{\sqrt{3}}\) ………… (4)
Squaring and adding (1), (2), (3) and (4), we get:
cos² α + cos² β + cos² γ + cos²δ
= \(\frac { 1 }{ 3 }\) [(l + m + n)² + (-l + m + n)²
+ (l-m + n)² + (l + m — n)²]
= \(\frac { 1 }{ 3 }\) [4(l² + m² + n²)] = \(\frac { 1 }{ 3 }\) [4(1)].
Hence,cos² α + cos² β + cos² γ + cos²δ = \(\frac { 4 }{ 3 }\)

Question 3.
Find the equation of the plane through the line \(\frac{x-1}{3}=\frac{y-4}{2}=\frac{z-4}{-2}\) and parallel to the line:
\(\frac{x+1}{2}=\frac{1-y}{4}=\frac{z+2}{1}\)
Hence, find the shortest distance between the lines. (C.B.S.E. Sample Paper 2018-19)
Solution:
The two given lines are:
\(\frac{x-1}{3}=\frac{y-4}{2}=\frac{z-4}{-2}\) ………… (1)
and \(\frac{x+1}{2}=\frac{1-y}{4}=\frac{z+2}{1}\) ………….. (2)
Let <a, b, c> be the direction-ratios of the normal to the plane containing line (1).
∴ Equation of the plane is:
a(x- l) + b(y-4) + c(z-4) …(3),
where 3a + 2b – 2c = 0 …(4)
[∵ Reqd. plane contains line (1)] and 2a – 4b + 1.c = 0
[∵ line (1) a parallel to the reqd. plane] Solving (4) and (5),

Putting in (3),
6k(x- 1) + 7k(y – 4) + 16k(z – 4) = 0
= 6(x – 1) + 7(y – 4) + 16(z – 4) =0
[∵k ≠ 0]
⇒ 6x + 7y+ 16z-98 = 0,

which is the required equation of the plane.
Now, S.D. between two lines = perpendicular distance of (-1,1, – 2) from the plane

6(—1) + 7(1) +16(-2) – 98
V(6)2+(7)2+(16)2
-6 + 7-32-98 V36 + 49 + 256

Question 4.
Find the Vector and Cartesian equations of the plane passing through the points (2, 2, -1), (3,4,2) and (7,0,6). Also, find the vector equa¬tion of a plane passing through (4,3,1) and parallel to the plane obtained above. (C.B.S.E. 2019)
Solution:
(i) Cartesian equations
Any plane through (2,2, -1) is :
a(x – 2) + b(y- 2) + c(z + 1) = 0 … (1)
Since the plane passes through the points (3,4,2) and (7,0,6),
∴ a(3 – 2) + b(4 – 2) + c(2 +1) = 0
and a(7 – 2) + b(0 – 2) + c(6 + 1) = 0
⇒ a + 2b + 3c = 0 …(2)
and 5a – 2b + 7c = 0 …(3)
Solving (2) and (3),\(\frac{a}{14+6}=\frac{b}{15-7}=\frac{c}{-2-10}\)
⇒ \(\frac{a}{20}=\frac{b}{8}=\frac{c}{-12}\)
⇒ \(\frac{a}{5}=\frac{b}{2}=\frac{c}{-3}\) = k (say), value k ≠ 0.
∴ a = 5k,b = 2k and c = -3k,
Putting the values of a, b, c in (1), we get:
5k(x – 2) + 2k(y – 2) – 3k(z + 1) = 0
⇒ 5(x-2) + 2(y-2)-3(z+ 1) =0[∵ k ≠ 0]
=» 5x- 10 + 2y-4-3z-3 = 0
=» 5x + 2y-3z-17 = 0, …(4)
which is the reqd. Cartesian equation.
Its vector equation is \(\vec{r} \cdot(5 \hat{i}+2 \hat{j}-3 \hat{k})\) =17.

(ii) Any plane parallel to (4) is
5x + 2y – 3z + λ – 0 … (5)
Since it passes through (4, 3,1),
5(4) + 2(3) – 3(1) + λ = 0
⇒ 20 + 6 — 3 + λ = 0
⇒ λ = -23.
Putting in (5), 5x + 2y – 3z – 23 = 0, which is the reqd. equation.
Its vector equation is \(\vec{r} \cdot(5 \hat{i}+2 \hat{j}-3 \hat{k})\) = 23.

Question 5.
Find the co-ordinates of the foot of the perpendicular drawn from the point A (1,8,4) to the line joining B (0, -1,3) and C (2,-3,-1). (A.I.C.B.S.E. 2016)
Solution:
Any point on BC, which divides [BC] in the ratio k: 1,is:

This becomes M, the foot of perp. from A on BC
if AM⊥BC …(2)
But direction-ratios of BC are:
<2-0,- 3 + 1,-1 -3 > i.e. < 2,-2,-4 >
i.e, <1, -1 > -2>
and direction-ratio of AM are:
\(<\frac{2 k}{k+1}-1, \frac{-3 k-1}{k+1}-8, \frac{-k+3}{k+1}-4>\)
i.e. < k- 1,- 11k:-9, -5k— 1 >
∴ Due to (2), (1) (k- 1) + (- 1) (-1 1k-9) + (-2)(-5k- 1) = 0
⇒ k – 1 + 11k + 9 + 10k + 2 = 0
⇒ 22k + 10 = 0
⇒ k = \(-\frac{5}{11}\)
∴ From (1), the co-ordinates of M, the foot of perp. are:

Question 6.
(a) Find the image of the point (1,6,3) in the line:
\(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\)
(C.B.S.E. 2010 C)
(b) Also, write the equation of the line joining the given point and its image and find the length of the segment joining the given point and its image. (C.B.S.E. 2010 C)
Solution:
(a) Let P be the given point (1, 6, 3) and M, the foot of perpendicular from P on the given line AB:

Any point on the given line is:
(k, 1+2k, 2+3k)
For some value of k, let the point be M.
∴ Direction-ratios of PM are:
<k-1,1+2k-6, 2 + 3k – 3> i.e. .
Since PM ⊥AB ,
∴ (1) (k-1) + (2)(2k-5) + (3) (3k-1) = 0
⇒ k-l +4k – 10 + 9&-3 = 0
⇒ 14 k = 14
⇒ k = 1.

∴ Foot of perpendicular M is (1,1 + 2,2 + 3) i.e. (1,3,5).
Let P'(α, β, γ) be the image of P in the given line. Then M is the mid-point of [PP’].
∴ \(\)
⇒α + 1 = 2, β + 6 = 6, γ+3 = 10
⇒ α = 1, β = 0, γ = 7.
Hence, the reqd. image is (1,0,7).

(b) (i) The equations of the line PP’ are :

(ii) Length of segment [PP’]

Question 7.
Find the co-ordinates of the foot of perpendicu¬lar and the length of the perpendicular draw n from the point P (5,4,2) to the line:
\(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\)
Also, find the image of P in this line. (A.I.C.B.S.E. 2012)
Solution:
(i) The given line is :
\(\vec{r}=-\hat{i}+3 \hat{j}+\hat{k}+\lambda(2 \hat{i}+3 \hat{j}-\hat{k})\)
i.e, \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) …………… (1)
The given point is P (5,4,2).

Let M be the foot of perpendicular from P on the given line AB.
Any point on (1) is (-1 + 2k, 3 +3k, l – k).
For some value of k, let the point be M.
Direction-ratios of PM are:
<-1+2k-5, 3+3k-4, 1-k-2>
i.e, <2k – 6, 3k – 1, -k – 1>
Since PM ⊥ AB ,
∴ 2(2k – 6) + 3 (3k – 1) + (-1)(-k – 1) = 0
⇒4k – 12 + 9k – 3 + k + 1 = 0
⇒14k – 14 = 0
⇒ k = 1

Foot of perpendicular M is
(-1+2, 3+3, 1,-1) i.e (1,6,0)
(ii) Length of Perpendicular
= \(\sqrt{(5-1)^{2}+(4-6)^{2}+(2-0)^{2}}\)
= \(\sqrt{16+4+4}=\sqrt{24}=2 \sqrt{6}\) units

(iii) Let P’ (α, β, γ) be the image of P in the given line.
Then M is the mid-points of [PP’].
∴ \(\frac{\alpha+5}{2}=1, \frac{\beta+4}{2}=6, \frac{\gamma+2}{2}=0\)
⇒ α+5 = 2, β + 4=12, γ+2 = 0
⇒ α = -3,β = 8,γ=-2.
Hence, the reqd. image is (-3,8, -2).

Question 8.
Find the distance between the lines L₁ and L₂ given by:
\(\vec{r}=\hat{i}+2 \hat{j}-4 \hat{k}+\lambda(2 \hat{i}+3 \hat{j}+6 \hat{k})\) and
\(\vec{r}=3 \hat{i}+3 \hat{j}-5 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+6 \hat{k})\) (N.C.E.R.T.)
Solution:
Clearly, L₁ and L₂ are parallel.
Comparing given equations with:
\(\vec{r}=\vec{a}_{1}+\lambda \vec{b}\) and \(\vec{r}=\vec{a}_{2}+\mu \vec{b}\), we have:
\(\vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k}\), so that
\(|\vec{b}|=\sqrt{4+9+36}=\sqrt{49}=7\)

∴ d, the distance between the given lines is given by:

Question 9.
Find the vector equation of the plane that contains the lines \(\vec{r}=(\hat{i}+\hat{j})+\lambda(\hat{i}+2 \hat{j}-\hat{k})\) and the points (-1, 3, -4). Also find the length of the perpendicular from the point (2,1,4) to the plane, thus obtained. (Delhi 2019)
Solution:
Let required plane be
a(x+ l) + b(y-3) + c(z + 4) = 0 …(1)

Plane contains the given line, so it will also con-tain the point (1,1,0).
So, 2a – 2b + 4c = 0
or a-b + 2c = 0
Also, a + 2b – c = 0
From (2) and (3),
\(\frac{a}{-3}=\frac{b}{3}=\frac{c}{3}\) …………(4)

From (1) and (4), required plane is
-3(x + l) + 3(y-3) + 3(z + 4) = 0
⇒ -x-l+;y-3 + z + 4 = 0
⇒ -x + y + z = 0.
Its vector equation is :
\(\vec{r} \cdot(-\hat{i}+\hat{j}+\hat{k})\) = 0.
Length of perpendicular from
\((2,1,4)=\frac{|-2+1+4|}{\sqrt{(-1)^{2}+1^{2}+1^{2}}}=\sqrt{3}\)

Question 10.
Find the vector equation of the plane which contains the line of intersection of the planes:
\(\vec{r} \cdot(\hat{i}+{2} \hat{j}+{3} \hat{k})\) – 4 = 0,
\(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) + 5 = 0
and which is perpendicular to the plane \(\vec{r} \cdot(5 \hat{i}+3 \hat{j}-6 \hat{k})\) + 8 = 0
(Outside Delhi 2019)
Solution:
Required equation of the plane is :

This is perpendicular to the plane
\(\vec{r}\) (5 \(\hat{i}\) + 3 \(\hat{j}\) — 6\(\hat{k}\)) + 8 = 0
⇒ (1+2λ) (5) + (2 + λ) (3) + (3 – λ.) (-6)=0
⇒ 5 + 10λ + 6 + 3λ – 18 + 6λ = 0 ⇒ 191 = 7
⇒19λ = 7
⇒λ = \(\frac { 7 }{ 19 }\)
Puttiong in (1),

Question 11.
Show that die line of intersection of the planes: x + 2y + 3z = 8 and 2x + 3y + 4z = 11 is coplanar with the line:
\(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z+1}{3}\)
Also, find the equation of die plane containing them. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given line is \(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z+1}{2}\) ………. (1)
This is coplanar with the line determined by the planes:
x + 2y + 3z – 8 = 0 …(2)
and 2x + 3y + 4z – 11 =0 …(3)
Here, we show that there exists a plane, which passes through the intersection of (2) and (3) and contains line (1).
Now equation of the plane through the intersection of (2) and (3) is:
(x+2y + 3z-8) + 1(2x+3y+ 4z-11) = 0 …(4)
This passes through 1, -1),
∴ (-1 -2-3-8) + k(-2-3-4-11) = 0
∴ -14-20k = 4
k = \(-\frac { 7 }{ 10 }\)
Putting in (4),
(x + 2y + 3z-8) – \(\frac { 7 }{ 10 }\)(2x + 3y + 4z – 11) = 0
=» (10x + 20y + 30z – 80)
-7 (2x + 3y + 4z – 11) = 0
⇒ 4x + y – 2z + 3 = 0 …(5)
If < a₁ , b₁ , c₁ > are direction-ratios of line (1)
and < a₂, b₂, c₂ > are direction-ratios of normal to plane (5), then
a₁a₂+ b₁b₂+ c₁ c₂ = (1) (4) + 2 (1) + 3 (-2) = 0,
which implies that line (1) lies in plane (5). Hence, the two lines are coplanar and the equation of the plane containing them is 4x + y-2z + 3=0.

Question 12.
Find the vector equation of the line passing through the point (2,3, -1) and parallel to the planes:
\(\vec{r} \cdot(3 \hat{i}+4 \hat{j}+2 \hat{k})\) = 5 andr \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}-2 \hat{k})\) = 4.
Solution:
The given planes are:
\(\vec{r} \cdot(3 \hat{i}+4 \hat{j}+2 \hat{k})\) = 5 and \(\vec{r} \cdot(3 \hat{i}-2 \hat{j}-2 \hat{k})\) = 4
i.e. 3x + 4y + 2z = 5 and 3x- 2y – 2z = 4
⇒3x + 4y + 2z-5 = 0 ……(1)
and 3x – 2y – 2z – 4 = 0 …………. (2)
Let the line through (2,3, -1) be:
\(\frac{x-2}{a}=\frac{y-3}{b}=\frac{z+1}{c}\) …………. (3)

Since (3) is parallel to (1),
∴ a(3) + h(4) + c(2) = 0 -(3)
i.e. 3a + 4b + 2c = 0
Since (3) is parallel to (2), …(4)
∴ (a) (3) + b (-2) + c (-2) = 0 …(5)
⇒ 3a -2b -2c = 0

Question 13.
Find the equation of a plane passing through the points A (2,1,2) and B(4, – 2,1) and per-pendicular to plane \(\vec{r} \cdot(\hat{i}-2 \hat{k})\) = 5. Also, find
the coordinates of the point, where the line pass-ing through the points (3,4,1) and (5,1, 6) crosses the plane thus obtained.
Solution:
Let P(x, y, z) be any point on the plane, which
passes through A(2,1,2) and B(4, -2,1).
∴ \(\overrightarrow{\mathrm{AP}}\) and \(\overrightarrow{\mathrm{AB}}\) lie on the required plane.
Also, the required plane is perpendicular to the
given plane \(\vec{r} \cdot(\hat{i}-2 \hat{k})\) = 5.
∴ Normal to the given plane \(\overrightarrow{n_{1}}=(\hat{i}-2 \hat{k})\) lies on the required plane
⇒ \(\overrightarrow{\mathrm{AP}}\), \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{n_{1}}\) are coplanar,
where \(\overrightarrow{\mathrm{AP}}\) = (x-2) \(\hat{i}\) +(y-1)\(\hat{j}\) + (z-2)\(\hat{k}\)
and \(\overrightarrow{\mathrm{AB}}\) = 2\(\hat{i}\) – 3\(\hat{j}\) – \(\hat{k}\)

⇒ (x-2)(6-0)-(y-1)(-4 + 1) + (z-2)(0 + 3) =0
⇒ 6x – 12 + 3y -3 + 3z – 6 =0
⇒ 2x + y + z = 7 …(1)
Line passing through L(3,4,l) and M(5,1,6) is:

General point on the line is Q(2λ,+ 3, -3λ,+4, 5λ.+1).
Since the line (2) crosses plane (1),
∴ the points Q should satisfy (1).
2(2λ+3) + (-3λ+4) + (5λ,+1) = 7
⇒ 4λ + 6 – 3λ,+4 + 5λ,+ l =7
⇒ 6λ = -4
λ = \(-\frac{2}{3}\)
Hence, the point Q is (\(-\frac{4}{3}\)+3, 2+4, \(-\frac{10}{3}\)+1)
i.e, (\(-\frac{5}{3}\), 6, \(-\frac{7}{3}[latex])

Question 14.
Find the co-ordinates of the point P, where the line through A(3, -4,-5) and B (2, – 3, 1) crosses the plane passing through three points L(2,2,1), M(3,0,1) and N(4, -1,0). Also, find the ratio in which P divides the line segment AB. {C.B.S.E. 2016)
Solution:
Any plane through L(2,2,1) is:
a(x-2) + b(y-2) + c(z-1) = 0 …(1)
Since (1) passes through M(3,0,1),
∴ a(3-2) + b(0-2) + c(1 – 1) = 0
⇒ a-2b + 0 .c = 0 …(2)
Since (1) passes through N (4, – 1,0),
∴ a(4 – 2) + b(- 1 – 2) -(- c(0 – 1) – 0
⇒ 2a – 3b – c = 0 …(3)
Solving (2) and (3),
[latex]\frac{a}{2+0}=\frac{b}{0+1}=\frac{c}{-3+4}=k \text { (say) }\)
⇒ a = 2k,b = k,c = k.
Putting in (1),
2k(x-2) + k(y-2) + k(z- 1) = 0 ⇒ 2(x-2) + (y-2) + (z-l) = O[\-fc*0]
⇒ 2x + y + z-l = 0 …(4)
Now equations of AB are:

and z = -5 + 6r.
Any point on AB is
P(-r+3, r-4,6r-5) …(5)
This lies on plane (4).
∴ 2(-r + 3) + (r-4) + (6r-5)-7 = 0
⇒ 5r = 10
⇒ r= 2.
Putting in (5), the co-ordinates of P are (1,-2,7).
Let P divide the segment [AB] in the ratio of k: 1.

Comparing \(\frac{3+2 k}{k+1}\) = 1
3 + 2k = k + 1
k = -2
Hence, P divides the line segment [AB] in the ratio 2:1 externally.

Question 15.
Find the distance of the point (-1,-5, -10) from the point of intersection of the line \(\vec{r} =2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+\mathbf{1 2} \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})\) = 5. (C.B.S.E. 2018)
Solution:
The given lines is :
\(\vec{r}=2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+12 \hat{k})\)
i.e , \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}\) ……….(1)
and the given plane is r • (J — j + k) = 5
i.e. x – y + z = 5 …(2)
Any point on (1) is (2 + 3k, – 1 + 5k, 2 + 12k)
This lies on (2) if
2 + 3k + 1 – 4k + 2+12k) = 5
⇒ 11k = 0
⇒ k = 0.
Putting in (3), the point of intersection is (2,-1,2).
Its distance from (-1, -5, -10)
= \(\sqrt{(-1-2)^{2}+(-5+1)^{2}+(-10-2)^{2}}\)
= \(\sqrt{9+16+144}=\sqrt{169}\) = 13 units.

Question 16.
Find the vector equation of a line passing through the point (2,3,2) and parallel to the line:
\(\vec{r}=(-2 \hat{i}+3 \hat{j})+\lambda(\hat{2} \hat{i}-3 \hat{j}+6 \hat{k})\)
Also, find the distance between these two lines. Sol. The given line is
r = (-2i + 3j) + X{2i -3j + 6k) …(1)
The required line is :
\(\vec{r}=(2 \hat{i}+3 \hat{j}+2 \hat{k})+\mu(2 \hat{i}-3 \hat{j}+6 \hat{k})\) …(2)
Now, \(\overrightarrow{a_{1}}=-2 \hat{i}+3 \hat{j}\) , \(\overrightarrow{a_{2}}=2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(\vec{b}=2 \hat{i}-3 \hat{j}+6 \hat{k}\)
\(\vec{b}=2 \hat{i}-3 \hat{j}+6 \hat{k}\)
\(\overrightarrow{a_{2}}-\overrightarrow{a_{1}}=4 \hat{i}+2 \hat{k}\)
Reqd. distance,

Question 17.
Find the co-ordinates of the foot of the perpendicular Q drawn from P(3,2,1) to the plane 2x – y + z + 1 = 0. Also,find the distance PQ and the image of the point P treating this plane as a mirror.
Solution:
(i) Equation of PQ is \(\frac{x-3}{2}=\frac{y-2}{-1}=\frac{z-1}{1}=\lambda\)

∴ Co-ordinates of Q are (2λ + 3, – λ + 2, λ + 1).
Since Q lies on the plane 2x-y + z+ 1=0,
4λ + 6 + λ – 2 + λ + 1 + 1 = 0
⇒ 6λ + 6 = 0
⇒ λ = – 1.
∴ Co-ordinates of Q are (- 2 + 3,1 + 2, -1 + 1)
i.e.,{ 1,3,0).

(ii) PQ = \(\sqrt{(1-3)^{2}+(3-2)^{2}+(0-1)^{2}}\)
= \(\sqrt{4+1+1}=\sqrt{6}\) units

(iii) Let P'(x’, y’, z’) be the image
∴ \(\frac{x^{\prime}+3}{2}=1, \frac{y^{\prime}+2}{2}=3, \frac{z^{\prime}+1}{2}=0\)
= x’ = -1, y’ = 4, z’ = -1.
Hence, the image of the point P is (- 1,4, – 1).

Question 18.
Find the vector equation of the plane determined by the points A(3, -1, 2), B(5, 2, 4) and C(-l, -1, 6). Hence, find the distance of the plane, thus obtained, from the origin.
Solution:
The equation of the plane is

⇒ (x-3) (12 – 0) – (y+1) (8 + 8) + (z-2) (0+12) = 0
⇒ 12(x-3)-16(y+1) +12(z-2) = 0
⇒ 3(x-3)-4(y + 1) + 3(z-2) = 0
⇒ 3x – 4y + 3z = 19.
Its vector equation is r \(\vec{r} \cdot(3 \hat{i}-4 \hat{j}+3 \hat{k})\) = 19. Distance of the plane from the origin
= \(\frac{|0-19|}{\sqrt{9+16+9}}=\frac{19}{\sqrt{34}}=\frac{19 \sqrt{34}}{34}\) = units.

Question 19.
Find the co-ordinates of the point where the line \(\frac{x-8}{4}=\frac{y-1}{1}=\frac{z-3}{8}\) intersects the plane 2x + 2y + z=3. Also, find the angle between the line and the plane.
Solution:
(i) The given line is \(\frac{x-8}{4}=\frac{y-1}{1}=\frac{z-3}{8}\)…(1)
and the given plane is2x + 2y + z- 3 = 0 …(2)
Any point on line (1) is (8 + 4-k, l + k, 3 + 8k) …(3)
This lies on plane (2).
∴ 2(8 + 4k) + 2(1 + k) + (3 + 8k) -3 = 0
16 + 8k + 2 + 2k +3 + 8 k – 3 = 0
⇒ 18k + 18 = 0 ⇒ k =-1.
Putting in (3), (4, 0, – 5), which are the required co-ordinates of the point.

(ii) If the line (1) makes an angle ‘θ’ with the plane (2), then the line (1) will make an angle of (90° – θ) with the normal to the plane (2).
Now, direction-ratios of the line (1) are <4,1, 8> and direction-ratios of the normal to the plane (2) are < 2,2,1 >.

Question 20.
Find x such that the four points:
A(5,x, 4), B(4,4,6), C(5,4, -3) and D(7,7, -2) are coplanar.
Solution:
Here,
\(\overrightarrow{\mathrm{AB}}\) = (4\(\hat{i}\) +4\(\hat{j}\) + 6\(\hat{k}\)) – (5\(\hat{i}\) +x\(\hat{j}\) + 4\(\hat{k}\))
= –\(\hat{i}\) +(4-x)\(\hat{j}\) + 2\(\hat{k}\) ,
\(\overrightarrow{\mathrm{BC}}\) = (5\(\hat{i}\) + 4\(\hat{j}\) – 3\(\hat{i}\))-(4\(\hat{i}\) + 4\(\hat{j}\) + 6\(\hat{k}\))
= \(\hat{i}\) – 9\(\hat{k}\)
and \(\overrightarrow{\mathrm{CD}}\) = (7\(\hat{i}\) + 7\(\hat{j}\) -2\(\hat{k}\))-(5\(\hat{i}\) + 4\(\hat{j}\) – 3\(\hat{k}\))
= 2\(\hat{i}\) + 3\(\hat{k}\) + \(\hat{k}\).
The four points are collinear if

⇒ (-1)(0 + 27)-(4-x)(l + 18) + 2(3-0) = 0
⇒ -27-76 + 19x +6=0
⇒ 19x=97.
Hence, x = \(\frac { 97 }{ 19 }\)

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 10 Vectors. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 10 Important Extra Questions Vectors

Vectors Important Extra Questions Very Short Answer Type

Question 1.
Classify the following measures as scalar and vector quantities:
(i) 40°
(ii) 50 watt
(iii) 10gm/cm³
(iv) 20 m/sec towards north
(v) 5 seconds. (N.C.E.R.T.)
Solution:
(i) Angle-scalar
(ii) Power-scalar
(iii) Density-scalar
(iv) Velocity-vector
(v) Time-scalar.

Question 2.
In the figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial. (N.C.E.R.T.)

Solution:
(i) \(\vec{a}, \vec{c}\) and \(\vec{a}\) are collinear vectors.
(ii) \(\vec{a}\) and \(\vec{c}\) are equal vectors.
(iii) \(\vec{b}\), \(\vec{c}\) and \(\vec{d}\) are co-initial vectors.

Question 3.
Find the sum of the vectors:
\(\vec{a}\) = \(\hat{i}-2 \hat{j}+\hat{k}\), \(\vec{a}\) = \(-2 \hat{i}+4 \vec{j}+5 \hat{k}\) and \(\vec{c}\) = \(\hat{i}-6 \hat{j}-7 \hat{k}\). (C.B.S.E. 2012)
Solution:
Sum of the vectors = \(\hat{a}+\hat{b}+\hat{c}\)

Question 4.
Find the vector joining the points P (2,3,0) and Q (-1, – 2, – 4) directed from P to Q. (N.C.E.R.T.)
Solution:
Since the vector is directed from P to Q,
∴ P is the initial point and Q is the terminal point.
∴ Reqd. vector = \(\overrightarrow{\mathrm{PQ}}\)

Question 5.
If \(\vec{a}=x \hat{i}+2 \hat{j}-z \hat{k}\) and \(\vec{b}=3 \hat{i}-y \hat{j}+\hat{k}\) are two equal vectors, then write the value of x + y + z. (C.B.S.E. 2013)
Solution:
Here
\(\vec{a}=\vec{b} \Rightarrow x \hat{i}+2 \hat{j}-z \hat{k}=3 \hat{i}-y \hat{j}+\hat{k}\)
Comparing,A: = 3,2 = -y i.e.y = -2,~z= 1 i.e. z = -1.
Hence, x + y + z = 3 – 2 – 1 = 0.

Question 6.
Find the unit vector in the direction of the sum of the vectors:
\(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}\) and \(\vec{b}=-\hat{i}+\hat{j}+3 \hat{k}\) (N.C.E.R.T.)
Solution:

Question 7.
Find the value of ‘p’ for which the vectors : \(3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel. (A.I.C.B.S.E. 2014)
Solution:
The given vectors \(3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\hat{i}-2 p \hat{j}+3 \hat{k}\) are parallel
If \(\frac{3}{1}=\frac{2}{-2 p}=\frac{9}{3}\) if 3 = \(\frac{1}{-p}\) = 3
if p = \(-\frac{1}{3}\)

Question 8.
If \(\vec{a}\) and \(\vec{b}\) are perpendicular vectors, \(|\vec{a}+\vec{b}|\) = 13 and \(|\vec{a}|\) =5, find the value of \(|\vec{b}|\) (A.I.C.B.S.E. 2014)
Solution:

[∵ \(\vec{a}\) and \(\vec{b}\) are perpendicular ⇒ \(\vec{a}\) \(\vec{b}\) = 0 ]

⇒ \(|\vec{b}|^{2}\) = 169 – 25 = 144.
Hence, \(|\vec{b}|\) = 12.

Question 9.
Find the magnitude of each of the two vectors \(\vec{a}\) and \(\vec{b}\) , having the same magnitude such that the angle between them is 60° and their scalar product is \(\frac { 9 }{ 2 }\) (C.B.S.E. 2018)
Solution:
By the question, \(|\vec{a}|=|\vec{b}|\) …(1)
Now \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\) cos θ
⇒ \(\frac { 9 }{ 2 }\) = \(|\vec{a}||\vec{a}|\) cos 60° [Using (1)]
⇒ \(\frac{9}{2}=|\vec{a}|^{2}\left(\frac{1}{2}\right)\)
⇒ \(|\vec{a}|^{2}\) = 9.
Hence, \(|\vec{a}|=|\vec{b}|\) = 3.

Question 10.
Find the area of the parallelogram whose diagonals are represented by the vectors: \(\vec{a}=2 \hat{i}-3 \hat{j}+4 \hat{k}\) and \(\vec{b}=2 \hat{i}-\hat{j}+2 \hat{k}\) (C.B.S.E. Sample Paper 2018-19)
Solution:

= \(\hat{i}\)(-6 + 4) – \(\hat{j}\)(4 – 8) + \(\hat{k}\)( – 2 + 6)
= – 2\(\hat{i}\) + 4\(\hat{j}\) + 4\(\hat{k}\).
∴ \(|\vec{a} \times \vec{b}|=\sqrt{4+16+16}=\sqrt{36}\)= 6.
∴ Area of the parallelogram = \(\frac{1}{2}|\vec{a} \times \vec{b}|\)
= \(\frac{1}{2}\) (6) = 3 sq. units.

Question 11.
Find the angle between the vectors: \(\vec{a}=\hat{i}+\hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
We have:\(\vec{a}=\hat{i}+\hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-\hat{j}+\hat{k}\)
If ‘θ’ be the angle between \(\vec{a}\) and \(\vec{b}\)

Question 12.
Find \(\vec{a} \cdot(\vec{b} \times \vec{c})\), if : \(\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}\), and \(\vec{c}=3 \hat{i}+\hat{j}+2 \hat{k}\) (A.I.C.B.S.E. 2014)
Solution:
We have:

= 2 (4 – 1) – (1) (-2 – 3) + 3 (-1 – 6)
= 6 + 5-21 = 11 – 21 = -10.

Vectors Important Extra Questions Short Answer Type

Question 1.
If θ is the angle between two vectors:
\(\hat{i}-2 \hat{j}+3 \hat{k}\) and \(3 \hat{i}-2 \hat{j}+\hat{k}\) ,find sinθ.   (C.B.S.E. 2018)
Solution:

Question 2.
X and Y are two points with position vectors \(\overrightarrow{3 a}+\vec{b}\) and \(\vec{a}-3 \vec{b}\) respectively. Write the po-sition vector of a point Z which divides the line segment XY in the ratio 2:1 externally. (C.B.S.E. Outside Delhi 2019)
Solution:
Position vector of
A = \(\frac{2(\vec{a}-3 \vec{b})-(3 \vec{a}+\vec{b})}{2-1}\) = \(-\vec{a}-7 \vec{b}\)

Question 3.
Find the unit vector perpendicular to both \(\overrightarrow{a}\) and \(\overrightarrow{b}\), where:
\(\vec{a}=4 \hat{i}-\hat{j}+8 \hat{k}\) and \(\vec{b}=-\hat{j}+\hat{k}\)
(C.B.S.E. 2019 C)
Solution:

Hence, the unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\)

Question 4.
If \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) , \(\vec{b}=-\hat{i}+{2} \hat{j}+\hat{k}\) and \(\vec{c}=3 \hat{i}+\hat{j}\) are such that \(\vec{a}+\lambda \vec{b}\) is perpendicular to \(\vec{c}\), then find the value of λ . (C.B.S.E. 2019 C)
Solution:
We have:
a = \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) and \(\vec{b}=-\hat{i}+{2} \hat{j}+\hat{k}\)
∴ \(\vec{a}+\lambda \vec{b}=(2 \hat{i}+2 \hat{j}+3 \hat{k})+\lambda(-\hat{i}+2 \hat{j}+\hat{k})\)
= (2 – λ)\(\hat{i}\)+(2 + 2λ)\(\hat{j}\) + (3+λ)\(\hat{k}\).
Now, (\(\vec{a}+\lambda \vec{b}\)) is perpendicular to c ,
∴ \((\vec{a}+\lambda \vec{b}) \cdot \vec{c}=0\)
⇒ ((2 – λ) \(\hat{i}\) + (2 + 2λ)\(\hat{j}\) + (3 + λ\(\hat{k}\)). (3\(\hat{i}\) + \(\hat{j}\)) = 0
⇒ (2 – λ)(3) + (2 + 2λ) (1) + (3 + λ)(0) = 0
⇒ 6 – 3λ + 2 + 2λ = 0
⇒ -λ, + 8 =0.
Hence, λ,=8.

Question 5.
Let \(\vec{a}=\hat{i}+2 \hat{j}-3 \hat{k}\) and \(\vec{b}=3 \hat{i}-\hat{j}+2 \hat{k}\) be two vectors. Show that the vectors (\(\vec{a}+\vec{b}\)) and
(\(\vec{a}-\vec{b}\)) are perpendicular to each other. (C.B.S.E. Outside Delhi 2019)
Solution:
Here, \(\vec{a}+\vec{b}\) = (\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\)) + (3\(\hat{i}\) – \(\hat{j}\) + 2\(\hat{k}\))
= 4\(\hat{i}\) + \(\hat{j}\) –\(\hat{k}\)
and \(\vec{a}-\vec{b}\) = (\(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\)) – (3\(\hat{i}\) – j + 2k)
= -2\(\hat{i}\) + 3\(\hat{j}\) – 5\(\hat{k}\).
Now
\(\vec{a}+\vec{b}\) . \(\vec{a}-\vec{b}\) = (4\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\))- (-2\(\hat{i}\) + 3 \(\hat{j}\) – 5\(\hat{k}\))
= (4) (- 2) + (1) (3)+(-1) (- 5)
= – 8 + 3 + 5 = 0.
Hence \(\vec{a}+\vec{b}\) is perpendicular to \(\vec{a}-\vec{b}\).

Question 6.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference
is √3 . (C.B.S.E. 2019)
Solution:

By the question,
\(|\overrightarrow{\mathrm{AB}}|=|\overrightarrow{\mathbf{B C}}|=|\overrightarrow{\mathrm{AC}}|=1\)
⇒ ΔABC is equilateral, each of its angles be¬ing 60°
⇒ ∠DAB = 2 x 60° = 120° and ∠ADB = 30°.
By Sine Formula,
\(\frac{\mathrm{DB}}{\sin \angle \mathrm{DAB}}=\frac{\mathrm{AB}}{\sin \angle \mathrm{ADB}}\)

Question 7.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|\) = 3, \(|\vec{b}|\) = 5 and \(|\vec{a}|\) = 7, then find the value of \(\overrightarrow{a} \cdot \overrightarrow{b}+\overrightarrow{b} \cdot \overrightarrow{c}+\overrightarrow{c} \cdot \overrightarrow{a}\)
(C.B.S.E. Sample Paper 2019-20)
Solution:

Question 8.
Find \(|\vec{a}-\vec{b}|\), if two vectors a and b are such that \(|\vec{a}|\) = 2,\(|\vec{b}|\) = 3 and \(\vec{a} \cdot \vec{b}\) = 4. (N.C.E.R.T.)
Solution:

Question 9.
Find the work done by the force \(\overrightarrow{\mathbf{F}}=2 \hat{i}+\hat{j}+\hat{k}\) acting on a particle, if the particle is displaced from the point with position vector \(2 \hat{i}+\hat{j}+2 \hat{k}\) to the point with position vector \(3 \hat{i}+4 \hat{j}+5 \hat{k}\)
Solution:
Here F = 2 \(\hat{i} \)+ \(\hat{j} \) + \(\hat{k} \)
and d = (3 \(\hat{i} \) + 4\(\hat{j} \) + 5k) – (2 \(\hat{i} \) + 2\(\hat{j} \) + 2\(\hat{k} \) )
– \(\hat{i} \) +2\(\hat{j} \) + 3\(\hat{k} \) .
∴ Work done = \(\overrightarrow{\mathrm{F}} \cdot \vec{d}\)
= (2 \(\hat{i} \) + \(\hat{j} \) + \(\hat{k} \) ). ( \(\hat{i} \) + 2\(\hat{j} \) + 3\(\hat{k} \) )
= (2) (1) + (1) (2) + (1) (3)
= 2 + 2 + 3
= 7 units.

Question 10.
Find ‘λ’ if
(2\(\hat{i} \) + 6\(\hat{j} \) + 14\(\hat{k} \)) x (\(\hat{i} \) – λ\(\hat{j} \) + 7\(\hat{k} \)) = 0. (A.I.C.B.S.E. 2010)
Solution:
We have:
(2\(\hat{i}\) + 6\(\hat{j}\) + 14\(\hat{k}\)) x (\(\hat{i}\) – λ\(\hat{j}\) + 7\(\hat{k} \)) = 0
⇒ \(\hat{i} \) (42 + 14λ) – \(\hat{j}\)(14-14) + \(\hat{k}\) (-2λ – 6) = 0
⇒ 14\(\hat{i} \)(λ + 3)-2(λ + 3) ifc = o
= λ+3 = 0.
Hence, λ = -3.

Question 11.
If \(\vec{a}\) and \(\vec{b}\) are two vectors such that \(|\vec{a} \cdot \vec{b}|\)
=\(|\vec{a} \times \vec{b}|\), then what is the angle between \(\vec{a}\) and b ? (A.I.C.B.S.E. 2010)
Solution:
We have \(|\vec{a} \cdot \vec{b}|=|\vec{a} \times \vec{b}|\)
⇒ \(|\vec{a}||\vec{b}| \cos \theta=|\vec{a}||\vec{b}| \sin \theta\)
⇒ cos θ = sin θ ⇒ tan θ = 1 ⇒ θ = 45°.
Hence, the angle between \(\vec{a}\) and \(\vec{a}\) = 45°.

Question 12.
If \(\vec{a}=2 \hat{i}+3 \hat{j}+\hat{k}\), b = \(\vec{b}=\hat{i}-2 \hat{j}+\hat{k}\) and \(\vec{c}=-3 \hat{i}+\hat{j}+2 \hat{k}\) ,find \([\vec{a} \vec{b} \vec{c}]\).   (C.B.S.E. 2019)
Solution:
We have : \(\vec{a}\) = 2\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\), \(\vec{b}\) = \(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\) and \(\vec{c}\) = – 3\(\hat{i}\) + \(\hat{j}\) + 2\(\hat{k}\)
∴ \([\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{rrr}
2 & 3 & 1 \\
1 & -2 & 1 \\
-3 & 1 & 2
\end{array}\right|\)
= 2 (-4-1)-3(2 + 3)+ 1.(1 -6)
= 2(-5)-3(5)+ 1(-5)
= -10-15-5 = -30.

Question 13.
For three non-zero vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\), prove that \([\vec{a}-\vec{b}, \vec{b}-\vec{c}, \vec{c}-\vec{a}]\) = 0. (C.B.S.E. 2019)
Solution:

Vectors Important Extra Questions Long Answer Type

Question 1.
Let \(\vec{a}=4 \hat{i}+5 \hat{j}-\hat{k}\) and \(\vec{b}=\hat{i}-4 \hat{j}+5 \hat{k}\) and \(\vec{c}=3 \hat{i}+\hat{j}-\hat{k}\). Find a vector \(\vec{a}\) which is perpendicular to both \(\vec{c}\) and \(\vec{b}\) and
\(\vec{d} \cdot \vec{a}\) =21. (C.B.S.E. 2018)
Solution:
Wehave: \(\vec{a}\) = 4\(\hat{i}\) + 5\(\hat{j}\) – \(\hat{k}\)
\(\vec{b}\) = \(\hat{i}\) – 4\(\hat{j}\) + 5\(\hat{k}\) and
\(\vec{c}\) = 3\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\)
Let \(\vec{d}\) = x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)

since \(\vec{d}\) is perpendicular to both \(\vec{c}\) and \(\vec{b}\)
\(\vec{d} \cdot \vec{c}\) = 0 and \(\vec{d} \cdot \vec{b}\) = 0
⇒ (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)) . (3\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\)) = 0

and (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)) . (\(\hat{i}\) -4\(\hat{j}\)+5\(\hat{j}\)) = 0
⇒ 3x + y-z = 0 …(1)
and x-4y + 5z = 0 …(2)
Also, \(\vec{d} \cdot \vec{a}\) = 21
⇒ (x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)). (4\(\hat{i}\) + 5\(\hat{j}\) – \(\hat{k}\)) =21
⇒ 4x + 5y-z = 21 …(3)
Multiplying (1) by 5,
1 5x + 5y – 5z = 0 …(4)
Adding (2) and (4),
16x + y = 0 …(5)
Subtracting (1) from (3),
x + 4y = 21 …(6)
From (5),
y = -16x …(7)
Putting in (6),
x – 64x = 21
-63x: = 21
Putting in (7), y = \(-16\left(-\frac{1}{3}\right)=\frac{16}{3}\)
Putting in (1), \(3\left(-\frac{1}{3}\right)+\frac{16}{3}\) – z = 0
z = 13/3
Hence \(\vec{d}=-\frac{1}{3} \hat{i}+\frac{16}{3} \hat{j}+\frac{13}{3} \hat{k}\)

Question 2.
If \(\vec{p}=\hat{i}+\hat{j}+\hat{k}\) and \(\vec{q}=\hat{i}-2 \hat{j}+\hat{k}\) ,find a vector of magnitude 5√3 units perpendicular to the vector \(\vec{q}\). and coplanar with vector \(\vec{p}\) and \(\vec{q}\). (C.B.S.E. 2018)
Solution:
Let \(\vec{r}=a \hat{i}+b \hat{j}+c \hat{k}\) be the vector.
Since \(\vec{r} \perp \vec{q}\)
(1) (a) + (-2) (b) + 1 (c) = 0
⇒ a – 2b + c = 0
Again, \(\vec{p}\) , \(\vec{q}\) and \(\vec{r}\) and coplanar,

⇒ (1) (-2c – b) – (1) (c – a) + (1) (b + 2a) = 0
⇒ -2c-b-c + a + b + 2a = 0
⇒ 3a – 3c = 0
⇒ a – c – 0
Solving (1) and (2),

Question 3.
If \(\hat{i}+\hat{j}+\hat{k}, \quad 2 \hat{i}+5 \hat{j}, \quad 3 \hat{i}+2 \hat{j}-3 \hat{k}\) and \(\hat{i}-6 \hat{j}-\hat{k}\) respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find
whether \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{CD}}\) arecollinearornot
(C.B.S.E. 2019)
Solution:
Note : If ‘θ’ is the angle between AB and CD,
then θ is also the angle between \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C D}}\) .
Now \(\overrightarrow{\mathbf{A B}}\) = Position vector of B – Position vector of A

Since 0 ≤ θ ≤ π, it follows that θ = π. This shows that \(\overrightarrow{\mathbf{A B}}\) and \(\overrightarrow{\mathbf{C D}}\) are collinear.
Alternatively, \(\overrightarrow{\mathrm{AB}}=-\frac{1}{2} \overrightarrow{\mathrm{CD}}\) which implies
that \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{CD}}\) are collinear vectors.

Question 4.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) and \(|\vec{a}|\) = 3, \(|\vec{b}|\) = 5, and \(|\vec{c}|\) =7, find the angle between \(\vec{a}\) and \(\vec{b}\) . (C.B.S.E. 2014)
Solution:

where ‘θ’ is the angle between a and b
⇒ (3)² + (5)² + 2 (3) (5) cos θ = (7)²
⇒9 + 25 + 30 cos θ = 49
⇒ 30 cos θ = 49 – 34 ⇒ cos θ = \(\frac{1}{2}\)
⇒ θ = 60°.
Hence, the angle between \(\vec{a}\) and \(\vec{b}\) is 60°.

Question 5.
If \(\vec{a}, \vec{b}, \vec{c}\) are mutually perpendicular vectors of equal magnitude, show that \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b}\) and \(\vec{c}\) . Also, find the angle, which \(\vec{a}+\vec{b}+\vec{c}\) makes with \(\vec{a}\) or \(\vec{b}\) or \(\vec{c}\) . (C.B.S.E. 2017)
Solution:

Let α, β and γ be the angles which \(\vec{a}+\vec{b}+\vec{c}\)
makes with \(\vec{a}, \vec{b}\) and \(\vec{c}\) respectively.

From (1), (3), (4) and (5),
cos α = cos β = cos γ ⇒ α = β = γ
Hence, \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a}, \vec{b}\) and \(\vec{b}\)

Question 6.
If with reference to a right-handed system of mutually perpendicular unit vectors
\(\hat{i}, \hat{j}, \hat{k}, \vec{\alpha}=3 \hat{i}-\hat{\jmath}\) where \(\vec{\beta}=2 \hat{i}+\hat{j}-3 \hat{k}\) then express \(\vec{\beta}\) in the form \(\vec{\beta}=\vec{\beta}_{1}+\vec{\beta}_{2}\) ,
where \(\vec{\beta}_{1}\) is parallel to \(\vec{\alpha}\) and \(\vec{\beta}_{2}\) is perpendicular to \(\vec{\alpha}\) . (N.C.E.R.T.; C.B.S.E. (F) 2013)
Solution:

Comparing co-efficients, 2 = 3λ + a₁
1= – λ + a₂ , – 3 = a3
⇒ a₁= 2 – 3λ, a₂ = 1 + λ,
a₃ = -3 …(4)
Putting in (3), 3 (2-3λ)-(1 + λ) = 0
⇒ – 10λ +5 = 0
= λ = \(\frac { 1 }{ 2 }\)
From (4) a₁ = 2 – 3\(\frac { 1 }{ 2 }\) = 2-\(\frac { 3 }{ 2 }\) = \(\frac { 1 }{ 2 }\)
and a₂ = 1 + \(1+\frac{1}{2}=\frac{3}{2}\)

Question 7.
If \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) find: \((\vec{r} \times \hat{i}) \cdot(\vec{r} \times \hat{j})+x y\) (C.B.S.E 2015)
Solution:

Question 8.
Show that the points A, B, C with position vectors \(2 \hat{i}-\hat{j}+\hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) and \(3 \hat{i}-4 \hat{j}-4 \hat{k}\) respectively, are the vertices of a right angled triangle. Hence, find the area of the triangle. (A.I.C.B.S.E. 2017)
Solution:
Let(2\(\hat{i}\) – \(\hat{i}\) + \(\hat{k}\)), \(\hat{i}\) -3\(\hat{j}\) – 5\(\hat{k}\))
and (3\(\hat{i}\) -4\(\hat{j}\) -4\(\hat{k}\)) be the position vectors of the vertices A, B and C respectively.
.-. AB = (\(\hat{i}\) – 3\(\hat{j}\) – 5\(\hat{k}\)) – (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\))
= – \(\hat{i}\) – 2\(\hat{j}\) – 6\(\hat{k}\)
BC = (3\(\hat{i}\) -4\(\hat{j}\) – 4\(\hat{k}\))-(\(\hat{i}\) -3\(\hat{j}\) – 5\(\hat{k}\))
= 2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)
and = (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)) -(3\(\hat{i}\) – 4\(\hat{j}\) – 4\(\hat{k}\))
= – \(\hat{i}\) + 3 \(\hat{j}\) + 5\(\hat{k}\).
Now, \(\overrightarrow{\mathrm{BC}} \cdot \overrightarrow{\mathrm{CA}}\) = (2\(\hat{i}\) – \(\hat{j}\) + \(\hat{k}\)). ( – \(\hat{i}\) + 3\(\hat{j}\) + 5\(\hat{k}\))
= (2)(-1) + (-1)(3) + (1)(5) = -2 -3 + 5 = 0.
Thus, \(\overrightarrow{\mathrm{BC}} \perp \overrightarrow{\mathrm{CA}}\)
⇒ ∠C = 90°.
Hence, AABC is rt. angled.

And, area of triangle = \(\frac{1}{2}|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|\) ………… (1)
But \(\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
-1 & 3 & 5 \\
-2 & 1 & -1
\end{array}\right|\)
= \(\hat{i}\)(-3-5) – \(\hat{j}\)(1 + 10) + \(\hat{k}\)(-1 + 6)
= -8\(\hat{i}\) – 11\(\hat{i}\) + 5\(\hat{i}\)
∴ \(|\overrightarrow{\mathrm{CA}} \times \overrightarrow{\mathrm{CB}}|=\sqrt{64+121+25}=\sqrt{210}\)
Hence, area of triangle = \(\frac{1}{2} \sqrt{210}\) sq. units

Question 9.
Find the value of ‘λ’ if four points with position vectors \(\mathbf{3} \hat{i}+6 \hat{j}+9 \hat{k}, \hat{i}+2 \hat{j}+3 \hat{k}\), \(2 \hat{i}+3 \hat{j}+\hat{k}\) and \(4 \hat{i}+6 \hat{j}+\lambda \hat{k}\) are coplanar.   (A.I.C.B.S.E. 2017)
Solution:
Let A, B, C and D be the points with position

The four points are coplanar if \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}\) are coplanar

if – 2(λ – 1 +6) + 4(λ – 1 + 4) -6 (3 – 2) = 0
if -2λ.-10 + 4λ + 12 – 6 = 0
if 2λ,- 4 = 0 if λ = 2.
Hence, λ, = 2.

Question 10.
Let \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}\) and \(\vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\). Then :
(a) Let c₁ = 1 and c₂ = 2, find c₃ which makes \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar
(b) Let c₂ = -1 and c₃ = 1, show that no value of c₁ can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar. (C.B.S.E. 2017)
Solution:
We have : \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=\hat{i}\) and
\(\vec{c}=c_{1} \hat{i}+c_{2} \hat{j}+c_{3} \hat{k}\)
(a) Here c₁ = 1 and c₂ = 2.
∴ \(\vec{c}=\hat{i}+2 \hat{j}+c_{3} \hat{k}\)
Since \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar, [Given]
∴ \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
1 & 2 & c_{3}
\end{array}\right|=0\)
⇒ (-1) [c₃ – 2] = 0
⇒ c₃ – 2 = 0
⇒ c₃ = 2.

(b) Here c₂ = -1, c₃ = 1.
∴ \(\vec{c}=c_{1} \hat{i}-\hat{j}+\hat{k}\)
Since \(\vec{a}, \vec{b} \text { and } \vec{c}\) are coplanar, [Given]
∴ \(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
c_{1} & -1 & 1
\end{array}\right|=0\)
⇒ (-1) [1 +1] = 0
⇒ -2 = 0, which is false.
Hence, no value of c₁ can make \(\vec{a}, \vec{b} \text { and } \vec{c}\) coplanar.

Question 11.
Show that the vectors \(\vec{a}, \vec{b} \text { and } \vec{c}\)are coplanar if \(\vec{a}+\vec{b}, \vec{b}+\vec{c}\) and \(\vec{c}+\vec{a}\) are coplanar. (N.C.E.R.T. (Supplement); (C.B.S.E. 2016)
Solution:

Question 12.
Prove that \([\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}, \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}}]=\mathbf{2}\left[\begin{array}{ccc}
\rightarrow & \overrightarrow{\mathbf{b}} & \overrightarrow{\mathbf{c}}
\end{array}\right]\)
(N.C.E.R.T. (Supplement); C.B.S.E. 2014)
Solution:

Question 13.
Show that the four points A, B, C and D with position vectors: \(\hat{i}+2 \hat{j}-\hat{k}, 3 \hat{i}-\hat{j}, 2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(4 \hat{i}+3 \hat{k}\) respectively are coplanar. (C.B.S.E. 2019 C)
Solution:

The four points A, B, C and D are coplanar ⇒ [AB,BC,CD]=O
⇒ \([\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{CD}}]=0\)
⇒ \(\left|\begin{array}{ccc}
2 & -3 & 1 \\
-1 & 4 & 2 \\
2 & -3 & 1
\end{array}\right|=0\)
⇒ 2(4 + 6) + 3 (-1 – 4) + 1.(3 – 8) = 0
⇒ 20 – 15 – 5 = 0
⇒ 0 = 0, which is true.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 9 Differential Equations. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 9 Important Extra Questions Differential Equations

Differential Equations Important Extra Questions Very Short Answer Type

Question 1.
Find the order and the degree of the differential equation: \(x^{2} \frac{d^{2} y}{d x^{2}}=\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{4}\)
(Delhi 2019)
Solution:
Here, order = 2 and degree = 1.

Question 2
Determine the order and the degree of the differential equation:\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (C.B.S.E. 2019 C)
Solution:
Order = 2 and Degree = 1.

Question 3.
Form the differential equation representing the family of curves: y = b (x + a), where « and b are arbitrary constants. (C.B.S.E. 2019 C)
Solution:
Wehave:y= b(x + a) …(1)
Diff. w.r.t. x, b.
Again diff. w.r.t. x, \(\frac{d^{2} y}{d x^{2}}\) = 0,
which is the reqd. differential equation.

Question 4.
Write the general solution of differential equation:
\(\frac{d y}{d x}\) = e^x+y (C.B.S.E. Sample Paper 2019-20)
Solution:
We have: \(\frac{d y}{d x}\) = e^x+y
⇒ e^-y dy = e^x dx [Variables Separable
Integrating, \(\int e^{-y} d y+c=\int e^{x} d x\)
⇒ – e^-y + c = e^x
⇒ e^x + e^-y = c.

Question 5.
Find the integrating factor of the differential equation:
y\(\frac{d y}{d x}\) – 2x = y³e^-y
Solution:
The given equation can be written as.

Question 6.
Form the differential equation representing the family of curves y = a sin (3x – b), where a and b are arbitrary constants. (C.B.S.E. 2019C)
Solution:
We have: y – a sin (3x – b) …(1)
Diff. W.r.t y \(\frac{d y}{d x}\) = a cos (3x – b) .3
= 3a cos (3x – b)
\(\frac{d^{2} y}{d x^{2}}\) = -3a sin (3x – b) 3
= -9a sin (3x – b)
= -9y [Using (1)]
\(\frac{d^{2} y}{d x^{2}}\) + 9y = 0,m
which in the reqd. differential equation.

Differential Equations Important Extra Questions Short Answer Type

Question 1.
Determine the order and the degree of the differential equation:
\(\left(\frac{d y}{d x}\right)^{3}+2 y \frac{d^{2} y}{d x^{2}}=0\) (Outside Delhi 2019C)
Solution:
Order = 2 and Degree = 1.

Question 2.
Form the differential equation representing the family of curves: y = e^2x (a + bx), where ‘a’ and ‘h’ are arbitray constants. (Delhi 2019)
Solution:
We have : y = e^2x (a + bx) …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = e^2x (b) + 2e2x (a + bx)
⇒ \(\frac{d y}{d x}\) = be^2x + 2y ………….. (2)
Again diff. w.r.t. x,
\(\frac{d^{2} y}{d x^{2}}\) = 2be^2x + 2^2x
\(\frac{d^{2} y}{d x^{2}}\) = 2(\(\frac{d y}{d x}\) – 2y) + \(\frac{d y}{d x}\)
[Using (2)]
Hence, \(\frac{d^{2} y}{d x^{2}}\) -4 \(\frac{d y}{d x}\) + 4y = 0, which is the reqd. differential equation.

Question 3.
Solve the following differentia equation:
\(\frac{d y}{d x}\) + y = cos x – sin x (Outside Delhi 2019)
Solution:
The given differential equation is :
\(\frac{d y}{d x}\) + y = cos x – sin x dx Linear Equation
∴ I.F. = e^∫1dx = e^x
The solution is :
y.e^x = ∫ (cos x — sin x) e^x dx + C
⇒ y.e^x = e^x cos x + C
or y = cos x + C e^-x

Question 4.
Solve the following differential equation :
\(\frac{d x}{d y}\) + x = (tan y + sec²y). (Outside Delhi 2019 C)
Solution:
The given differential equation is :
\(\frac{d x}{d y}\) + x = (tany + sec²y).
Linear Equation
∵ I.F. = Jldy = ey
∴ The solution is :
x. ey = ∫ ey (tan y + sec² y)dy + c
⇒ x. ey = ey tan y + c
= x = tan y + c e-y, which is the reqd. solution.

Differential Equations Important Extra Questions Long Answer Type 1

Question 1.
Solve the differential equation
(x² – y²)dx + 2xydy = 0 (C.B.S.E. 2018)
Solution:

log x = -log (1 + v²) + log C
x(1 + v²) = C
x(1 + \(\frac{y^{2}}{x^{2}}\)) = C
x² + y² = C.

Question 2.
Find the particular solution of the differential equation (1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\), given that y = 0 when x = 1(C.B.S.E. 2018 C)
Solution:

Solution is y( 1 + x²) = \(\int \frac{1}{1+x^{2}} d x\)
= tan^-1 x + C
When y = 0,x = 1,
then 0 = \(\frac{\pi}{4}\) + C
C = \(\frac{\pi}{4}\)
∴ y(1 + x²) = tan ^-1 x – \(\frac{\pi}{4}\)
i.e, y = \(\frac{\tan ^{-1} x}{1+x^{2}}-\frac{\pi}{4\left(1+x^{2}\right)}\)

Question 3.
Find the differential equation representing the family of curves y = ae^{bx + 5}, where ‘a’and ‘A’are arbitrary constants. {C.B.S.E. 2018)
Solution:
We have: y = ae^{bx + 5} + 5 …(1)
Diff. w.r.t. x, \(\frac{d y}{d x}\) = ae^{bx + 5}. (b)
\(\frac{d y}{d x}\) = dy ……(2) [Using (1)]]
Again diff. w.r.t x.,
\(\frac{d^{2} y}{d x^{2}}=b \frac{d y}{d x}\) ………(3)

Dividing (3) by (2),

which is the required differential equation.

Question 4.
Find the particular solution of the differential equation x dx – ye^y \(\sqrt{1+x^{2}}\) dy = 0, given that y = 1 when x = 0. (C.B.S.E. 2019 C)
Solution:
The given differential equation is:

When x = 0,y = 1, ∴ 1 = c + c(0) ⇒ c = 1.
Putting in (2), \(\sqrt{1+x^{2}}\) = 1 + e^y(y -1),
which is the reqd. particular solution.

Question 5.
Obtain the differential equation of the family of circles, which touch the x-axis at the origin.   (N.C.E.R.T.; C.B.S.E. Sample Paper 2018)
Solution:
Let (0, α) be the centre of any member of the family of circles.

Then the equation of the family of circles is : x² + (y-α)² = α²
⇒ x² + y² – 2αy = 0 …(1)
Diff. w.r.t. x, 2x + 2y \(\frac{d y}{d x}\) 2α \(\frac{d y}{d x}\) = 0

which is the required differential equation.

Question 6.
Obtain the differential equation representing the family of parabolas having vertex at the origin and axis along the positive direction of x-axis. (N.C.E.R.T.)
Solution:
Let S (a, 0) be the focus of any member of the family of parabolas.
Then the equation of the family of curves is y² = 4 ax …………. (1)
Diff. w.r.t. x, 2y\(\frac{d y}{d x}\) = 4a ……………. (2)
Using (2) in (1), we get:
y² = (2y\(\frac{d y}{d x}\))x

y² – 2xy\(\frac{d y}{d x}\) = 0
which is the required differential equation.

Question 7.
Find the general solution of the differential equation:
(tan²x + 2 tanx + 5) \(\frac{d y}{d x}\) = 2 (1 + tanx) sec² x
Solution:
We have : (tan² x + 2 tan x + 5)\(\frac{d y}{d x}\)
= 2 (1 + tanx) sec²x
Integrating

Put t² + 2t + 5 = z
so that (2t+ 2) dt = dz.
∴ From (2),
1 = \(\int \frac{d z}{z}\) = log| z | = log |t² + 2t + 5|
= log |tan² x| + 2 tan x + 5|
From (1), y = log |tan² x| + 2 tan x + 5| + c,
which is the required general solution.

Question 8.
Solve the differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y(0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :
\(\frac{d y}{2 e^{-y}-1}=\frac{d x}{x+1}\)
| Variables Separable

Integrating, \(\int \frac{e^{y} d y}{2-e^{y}}=\int \frac{d x}{x+1}\)
⇒ – log |2 – e^y| + log |C| = log |x + 1|
⇒ (2 – e^y) (x + 1) = C.
When x = 0, y = 0, then C = 1.
Hence, the solution is (2 – e^y) (x + 1) = 1.

Question 9.
Solve: (a) (i) \(\frac{d y}{d x}\) = 1 + x + y + xy
(ii) xyy’ = 1 + x + y + xy. (N.C.E.R.T.)
(b) Find the particular solution of the differential dy
equation \(\frac{d y}{d x}\) = 1 + x + y + xy, given that y = 0 when x = 1. (A.I.C.B.S.E. 2014)
Solution:
(a), (i) The given equation is :
\(\frac{d y}{d x}\) = 1 + x + y + xy
\(\frac{d y}{d x}\) = (1 +x) (1 +y)
\(\frac{d}{1+y}\) = (1 + x)dx.
|Variables Separable

Integrating,
\(\int \frac{d y}{1+y}\) = ∫(1 + x)dx + c
⇒ log |1 + y | = x + \(\frac { 1 }{ 2 }\) x² + c,
which is the required solution.

(ii) The given equation is xyy’ = 1 + x + y + xy
⇒ xy\(\int \frac{d y}{1+y}\) = (1 + x)(1 + y)

= y – log|1 + y| = log|x|+ x + c
= x + log |x (1 + y)|+ c,
which is the required solution.

(b) From part (a) (i),
Iog|1+y| = x + \(\frac { 1 }{ 2 }\)x² + c …(1)
When x = 1, y = 0, then:
log |1+0|= 1 + \(\frac { 1 }{ 2 }\)(1)² + c
log 1 = 1 + \(\frac { 1 }{ 2 }\) + c
0 = \(\frac { 3 }{ 2 }\) + c
c = \(-\frac { 3 }{ 2 }\)
Putting in (1), log |1 + y| = x + \(\frac { 1 }{ 2 }\)x² – \(\frac { 3 }{ 2 }\)
which is the required particular solution.

Question 10.
Solve the differential equation:
\(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
given thaty = 1 when x = 0. (Outside Delhi 2019)
Solution:
The given equation is \(\frac{d y}{d x}\) = 1 + x² + y² + x²y²
⇒ \(\frac{d y}{d x}\) = (1+x²)(1 +y²)
⇒ \(\frac{d y}{1+y^{2}}\) (x² + 1) dx
|Variables Separable

Integrating, ∫\(\frac{d y}{1+y^{2}}\) = ∫(x² + 1) dx + C
tan^-1y = \(\frac{x^{3}}{3}\) + x + C ………. (1)
Where x = 0,y = 1,
∴ tan^-1 (1) = C
C = \(\frac{\pi}{4}\)
Putting in (1),
tan^-1 y = \(\frac{x^{3}}{3}+x+\frac{\pi}{4}\)
which is the reqd. particular solution.

Question 11.
Find the particular solution of the differential equation: e^x tan y dx + (2 – e^x) sec² y dy = 0, given thaty = \(\frac{\pi}{4}\) where x = 0.
Solution:
The given differential equation is:

∴ From (1),
log C + log |e^x – 2| = log |tan y|
⇒ tany = C(e^x – 2) …(2)
When x = 0, y = y = \(\frac{\pi}{4}\)
∴ 1 = C(1 – 2)
C = -1
Putting in (2),
tan y = 2 – e^x
which is the required particular solution.

Question 12.
Find the particular solution of the following differential equation:
cosy dx + (1 + 2e^-x) siny dy = 0; y(0) = \(\frac{\pi}{4}\) .
(CBSE Sample Paper 2018 – 19)
Solution:
The given differential equation is:
cos y dx + (1 + 2e^-x) sin ydy = 0

log |e^x| – log |cos y| = log|C|
e^x + 2 = C cos y ….. (1)

Substituting, x = 0, y = \(=\frac{\pi}{4}\) in(1),we get:
1 + 2 = C cos \(=\frac{\pi}{4}\)
C = \(\frac{3}{1 / \sqrt{2}}\)
C = 3√2
Putting in (1),
e^x + 2 = 3√2 cos y
which is the required particular solution.

Question 13.
Find the particular solution of the following differential equation:
(x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1 ; y = 0 when x = 0. (C.B.S.E. 2012)
Solution:
The given equation is (x + 1) \(\frac{d y}{d x}\) = 2e^-y – 1

-log|2 – e^y| = log|x + 1| + log|c|,
where c’ = log |c|
⇒ log \(\left|\frac{1}{2-e^{y}}\right|\) = log |c(x + 1)|
⇒ \(\frac{1}{2-e^{y}}\) = c(x + 1)
When x = 0, y = 0;
\(\frac{1}{2-e^{0}}\) = c(0 + 1)
⇒ c = \(\frac{1}{2-1}=\frac{1}{1}\) = 1

Putting (1)
\(\frac{1}{2-e^{y}}\) = 1.(x + 1)
⇒ (x + 1)(2 – e^y) = 1
which is the required particular solution.

Question 14.
Solve the differential equation:
(1 – y²) (1 + log x)dx + 2xy dy = 0, given that when x = 1 ,y = 0.
(C.B.S.E. 2016)
Solution:
The given equation is :
(1 – y²) (1 + log x)dx + 2xy dy = 0

Putting in (1),
\(\frac{(1+\log x)^{2}}{2}\) = log|1 – y²| + 1/2
(1 + log x)² = 2 log|1 – y²| + 1
which is the required solution.

Question 15.
Solve the differential equation:
x cos x (\(\frac { y }{ x }\)) \(\frac{d y}{d x}\) = y cos(\(\frac { y }{ x }\)) = x (C.B.S.E. 2019 C)
Solution:
The given equation is:

Put \(\frac { y }{ x }\) = v i.e, y = vx so that \(\frac { dy }{ dx }\) = v + x \(\frac { dv }{ dx }\)
∴ (1) becomes:
cos v (v + x\(\frac { dv }{ dx }\)) = vcosv + 1
= v + x \(\frac { dv }{ dx }\) = v + \(\frac { 1 }{ cos v }\)
x \(\frac { dv }{ dx }\) = \(\frac { 1 }{ cos v }\)
cos v dv = \(\frac { dx }{ x }\)
[Variables Seperable]

Integrating, ∫ cos v dv = ∫ \(\frac{d x}{ x}\) + c
sin = log|x| + c
sin \(\frac{y}{ x}\) = log|x| + c,
which is the reqd. solution.

Question 16.
Find the general solution of the differential equation: \(\frac{d x}{d y}=\frac{y \tan y-x \tan y-x y}{y \tan y}\) (C.B.S.E. Sample Paper 2018-19)
Solution:
The given differential equation is :

|Linear Equation
Comparing with \(\frac{d x}{d y}\) + Py = Q, we have :
‘P’ = \(\frac{1}{y}+\frac{1}{\tan y}\) and ‘Q’ = 1

∴ I.F = \(e^{\int\left(\frac{1}{y}+\frac{1}{\tan y}\right) d y}=e^{\log y+\log \sin y}\)
e^log(ysiny) = ysiny.
∴ The solution is
x x I.F. = ∫ (Q x I.F.)dy + C
⇒ x(y sin y) = ∫(1 x y sin y)dy + C
⇒ xy sin y = ∫ y sin y dy + C
⇒ xy sin y = y (- cos y) – ∫(1) -cos y)dy + C

(Integrating by Parts)
⇒ xy sin y = – y cos y + ∫ cos ydy + C
⇒ xy sin y = – y cos y + sin y + C
⇒ x = \(\frac{\sin y-y \cos y+C}{y \sin y}\)
which is the required general solution.

Question 17.
Solve the differential equation :
xdy – ydx = \(\sqrt{x^{2}+y^{2}}\) dx , given that y = 0 when x = 1. (C.B.S.E. 2019)
Solution:
The given equation can be written as :


where x = 1, y = 0
∴ 0 + \(\sqrt{1+0} \) = c(1)
⇒ c = 1
Putting in (2), y + \(\sqrt{x^{2}+y^{2}}\) = x²,
which is the reqd. solutions.

Question 18.
Solve the following differential equation:
\(x y \log \left(\frac{y}{x}\right) d x+\left(y^{2}-x^{2} \log \left(\frac{y}{x}\right)\right) d y=0\) (C.B.S.E. 2010 C)
Solution:
The given equation can be written as:

Question 19.
Solve the differential equation:
xdy-y dx= \(\sqrt{x^{2}+y^{2}}\) dx.
(iC.B.S.E. Sample Paper 2019)
Solution:
The given differential equation is:

Put y = vx, so that \(\frac{d y}{d x}\) = dv + x \(\frac{d v}{d x}\)
(1) becomes:

⇒ y+ \(\sqrt{x^{2}+y^{2}}\) = cx²,
which is the reqd. solution.

Question 20.
Prove that x² – y² = c(x² + y²)² is the general solution of the differential equation: (x³ – 3xy²)dx = (y³ – 3x²y)dy, where c is a parameter. (C.B.S.E. 2017)
Solution:
We have :(x³ – 3xy²) dx = (y³ – 3x²y)dy

∴ v³ – 3v = A(1 + v)(1 + v²) + B(1 – v) (1 + v²) + (Cv + D) (1 – v²).
Putting v= 1,
1-3 = A(2) (2)
⇒ A = -1/2

Putiing v = -1, -1 + 3 = B(2)(1 + 1)
⇒ B = 1/2

Putting v = 0
⇒ 0 = A(1)(1) + B(1)(1) + D(1)
⇒ 0 = \(-\frac{1}{2}+\frac{1}{2}\) + D
D = 0
Comparing coeff. of v³, 1 = A – B – C
⇒ C = A – B – 1 = \(-\frac{1}{2}-\frac{1}{2}\) – 1 = -2
∴ From (2),

Squaring , x² – y² = c’²(x²+ y²)²
⇒ x² – y² = c’² (x² + y² )²
where c’² = c,
which is the required solution.

Question 21.
Show that the differential equation:
2ye^x/y dx + (y – 2x e^x/y) dy = 0 is homogeneous and find the particular solution, given that x = 0 when y = 1. (C.B.S.E. 2013)
Solution:
(i) The given equation is :
2ye^x/y dx + (y – 2x e^x/y) dy = 0

Thus f(x, y) is homogeneous function of degree zero.

⇒ 2e^v = – log |y| + c
⇒ e^x/y = -log|y| + c …………….(2)

Now x = 0 when y = 1,
∴ 2(1) = -log |1| + c
⇒ 2 = – log 1 + c
⇒ 2 = —0 + c
⇒ c = 2.

Putting in (2),
2e^x/y = – log |y|+ 2,
which is the required solution.

Question 22.
Solve the differential equation:
(1 + x²)\(\frac{d y}{d x}\) + 2xy – 4x² =0, subject to the initial condition y (0) = 0. (C.B.S.E. 2019)
Solution:
The given equation can be written as :

Multiplying (1) by (1 + x²), we get:
(1 + x²)\(\frac{d y}{d x}\) + 2xy = 4x² dx
⇒ \(\frac{d}{d x}\) y.(1 + x²) = 4x²

Integrating, y.(1 + x²) = ∫ 4x² dx = \(\frac{4 x^{3}}{3}\) + C
⇒ y(1 + x²) = \(\frac{4}{3}\) x² + C …(2)
When x = 0, y = 0,
∴ C = 0 + C
⇒ C = 0.
ry 4 T
Putting in (2), y(1 + x²) = \(\frac{4}{3}\) x³ , which is the required solution.

Question 23.
Solve the differential equation :
\(\frac{d y}{d x}-\frac{2 x}{1+x^{2}} y\) = x² + 2 (C.B.S.E. 2019)
Solution:
The given equation is :

Hence, y = (1 + x²) (x + tan^-1 x + C).

Question 24.
Find the general solution of the following differential equation:
(1 + y²) + (x – e^tan-1y)\(\frac{d y}{d x}\) (C.B.S.E. 2016)
Solution:
The given equation is:


Putting xee^tan-1y = \(\frac{1}{2}\)e^2tan-1y + c
x = \(\frac{1}{2}\)e^tan-1y + c
which is the required solution.

Question 25.
(i) Solve the differential equation:
(tan^-1 y – x)dy = (1 + y²) dx. (N.C.E.R.T.; C.B.S.E. 2015)
(ii) Find the particular solution when x = 0, y = 0. (A.I.C.B.S.E. 2013)
Solution:
(i) The given equation can be written as :
\(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) …… (1)
Comparing with \(\frac{d x}{d y}\)+ Px = Q , we have:


which is the required solution.

(ii) When
x – 0, y = 0.
0 = (tan^-10 – 1) + ce-tan^-10,
⇒ 0 – (0 – 1) + ce^-0
⇒ 0 = – 1 + c
⇒ c = 1.
Putting in (3),
x = (tan^-1 y – 1) + e^-tan-1y,
which is the required particular solution.