Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 12 Linear Programming. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.
Class 12 Maths Chapter 12 Important Extra Questions Linear Programming
Linear Programming Important Extra Questions Very Short Answer Type
Question 1.
Draw the graph of the following LPP:
5x + 2y ≤ 10, x ≥ 0,y ≥ 0.
Solution:
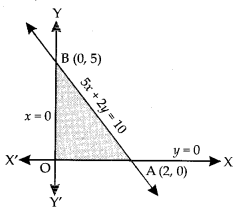
Draw the line AB : 5.v + 2y = 10 …(1),
which meets x-axis at A (2, 0) and y-axis at B (0,5).
Also x = 0 is y-axis and y = 0 is x-axis.
Hence, the graph of the given LPP is as shown (shaded):
Question 2.
Solve the system of linear inequations: x + 2y ≤ 10; 2x + y ≤ 8.
Solution:
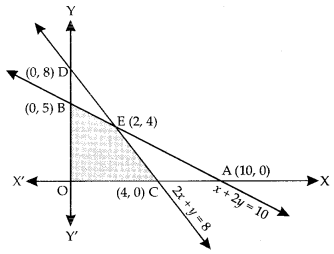
Draw the st. lines x + 2y = 10 and 2x + y = 8.
These lines meet at E (2,4).
Hence, the solution of the given linear inequations is shown as shaded in the following figure :
Question 3.
Find the linear constraints for which the shaded area in the figure below is the solution set:
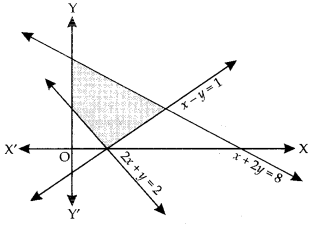
Solution:
From the above shaded portion, the linear constraints are :
2x + y ≥ 2,x – y ≤ 1,
x + 2y ≤ 8, x ≥ 0, y ≥ 0.
Question 4.
A small firm manufactures neclaces and bracelets. The total number of neclaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a neclace. The maximum number of hours available per day is 16. If the profit on a neclace is ₹100 and that on a bracelet is ₹300. Formulate an LPP for finding how many of each should be produced daily to maximize the profit ?
It is being given that at least one of each must be produced. (C.B.S.E. 2017)
Solution:
Let ‘x’ neclaces and ‘y’ bracelets be manufactured per day.
Then LPP problem is:
Maximize Z = 100x+300y
Subject to the constraints : x + y ≤ 24,
(1) (x) + \(\frac { 1 }{ 2 }\)y ≤ l6,
i.e. 2x + y ≤ 32
and x ≥ 1
and y ≥ 1
i.e. x – 1 ≥ 0
and y – 1 ≥ 0.
Question 5.
Old hens can be bought for ?2.00 each and young ones at ?5.00 each. The old hens lay 3 eggs per week and the young hens lay 5 eggs per week, each egg being worth 30 paise. A hen costs ₹1.00 per week to feed. A man has only ₹80 to spend for hens. Formulate the problem for maximum profit per week, assuming that he cannot house more than 20 hens.
Solution:
Let ‘x’ be the number of old hens and ‘y’ the number of young hens.
Profit = (3x + 5y) \(\frac { 30 }{ 100 }\) – (x + y) (1)
= \(\frac{9 x}{10}+\frac{3}{2}y\)x – y
= \(\frac{y}{2}-\frac{x}{10}=\frac{5 y-x}{10}\)
∴ LPP problem is:
Maximize Z = \(\frac{5 y-x}{10}\) subject to:
x ≥ 0,
y ≥ 0,
x + y ≤ 20 and
2x + 5y ≤ 80.
Linear Programming Important Extra Questions Very Long Answer Type 2
Question 1.
Maximize Z-5x + 3y
subject to the constraints:
3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0,y ≥ 0. (N.C.E.R.T)
Solution:
The system of constraints is :
3x + 5y ≤ 15 …(1)
5x + 2y ≤ 10 …(2)
and x ≥ 0, y≥ 0 …(3)
The shaded region in the following figure is the feasible region determined by the system of constraints (1) – (3):
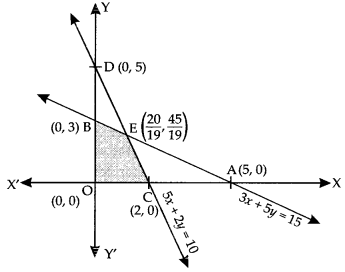
It is observed that the feasible region OCEB is bounded. Thus we use Corner Point Method to determine the maximum value of Z, where :
Z = 5x + 3y …(4)
The co-ordinates of O, C, E and B are (0, 0), (2,0), \(\left(\frac{20}{19}, \frac{45}{19}\right)\) (Solving 3x + 5y = 15 and 5x + 2y – 10) and (0, 3) respectively.
We evaluate Z at each comer point:
| Comer Point | Corresponding Value of Z |
| O: (0,0) | 0 |
| C: (2,0) | 10 |
| E(\(\left(\frac{20}{19}, \frac{45}{19}\right)\)) | \(\frac{20}{19}\) (Maximum) |
| B(0.3) | 9 |
Hence’ Zmax = at the Point \(\left(\frac{20}{19}, \frac{45}{19}\right)\)
Question 2.
Minimize Z = 3x + 2y subject to the constraints:
x +y ≥ 8, 3x + 5y ≤ 15, x ≥ 0, y ≥ 0. (N.C.E.R.T.)
Solution:
The system of constraints is :
x +y ≥ 8, , x ≥ 0, y ≥ 0…(1)
3x + 5y ≤ 15 …(2)
and x ≥ 0, y ≥ 0 …(3)
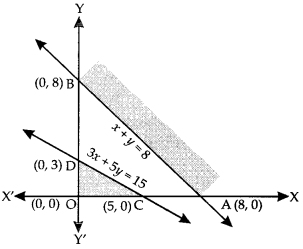
It is observed that there is no point, which satisfies all (1) – (3) simultaneously.
Thus there is no feasible region.
Hence, there is no feasible solution.
Question 3.
Determine graphically the minimum value of the objective function :
Z = – 50x + 20y
subject to the constraints:
2x-y ≥ – 5, 3x +y ≥ 3, 2x – 3y ≤ 12, x,y ≥ 0. (N.C.E.R.T.)
Sol. The system of constraints is :
2x-y ≥ – 5 …(1)
3x +y ≥ 3 …(2)
2x – 3y ≤ 12 …(3)
and x,y ≥ 0 …(4)
The shaded region in the following figure is the feasible region determined by the system of constraints (1) – (4).
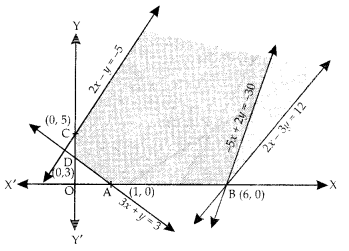
It is observed that the feasible region is unbounded.
We evaluate Z = – 50x + 20y at the corner points :
A (1, 0), B (6, 0), C (0, 5) and D (0, 3) :
| Corner Point | Corresponding Value of Z |
| A: (1,0) | -50 |
| B : (6, 0) | – 300 (Minimum) |
| C : (0, 5) | 100 |
| D : (0, 3) | 60 |
From the table, we observe that – 300 is the minimum value of Z.
But the feasible region is unbounded.
∴ – 300 may or may not be the minimum value of Z. ”
For this, we draw the graph of the inequality.
– 50x + 20y < – 300
i.e. – 5x + 2y < – 30.
Since the remaining half-plane has common points with the feasible region,
∴ Z = – 50x + 20y has no minimum value.
Question 4.
Minimize and Maximize Z = 5x + 2y subject to the following constraints : x – 2y ≤ 2, 3x + 2y < 12, -3x + 2y ≤ 3, x ≥ 0, y ≥ 0. (A.I.C.B.S.E. 2015)
Solution:
The given system of constraints is :
x – 2y ≤ 2 …(1)
3x + 2y < 12 …(2)
-3x + 2y ≤ 3 …(3)
and x ≥ 0, y ≥ 0.
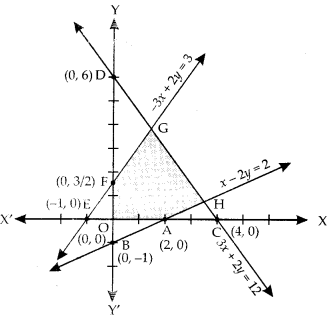
The shaded region in the above figure is the feasible region determined by the system of constraints (1) – (4). It is observed that the feasible region OAHGF is bounded. Thus we use Corner Point Method to determine the maximum and minimum value of Z, where
Z = 5x + 2y …(5)
The co-ordinates of O, A, H, G and F are :
(0, 0). (2. 0), (\(\frac{7}{2}, \frac{3}{4}\)) and (\(\frac{3}{2}, \frac{15}{4}\)), \(\frac { 3 }{ 2 }\))
respectively. [Solving x
2y = 2 and 3x + 2y = 12 for
H and -3x + 2y = 3 and
3x + 2y = 12 for G]
We evaluate Z at each cormer point:
| Corner Point | Corresponding value of Z |
| O: (0,0) | 0 (Minimum) |
| A: (2,0) | 10 |
| H(\(\frac{7}{2}, \frac{3}{4}\)) | 19 (Maximum) |
| G(\(\frac{3}{2}, \frac{15}{4}\)) | 15 |
| F: (0, \(\frac{3}{2}\))) | 3 |
Hence, Zmax = 19 at (\(\frac{7}{2}, \frac{3}{4}\)) and
Zmax = 0at (0,0)
Question 5.
A dealer in rural area wishes to purchase a number of sewing machines. He has only ₹5760.00 to invest and has a space for at most 20 items. An electronic sewing machine costs him ₹360.00 and a manually operated sewing machine ₹240.00. He can sell electronic sewing machine at a profit of ₹22.00 and a manually operated sewing machine at a profit of ₹18.00. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit. Make it a linear programming problem and solve it graphically. (C.B.S.E. 2014)
Solution:
Let ‘x’ be the number of electronic operated machines and ‘y’ that of manually operated machines be purchased.
Then the LPP problem is as follows :
Maximize:
Z = 22 + 18y
Subject to:
x + y ≤ 20 …(1)
360x + 240y ≤ 5760
i.e. 3x + 2y ≤ 48 …(2)
and x ≥ 0, y ≥ 0 …(3)
The shaded region of the figure represents the feasible region OCEB, which is bounded.
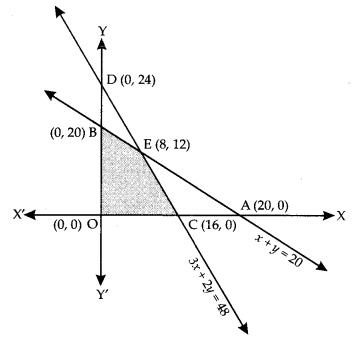
Applying Corner Point Method, we have:
| Corner Point | Corresponding value of Z |
| O: (0,0) C:(16,0) E: (8,12) B: (0,20) |
0 352 392 (Maximum) 360 |
Thus, Z is maximum at E (8, 12).
Hence, the dealer should invest in 8 electronic and 12 manually operated machines.
Question 6.
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 35 per package of nuts and ₹ 14 per package of bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day? Convert it into an LPP and solve graphically.
Solution:
Let ‘x’ and ‘y’ be the number of packages of nuts and bolts respectively.
We have the following constraints :
x ≥ 0 …(1)
y ≥ 0 …(2)
x + 3y ≤ 12 ….(3)
3x + y ≤ 12 …(4)
Now the profit,P= 35x+ 14y …..(5)
We are to maximize P subject to constraints (1) -(4).
Draw the line AB (x + 3y = 12)
Draw the line CD (3x + y = 12)
These meet at E (3, 3).
The shaded region in the figure represents the feasible region, which is bounded.
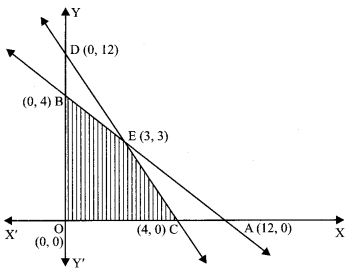
Applying Corner Point Method, we have :
| Corner Point | P = 35x + 14y |
| O: (0,0) | 0 |
| C : (4, 0) | 140 |
| E: (3,3) | 147 (Maximum) |
| B : (0,4) | 56 |
Hence, max. profit is ₹ 147 and it is obtained when 3 packages each of Nuts and Bolts are produced daily.
Question 7.
Two tailors A and B earn ₹ 150 and ₹ 200 per day respectively. A can stitch 6 shirts and 4 pants per day, while B can stitch 10 shirts and 4 pants per day. Form a L.P.P. to minimize the labour cost to produce (stitch) at least 60 shirts and 32 pants and solve it graphically.
Solution:
Let the tailor A work for ‘x’ days and B for ‘y’ days.

Thus, we have the following constraints:
x ≥ 0 …(1)
y ≥ 0 …(2)
6x + 10y ≥ 60
i.e. 3x + 5y ≥ 30 …….(3)
4x + 4y ≥ 32
i.e. x + y ≥ 8 ……(4)
The objective function, or the cost Z is:
Z = 150x + 200 y ……..(5)
For the solution set, we draw the lines:
x = 0, y – 0, 3x + 5y = 30, x + y = 8
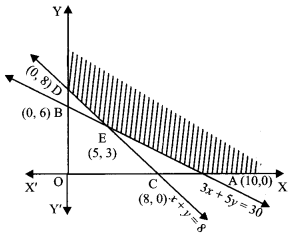
The feasible region (shaded) is unbounded. Let us evaluate Z at the comer points:
A (10,0), D(0, 8) and E(5, 3)
[Solving x + y – 8, Sx + 5y – 30; x – 5,y = 3]
Applying Comer Point Method, we have:
| Corner Point | Z = 150 x + 200y |
| A : (10, 0) E: (5,3) D: (0, 8) |
1500 1350 (Minimum) 1600 |
Hence, the tailor A should work for 5 days and B for 3 days.
To Check: Draw 150x + 200y < 1350 i.e. 3x + 4y < 27.
Since there is no region common with feasible region,
∴ Minimum value is ₹ 1350.
Question 8.
A dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. It costs ₹50 per kg to produce food I. Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C and it costs ₹70 per kg to produce food n. Formulate this problem as a LPP to minimise the cost of a mixture that will produce the required diet. Also find the minimum cost
Solution:
Let the quantity of Food I = x kg
and the quantity of Food II = y kg.
Then the LPP problem is as below :
Z = 50x+70y …(1)
Subject to 2x + y ≥ 8 …(2)
x + 2y ≥ 10 ….(3)
and x ≥ 0, y ≥0 ……..(4)
For the solution, we draw the lines :
x = 0,y = 0,2x + y = 8 and x + 2y = 10
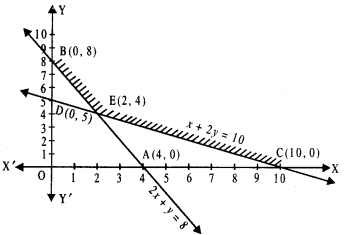
The feasible regin is as shown with vertices C(10,0), E(2,4) and B(0,8).
Applying Corner Point Method, we have
| Corner Point | Z = 50x + 70y |
| C: (10,0) E:(2,4) B: (0,8) |
500 380 (Minimum) 560 |
Thus minimum cost is ₹38Q when 2 kg of Food I and 4 kg of Food II are mixed.
Question 9.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 20 | 10 | 10 |
| B | 10 | 20 | 30 |
The machines I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively. The profit on each toy of type A is ₹50 and that of type Bis ₹60. Formulate the above problem as a LPP and solve it graphically to maximize profit.
(C.B.S.E. Sample Paper 2018-19)
Solution:
Let ‘x’ and ‘y’ be the number of toys of type A and type B respectively.
Then maximize :
P = 50x + 60y …(1)
Subject to constraints :
20x +10v ≤ 180 …(2)
10x + 20y ≤ 120 …….(3)
10x + 30y ≤ 150 ……(4)
and x ≥ 0, y ≥ 0 …(5)
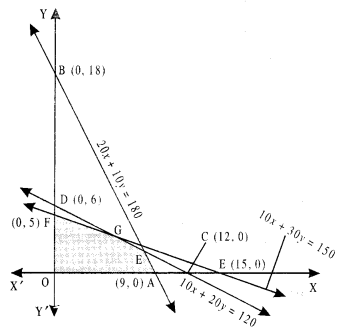
Applying Corner Point Method we have :
| Corner point | P = 50jc + 60y |
| O: (0,0) F:(0,5) G: (6,3) H: (8,2) A: (9,0) |
0 300 480 520 (Maximize) 450 |
Hence, maximum profit is ₹520 when x = 8 and y = 2. i.e., when 8 toys of type A and 2 toys of type B are made.
Question 10.
A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand- operated. It takes 4 minutes on the automatic and 6 minutes on the hand operated machines to manufacture a packet of screws ‘A’ while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a packet of screws ‘B\ Each machine is available for at most 4 hours on any day. The manufactures can sell a packet of screws ‘A’ at a profit of 70 paise and screws ‘B’ at a profit of ₹ 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit? Formulate the above LPP and solve it graphically and find the maximum profit (C.B.S.E. 2018)
Solution:
Let the factory manufacture ‘x’ of type ‘A’ and ‘y’ of type ‘B’
Clearly x ≥ 0 …(1)
and y ≥ 0 …(2)
Since the machines can operate for at the most 4 hours a day,
4x + 6y ≤ 240
i.e., 2x + 3y ≤ 120 …(3)
and 6x + 3y ≤ 240
i.e., 2x + y ≤ 80 …(4)
The objective function or the profit, P, is:
P = 0.7 x + y …(5)
We drawn the lines :
x = 0,y = 0,
2x + 3y = 120
and 2x + y – 80
The feasible region is shown shaded OCPB is bounded, where O is (0, 0), C is (40, 0), B is (0, 40) and P is (30, 20).
[Solving 2x + y – 80 and 2x + 3y = 120; x = 30, y – 20]
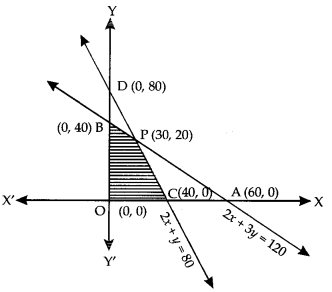
Applying Corner Point Method, we have :
| Comer point | P = 0.7x + y |
| O: (0, 0) C : (40, 0) P : (30, 20) B: (0,40) |
0 28 41 (Maximum) 40 |
Hence, in order to maximize profit 30 packets of screw ‘A’ and 20 packets of screw ‘B’ should be manufactured and maximum profit = ₹ 41.
Question 11.
A small firm manufactures chairs and tables. Market demand and available resources indicate that the continued production of chairs and tables should not exceed 50 units per day. It takes 30 minutes to manufacture a chair and 1 hour to manufacture a table. A maximum of 40 man-hours per day are available. The profit on each chair is ₹ 40 and profit on each table is ₹ 60. Determine how many each of chairs and tables should be manufactured per day in order to maximize the profit. What is the maximum profit? Formulate LPPand solve graphically.
Solution:
Let ‘x’ and ‘y’ be the number of chairs and tables respectively.
We have: x ≥ 0 ………..(1)
y ≥ 0 ………(2)
x + y ≤ 50 ……(3)
and \(\frac{x}{2}\) + y ≤ 40
⇒ x + 2y < 80 …(4)
The objective function, or the profit, Z is
Z = 40 x + 60 y …(5)
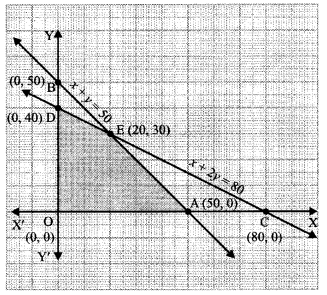
We have to maximize Z subject to (1) – (4).
For solution set, we draw the lines:
x = 0, y – 0, x + y = 50 and x + 2y – 80.
The lines x + y = 50 and x + 2y = 80 meet at E (20, 30).
The shaded portion represents the feasible region, which is bounded.
Applying Corner Point Method, we have:
| Corner Point | Z = 40x + 60y |
| 0 =(0,0) A: (50, 0) E: (20,30) B: (0,40) |
0 2000 2600 (Maximum) 2400 |
Hence, the maximum profit is ₹ 2600 when 20 chairs and 30 table are manufactured.