CBSE Class 11

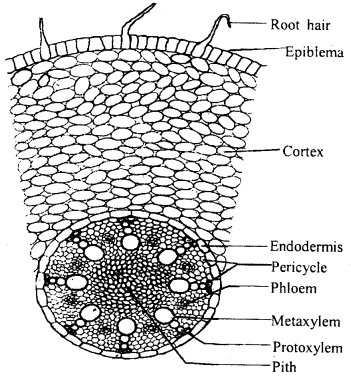
By going through these CBSE Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations Class 11 Notes, students can recall all the concepts quickly.

Complex Numbers and Quadratic Equations Notes Class 11 Maths Chapter 5

Imaginary Numbers: A number whose square is negative, is known as an imaginary number, e.g. : \(\sqrt{-1}, \sqrt{-2}\), etc.
\(\sqrt{-1}\) is denoted by the Greek letter i (iota).

Powers of i : i¹ = – 1; i²= – 1; i³ = — i, i⁴ = 1, etc.

An Important Result : For any two real numbers a and b,
\(\sqrt{a} \times \sqrt{b}=\sqrt{a b}\) is true only when at least one of a and b is either 0 or positive.
In fact, \(\sqrt{-a} \times \sqrt{-b}=(i \sqrt{a})(i \sqrt{b})=i^{2} \sqrt{a b}=-\sqrt{a b}\), where a and b are positive real numbers.

Complex Number : Any number of the form x + iy, where x, y are real numbers and i \(\sqrt{-1}\) is called a complex number.

It is denoted by z, i.e., z = x + iy. The real and imaginary parts of a complex number z are denoted by Re(z) and Im(z) respectively. Thus, if z = x + iy, then Re(z) = x and Im(z) = y.

Note : Every real number is a complex number, for if a e R, it can be written as a – a + i0.

Purely Real and Purely Imaginary Numbers : A complex number z is said to be
(i) purely real, if Im(z) = 0.
(ii) purely imaginary, if Re(z) = 0.

Conjugate of a Complex Number : The conjugate of a complex number z, denoted by \(\bar{z}\) is the complex number obtained by changing the sign of imaginary part of z i.e., if z = a + ib, then \(\bar{z}\) = a-ib.

Modulus of a Complex Number: The modulus of a complex number, z- a + ib, denoted by |z |, is defined as |z | = \(\sqrt{x^{2}+y^{2}}\)

Sum, Difference and Product of Complex Numbers : For any complex numbers z₁ = a + ib and z₂ = c + id, it is defined as
(i) Z₁ + z₂ = (a + ib) + (c + id) = (a + c) + i(b + d).
(ii) z₁ – z₂ = (a + ib) – (c + id) = (a -c) + i(b – d).
(iii) z₁z₂ = (a + ib)(c + id) = (ac -bd) + i(ad – bc).

Properties of Complex Numbers:

1. A real number can never be equal to an imaginary number.
2. (a + ib) = 0 ⇔ a = 0 and 6 = 0.
3. Two complex numbers are equal only when their real and imaginary parts are separately equal.
i.e., if a + ib = c + id, then a = c and b = d.

4. If z is a complex number, then :
(i) (\(\bar{z}\)) = z
(ii) (z + \(\bar{z}\)) is real.
(iii) (z – \(\bar{z}\)) is zero or an imaginary number.
(iv) z + \(\bar{z}\) = 2Re(z) and (z – \(\bar{z}\)) = 2iIm(z).
(v) z\(\bar{z}\) – |z |² and, therefore, z\(\bar{z}\) is real.

5. If z₁ and z₂ are complex numbers, then :
(i) \(\left(\overline{z_{1}+z_{2}}\right)=\overline{z_{1}}+\overline{z_{2}}\)
(ii) \(\left(\overline{z_{1}-z_{2}}\right)=\overline{z_{1}}-\overline{z_{2}}\)
(iii) \(\left(\overline{z_{1} z_{2}}\right)=\overline{z_{1}} \cdot \overline{z_{2}}\)
(iv) \(\left|z_{1} z_{2}\right|=\left|z_{1}\right|\left|z_{2}\right|\)

6. For any complex number z, |z | = 0 ⇔ z = 0.
7. The sum and product of two complex numbers are real if and only if they are conjugate of each other.
8. The conjugate and the reciprocal of a non-zero complex number z are equal if and only if | z | = 1.
9. Reciprocal or multiplicative inverse of a + ib
= \(\frac{1}{a+i b}=\frac{1}{a+i b} \times \frac{a-i b}{a-i b}=\frac{a}{a^{2}+b^{2}}-i\left(\frac{b}{a^{2}+b^{2}}\right)\)

10. For any integer k,
(i) i^2k = (-1)^k , i^{2k+ 1} = (- 1)^ki
(ii) i^4k = (i⁴)^k = 1, i^{4k+ 1} = i^4k+2 = i² = -1,
i^4k+3 = i³ = i² x i = -i

Geometrical Representation of a Complex Number : To every complex number z = x + iy, there is one and only one point P(x, y) in the plane, and conversely to every point (x,y) in the plane, there is one and only one complex number z = x + iy.

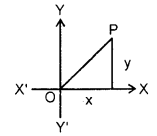
The plane, representing the complex numbers, as an ordered pair of real numbers is called the Complex plane or Gaussian plane or Argand plane.

Modulus and Amplitude of a Complex Number : Let a poin^ P represents a complex number z = x + iy in the complex plane. Then, the length OP is called the modulus of the complex number z and is denoted by |z|.

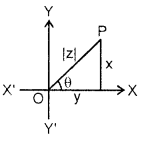
∴ |z| = OP = |x + iy|
= \(\sqrt{x^{2}+y^{2}}\) .

The angle XOP = θ is called the amplitude or argument of 2 and is written as amp. z or arg. z. The value of θ satisfying – π < θ < π is called the principal value of amp z.

Polar Form of a Complex Number : Let z – a + ib be represented by P(a, b).
Let OP = r, ∠XOP = θ.
Then, a – rcos θ,
b = rsinθ
= r² = a² + b²
⇒ r = |2|
and tanθ = \(\frac{b}{a}\)
⇒ cosθ = \(\frac{a}{r}\) ,sinθ = \(\frac{b}{r}\).
The form 2 = r(cos θ + isin θ) is called the Polar Form.

Polynomial Equation : A polynomial equation of a degree x has n roots.

Solutions of Quadratic Equation: The solutions of quadratic equation
ax² + bx + c = 0,
where a, b, c ∈ R, a ≠ 0, b2² – 4ac < 0 are given by
x = \(\frac{-b \pm\left(\sqrt{4 a c-b^{2}}\right) i}{2 i}\)

D = b² – 4ac is called the discriminant of the quadratic equation.

By going through these CBSE Class 11 Maths Notes Chapter 4 Principle of Mathematical Induction Class 11 Notes, students can recall all the concepts quickly.

Principle of Mathematical Induction Notes Class 11 Maths Chapter 4

Mathematical induction is a technique for proving general results or theorem involving positive integers.

The word induction means the method of inferring a general statement from the validity of particular cases.

Statement : A sentence which can be judged to be true or false is called a statement.
A statement holding for n ∈ N is generally denoted by P(n).

Principle of mathematical induction : Let P(n) be a statement involving the natural number n. Then,
(i) P( 1) is true and
(ii) P(k + 1) is true whenever P(k) is true, then P(n) is true for all natural numbers n.

For proving that statement P(n) holds for all n ∈ N :
Following steps are applied :

Step 1 : Verification that P(n.) holds for n = 1, i.e., P( 1) is true.
Step 2 : Suppose that P(re) holds for every k ∈ N.
Step 3 : Prove that P(n) holds for n = k + 1 also.

By going through these CBSE Class 11 Maths Notes Chapter 3 Trigonometric Functions Class 11 Notes, students can recall all the concepts quickly.

Trigonometric Functions Notes Class 11 Maths Chapter 3

Important Definitions:

Angle: An angle is considered as a figure obtained by rotating a given ray about its initial point. The original position of the ray is called the initial side and the final position is called the terminal side of the angle. The point of rotation is called the vertex.

Positive Angle : If the direction of the rotation is anticlockwise, the angle is said to be positive.

Negative Angle : If the direction of the rotation is clockwise, the angle is said to be negative.

Degree measure of an angle: If a rotation from initial side of the terminal side is (\(\frac{1}{360}\))th of a revolution, the angle is said to have a measure of one degree, written as 1°.

1° = 60′ [One degree = 60 minutes]
1′ = 60″ [One minute = 60 seconds]

Radian Measure : An angle with its vertex at the centre of a circle which intercepts an arc equal in length to the radius of the circle is said to have a measure of 1 radian.

Important Formulae:

1. θ = \(\frac{l}{r}\)
   where θ = angle subtended by arc of length l at the centre of the circle and
   r = radius of the circle.
2. π radians = 180°.
3. 1 radian = \(\left(\frac{180}{\pi}\right)^{\circ}\)
4. 1° = radian = 0.01746 (app.)

Circular Functions: Let a circle of unit radius be drawn with centre O. A line segment OP = 1 is rotated from the initial position OX, in the anticlockwise direction.

Let OP makes an angle θ with OX. The x-coordinate of P gives the value of cos θ and y – coordinate will give the value of sin θ. P may be any where on the circle and hence θ may acquire any value from 0 to 2π radians. Thus, we get the value of cos θ and sin θ for any value of θ.
These trigonometric functions are known as circular functions.

Important Formulae :

1. sin² θ – co² θ = 1
2. 1 + tan² θ = sec² θ
3. 1 + cot² θ = cosec² θ

Periodic Functions : A function f is said to be periodic, if there exists a real number T > 0 such that f(x + T) = f(x) for all values of x. Then, T is called the period of the function.
Trigonometric actions are also periodic.
Here, cos (2nπ + x) = cos x
sin (2 nn + x) = sin x

Trigonometric Ratios (T-Ratios) Of Angle (-x)

1. sin(-x) = -sin x,
2. cos (- x) = cos x,
3. tan (-x) = -tan x,
4. cosec (- x) = – cosec x,
5. sec(-x) = sec x,
6. cot (- x) = – cot x.

T-Ratios of (\(\frac{\pi}{2}\) – x)

1. sin (\(\frac{\pi}{2}\)-x) = cos x
2. cosec (\(\frac{\pi}{2}\)-x) = sec x
3. cos (\(\frac{\pi}{2}\)-x) = sin x
4. tan (\(\frac{\pi}{2}\)-x) = cot x
5. sec (\(\frac{\pi}{2}\)-x) = cosec x
6. cot (\(\frac{\pi}{2}\)-x) = tan x

T-Ratios of (\(\frac{\pi}{2}\) + x)

1. sin (\(\frac{\pi}{2}\)-x) = cos x
2. cos (\(\frac{\pi}{2}\)-x) = -sin x
3. tan (\(\frac{\pi}{2}\)-x) = -cot x
4. cosec (\(\frac{\pi}{2}\)-x) = sec x
5. sec (\(\frac{\pi}{2}\)-x) = -cosec x
6. cot (\(\frac{\pi}{2}\)-x) = -tan x

T-Ratios of (π -x)

1. sin (π – x) = sin x,
2. cos (π – x) = – cos x,
3. tan (π – x) = – tan x,
4. cosec (π – x) = cosec x,
5. sec (π – x) = – sec x,
6. cot (π – x) = – cot x.

T-Ratios of (π+ x)

1. sin (π + x) = – sin x,
2. cos (π + x) = – cos x,
3. tan (π + x) = tan x,
4. cosec (π + x) = – cosec x,
5. sec (π + x) = – sec x,
6. cot (π + x) = cot x.

T-Ratios of (2π – x)

1. sin (2π – x) = – sin x,
2. cos (2n – x) = cos x,
3. tan (2π – x) = – tan x,
4. cosec (2π – x) = – cosec x,
5. sec (2π – x) = sec x,
6. cot (2π -x) = – cot x.

T-Ratios of (2π + x)

1. sin (2π + x) = sin x,
2. cos (2π + x) = cos x,
3. tan (2π + x) = tan x,
4. cosec (2π + x) = cosec x,
5. sec (2π + x) = sec x,
6. cot (2π+x)=cotx.

Note : To learn these formulae by heart, we adopt the following method :

I. First of all, we determine the sign of t-ratio under consideration.
The phrase Add Sugar To Coffee is quite helpful. We write Add, Sugar, To,
Coffee in I, II, III, IV quadrants respectively.

1. The letter A of word ‘add’ indicates all the f-ratios of angles lying in the first quadrant are positive.
2. The letter S of word ‘sugar’ indicates sin and cosec of the angle lying in II quadrant are positive and rest of t-ratios are negative.
3. T of word ‘to’ indicates tan and cot of the angle lying in the third quadrant are positive and rest of the t-ratios of such angles are negative.
4. C of the word coffee shows that cos and sec of the angles lying in IV quadrant are positive and rest of t-ratios are negative of such angles.

II. (i) For -angle – x, π – x, π + x, 2π – x, 2π + x, the t-ratios remains to be the same.
sin (- x) = – sin x, tan (π + x) = tan x, cos (2π -x) = cos x.

(ii) For angles \(\frac{\pi}{2}\) – x, \(\frac{\pi}{2}\) + x, \(\frac{3\pi}{2}\) – x, \(\frac{3\pi}{2}\)+ x the t-ratio changes from cos to sin , tan to cot and sec to cosec and vice versa.
e.g., sin(\(\frac{\pi}{2}\) + x) = cosx, tan(\(\frac{\pi}{2}\) – x) = cot x,
sec(\(\frac{\pi}{2}\) + x) = -cosec x etc.

T-Ratios of (x + y)

1. sin (x + y) = sin x cos y + cos x sin y
2. cos (x + y) = cos x cos y – sin x sin y
3. tan (x + y) = \(\frac{\tan x+\tan y}{1-\tan x \tan y}\)
4. cot(x + y) = \(\frac{\cot x \cot y-1}{\cot x+\cot y}\)

T-Ratios of (x – y)

1. sin Or – y) = sin x cos y – cos x- sin y
2. cos (x -y) = cos x cos y + sin x sin y
3. tan(x – y) = \(\frac{\tan x-\tan y}{1+\tan x \tan y}\)
4. cot(x – y) = \(\frac{\cot x \cot y+1}{\cot y-\cot x}\)

T-Ratios of (2x)

1. sin 2x = 2sin x cos x = \(\frac{2 \tan x}{1+\tan ^{2} x}\)
2. cos 2x = cos² x – sin² x = 2cos² x – 1 = 1 – 2sin² x
   = \(\frac{1-\tan ^{2} x}{1+\tan ^{2} x}\)
3. tan 2x = \(\frac{2 \tan x}{1-\tan ^{2} x}\)

T-Ratios of (3x)

1. sin 3x = 3sin x – 4sin³ x.
2. cos 3x = 4cos³ x – 3 cos x.
3. tan3 x = \(\frac{3 \tan x-\tan ^{3} x}{1-3 \tan ^{2} x}\)

Sum and Difference of two like ratios :

1. sm x + sin y = 2sin\(\frac{x+y}{2}\) cos \(\frac{x-y}{2}\)
2. sin x – sin y = 2cos \(\frac{x+y}{2}\) sin \(\frac{x-y}{2}\)
3. cos x + cos y = 2cos \(\frac{x+y}{2}\) cos\(\frac{x-y}{2}\)
4. cos x – cos y = – 2sin\(\frac{x+y}{2}\) sin\(\frac{x-y}{2}\)

Product of T-Ratios:

1. 2 sin x cos y = sin (x + y) + sin (x – y).
2. 2 cos x sin y = sin (x + y) – sin (x – y).
3. 2 cos x cos y = cos (x + y) + cos (x – y).
4. 2 sin x sin y = cos (x – y) – cos (x + y).

General solution of an equation :

1. If sin x = 0, then x = nπ, n ∈ Z.
2. If cos x = 0, then x = (2n + 1)\(\frac{\pi}{2}\), n ∈ Z.
3. If tan x = 0, then x = nπ, n ∈ Z.
4. sin x = sin y ⇒ x = nπ + (- 1 )ⁿy, n ∈ Z.
5. cos x = cos y ⇒ x = 2nπ ±y, n ∈ Z.
6. tan x = tan y ⇒ x = nπ+y, n ∈ Z,
   where y is the principal value of x.

Here we are providing Class 11 Biology Important Extra Questions and Answers Chapter 6 Anatomy of Flowering Plants. Important Questions for Class 11 Biology are the best resource for students which helps in Class 11 board exams.

Class 11 Biology Chapter 6 Important Extra Questions Anatomy of Flowering Plants

Anatomy of Flowering Plants Important Extra Questions Very Short Answer Type

Question 1.
Which structure originates the lateral roots?
Answer:
Pericycle

Question 2.
What are Casparian strips?
Answer:
These are thickenings of lignin and suberin formed around the artificial walls of the endodermis to prevent plasmolysis.

Question 3.
Give an example of anomalous secondary growth.
Answer:
Bougainvillaea.

Question 4.
Name the type of wood in which vessels are absent.
Answer:
Softwood, e.g. Pinus.

Question 5.
Give an example of thick-walled parenchyma cells.
Answer:
Xylem Parenchyma in secondary tissue.

Question 6.
Which type of vascular bundles are found in Cucurbita.
Answer:
Bicollateral.

Question 7.
What are the meristematic tissues?
Answer:
They are a perpetually juvenile group of cells with the indefinite power of division.

Question 8.
What is the function of Kasparian strips?
Answer:
To prevent loss of water and minerals back to the cortex.

Question 9.
What is the function of tracheids?
Answer:
Tracheids transport water and give mechanical support to the tree.

Question 10.
What are tyloses?
Answer:
They are the vessels of hardwood containing bladder like ingrowth in the pores of lateral walls.

Question 11.
What is ring porous?
Answer:
It is a wood containing vessels of large and small sizes in distinct parts of annual rings.

Question 12.
Why do xerophytic leaves have multilayered give rise to the new plant?
Answer:
To minimize the transpiration.

Question 13.
What is diffuse-porous?
Answer:
It is a wood containing vessels of the same size in late and early.

Question 14.
What is the role of lenticel?
Answer:
It causes gaseous exchange between the atmosphere and living cells.

Question 15.
What are the functions of Tracheids?
Answer:
Tracheids transport water and give mechanical support to the tree.

Question 16.
Which tissue forms the pericycle in the dicot stem?
Answer:
Sclerenchyma tissue.

Question 17.
What is the advantage of Iigno-cellulose in the walls of the xylem?
Answer:
It provides mechanical support.

Question 18.
What uses are phloem fibres put to?
Answer:
They are used for making ropes, coarse textiles and heads.

Question 19.
Why do we notice it feasible to do grafting in monocot plants?
Answer:
Because they lack vascular cambium.

Question 20.
Name the type of plant tissue that has thin-walled cells with 12 – 140 sides and retain, the ability of division at maturity.
Answer:
Parenchyma.

Question 21.
What is phellogen?
Answer:
It is cork cambium which cuts cells upper side and lower side. The upper side cells from the phellem and lower phellogen and phelloderm constitute the periderm.

Anatomy of Flowering Plants Biology Important Extra Questions Very Short Answer Type

Question 1.
What are tracheary elements? Of what use are these to the plants?
Answer:
These are vessels and tracheids. They are conducting cells of the xylem. The xylem vessels have perforations in their end walls while perforations are absent in tracheids, they form a continuous channel through the root, stem and leaves for the conduction of water and minerals.

Question 2.
If you are provided with microscopic preparation of transverse sections of a meristematic tissue and permanent tissue, how would you distinguish them apart?
Answer:
Meristematic tissues are composed of cells that are always in a dividing stage and divide endlessly to form new cells. These cells exist in different shapes without any intercellular spaces. These cells are thin-walled, rich in protoplasm and active with large nuclei and without vacuoles.

Permanent tissues are derived from meristematic tissue and are composed of cells, which have lost the power of division. These cells have their definite shape, size and function. These cells may be thin-walled or thick-walled.

Question 3.
What are the three basic tissues systems in Howering plants? Name the tissues under each system.
Answer:
In flowering plants, the three basic tissue systems are:
(a) DermalIt comprises the epidermis which is protective in function. During secondary growth, it is replaced by periderm.

(b) Vascular tissue system It consists of xylem and phloem and is found in the stele. In the root, the vascular bundles are renal with exarch condition whereas, in the stem, these are collateral with each condition.

(c) Ground or Fundamental Tissue It includes all the tissues except dermal and vascular, as parenchyma and sclerenchyma. It is found mainly between the epidermis and vascular cylinder and is formed of thin-walled cells with intercellular spaces in between them. Collenchyma is usually found to be thickened at the comers whereas currency nations are dead tissue and provide mechanical support.

Question 4.
Describe the structure and functions of the primary xylem.
Answer:
The primary xylem consists of tracheids vessels, xylem parenchyma and xylem fibres. The tracheids are elongated with tapering ends. They provide strength as well as help in absence of sap from roots to the leaves. The vessels are composed of a row of cells with large perforations at both ends but no bordered pits.

They help in the conduction of water and minerals and help in the storage of food. The xylem fibres are made up of sclerenchymatous cells associated with the xylem and they provide mechanical support to the plant body.

Question 5.
Why do we notice distinct rings in the tree of the temperate region while the tree of the coastal area is not distinct?
Answer:
The climatic conditions affect largely the activity of the cambium. It temperate region, the. cambium activity varies and it is not uniform throughout the year. But in coastal areas, it remains uniform throughout the year. Thus, due to the periodical activity of cambium in the temperate region, we notice distinct rings of spring and winter wood and not in the coastal area.

Question 6.
What is heartwood? Mention its any three characteristics.
Answer:
Heartwood: The hard central region of a tree trunk made up of xylem vessels that do not take part in the conduction of water.

Three characteristics of heartwood:

1. It is a non-functional and dead position.
2. It is dark coloured and filled with resins, tennis etc.

Question 7.
Point out the limitations of wood.
Answer:
Limitations of Wood:

• It does not change its physical and mechanical properties while heating.
• It cannot be changed into new shapes and forms.
• It is least resistant to infection caused by microorganisms and decay.
• It is combustible

Question 8.
What value is the study of plant anatomy?
Answer:
It helps to get the knowledge of plant structure and to solve various taxonomic problems. The determination of various adulterants in spices coffee, tea vegetable, dyes, tobacco saffron, as asafoetida is possible only when one knows about the anatomy of this substance.

Pharmacology and Pharmacology are dependent upon anatomical studies to know about the drug plants and their actions. It also helps in forming spurious materials from the standard woods. It also helps forensic experts fro solving criminal cases.

Question 9.
How is a cambial ring formed in dicotyledonous roots?
Answer:
Formation of the cambial ring in dicot roots: Perennial dicotyledonous root show secondary growth due to secondary meristems. Some parenchymatous cells in the phloem become meristematic. They divide and forms cambium strips there. External to the xylem a cambial ring is formed.

This lies on the inner side of the phloem cells and is cut off from the cambium on the inner and outer sides. Inner side cells form secondary xylem while the outer side cells of the cambium form secondary phloem. The primary phloem comes on the outside and the cambium forms a complete ring.

Question 10.
What are the permanent tissues?
Answer:
The permanent tissue is derived from meristematic tissues as the result of division and differentiation. They are composed of cells, which have lost the power of dividing. These cells have their definite shape, size and function. These cells may be thin-walled or thick-walled.

Question 11.
Are there any tissue elements of the xylem which are comparable to those of phloem? Comment.
Answer:

1. The sieve elements of the phloem are comparable to the vessel of the xylem because both lack nucleus at maturity.
2. Phloem fibre is similar to xylem fibre because both provide tensile strength to the tissue.

Phloem parenchyma and xylem parenchyma is the living components of phloem and xylem respectively.

Question 12.
Answer the following with reference to the anatomy of the monocot stem.
(i) How are the vascular bundles arranged?
Answer:
The vascular bundles are scattered in the ground tissue.

(ii) How are the xylem vessels arranged in each bundle? What do you call such an arrangement?
Answer:
Xylem vessels are ‘Y’ shaped. The big metaxylem vessels with pitted thickening from the arms, of Y. Protoxylem, occupies the lower arm of Y and is composed of spiral thickening.

But the vascular bundles are conjoint, collateral, closed and Endarch.

(iii) Vascular bundles are closed ones. What type of tissue is lacking in them?
Answer:
Cambium is absent.

Question 13.
What is phellogen? What does it produce?
Answer:
Phellogen is a cork cambium that is developed front hypodermis and epidermal cells near to the cortex. It is produced in the dicot stem during secondary growth for providing protection to the inner tissues.

It produces cork towards the outside and secondary cortex towards the inside.

Question 14.
What features make wood unique as a material?
Answer:
The following features make the wood unique as a material:

1. As it is light in weight, it can be easily transported over long distances.
2. It is a bad conductor of heat, electricity and sound.
3. It is resistant to rust.
4. It can be moulded into various desirable shapes.
5. The fluctuation in temperature does not affect largely and the volume of the wood.
6. Wood pulp is used for the synthesis of various materials like paper, plastics, rayon and transparent films.

Question 15.
List few important anatomical characteristics of the xerophytic leaf.
Answer:
The anatomical characteristics of the xerophytic leaf are:

1. The presence of a thick cuticle on both the epidermis of the leaf offers protection and reduces the rate of transpiration.
2. A multilayered epidermis is present. Its cells are elongated and lignified.
3. Stomata remain sunken in the lower epidermis. This reduces the rate of transpiration.
4. Palisade tissues are richly filled with chloroplast.
5. It also contains crystals of calcium oxalate scattered in the upper palisade tissues of leaf cells.

Question 16.
List the differences between the internal structure of the dicot stem and the Monocot stem.
Answer:

Anatomy of Flowering Plants Biology Important Extra Questions Very Short Answer Type

Question 1.
What are the characters of collenchyma tissues? Give its functions also.
Answer:
Collenchyma tissue: Collenchyma tissue cells are living isodiametric without any intercellular spaces. The comer walls are thickened by Pectinisation. They appear cylindrical in vertical section and oval or polygonal in cross-section. The nucleus in each cell lies at a comer position.

Collenchyma

They are found in the dicot stem below the epidermis and on the outer region of the leaf, midribs and pedicels. On the basis of thickening, they are of three types:

1. Lamellar,
2. Angular,
3. Lacunate

Functions: Collenchyma tissue provides mechanical function as well v as the function of photosynthesis.

Question 2.
Draw a well-labelled diagram showing the L.S.of phloem of an angiosperm with its components.
Answer:
Phloem is a food conducting tissue and it consists of:

1. Sieve, elements
2. Companion cells
3. Phloem fibres and
4. Phloem parenchyma.

1. Sieve elements: These occur as a single cell in pteridophytes and gymnosperms and longitudinal file of cells in angiosperms. The morphological specialization of sieve plates is the development of sieve area on their walls bearing sieve plates. The sieve plate bears a large number of perforations.

The protoplasmic strands maintain continuity through these perforations within the adjoining sieve tubes. In a mature sieve element there occurs a thin layer of parietal cytoplasm and a large central vacuole. The most important features of sieve elements are that they lack a nucleus at maturity.

Structure of phloem (L.S)

2. Companion cells: These are thin-walled, living parenchyma narrow cells, which are closely associated with sieve tube elements. They appear rounded or polygonal with dense granular cytoplasm, « prominent nucleus and numerous small vacuoles. The companion cells lack starch.

The nuclei of the companion cells serve as the nucleus of sieve tubes as they lack them. The companion cells mainly occur in angiosperms, ac¬companying the sieve tube elements.

3. Phloem fibres: They form a prominent part of both the primary and secondary phloem. They are elongated cells with lignified walls having simple pits. They provide support and help in the transport of food material. They are used for making cords and ropes etc.

4. Phloem parenchyma: These are the living parenchyma cells associated with sieve tube cells. They are elongated with sieve tube cells. They are elongated, pointed in shape and store the starch, fat and other organic substances. The tannings and resins are also found in these cells, They are elongated like the sieve elements.

The sieve element is a living component, which lacks a nucleus at maturity.

Question 3.
Describe briefly the various types of vascular bundles.
Answer:
These are of the following types:
1. Radial The bundles in which xylem and phloem are arranged on different adulterating with each other and form the separate bundles are called radial vascular bundles as in all roots.

2. Conjoint The xylem and phloem are situated at the same radius and form a vascular bundle together.

These are divided into three types:
(a) Collateral: These are the bundles where xylem and phloem are arranged on some radius, xylem is located internally and phloem externally. These may be open when there is a patch of cambium in between the xylem and phloem e.g. Helianthus or closed when there is no cambium at all as seen in monocot stems

(b) Bicallatiral: In this vascular bundle, the phloem is found in two groups one outside the xylem elements and the other inner to them. These are always open and found in pumpkin.

(c) Concentric: The bundle in which either Phloemounds the phloem completely is known as concentric.

This exists in two forms.

1. Anphicribral: The xylem lies at the centre and is surrounded by a ring of phloem, e.g., fern.
2. Amphivaial: The phloem lies at the centre and is surrounded by the xylem e.g. Dracaena.

Question 4.
Describe briefly the internal structure of the monocot root with the help of a labelled diagram.
Answer:
A transverse section of the monocot root shows the following issues.

1. It is composed of a single layer of compactly arranged thin-walled cells without intercellular spaces and cuticle. It bears many unicellular root hair.
2. Cortex: It is present beneath the epidermis. It consists of 15-20 layers of parenchymatous cells with large intercellular spaces.
3. Endodermis: It is the innermost layer of the cortex. Its cells are barrel-shaped with Casparian strips on their anticlinal walls. The passage cells are seen just opposite the protoxylem ends.
4. Pericycle: It consists of a single layer of thin-walled parenchymatous cells.
5. Vascular bundle: The vascular bundles are radial and the xylem is exarch. The xylem and phloem bundles are always more than six.
6. Pith: It occupies the central portion of the stele and is made up of parenchymatous cells.
7. Conjunctive tissue: It consists of parenchymatous cells and is found between the xylem and phloem strands.
   
   T.S. of a typical monocot root

Question 5.
Define the following.
(i) Radial vascular bundles
Answer:
Radial vascular bundles: The bundles in which xylem and phloem are arranged in different radii alternating with each other and form the separate bundles are called radial vascular bundles as in all roots.

(ii) Collateral vascular bundles
Answer:
Collateral vascular bundles: These are the bundles where xylem and phloem are arranged not at the same radius. Xylem is located internally and phloem externally. These may be open when there is a patch of cambium in between the xylem and phloem e.g. Helianthus or closed when there is no cambium at all as seen in the monocot stem.

(iii) Exarch xylem
Answer:
Exarch xylem: It is the condition where protoxylem is located towards the periphery of axis and metaxylem inwards e.g. root.

(iv) Endarch xylem
Answer:
Endarch xylem: It is the condition where metaxylem is located towards the periphery of axis and protoxylem inwards e.g. stem.

(v) Stele
Answer:
Stele: All the tissues that lie internal to Endoolerinis are collectively called stele. The outermost layer of stell is known as the pericycle.

Question 6.
Distinguish between:
(i) Phiilem and Pheiloderm
Answer:
Phiilem: It is a dead tissue that is formed by the activity of cork cambium in the outer region of the cortex during secondary growth. It is protective in function.

Pheiloderm: It is a living tissue that is formed by the activity of cork cambium in the inner side of the cortex. It regains during secondary growth. If performs the function of storage.

(ii) Open bundle and closed bundle
Answer:
Open Bundle: Avascular bundle containing cambium between xylem and phloem is called an open bundle e.g. dicot stem.

Closed Bundle: Avascular handle lacking cambium between xylem and phloem is called a closed bundle e.g. monocot stem.

(iii) Fascicular cambium and inter fascicular cambium
Answer:
Fascicular cambium: It is a strip of cambium found between the xylem and phloem of each vascular bundle of dicot stem.

Interfascicular cambium: It is a strip of cambium that is formed from the cells of medullary rays adjoining with the fascicular cambium. It occurs dining secondary growth.

(iv) Conjoint vascular bundles and Radial vascular bundles
Answer:
Conjoint vascular bundles: Xylem and phloem lie in the same bundles. They lie on different radii alternating with each other e.g. Dicot and monocot root.

Radial vascular bundles: Xylem and phloem lie in separate bundles. They lie on different radii alternating with each other e.g. Dicot and monocot root.

(v) Periderm and Bark
Answer:
Periderm: It includes three tissue consisting of phellogen, phellem and phelloderm and is formed at the peripheral region of the axis.

Bark: It includes all the tissue external to the secondary xylem formed during secondary growth. These are cambium, secondary phloem.

By going through these CBSE Class 11 Maths Notes Chapter 1 Sets Class 11 Notes, students can recall all the concepts quickly.

Sets Notes Class 11 Maths Chapter 1

Set: Any well-defined collection of objects, which are different from each other, and which we can see or think of is called a set.

Members of a set: The objects which belong to a set are called its members or elements.

Representation of a set: There are two ways by which the , sets can be represented :
(a) Tabular form or Roster form : Here, the elements of a
set are actually written down, separated by commas and enclosed * within braces (i.e., curly brackets). Thus,

(i) V, the set of vowels in the English alphabet = {a, e, i, o, u},
(ii) A, the set of odd natural numbers < 10 = {1, 3, 5, 7, 9),
(iii) N, the set of natural numbers = {1, 2, 3,…}.

(b) The set builder form : In this form, we list the property or properties satisfied by the elements of the set. Thus,
(i) M = {2, 3,.5, 7, 11, 13, 17, 191 = {x : x is a prime number < 20).

(ii) A = 16, 7, 8, 9, 10, 11} = {x| ∈ N, 5 < x < 12}, where ∈ stands for ‘belongs to’ and ‘ | ’ stands for ‘such that’.

It may be noted that while writing the set in roster form, an element is not generally repeated. For example, the set of letters of the word ‘SCHOOL’ is (S, C, H, O, L}.

Empty set or null set or void set : A set consisting of no element at all is called the empty set or the null set or the void | set. It is denoted by Φ (Phai). In roster form, it is written as = { }.
Examples : (i) (x : x ∈ N, 1 < x < 2} = Φ.
(ii) {x : x ∈ R, x² = – 1} = Φ.

Finite Set: A set in which the process of counting of elements surely comes to an end, is called a finite set.
Examples : ii) {x : x ∈ N, x < 500) (ii) Set of all trees on earth.

Infinite Set: A set, in which the process of counting of elements never comes to an end, is called an infinite set. Examples : (i) {x : x ∈ N, x > 50), (ii) {x : x ∈ Z, x < 1}.

Equal Sets : Two sets A and B are said to be equal, if every element of A is in B and every element of B is in A. It is written as A = B.
Examples: (i) {1, 2, 5} = {2, 1, 5} = {5, 1, 2)
(ii) {1, 2, 3, 1} = {1, 2, 3} = {1, 1, 2, 2, 3} etc.
[∵ The repetition of elements in a set is meaningless]

Equivalent Sets : Two finite sets A and B are said to be equivalent, if n(A) = n(B), where n(A) or n(B) is the number of elements in set A or B. It is written as A ↔ B.
Example: If A = {1, 2, 3} and B = {a, b, c}. Then, A ↔ B as n(A) = n(B) = 3.

Whenever A = B, then n(A) = n(B). Thus, equal sets are always equivalent. But, equivalent sets need not be equal.

Disjoint Sets : Two sets are said to be disjoint, if they have no element in common.
Example : A = {1, 3, 5} and B = {2, 4, 6) are disjoint sets.

Subset: If A and B are two sets given in such a way that every element of A is in B, then A is a subset of set B and it is written as A ⊂ B (read as ‘A is contained in B’)
If at least one element of A does not belong to B, then A is not a subset of B. It is written as A ⊄ B.
Example : If A = {1, 2, 3} and B = {3, 2, 4, 1), then A ⊂ B.

Subsets of Set of Real Numbers R :
There are many important subsets of R. Some of them are given below :
(i) The set of natural numbers = N = {1, 2, 3, 4, 5, ….)

(ii) The set of integers Z is
Z = {…., – 3, – 2, – 1, 0, 1, 2, 3, ….}

(iii) The set of rational numbers Q.
Q = {x: x = \(\frac{p}{q}\), p,q ∈ Z and q ≠ 0

(iv) Set of irrational numbers
T = {x : x e R and x ∉ Q} = R – Q.

Members of T are such as √2, √5, √7,…., π, etc.
Here, we observe that
N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, N ⊄ T.
INTERVAL AS SUBSET OF R.
Let a, b ∈ R and a < b.

Open Interval : The set of real numbers {y : a <y < b} is called an open interval and is denoted by (a, b). Here all the points between a and b belong to the open interval (a, b), but a and b do not, belong to this interval.

Closed Interval: Closed interval is defined as {a, b = [x : a ≤ x ≤ b}.
All the points between a and b and the points a and b belong to \a,b).

Closed on the left and open to right: [a, b) = {x:a ≤ x < b}.
All the points between a and b and the point a belong to fa, b) but b does not belong to this interval.

Open on the left and closed to the right:
(a, b] = {x:a < x ≤ b}.
All the points between a and b and the point b belong to (a, 6] but a does not belong to it.

Super Set: If A is subset of B, then we say that B is a super set of A and is written as B ⊃ A.’

Some results on subsets :

• Every set is a subset of itself, i.e.,A⊂A, B⊂B, etc.
• The empty set is a subset of every set, i.e., Φ ⊂ A, Φ ⊂ B, etc.
• If A = B, then A ⊂ B and B ⊂ A.
• If A ⊂ B and B ⊂ A, then A = B.
• If A contains n elements, then A has 2ⁿ subsets.

Power Set : The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set.

Proper Subset : If A is a subset of B but A ≠ B, then A is called a proper subset et P and is written as A ⊂ B. Thus, A is a proper subset of B only when every elemént of A is in B and B has at least one extra element than A.

Example: If A {1, 2. 3) and B = (1, 2, 3, 4). Then, A ⊂ B and A ≠ B. Therefore A ⊂ B.

Note : If A is a subset of B and A = B, then A is not a proper subset of B. In such a case, it is denoted as A ⊆ B.

Some results on proper subsets:

• If A ⊂ B and A ≠ B, then A ⊂ B.
• No set is a proper subset of itself.
• Φ is a proper subset of every set except itself.
• Φ has no proper subset.
• A set having n elements has (2ⁿ – 1) proper subsets.

Universal Set : If there are some sets under consideration, then there happens to be a set which is a superset of each one of the given sets. Such a set is called the universal set and it is denoted by U or ξ

Venn Diagrams : Most of the relationships between sets can be represented by means of diagrams. Figures representing sets in the form of enclosed region in the plane are called Venn diagrams. In these diagrams, the universal set is usually represented by a rectangular region and its subsets by bounded regions inside this rectangular region.

Venn Diagrams In Different Situations

1. A ⊂ U, where U is the universal set.

2. Two intersecting subsets of a universal set U.

3. Two disjoint subsets of a universal set U.

4. A⊂B⊂U, where U is the universal set.

Operation of sets : The main set operations are

1. Union of sets
2. Intersection of sets
3. Difference of sets.

Union of two sets: The union of two
sets A and B, denoted by A u B (read as A union B), is the set of all those elements which are either in A or in B or in both.

Symbolically:
A∪B = {x:x ∈ A or x ∈ B}.
Example: If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Then,
A ∪ B = {1, 2, 3, 4}∪{2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}.

Some results on union of sets :

• A⊂A⊂B and B⊂A∪B.
• If A ⊂B, then A∪B⊂B.

Intersection of sets : The intersection of two sets A and B, denoted by A ∩ B (read as A intersection B), is the set of all elements common to both A and B.

Symbolically:
A ∩ B=[x:x ∈ A and x ∈ B).
Example: If A = (1, 2, 3, 4} and B = {2, 4, 6, 8). Then,
A ∩ B = (l, 2,3, 4}∩{2, 4, 6,8} = {2, 4}.

Disjoint Sets : Two sets A and B are said to be disjoint, if A ∩ B = Φ. ,
If A ∩ B ≠ Φ, then A and B are called overlapping or intersecting sets.

Difference of two sets : The difference of two sets A a.nd B, denoted by A – B (read as A minus B), is the set of all those elements of A which are not in B.

Symbolically :
A-B = {x:x∈A and x ∉ B}.
Example: If A = {1, 2, 3, 4, 6, 12} and B = {1, 2, 4, 8, 16). Then,
A – B = {3, 6,12} and B – A = {8, 16}.
Note : In general A – B ≠ B – A.

Laws of Set Operations:

1. Commutative Laws : For any two sets A and B, we have :
(i) A∪B = B∪A (ii) A ∩ B = B ∩ A.

2. Associative Laws: For any three sets A, B and C, we have :
(i) (A∪B)∪C = A∪(B∪C), {ii) (A∩B)∩C = A∩(B∩C).

3. Distributive Laws : For any three sets A, B and C, we have:
(i) A∪(B∩C) = (A∪B)∩(A∪C).
(ii) A∩(B∪C) = (A∩B)∪(A∩C).

4. Idempotent Laws : If A is any set, then
(i) A∩A = A (ii) A∪A = A,

5. Identity Laws : If A is any subset of a universal set U and Φ is the null set, then
(i) A∩U = A (ii) A∩Φ = Φ
(iii) A∪Φ = A (iv) A∪U = U.

Complement of a set : If U be a Universal set and A is the subset of U, then complement of A with respect to U, denoted by A’ or A^c, is defined as A’ = {x 😡 ∈ U and x ∉ A}, i.e., the complement of A is the set of elements of U which are not the elements of A.

Properties of Complements:
(i) Complement Laws.
(a) A∪A’ = U (b) A∩A’ = Φ

(ii) De Morgan’s Laws.
(a) (A ∪ B)’ = A’∩ B’ (b) (A∩B)’=A’∪B’

(iii) Law of double Complementation (a)(A’)’ = A

(iv) Complement of Φ and ∪
(a) Φ’ = U (b) U’ = Φ.

Cardinal Number : n, the number of elements in a set is called the cardinal number of the set, denoted by n(A).

Example : A = {1, 2, 3, 4, 5} n(A) = 5, since A has 5 elements.

Cardinal Properties of Sets:

(а) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
If A and B are disjoint , then
n(A ∪ B) = n(A) + n(B)

(b) n[A∪B∪C] = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A ∩B ∩ C).