By going through these CBSE Class 11 Maths Notes Chapter 1 Sets Class 11 Notes, students can recall all the concepts quickly.
Sets Notes Class 11 Maths Chapter 1
Set: Any well-defined collection of objects, which are different from each other, and which we can see or think of is called a set.
Members of a set: The objects which belong to a set are called its members or elements.
Representation of a set: There are two ways by which the , sets can be represented :
(a) Tabular form or Roster form : Here, the elements of a
set are actually written down, separated by commas and enclosed * within braces (i.e., curly brackets). Thus,
(i) V, the set of vowels in the English alphabet = {a, e, i, o, u},
(ii) A, the set of odd natural numbers < 10 = {1, 3, 5, 7, 9),
(iii) N, the set of natural numbers = {1, 2, 3,…}.
(b) The set builder form : In this form, we list the property or properties satisfied by the elements of the set. Thus,
(i) M = {2, 3,.5, 7, 11, 13, 17, 191 = {x : x is a prime number < 20).
(ii) A = 16, 7, 8, 9, 10, 11} = {x| ∈ N, 5 < x < 12}, where ∈ stands for ‘belongs to’ and ‘ | ’ stands for ‘such that’.
It may be noted that while writing the set in roster form, an element is not generally repeated. For example, the set of letters of the word ‘SCHOOL’ is (S, C, H, O, L}.
Empty set or null set or void set : A set consisting of no element at all is called the empty set or the null set or the void | set. It is denoted by Φ (Phai). In roster form, it is written as = { }.
Examples : (i) (x : x ∈ N, 1 < x < 2} = Φ.
(ii) {x : x ∈ R, x2 = – 1} = Φ.
Finite Set: A set in which the process of counting of elements surely comes to an end, is called a finite set.
Examples : ii) {x : x ∈ N, x < 500) (ii) Set of all trees on earth.
Infinite Set: A set, in which the process of counting of elements never comes to an end, is called an infinite set. Examples : (i) {x : x ∈ N, x > 50), (ii) {x : x ∈ Z, x < 1}.
Equal Sets : Two sets A and B are said to be equal, if every element of A is in B and every element of B is in A. It is written as A = B.
Examples: (i) {1, 2, 5} = {2, 1, 5} = {5, 1, 2)
(ii) {1, 2, 3, 1} = {1, 2, 3} = {1, 1, 2, 2, 3} etc.
[∵ The repetition of elements in a set is meaningless]
Equivalent Sets : Two finite sets A and B are said to be equivalent, if n(A) = n(B), where n(A) or n(B) is the number of elements in set A or B. It is written as A ↔ B.
Example: If A = {1, 2, 3} and B = {a, b, c}. Then, A ↔ B as n(A) = n(B) = 3.
Whenever A = B, then n(A) = n(B). Thus, equal sets are always equivalent. But, equivalent sets need not be equal.
Disjoint Sets : Two sets are said to be disjoint, if they have no element in common.
Example : A = {1, 3, 5} and B = {2, 4, 6) are disjoint sets.
Subset: If A and B are two sets given in such a way that every element of A is in B, then A is a subset of set B and it is written as A ⊂ B (read as ‘A is contained in B’)
If at least one element of A does not belong to B, then A is not a subset of B. It is written as A ⊄ B.
Example : If A = {1, 2, 3} and B = {3, 2, 4, 1), then A ⊂ B.
Subsets of Set of Real Numbers R :
There are many important subsets of R. Some of them are given below :
(i) The set of natural numbers = N = {1, 2, 3, 4, 5, ….)
(ii) The set of integers Z is
Z = {…., – 3, – 2, – 1, 0, 1, 2, 3, ….}
(iii) The set of rational numbers Q.
Q = {x: x = \(\frac{p}{q}\), p,q ∈ Z and q ≠ 0
(iv) Set of irrational numbers
T = {x : x e R and x ∉ Q} = R – Q.
Members of T are such as √2, √5, √7,…., π, etc.
Here, we observe that
N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, N ⊄ T.
INTERVAL AS SUBSET OF R.
Let a, b ∈ R and a < b.
Open Interval : The set of real numbers {y : a <y < b} is called an open interval and is denoted by (a, b). Here all the points between a and b belong to the open interval (a, b), but a and b do not, belong to this interval.
Closed Interval: Closed interval is defined as {a, b = [x : a ≤ x ≤ b}.
All the points between a and b and the points a and b belong to \a,b).
Closed on the left and open to right: [a, b) = {x:a ≤ x < b}.
All the points between a and b and the point a belong to fa, b) but b does not belong to this interval.
Open on the left and closed to the right:
(a, b] = {x:a < x ≤ b}.
All the points between a and b and the point b belong to (a, 6] but a does not belong to it.
Super Set: If A is subset of B, then we say that B is a super set of A and is written as B ⊃ A.’
Some results on subsets :
- Every set is a subset of itself, i.e.,A⊂A, B⊂B, etc.
- The empty set is a subset of every set, i.e., Φ ⊂ A, Φ ⊂ B, etc.
- If A = B, then A ⊂ B and B ⊂ A.
- If A ⊂ B and B ⊂ A, then A = B.
- If A contains n elements, then A has 2n subsets.
Power Set : The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set.
Proper Subset : If A is a subset of B but A ≠ B, then A is called a proper subset et P and is written as A ⊂ B. Thus, A is a proper subset of B only when every elemént of A is in B and B has at least one extra element than A.
Example: If A {1, 2. 3) and B = (1, 2, 3, 4). Then, A ⊂ B and A ≠ B. Therefore A ⊂ B.
Note : If A is a subset of B and A = B, then A is not a proper subset of B. In such a case, it is denoted as A ⊆ B.
Some results on proper subsets:
- If A ⊂ B and A ≠ B, then A ⊂ B.
- No set is a proper subset of itself.
- Φ is a proper subset of every set except itself.
- Φ has no proper subset.
- A set having n elements has (2n – 1) proper subsets.
Universal Set : If there are some sets under consideration, then there happens to be a set which is a superset of each one of the given sets. Such a set is called the universal set and it is denoted by U or ξ
Venn Diagrams : Most of the relationships between sets can be represented by means of diagrams. Figures representing sets in the form of enclosed region in the plane are called Venn diagrams. In these diagrams, the universal set is usually represented by a rectangular region and its subsets by bounded regions inside this rectangular region.
Venn Diagrams In Different Situations
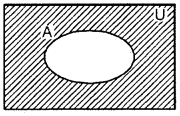
1. A ⊂ U, where U is the universal set.
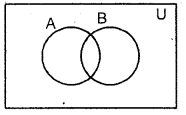
2. Two intersecting subsets of a universal set U.
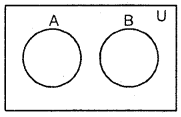
3. Two disjoint subsets of a universal set U.
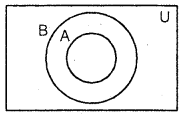
4. A⊂B⊂U, where U is the universal set.
Operation of sets : The main set operations are
- Union of sets
- Intersection of sets
- Difference of sets.
Union of two sets: The union of two
sets A and B, denoted by A u B (read as A union B), is the set of all those elements which are either in A or in B or in both.
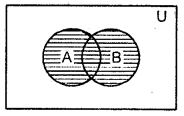
Symbolically:
A∪B = {x:x ∈ A or x ∈ B}.
Example: If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Then,
A ∪ B = {1, 2, 3, 4}∪{2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}.
Some results on union of sets :
- A⊂A⊂B and B⊂A∪B.
- If A ⊂B, then A∪B⊂B.
Intersection of sets : The intersection of two sets A and B, denoted by A ∩ B (read as A intersection B), is the set of all elements common to both A and B.
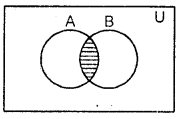
Symbolically:
A ∩ B=[x:x ∈ A and x ∈ B).
Example: If A = (1, 2, 3, 4} and B = {2, 4, 6, 8). Then,
A ∩ B = (l, 2,3, 4}∩{2, 4, 6,8} = {2, 4}.
Disjoint Sets : Two sets A and B are said to be disjoint, if A ∩ B = Φ. ,
If A ∩ B ≠ Φ, then A and B are called overlapping or intersecting sets.
Difference of two sets : The difference of two sets A a.nd B, denoted by A – B (read as A minus B), is the set of all those elements of A which are not in B.
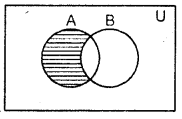
Symbolically :
A-B = {x:x∈A and x ∉ B}.
Example: If A = {1, 2, 3, 4, 6, 12} and B = {1, 2, 4, 8, 16). Then,
A – B = {3, 6,12} and B – A = {8, 16}.
Note : In general A – B ≠ B – A.
Laws of Set Operations:
1. Commutative Laws : For any two sets A and B, we have :
(i) A∪B = B∪A (ii) A ∩ B = B ∩ A.
2. Associative Laws: For any three sets A, B and C, we have :
(i) (A∪B)∪C = A∪(B∪C), {ii) (A∩B)∩C = A∩(B∩C).
3. Distributive Laws : For any three sets A, B and C, we have:
(i) A∪(B∩C) = (A∪B)∩(A∪C).
(ii) A∩(B∪C) = (A∩B)∪(A∩C).
4. Idempotent Laws : If A is any set, then
(i) A∩A = A (ii) A∪A = A,
5. Identity Laws : If A is any subset of a universal set U and Φ is the null set, then
(i) A∩U = A (ii) A∩Φ = Φ
(iii) A∪Φ = A (iv) A∪U = U.
Complement of a set : If U be a Universal set and A is the subset of U, then complement of A with respect to U, denoted by A’ or Ac, is defined as A’ = {x 😡 ∈ U and x ∉ A}, i.e., the complement of A is the set of elements of U which are not the elements of A.
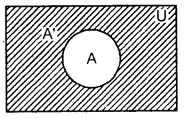
Properties of Complements:
(i) Complement Laws.
(a) A∪A’ = U (b) A∩A’ = Φ
(ii) De Morgan’s Laws.
(a) (A ∪ B)’ = A’∩ B’ (b) (A∩B)’=A’∪B’
(iii) Law of double Complementation (a)(A’)’ = A
(iv) Complement of Φ and ∪
(a) Φ’ = U (b) U’ = Φ.
Cardinal Number : n, the number of elements in a set is called the cardinal number of the set, denoted by n(A).
Example : A = {1, 2, 3, 4, 5} n(A) = 5, since A has 5 elements.
Cardinal Properties of Sets:
(а) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
If A and B are disjoint , then
n(A ∪ B) = n(A) + n(B)
(b) n[A∪B∪C] = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A ∩B ∩ C).