CBSE Class 10

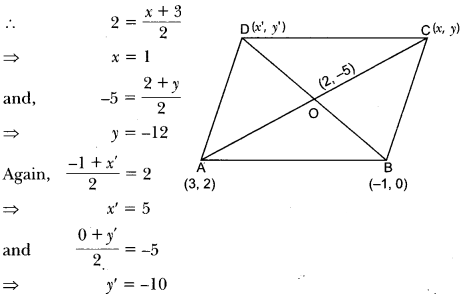
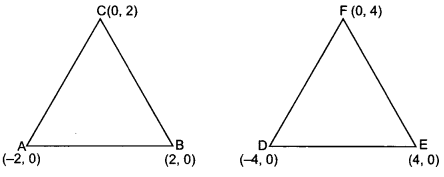
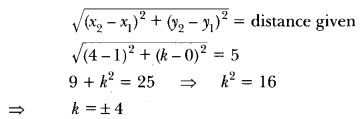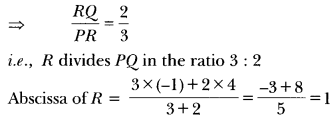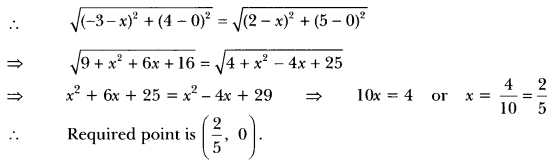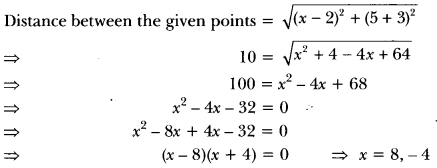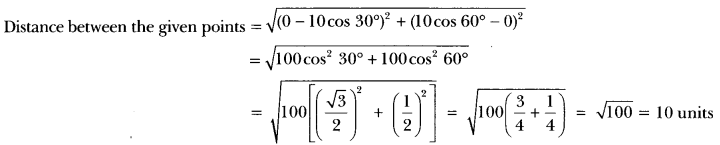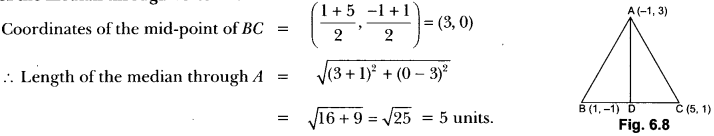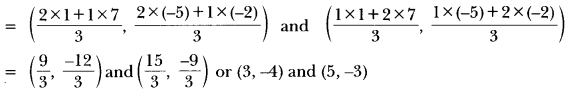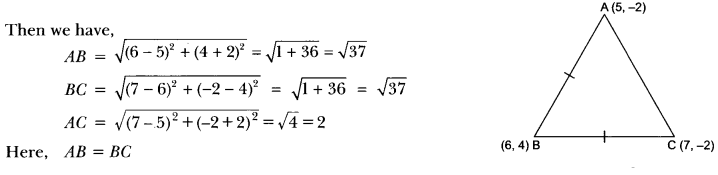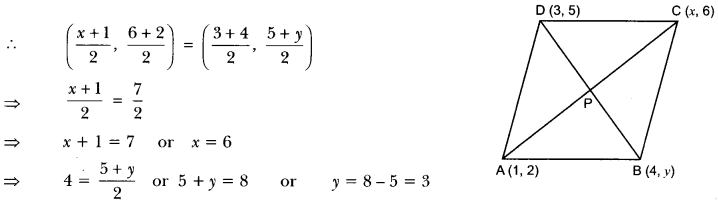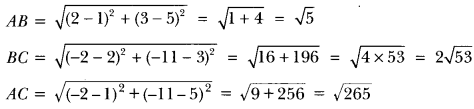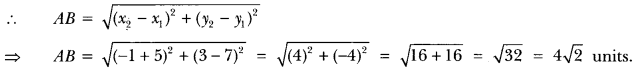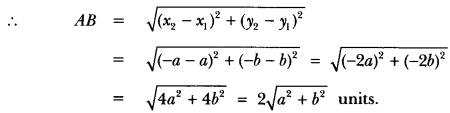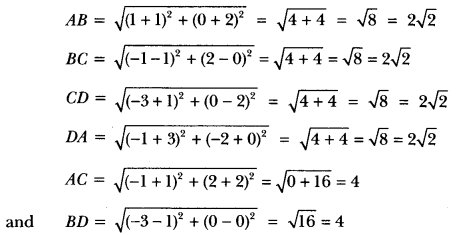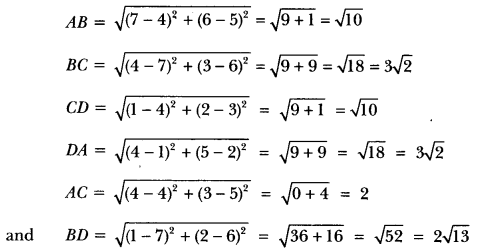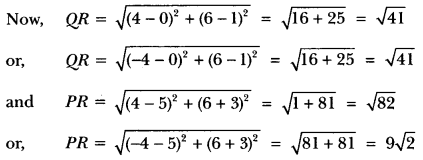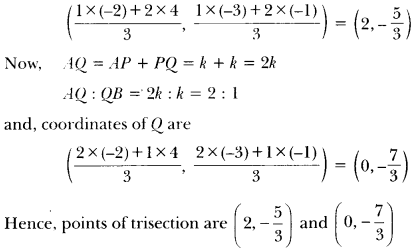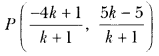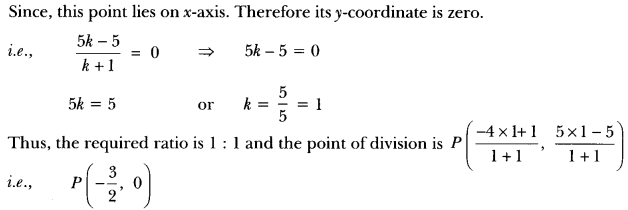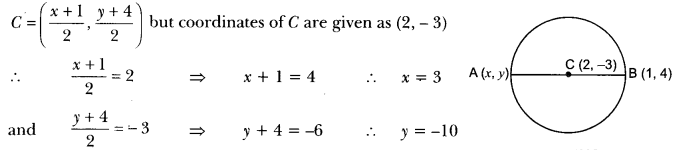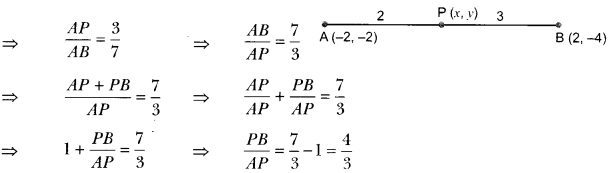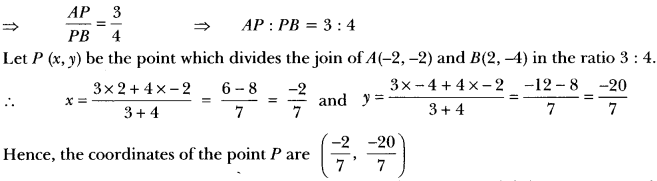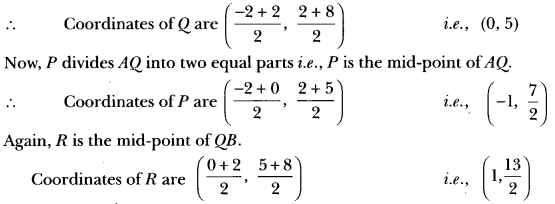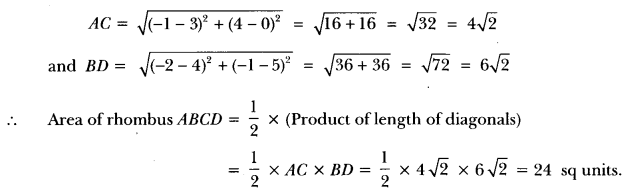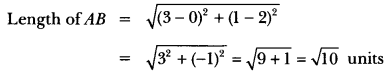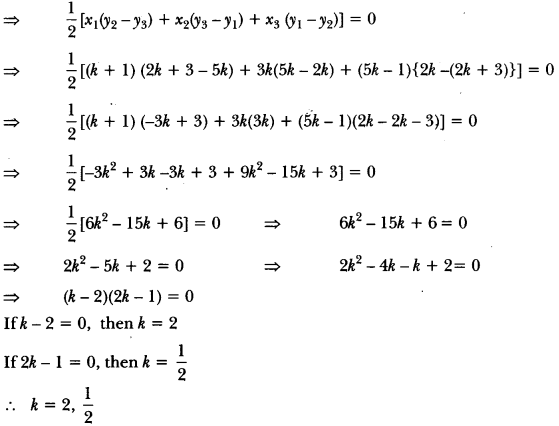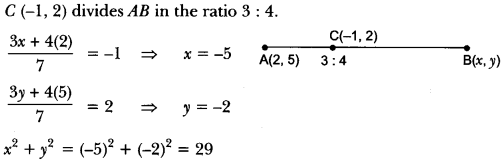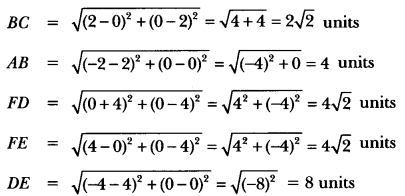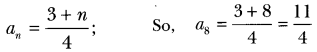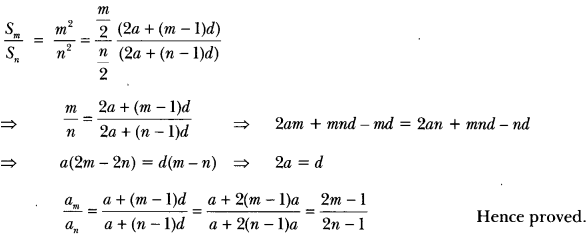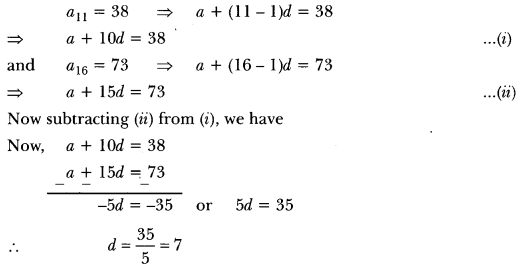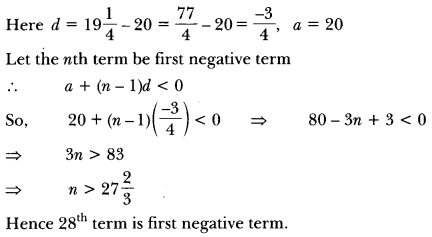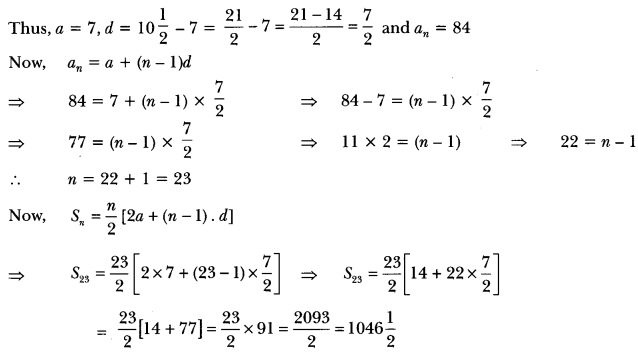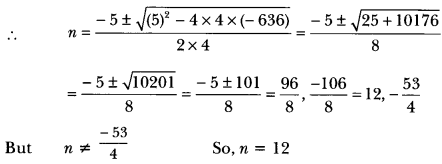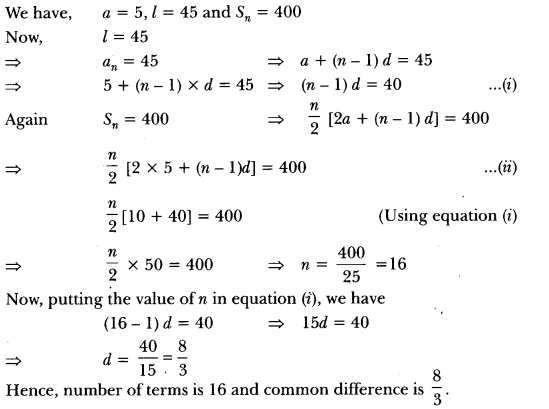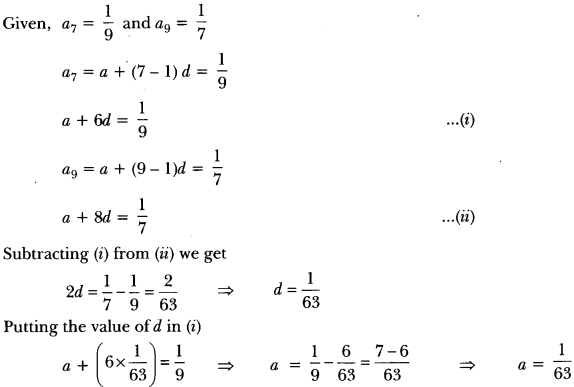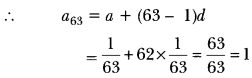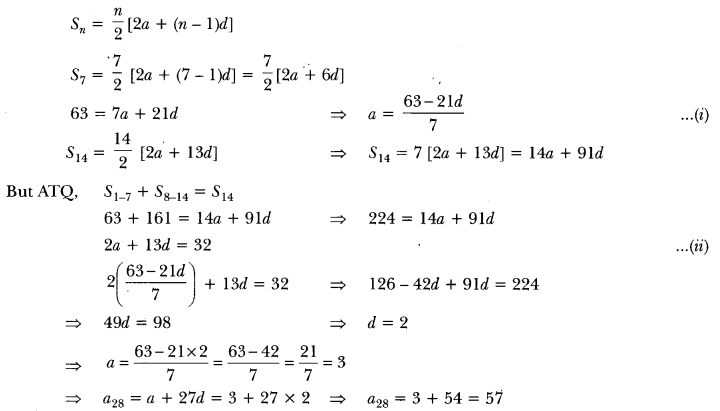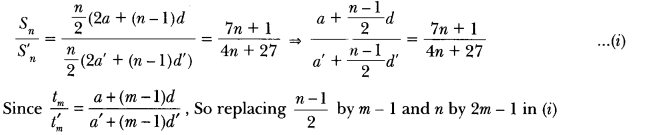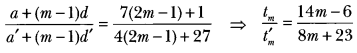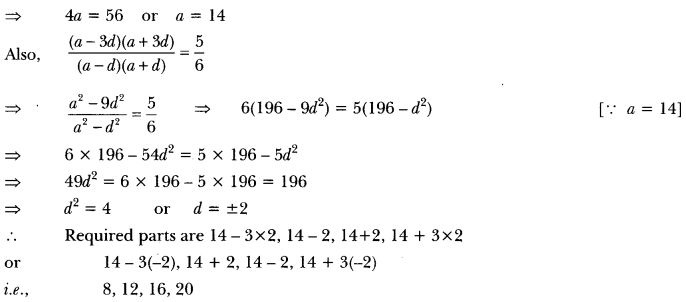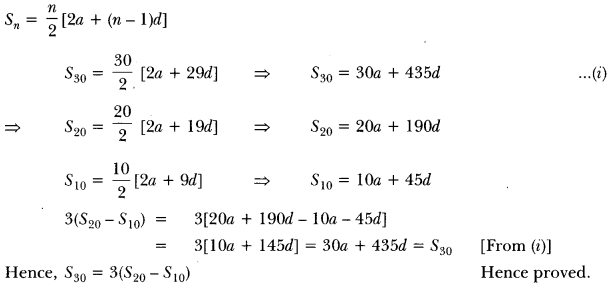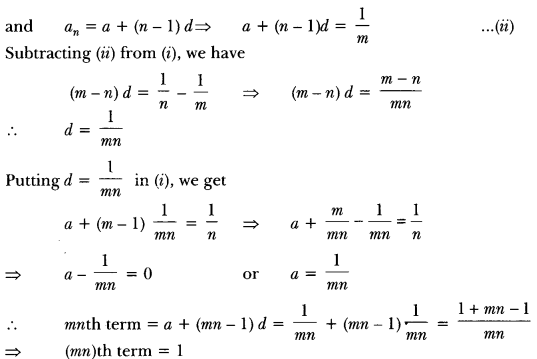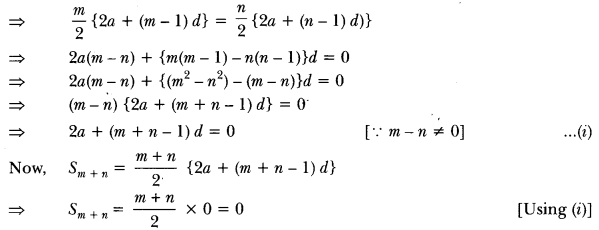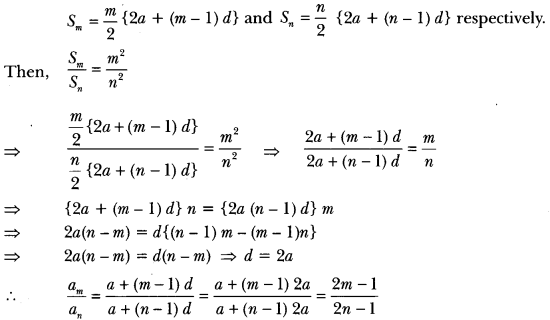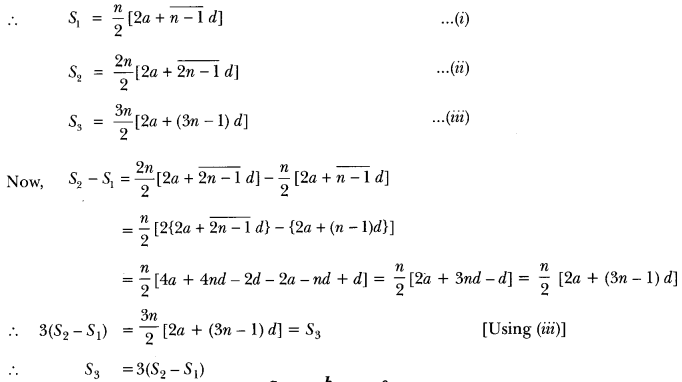Here we are providing Triangles Class 10 Extra Questions Maths Chapter 6 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Triangles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 6 Triangles with Solutions Answers

Triangles Class 10 Extra Questions Very Short Answer Type

Question 1.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Solution:
Since the perimeters and two sides are proportional
∴ The third side is proportional to the corresponding third side.
i.e., The two triangles will be similar by SSS criterion.

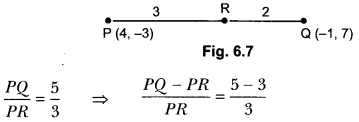
Question 2.
A and B are respectively the points on the sides PQ and PR of a ∆PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm, and PB = 4 cm. Is AB || QR? Give reason.
Solution:

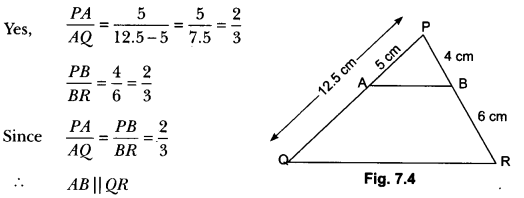
Question 3.
If ∆ABC ~ ∆QRP, \(\frac { ar(∆ABC) }{ ar(∆PQR) } \) = \(\frac{9}{4}\), AB = 18 cm and BC = 15 cm, then find the length of PR.
Solution:

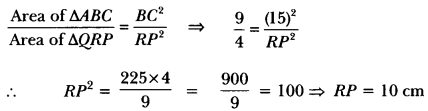
Question 4.
If it is given that ∆ABC ~ ∆PQR with \(\frac{BC}{QR}\) = \(\frac{1}{3}\), then find \(\frac { ar(∆PQR) }{ ar(∆ABC) } \)
Solution:

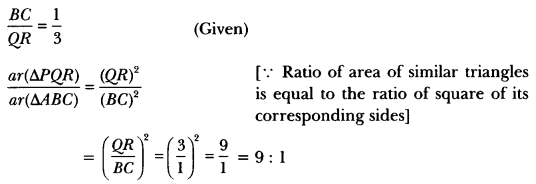
Question 5.
∆DEF ~ ∆ABC, if DE : AB = 2 : 3 and ar(∆DEF) is equal to 44 square units. Find the area (∆ABC).
Solution:

Question 6.
Is the triangle with sides 12 cm, 16 cm and 18 cm a right triangle? Give reason.
Solution:
Here, 12²+ 16² = 144 + 256 = 400 ≠ 18²
∴ The given triangle is not a right triangle.

Triangles Class 10 Extra Questions Short Answer Type 1

Question 1.
In triangles PQR and TSM, ∠P = 55°, ∠Q = 25°, ∠M = 100°, and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Solution:
Şince, ∠R = 180° – (∠P + ∠Q)
= 180° – (55° + 25°) = 100° = ∠M
∠Q = ∠S = 25° (Given)
∆QPR ~ ∆STM
i.e., . ∆QPR is not similar to ∆TSM.

Question 2.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 63°, then the measures of ∠C = 70°. Is it true? Give reason.
Solution:
Since ∆ABC ~ ∆DEF
∴ ∠A = ∠D = 47°
∠B = ∠E = 63°
∴ ∠C = 180° – (∠A + ∠B) = 180° – (47° + 63°) = 70°
∴ Given statement is true.

Question 3.
Let ∆ABC ~ ∆DEF and their areas be respectively 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:

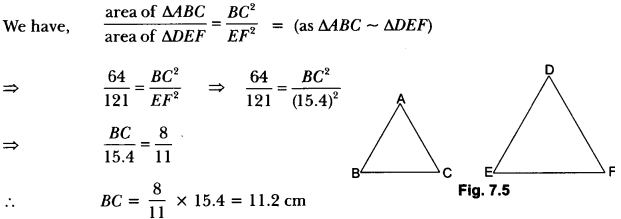
Question 4.
ABC is an isosceles triangle right-angled at C. Prove that AB² = 2AC².
Solution:
∆ABC is right-angled at C.
∴ AB² = AC² + BC² [By Pythagoras theorem]
⇒ AB² = AC² + AC²
[∵ AC = BC]
⇒ AB² = 2AC²

Question 5.
Sides of triangle are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
Solution:
(i) Let a = 7 cm, b = 24 cm and c = 25 cm.
Here, largest side, c = 25 cm
We have, a² + b² = (7)² + (24)² = 49 + 576 = 625 = c² [∵c = 25]
So, the triangle is a right triangle.
Hence, c is the hypotenuse of right triangle.

(ii) Let a = 3 cm, b = 8 cm and c = 6 cm
Here, largest side, b = 8 cm
We have, a² + c² = (3)² + (6)² = 9 + 36 = 45 ≠ b²
So, the triangle is not a right triangle.

Question 6.
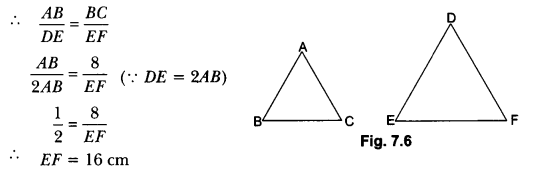
If triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm. Then find the length of EF.
Solution:
∆ABC ~ ∆DEF (Given)

Question 7.
If the ratio of the perimeter of two similar triangles is 4 : 25, then find the ratio of the areas of the similar triangles.
Solution:
∵ Ratio of perimeter of 2 ∆’s = 4 : 25
∵ Ratio of corresponding sides of the two ∆’s = 4 : 25
Now, the ratio of area of 2 ∆’s = Ratio of square of its corresponding sides.
= \(\frac{(4)^{2}}{(25)^{2}}\) = \(\frac{16}{625}\)

Question 8.
In an isosceles ∆ABC, if AC = BC and AB² = 2AC², then find ∠C.
Solution:

AB² = 2AC² (Given)
AB² = AC² + AC²
AB² = AC² + BC² (∵ AC = BC)
Hence AB is the hypotenuse and ∆ABC is a right angle A.
So, ∠C = 90°

Question 9.
The length of the diagonals of a rhombus are 16 cm and 12 cm. Find the length of side of the rhombus.

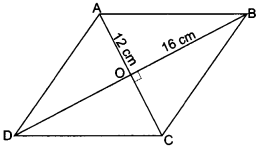
Solution:
∵ The diagonals of rhombus bisect each other at 90°.
∴ In the right angle ∆BOC
BO = 8 cm
CO = 6 cm
∴ By Pythagoras Theorem
BC² = BO² + CO² = 64 + 36
BC² = 100
BC = 10 cm

Question 10.
A man goes 24 m towards West and then 10 m towards North. How far is he from the starting point?
Solution:

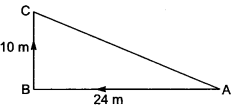
By Pythagoras Theorem
AC² = AB² + BC² = (24)² + (10)²
AC² = 676
AC = 26 m
∴ The man is 26 m away from the starting point.

Question 11.
∆ABC ~ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, what is the perimeter of ∆ABC?
Solution:
Since ∆ABC ~ ∆DEF.

Question 12.
∆ABC ~ ∆PQR; if area of ∆ABC = 81 cm², area of ∆PQR = 169 cm² and AC = 7.2 cm, find the length of PR.
Solution:
Since ∆ABC ~ ∆PQR

Triangles Class 10 Extra Questions Short Answer Type 2

Question 1.
In Fig. 7.10, DE || BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x.
Solution:

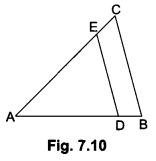
In ∆ABC, we have
DE || BC,
∴ \(\frac{A D}{D B}\) = \(\frac{A E}{E C}\) [By Basic Proportionality Theorem]
⇒ \(\frac{x}{x-2}\) = \(\frac{x+2}{x-1}\)
⇒ x(x – 1) = (x – 2) (x + 2)
⇒ x² – x = x² – 4
⇒ x = 4

Question 2.
E and F are points on the sides PQ and PR respectively of a ∆PQR. Show that EF ||QR if PQ = 1.28 cm, PR= 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
Solution:

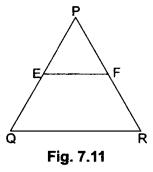
We have, PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm
Now, EQ = PQ-PE = 1.28 – 0.18 = 1.10 cm and
FR = PR – PF = 2.56 – 0.36 = 2.20 cm

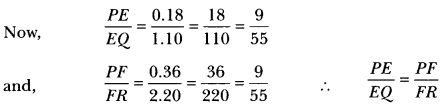
Therefore, EF || QR [By the converse of Basic Proportionality Theorem]

Question 3.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Let AB be a vertical pole of length 6m and BC be its shadow and DE be tower and EF be its shadow. Join AC and DF.
Now, in ∆ABC and ∆DEF, we have

h = 42 Hence, height of tower, DE = 42m

Question 4.
In Fig. 7.13, if LM || CB and LN || CD, prove that \(\frac{A M}{A B}=\frac{A N}{A D}\)
Solution:

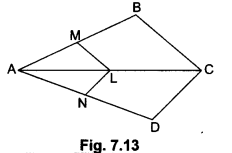
Firstly, in ∆ABC, we have
LM || CB (Given)
Therefore, by Basic Proportionality Theorem, we have

Question 5.
In Fig. 7.14, DE || OQ and DF || OR Show that EF || QR.
Solution:
In ΔPOQ, we have
DE || OQ (Given)

[Applying the converse of Basic Proportionality Theorem in ∆PQR]

Question 6.
Using converse of Basic Proportionality Theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution:

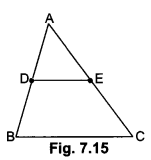
Given: ∆ABC in which D and E are the mid-points of sides AB and AC respectively.
To prove: DE || BC
Proof: Since D and E are the mid-points of AB and AC respectively
∴ AD = DB and AE = EC

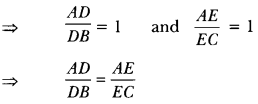
DB EC Therefore, DE || BC (By the converse of Basic Proportionality Theorem)

Question 7.
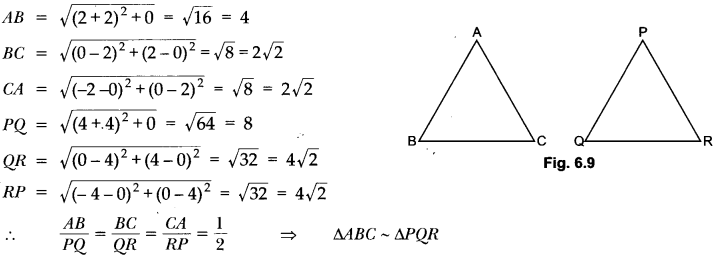
State which pairs of triangles in the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form.

Solution:
(i) In ∆ABC and ∆QRP, we have


∆NML is not similar to ∆PQR.

Question 8.
In Fig. 7.17, \(\frac{A O}{O C}\) = \(\frac{B O}{O D}\) = \(\frac{1}{2}\) and AB = 5cm. Find the value of DC.
Solution:

⇒ DC = 10 cm.

Question 9.
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:

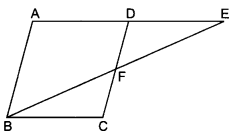
In ∆ABE and ∆CFB, we have
∠AEB = ∠CBF (Alternate angles)
∠A = ∠C (Opposite angles of a parallelogram)
∴ ∆ABE ~ ∆CFB (By AA criterion of similarity)

Question 10.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:

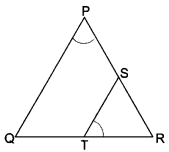
In ∆RPQ and ∆RTS, we have
∠RPQ = ∠RTS (Given)
∠PRQ = ∠TRS = ∠R (Common)
∴ ∆RPQ ~ ∆RTS (By AA criterion of similarity)

Question 11.
In Fig. 7.20, ABC and AMP are two right triangles right-angled at B and M respectively. Prove that:
(i) ∆ABC ~ ∆AMP
(ii) \(\frac{C A}{P A}\) = \(\frac{B C}{M P}\)
Solution:

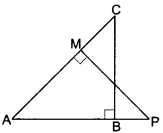
(i) In ∆ABC and ∆AMP, we have
∠ABC = ∠AMP = 90° (Given)
And, ∠BAC = ∠MAP (Common angle)
∴ ∆ABC ~ ∆AMP (By AA criterion of similarity)

(ii) As ∆ABC ~ ∆AMP (Proved above)
∴ \(\frac{C A}{P A}\) = \(\frac{B C}{M P}\) (Sides of similar triangles are proportional)

Question 12.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Solution:

Question 13.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:

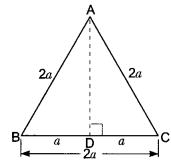
Let ABC be an equilateral triangle of side 2a units.
We draw AD ⊥ BC. Then D is the mid-point of BC.
⇒ \(\frac{B C}{2}\) = \(\frac{2 a}{2}\) = a
Now, ABD is a right triangle right-angled at D.
⇒ AB² = AD² + BD² [By Pythagoras Theorem]
⇒ (2a)² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
⇒ AD = √3a
Hence, each altitude = √3a unit.

Question 14.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1 \(\frac{1}{2}\) hours?
Solution:

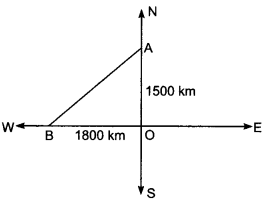
Let the first aeroplane starts from O and goes upto A towards north where

(Distance = Speed × Time)
Again let second aeroplane starts from O at the same time and goes upto B towards west where
OB = 1200 × \(\frac{3}{2}\) = 1800 km
Now, we have to find AB.
In right angled ∆ABO, we have
AB² = OA² + OB² [By using Pythagoras Theorem]
⇒ AB² = (1500)² + (1800)²
⇒ AB² = 2250000 + 3240000
⇒ AB² = 5490000
∴ AB = 100 √549 = 100 × 23.4307 = 2343.07 km.

Question 15.
In the given Fig. 7.24, ∆ABC and ADBC are on the same base BC. If AD intersects BC at 0. Prove
that \(\frac { ar(∆ABC) }{ ar(∆DBC) }\) = \(\frac{AO}{DO}\)
Solution:
Given: ∆ABC and ∆DBC are on the same base BC and AD intersects BC at O.

Question 16.
In Fig. 7.25, AB || PQ || CD , AB = x units, CD = y units and PQ = z units. Prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\).
Solution:

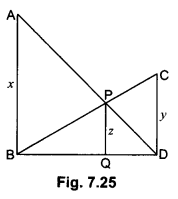
In ∆ADB and ∆PDQ,
Since AB || PQ
∠ABQ = ∠PQD (Corresponding ∠’s)
∠ADB = ∠PDQ (Common)
By AA-Similarity
ΔADB ~ ΔPDQ

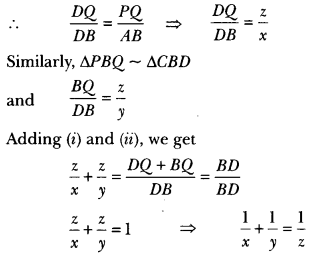
Question 17.
In Fig. 7.26, if ∆ABC ~ ∆DEF and their sides are of lengths (in cm) as marked along with them, then find the lengths of the sides of each triangle.
Solution:
∆ABC ~ ∆DEF (Given)

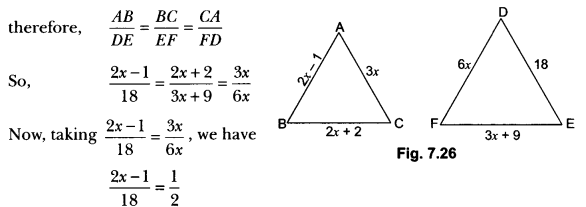
⇒ 4x – 2 = 18
⇒ x = 5
∴ AB = 2 × 5 – 1 = 9, BC = 2 × 5 + 2 = 12
CA = 3 × 5 = 15, DE = 18, EF = 3 × 5 + 9 = 24
and FD = 6 × 5 = 30
Hence, AB = 9 cm, BC = 12 cm, CA = 15 cm
DE = 18 cm, EF = 24 cm, FD = 30 cm

Question 18.
In ΔABC, it is given that \(\frac{A B}{A C}\) = \(\frac{B D}{D C}\) . If ∠B = 70° and ∠C = 50° then find ∠BAD.
Solution:

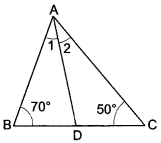
In ∆ABC
∵ ∠A + ∠B + 2C = 180° (Angle sum property)
∠A + 70° + 50° = 180°
⇒ ∠A = 180° – 120°
⇒ ∠A = 60°
∵ \(\frac{A B}{A C}\) = \(\frac{B D}{D C}\) (Given)
∴ ∠1 = ∠2
[Because if a line through one vertex of a triangle divides the opposite sides in the ratio of the other two sides, then the line bisects the angle at the vertex.]
But ∠1 + ∠2 = 60° …(ii)
From (i) and (ii) we get,
2∠1 = 60°
⇒ ∠1 = \(\frac{60°}{2}\) = 30°
Hence, ∠BAD = 30°

Question 19.
If the diagonals of a quadrilateral divide each other proportionally, prove that it is a trapezium.
Solution:

AB || DC
⇒ In quad ABCD, AB || DC
⇒ ABCD is a trapezium.

Question 20.
In the given Fig. 7.29, \(\frac{P S}{S Q}\) = \(\frac{P T}{T R}\) and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
Solution:

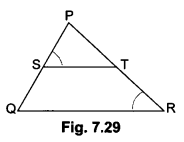
Given: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\) and ∠PST = ∠PRQ
To Prove: PQR is isosceles triangle.
Proof: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\)
By converse of BPT we get
ST || QR
∴ ∠PST = ∠PQR (Corresponding angles) ….(i)
But, ∠PST = ∠PRQ (Given) ….(ii)
From equation (i) and (ii)
∠PQR = ∠PRQ
⇒ PR = PQ
So, ∆PQR is an isosceles triangle.

Question 21.
The diagonals of a trapezium ABCD in which AB || DC, intersect at O. If AB = 2CD, then find the ratio of areas of triangles AOB and COD.
Solution:

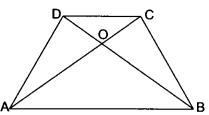
In ∆AOB and ∆COD
∠COD = ∠AOB (Vertically opposite angles)
∠CAB = ∠DCA (Alternate angles)
∆AOB ~ ∆COD (By AA-Similarity)
By area theorem

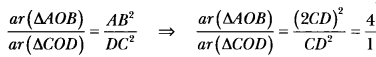
Hence, ar(∆AOB) : ar(∆COD) = 4 : 1.

Question 22.
In the given Fig. 7.31, find the value of x in terms of a, b and c.
Solution:
In ∆LMK and ∆PNK
We have, ∠M = ∠N = 50° and ∠K = ∠K (Common)
∴ ∆LMK ~ ∆PNK (AA – Similarity)

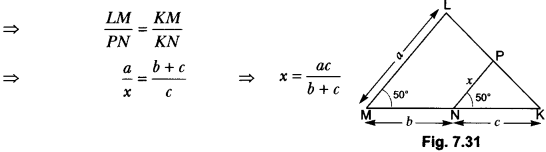
Question 23.
In the given Fig. 7.32, CD || LA and DE || AC. Find the length of CL, if BE = 4 cm and EC = 2 cm.
Solution:

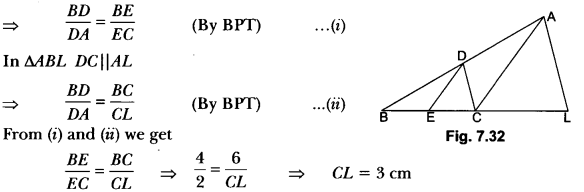
Question 24.
In the given Fig. 7.33, AB = AC. E is a point on CB produced. If AD is perpendicular to BC and EF perpendicular to AC, prove that ∆ABD is similar to ∆ECF.
Solution:

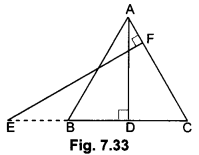
AB = AC (Given)
⇒ ∠ABC = ∠ACB (Equal sides have equal opposite angles)
Now, in ∆ABD and ∆ECF
∠ABD = ∠ECF (Proved above)
∠ADB = ∠EFC (Each 90°)
So, ∆ABD ~ ∆ECF (AA – Similarity)

Triangles Class 10 Extra Questions Long Answer Type

Question 1.
Using Basic Proportionality Theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Solution:

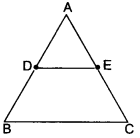
Given: A ∆ABC in which D is the mid-point of AB and DE is drawn parallel to BC, which meets AC at E.
To prove: AE = EC
Proof: In ∆ABC, DE || BC
∴ By Basic Proportionality Theorem, we have
\(\frac{A D}{D B}\) = \(\frac{A E}{E C}\) …(i)
Now, since D is the mid-point of AB
⇒ AD = BD …(ii)
From (i) and (ii), we have
\(\frac{A D}{D B}\) = \(\frac{A E}{E C}\)
⇒ 1 = \(\frac{A E}{E C}\)
Hence, E is the mid-point of AC.

Question 2.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{A O}{B O}\) = \(\frac{C O}{D O}\).
Solution:
Given: ABCD is a trapezium, in which AB || DC and its diagonals intersect each other at point O.

Question 3.
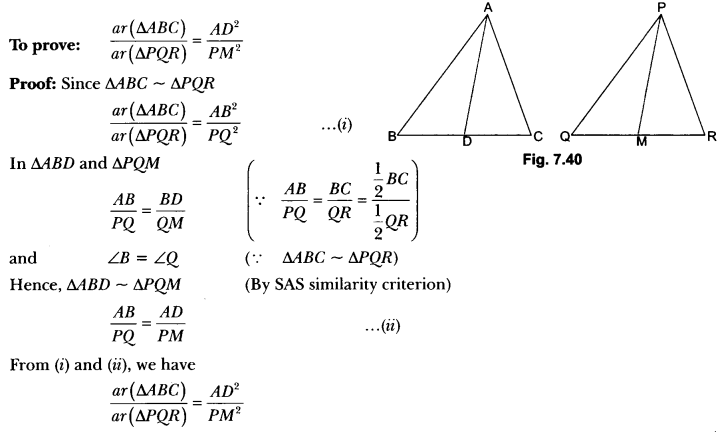
If AD and PM are medians of triangles ABC and PQR respectively, where ∆ABC ~ ∆PQR, prove that \(\frac{A B}{P Q}\) = \(\frac{A D}{P M}\)
Solution:
In ΔABD and ΔPQM we have
∠B = ∠Q (∵ ∆ABC ~ ∆PQR) …(i)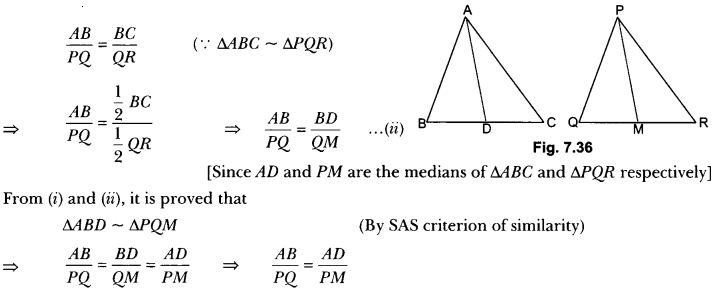

Question 4.
In Fig. 7.37, ABCD is a trapezium with AB || DC. If ∆AED is similar to ΔBEC, prove that AD = BC.
Solution:
In ∆EDC and ∆EBA we have
∠1 = ∠2 [Alternate angles]
∠3 = ∠4 [Alternate angles]
∠CED = ∠AEB [Vertically opposite angles]
∴ ∆EDC ~ ∆EBA [By AA criterion of similarity]

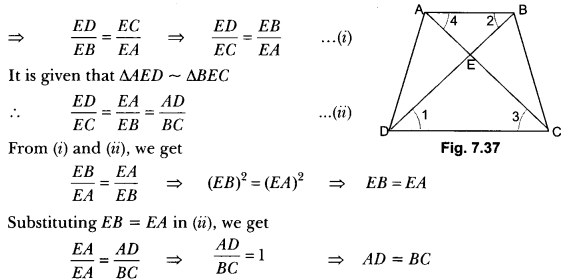
Question 5.
Prove that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.
Solution:

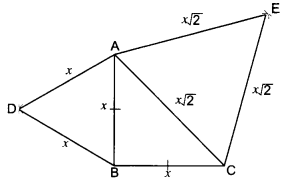
Given: A ∆ABC in which ∠ABC = 90° and AB = BC.
∆ABD and ΔCAE are equilateral triangles.
To Prove: ar(∆ABD) = \(\frac {1}{2}\) × ar(∆CAE)
Proof: Let AB = BC = x units.
∴ hyp. CA = √x² + √x² = x√2 units.
Each of the ABD and ∆CAE being equilateral has each angle equal to 60°.
∴ ∆АВD ~ ∆CAE
But, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Question 6.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:

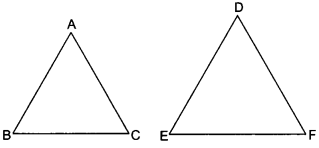
Given: Two triangles ABC and DEF, such that
∆ABC ~ ∆DEF and area (∆ABC) = area (∆DEF)
To prove: ∆ABC ≅ ∆DEF
Proof: ∆ABC ~ ∆DEF
⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

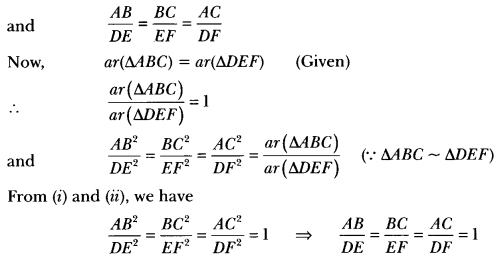
AB = DE, BC = EF, AC = DF
∆ABC ≅ ∆DEF (By SSS criterion of congruency)

Question 7.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
Let ∆ABC and ∆PQR be two similar triangles. AD and PM are the medians of ∆ABC and ∆PQR respectively.

Question 8.
In Fig. 7.41,0 is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
Solution:

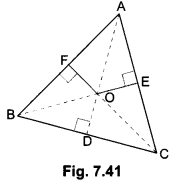
Join OA, OB and OC.
(i) In right ∆’s OFA, ODB and OEC, we have
OA² = AF² + OF² …(i)
OB² = BD² + OD² …(ii)
and C² = CE² + OE²
Adding (i), (ii) and (iii), we have
⇒ 0A² + OB² + OC² = AF² + BD² + CE² + OF² + OD² + OE²
⇒ 0A² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

(ii) We have, OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
⇒ (OA² – OE²) + (OB² – OF²) – (OC² – OD²) = AF² + BD² + CE²
⇒ AE² + CD² + BF² = AP² + BD² + CE²
[Using Pythagoras Theorem in ∆AOE, ∆BOF and ∆COD]

Question 9.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see Fig. 7.42). Prove that 2AB² = 2AC² + BC²
Solution:

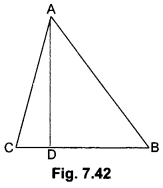
We have, DB = 3CD
Now,
BC = BD + CD
⇒ BC = 3CD + CD = 4CD (Given DB = 3CD)
∴ CD = \(\frac{1}{4}\) BC
and DB = 3CD = \(\frac{1}{4}\)BC
Now, in right-angled triangle ABD using Pythagoras Theorem we have
AB² = AD² + DB² …(i)
Again, in right-angled triangle ∆ADC, we have
AC² = AD² + CD² …(ii)
Subtracting (ii) from (i), we have
AB² – AC² = DB² – CD²

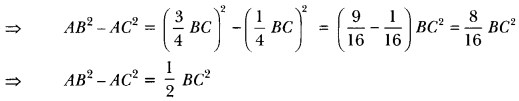
∴ 2AB² – 2AC² = BC²
⇒ 2AB² = 2AC² + BC²

Question 10.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:

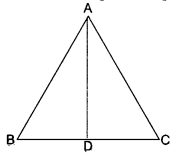
Let ABC be an equilateral triangle and let AD ⊥ BC.
∴ BD = DC
Now, in right-angled triangle ADB, we have
AB² = AD² + BD² [Using Pythagoras Theorem]

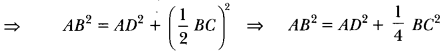
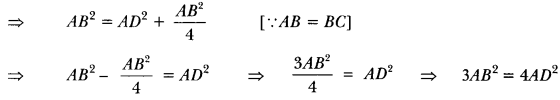
Question 11.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7.44 DE || BC and BD = CE. Prove that ∆ABC is an isosceles triangle.

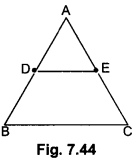
Solution:
Given: A triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively.

⇒ AB = AC (As DB = EC)
∴ ∆ABC is an isosceles triangle.

Question 12.
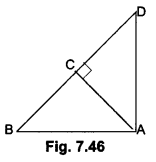
In Fig. 7.46, ABD is a triangle right-angled at A and AC ⊥ BD Show that
(i) AB² = BC. BD
(ii) AD² = BD.CD
(iii) AC² = BC.DC
Solution:
Given: ABD is a triangle right-angled at A and AC ⊥ BD.

To prove: (i) AB² = BC .BD
(ii) AD² = BD.CD
(iii) AC² = BC . DC
Proof: (i) In ∆ACB and ∆DAB, we have
∠ACB = ∠DAB = 90°
∠ABC = ∠DBA = ∠B [Common]
∴ ∆ACB ~ ∆DAB [By AA criterion of similarity]
\(\frac{BC}{AB}=\frac{AB}{DB}\)
⇒ AB² = BC.BD

(ii) In ∆ACD and ∆BAD, we have
∠ACD = ∠BAD = 90°
∠CDA = ∠BDA = ∠D [Common]
∴ ∆ACD ~ ∆BAD [By AA criterion of similarity]
\(\frac{AD}{BD}=\frac{CD}{AD}\)
⇒ AD² = BD.CD

(iii) We have ∆ACB – ∆DAB
⇒ ∆ВСА ~ ∆ВAD …(i)
and ∆ACD ~ ∆BAD …(ii)
From (i) and (ii), we have
∆ВСА ~ ∆АСD
\(\frac{B C}{A C}=\frac{A C}{D C}\)
AC² = BC . DC

Question 13.
Prove that ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. Using the above result do the following: Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:
Given: Two triangles ABC and PQR such that ∆ABC ~ ∆PQR


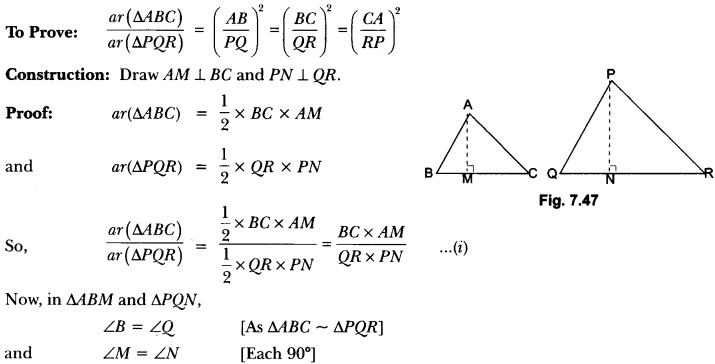
Second Part:

In ∆AOB and ∆COD we have
∠AOB = ∠COD (Vertically opposite angles) and
∠OAB = ∠OCD (Alternate angles)
∆AOB ~ ∆COD (By AA criterion of similarity]

Hence, the ratio of areas of ∆AOB and ∆COD 4 : 1.

Question 14.
Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Using the above, do the following:
Prove that, in a ∆ABC if AD is perpendicular to BC, then AB² + CD² = AC² + BD².
Solution:

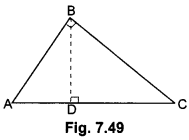
Given: A right triangle ABC right-angled at B.
To Prove: AC² = AB² + BC²
Construction: Draw BD ⊥ AC
Proof: In ∆ADB and ∆ABC
∠A = ∠A (Common)
∠ADB = ∠ABC (Both 90°)
∴ ∆ADB ~ ∆ABC (AA similarity criterion)

Adding (i) and (ii), we get
AD. AC + CD . AC = AB² + BC²
or, AC (AD + CD) = AB² + BC²
or, AC . AC = AB² + BC²
or, AC² = AB² +BC²

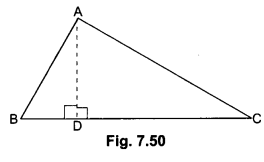
Second Part:
In Fig. 7.50, As AD ⊥ BC
Therefore, ∠ADB = ∠ADC = 90°
By Pythagoras Theorem, we have
AB² = AD² + BD² …..(i)
AC² = AD² + DC² …..(ii)
Subtracting (ii) from (i)
AB² – AC² = AD² + BD² – (AD² + DC²)
⇒ AB² – AC² = BD² – DC² = AB² + DC² = BD² + AC²

Question 15.
In a triangle, if the square on one side is equal to the sum of the squares on the other two sides, prove that the angle opposite to the first side is a right angle. Use the above theorem to find the measure of ∠PKR in Fig. 7.51.

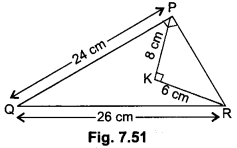
Solution:
Given: A triangle ABC in which AC² = AB² + BC²
To Prove: ∠B = 90°.
Construction: We construct a ∆PQR right-angled at Q such that PQ = AB and QR = BC
Proof: Now, from ∆PQR, we have,

Question 16.
ABC is a triangle in which AB = AC and D is a point on AC such that BC² = AC × CD. Prove that BD = BC.
Solution:
Given: ∆ABC in which AB = AC and D is a point on the side AC such that BC² = AC × CD
To prove: BD = BC
Construction: Join BD
Proof: We have,

Question 17.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
Let ABCD be a square and ABCE and ∆ACF have been drawn on side BC and the diagonal AC respectively.

Question 18.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
Solution:

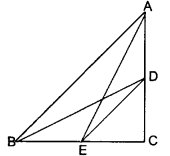
In right angled ΔACE and ΔDCB, we have
AE² = AC² + CE² (Pythagoras Theorem) …(i)
and BD² = DC² + BC²… (ii)
Adding (i) and (ii), we have
AE² + BD² = AC² + CE² + DC² + BC²
AE² + BD² = (AC² + BC²) + (DC² + CE²)
AE² + BD² = AB² + DE²
[∵ AC² + BC² = AB² in right-angled triangle ABC and DC² + EC² = DE² in right-angled triangle CDE.]

Triangles Class 10 Extra Questions HOTS

Question 1.
In Fig. 7.57, ΔFEC ≅ ΔGDB and ∠1 = ∠2. Prove that ΔADE ~ ∆ABC.
Solution:
Since ΔFEC ≅ ΔGDB

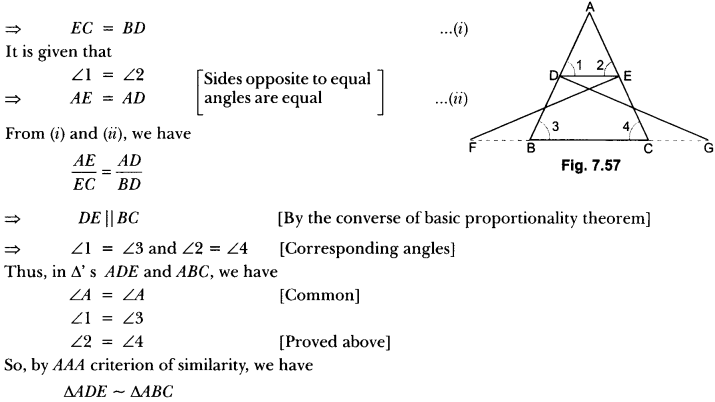
Question 2.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution:
Given: In ∆ABC and ∆PQR, AD and PM are their medians respectively

To prove: ∆ABC ~ ∆PQR
Construction: Produce AD to E such that AD = DE and produce PM to N such that PM = MN. Join BE, CE, QN, RN.
Proof: Quadrilateral ABEC and PQNR are ||^gm because their diagonals bisect each other at D and M respectively.
⇒ BE = AC and QN = PR


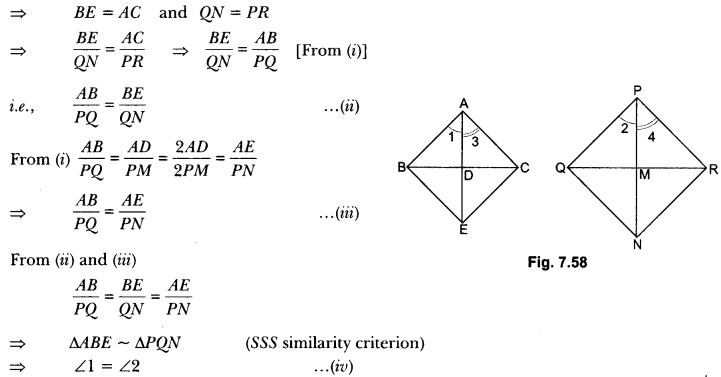
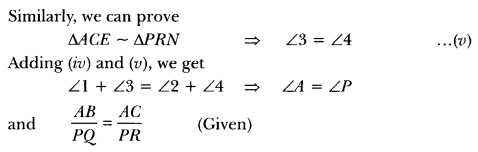
∆ABC ~ ∆PQR (By SAS criterion of similarity)

Question 3.
In Fig. 7.59, P is the mid-point of BC and Q is the mid-point of AP. If BQ when produced meets AC at R, prove that RA = \(\frac{1}{3}\) CA.
Solution:

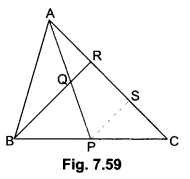
Given: In ∆ABC, P is the mid-point of BC, Q is the mid-point of AP such that BQ produced meets AC at R.
To prove: RA = \(\frac{1}{3}\) CA
Construction: Draw PS || BR, meeting AC at S.
Proof: In ABCR, P is the mid-point of BC and PS || BR.
∴ S is the mid-point of CR.
⇒ CS = SR ….(i)
In ∆APS, Q is the mid-point of AP and QR ||PS
∴ R is the mid-point of AS.
∴ AR = RS …(ii)
From (i) and (ii), we get
AR = RS = SC
⇒ AC = AR + RS + SC = 3 AR
⇒ AR = \(\frac{1}{3}\)AC = \(\frac{1}{3}\)CA

Question 4.
In Fig. 7.60, ABC and DBC are two triangles on the same base BC. If ar(∆ABC) AO AD intersects BC at O, show that \(\frac { ar(∆ABC) }{ ar(∆DBC) }\) = \(\frac{AO}{DO}\)

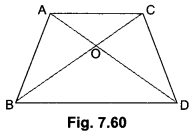
Solution:
Given: Two triangles ∆ABC and ADBC which stand on the same base but on opposite sides of BC.

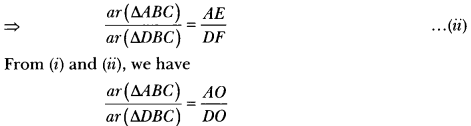
Question 5.
Two poles of height a metres and b metres are p metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given \(\frac{a b}{a+b}\) metres.
Solution:
Let AB and CD be two poles of height a and b metres respectively such that the poles are p metres
apart i.e., AC = p metres.
Suppose the lines AD and BC meet at O such that OL = h metres.
Let CL = x and LA = y. Then, x + y = p.
In ∆ABC and ALOC, we have
∠CAB = ∠CLO [Each equal to 90°)
∠C = ∠C [Common]
∴ ∆ABC ~ ∆LOC [By AA criterion of similarity]

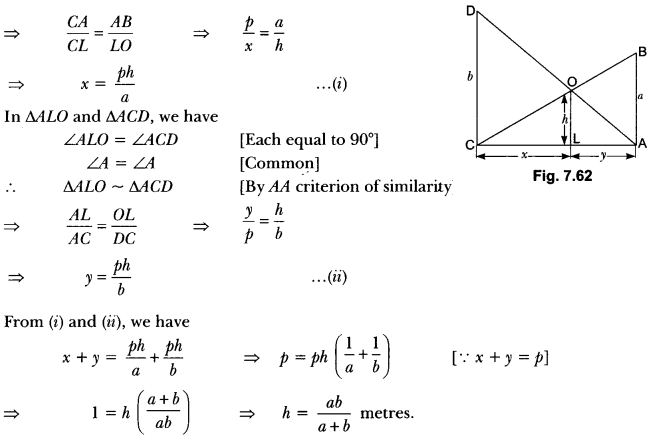
Hence, the height of the intersection of the lines joining the top of each pole to the foot of the opposite pole is \(\frac{a b}{a+b}\) metres.

Question 6.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\) BC. Prove that 9AD² = 7AB².
Solution:

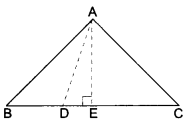
Given: An equilateral triangle ABC and D be a point on BC such that
BD = \(\frac{1}{3}\) BC.
To Prove: 9AD² = 7AB²
Construction: Draw AE ⊥ BC. Join AD.
DE Proof: ∆ABC is an equilateral triangle and AE ⊥ BC
BE = EC
Thus, we have
BD = \(\frac{1}{3}\) BC and DC = \(\frac{2}{3}\) BC and BE = EC = \(\frac{1}{2\) BC
In ∆AEB
AE² + BE² = AB² [Using Pythagoras Theorem]
AE² = AB² – BE²
AD² – DE² = AB² – BE² [∵ In ∆AED, AD² = AE² + DE²]
AD² = AB² – BE² + DE²

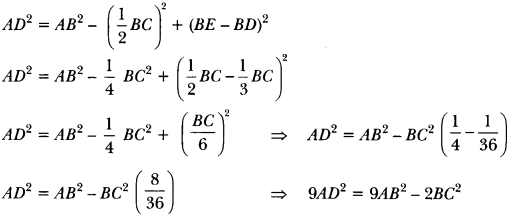
9AD² = 9AB² – 2AB² [∵ AB = BC]
9AD² = 7AB²

Question 7.
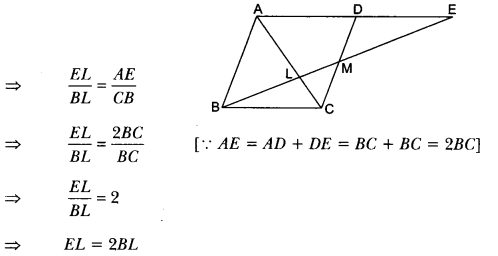
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced to E. Prove that EL = 2BL.
Solution:
In ∆BMC and ∆EMD, we have
MC = MD [∵ M is the mid-point of CD]
∠CMB = ∠DME [Vertically opposite angles]
and ∠MBC = ∠MED [Alternate angles]
So, by AAS criterion of congruence, we have
∆BMC ≅ ∆EMD
⇒ BC = DE [CPCT]
Also, BC = AD [∵ ABCD is a parallelogram]
Now, in ∆AEL and ∆CBL, we have
∠ALE = ∠CLB [Vertically opposite angles]
∠EAL = ∠BCL [Alternate angles]
So, by AA criterion of similarity of triangles, we have
∆AEL ~ ∆CBL

Here we are providing Coordinate Geometry Class 10 Extra Questions Maths Chapter 7 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Coordinate Geometry with Answers Solutions

Extra Questions for Class 10 Maths Chapter 7 Coordinate Geometry with Solutions Answers

Coordinate Geometry Class 10 Extra Questions Very Short Answer Type

Answer the following questions in one word, one sentence or as per the exact requirement of the question.

Question 1.
What is the area of the triangle formed by the points 0 (0, 0), A (-3, 0) and B (5, 0)?
Solution:
Area of ∆OAB = \(\frac{1}{2}\) [0(0 – 1) – 3(0 – 0) + 5(0 – 0)] = 0
⇒ Given points are collinear

Question 2.
If the centroid of triangle formed by points P (a, b), Q (b, c) and R (c, a) is at the origin, what is the value of a + b + c?
Solution:

Question 3.
AOBC is a rectangle whose three vertices are A (0, 3), 0 (0, 0) and B (5, 0). Find the length of its diagonal.
Solution:

Question 4.
Find the value of a, so that the point (3, a) lie on the line 2x – 3y = 5.
Solution:
Since (3, a) lies on the line 2x – 3y = 5
Then 2(3) – 3(a) = 5
– 3a = 5 – 6
– 3a = -1
⇒ a = \(\frac{1}{3}\)

Question 5.
Find distance between the points (0, 5) and (-5, 0).
Solution:
Here x₁ = 0, y₁ = 5, x₂ = -5 and y₂ = 0)

Question 6.
Find the distance of the point (-6,8) from the origin.
Solution:
Here x₁ = -6, y₁ = 8
x₂ = 0, y₂ = 0

Question 7.
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Solution:
Using distance formula

Question 8.
If the points A (1, 2), B (0, 0) and C (a, b) are collinear, then what is the relation between a and b?
Solution:
Points A, B and C are collinear
⇒ 1(0 – b) + 0 (b – 2) + a(2 – 0) = 0
⇒ -b + 2a = 0 or 2a = b

Question 9.
Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (-1, 6).
Solution:
In Fig. 6.6, let the point P(-1, 6) divides the line joining A(-3, 10) and B (6, -8) in the ratio k : 1

Hence, the point P divides AB in the ratio 2 : 7.

Question 10.
The coordinates of the points P and Q are respectively (4, -3) and (-1, 7). Find the abscissa of a point R on the line segment PQ such that \(\frac{P R}{P Q}\) = \(\frac{3}{5}\).
Solution:

Coordinate Geometry Class 10 Extra Questions Short Answer Type 1

Question 1.
Write the coordinates of a point on x-axis which is equidistant from the points (-3, 4) and (2, 5).
Solution:
Let the required point be (x, 0).
Since, (x, 0) is equidistant from the points (-3, 4) and (2, 5) .

Question 2.
Find the values of x for which the distance between the points P (2, -3) and Q (x, 5) is 10.
Solution:

Question 3.
What is the distance between the points (10 cos 30°, 0) and (0, 10 cos 60°)?
Solution:

Question 4.
In Fig. 6.8, if A(-1, 3), B(1, -1) and C (5, 1) are the vertices of a triangle ABC, what is the length of the median through vertex A?
Solution:”

Question 5.
Find the ratio in which the line segment joining the points P (3, -6) and Q (5,3) is divided by the x-axis.
Solution:
Let the required ratio be λ : 1

Given that this point lies on the x-axis

Thus, the required ratio is 2 : 1.

Question 6.
Point P (5, -3) is one of the two points of trisection of the line segment joining the points A (7, -2) and B (1, -5). State true or false and justify your answer.
Solution:
Points of trisection of line segment AB are given by

∴ Given statement is true.

Question 7.
Show that ∆ABC, where A(-2, 0), B(2, 0), C(0, 2) and APQR where P(-4, 0), Q(4, 0), R(0,4) are similar triangles.
OR
Show that ∆ABC with vertices A(-2, 0), B(0, 2) and C(2, 0) is similar to ∆DEF with vertices D(-4, 0), F(4,0) and E(0, 4).
[∆PQR is replaced by ∆DEF]
Solution:

Question 8.
Point P (0, 2) is the point of intersection of y-axis and perpendicular bisector of line segment joining the points, A (-1, 1) and B (3, 3). State true or false and justify your answer.
Solution:
The point P (0, 2) lies on y-axis

AP ≠ BP
∴ P(0, 2) does not lie on the perpendicular bisector of AB. So, given statement is false.

Question 9.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
Let A (5,-2), B (6, 4) and C (7, -2) be the vertices of a triangle

Here, AB = BC
∴ ∆ABC is an isosceles triangle.

Question 10.
If (1, 2), (4, y), (x, 6) and (3,5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5) be the vertices of a parallelogram ABCD.
Since, the diagonals of a parallelogram bisect each other.

Hence, x = 6 and y = 3.

Question 11.
Find the ratio in which y-axis divides the line segment joining the points A(5, -6) and B(-1, 4). Also, find the coordinates of the point of division.
Solution:
Let the point on y-axis be P(0, y) and AP : PB = k : 1

Question 12.
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Solution:
∵ P divides AB in the ratio 1 : 2.

Question 13.
Find the ratio in which the point (-3, k) divides the line-segment joining the points (-5, 4) and (-2, 3). Also find the value of k.
Solution:
Let Q divide AB in the ratio of p : 1

Question 14.
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, -5) and R(-3, 6), find the coordinates of P.
Solution:
Let the point P be (2y, y)

Hence, coordinates of point P are (16, 8).

Question 15.
If two adjacent vertices of a parallelogram are (3, 2) and (-1, 0) and the diagonals intersect at (2, -5), then find the coordinates of the other two vertices.
Solution:
Let other two coordinates are (x, y) and (x’, y’)
O is mid point of AC and BD

Hence, co-ordinates are (1, -12) and (5, -10).

Coordinate Geometry Class 10 Extra Questions Short Answer Type 2

Question 1.
Determine, if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
Let A (1, 5), B (2, 3) and C (-2, -11) be the given points. Then we have

Clearly, AB + BC ≠ AC
∴ A, B, C are not collinear.

Question 2.
Find the distance between the following pairs of points:
(i) (-5, 7), (-1, 3)
(ii) (a, b), (-a, -b)
Solution:
(i) Let two given points be A (-5, 7) and B (-1, 3).
Thus, we have x₁ = -5 and x₂ = -1
y₁ = 7 and y₂ = 3

(ii) Let two given points be A (a,b) and B(-a, -b)
Here, x₁ = a and x₂ = -a; y₁ = b and y₂ = -b

Question 3.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for
your answer: (i) (-1, -2), (1, 0), (- 1, 2), (-3, 0) (ii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
(i) Let A(-1, -2), B(1, 0), C(-1, 2) and D(-3, 0) be the four given points.
Then, using distance formula, we have,

Hence, four sides of quadrilateral are equal and diagonals AC and BD are also equal.
∴ Quadrilateral ABCD is a square.

(ii) Let A (4, 5), B (7, 6), C (4, 3) and D (1, 2) be the given points. Then,

∴ ABCD is a parallelogram.

Question 4.
Find the value of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
OR
A line segment is of length 10 units. If the coordinates of its one end are (2, -3) and the abscissa of the other end is 10, find its ordinate.
Solution:
We have, PQ = 10

Squaring both sides, we have
⇒ (8)² + (y + 3)² = 100
⇒ (y + 3)² = 100 – 64
⇒ (y + 3)² = 36 or y + 3 ± 16
⇒ y + 3 = 6, y + 3 = -6 or y = 3, y = -9
Hence, values of y are – 9 and 3.

Question 5.
If Q(0, 1) is equidistant from P(5,-3) and R(x, 6) find the value of x. Also, find the distances of QR and PR.
Solution:
Since, point Q(0, 1) is equidistant from P(5, -3) and R(x, 6).
Therefore, QP = QR
Squaring both sides, we have, Qp² = QR²
⇒ (5 – 0)² + (-3 -1)² = (x – 0)² + (6 – 1)²
25 + 16 = x² + 25
x² = 16
∴ x = ±4
Thus, R is (4, 6) or (-4, 6).

Question 6.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
OR
Find the coordinates of a point on the x-axis which is equidistant from the points A(2, -5) and B(-2, 9).
Solution:
Let P(x, 0) be any point on x-axis.
Now, P(x, 0) is equidistant from point A(2,-5) and B(-2, 9)
∴ AP = BP

Squaring both sides, we have
(x – 2)² + 25 = (x + 2)² + 81
⇒ x² + 4 – 4x + 25 = x² + 4 + 4x + 81
⇒ -8x = 56
∴ x = \(\frac{56}{-8}\)
∴ The point on the x-axis equidistant from given points is (-7,0).

Question 7.
Find the relation between x and y, if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution:
Given points are A(x, y), B(1, 2) and C(7, 0)
These points will be collinear if the area of the triangle formed by them is zero.
Now, ar(∆ABC) = \(\frac{1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
⇒ 0 = \(\frac{1}{2}\) [x(2 – 0) + 1(0 – y) + 7(y – 2)]
⇒ 0 = \(\frac{1}{2}\) (2x – y + 7y – 14)
⇒ 2x + by – 14 = 0
⇒ x + 3y = 7, which is the required relation between x and y.

Question 8.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3,6) and (-3, 4).
Solution:
Let P(x, y) be equidistant from the points A(3, 6) and B(-3, 4)
i.e., PA = PB
Squaring both sides, we get
AP² = BP²
⇒ (x – 3)² + (y – 6)² = (x + 3)² + (1 – 4)²
⇒ x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 +y² – 8y + 16
⇒ -12x – 4y + 20 = 0
⇒ 3x + y – 5 = 0, which is the required relation.

Question 9.
Find the coordinates of the point which divides the line joining of (- 1, 7) and (4, – 3) in the ratio 2 : 3.
Solution:
Let P(x, y) be the required point. Thus, we have

So, the coordinates of P are (1, 3).

Question 10.
Find the coordinates of the points of trisection of the line segment joining (4, – 1) and (-2,-3).
Solution:
Let the given points be A(4, -1) and B(-2,-3) and points of trisection be P and Q.

Lęt AP = PQ = QB = k
PB = PQ + QB = k + k = 2k
AP : PB = k : 2k = 1 : 2.
Therefore, coordinates of P are

Question 11.
Find the ratio in which the line segment joining A(1, -5) and B(-4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Solution:
Let the required ratio bek: 1. Then, the coordinates of the point of division is

Question 12.
The points A(4, -2), B(7, 2), C(0, 9) and D(-3, 5) form a parallelogram. Find the length of the altitude of the parallelogram on the base AB.
Solution:
Let, DE = h be the height of parallelogram ABCD w.r.t. base AB.

Question 13.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Solution:
Let the coordinates of A be (x, y)
Now, C is the centre of circle therefore, the coordinates of

Hence, coordinates of A are (3, -10).

Question 14.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AB = 5 AB and P lies on the line segment AB.
Solution:

Question 15.
Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts (Fig. 6.21).
Solution:
Let P, Q, R be the points that divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.

Since, Q divides the line segment AB into two equal parts, i.e., Q is the mid-point of AB.

Question 16.
Find the area of a rhombus if its vertices (3, 0), (4, 5), (- 1, 4) and (-2, – 1) are taken in order.
Solution:
Let A(3, 0), B(4, 5), C(-1, 4) and D(-2, -1) be the vertices of a rhombus.
Therefore, its diagonals

Question 17.
Find the area of the triangle whose vertices are: (-5, -1), (3, -5), (5, 2)
Solution:
Let A(x₁, y₁) = (-5, -1), B(x₂, y₂) = (3 – 5), C(x₃, y₃) = (5, 2)
∴ area of ∆ABC = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)(-5(-5 – 2) + 3 (2 + 1) + 5(-1 + 5)]
= \(\frac{1}{2}\)(35 + 9 + 20) = \(\frac{1}{2}\) × 64 = 32 sq units.

Question 18.
If the point A (0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also find the length of AB.
Solution:
Given that A (0, 2) is equidistant from B (3, p) and C (p, 5)
∴ AB = AC
or
AB² = AC²
(3 – 0)² + (0 – 2)² = (p – 0)² + (5 – 2)²
3² + p² + 4 – 4p = p² + 9
= 4 – 4p = 0
⇒ 4p = 4
⇒ p = 1

Question 19.
If the points A (-2, 1), B (a, b) and C (4, -1) are collinear and a – b = 1, find the values of a and b.
Solution:
Since the given points are collinear, then area of ∆ABC = 0
⇒ \(\frac{3}{5}\)[x1 ( y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
Given, x₁ = -2, y₁ = 1, x₂ = 0, y₂ = b, x₃ = 4, y₃ = -1
Putting the values,
\(\frac{1}{2}\)[-2(b + 1) + a(-1 – 1) + 4(1 – b)] = 0
⇒ -26 – 2 – 2a + 4- 4b = 0
⇒ 2a + 65 = 2
a + 3b = 1 ….. (i)
Given, a – b = 1 … (ii)
Subtracting (i) from (ii), we have
– 4b = 0
⇒ b = 0
Substituting the value of b in (ii), we have a = 1.

Question 20.
If the point P (k-1, 2) is equidistant from the points A (3, k) and B (k, 5), find the values of k.
Solution:
Let the given line segment be divided by point Q. Since P is equidistant from A and B,
AP = BP or Ap² = BP²
[3 – (k – 1)]² + (k – 2)² = [k – (k – 1)]² + (5 – 2)²
(3 – k + 1)² + (k – 2)² = (k – k + 1)² + (3)²
(4 – k)² + (k – 2)² = (1)² + (3)²
⇒ 16 + k² – 8k + k² + 4 – 4k = 1 + 9
⇒ 2k² – 12k + 20 = 10
⇒ k² – 6k + 10 = 5
⇒ ķ² – 6k + 5 = 0
⇒ k² – 5k – k + 5 = 0
⇒ k (k – 5) -1(k – 5) = 0
⇒ k = 1 or k = 5

Question 21.
Find the ratio in which the line segment joining the points A(3, -3) and B(-2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Solution:

Here, point Q is on x-axis so its ordinate is O.
Let ratio be k : 1 and coordinate of point Q be (x, 0)

We are given that A(3, -3) and B(-2, 7)

Question 22.
Find the values of k if the points Ask + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
Solution:
Points Ask + 1, 2k), B (3k, 2k + 3) and C (5k – 1, 5k) are collinear
∴ Area of ∆ABC = 0

Question 23.
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Solution:
Given, PA = PB or (PA)² = (PB)²
(a + b – x)² + (b – a – y)² = (a – b – x)² + (a + b – y)²
⇒ (a + b)² + x² – 2ax – 25x + (b – a)² + y² – 2by + 2ay
⇒ (a – b)² + x² – 2ax + 2bx + (a + b)² + y² – 2ay – 2by
⇒ 4ay = 4bx or bx = ay
Hence proved.

Question 24.
If the point C(-1, 2) divides internally the line segment joining the points A(2, 5) and B(x, y) in the ratio of 3 : 4, find the value of x² + y².
Solution:

Question 25.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
Solution:

Since AB = BC = AC = 3 units
∴ Co-ordinates of B are (5, 0)
Let co-ordinates of C be (x, y)
AC² = BC²
[∵ ∆ABC is an equilateral triangle]
Using distance formula
⇒ (x – 2)² + (y – 0)² = (x – 5)² + (y – 0)²
⇒ x²+ 4 – 4x + y = x²+ 25 – 10x + y² 6x = 21
⇒ x = \(\frac{21}{6}\) = \(\frac{7}{2}\)
Again (x – 2)² + (y – 0)² = 9

Coordinate Geometry Class 10 Extra Questions Long Answer Type

Question 1.
Find the value of ‘k”, for which the points are collinear: (7, -2), (5, 1), (3, k).
Solution:
Let the given points be
A (x₁, y₁) = (7, -2), B (x₂, Y₂) = (5, 1) and C (x₃, y₃) = (3, k)
Since these points are collinear therefore area (∆ABC) = 0
⇒ \(\frac{1}{2}\) [x₁(y₂ – Y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
⇒ x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂) = 0
⇒ 7(1 – k) + 5(k + 2) + 3(-2 -1) = 0
⇒ 7 – 7k + 5k + 10 – 9 = 0
⇒ -2k + 8 = 0
⇒ 2k = 8
⇒ k = 4
Hence, given points are collinear for k = 4.

Question 2.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution:
Let A (x₁, y₁) = (0, -1), B (x₂, y₂) = (2, 1), C (x₃, y₃) = (0, 3) be the vertices of ∆ABC.
Now, let P, Q, R be the mid-points of BC, CA and AB, respectively.
So, coordinates of P, Q, R are

Ratio of ar (∆PQR) to the ar (∆ABC) = 1 : 4.

Question 3.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Solution:

Let A(4, -2), B(-3, -5), C(3, -2) and D(2, 3) be the vertices of the quadrilateral ABCD.
Now, area of quadrilateral ABCD
= area of ∆ABC + area of ∆ADC

Question 4.
A median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A (4,-6), B (3, -2) and C (5, 2).
Solution:
Since AD is the median of ∆ABC, therefore, D is the mid-point of BC.

Hence, the median divides it into two triangles of equal areas.

Question 5.
Find the ratio in which the point P (x, 2), divides the line segment joining the points A (12, 5) and B (4, -3). Also find the value of x.
Solution:

The ratio in which p divides the line segment is \(\frac{3}{5}\), i.e., 3 : 5.

Question 6.
If A (4, 2), B (7, 6) and C (1, 4) are the vertices of a ∆ABC and AD is its median, prove that the median AD divides into two triangles of equal areas.
Solution:
Given: AD is the median on BC.
⇒ BD = DC
The coordinates of midpoint D are given by.

Hence, AD divides ∆ABC into two equal areas.

Question 7.
If the point A (2, -4) is equidistant from P (3, 8) and Q (-10, y), find the values of y. Also find distance PQ.
Solution:
Given points are A(2, 4), P(3, 8) and Q(-10, y)
According to the question,
PA = QA

Question 8.
The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of point Care (0, -3). The origin is the mid-point of the base. Find the coordinates of the points A and B. Also find the coordinates of another point D such that BACD is a rhombus.
Solution:
∵ O is the mid-point of the base BC.
∴ Coordinates of point B are (0, 3). So,
BC = 6 units Let the coordinates of point A be (x, 0).
Using distance formula,

∴ Coordinates of point A = (x, 0) = (3√3, 0)
Since BACD is a rhombus.
∴ AB = AC = CD = DB
∴ Coordinates of point D = (-3√3, 0).

Question 9.
Prove that the area of a triangle with vertices (t, t-2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Solution:
Area of a triangle = \(\frac{1}{2}\) [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
Area of the triangle = \(\frac{1}{2}\)[t + 2 – t) + (t + 2) (t – t + 2) + (t + 3) (t – 2 – t – 2)]
= \(\frac{1}{2}\) [2t + 2t + 4 – 4t – 12 ]
= 4 sq. units
which is independent of t.
Hence proved.

Question 10.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, -2). If the third vertex is (\(\frac{7}{2}\), y), find the value of y.
Solution:
Given: ar(∆ABC) = 5 sq. units

Question 11.
The coordinates of the points A, B and Care (6, 3), (-3,5) and (4,-2) respectively. P(x, y) is any point in the plane. Show that \(\frac { ar(∆PBC) }{ ar(∆ABC) } \) = \(\frac{x+y-2}{7}\)
Solution:
P(x, y), B(-3, 5), C(4, -2), A(6, 3)

Question 12.
In Fig. 6.32, the vertices of ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{3}\) Calculate the area of ∆ADE and compare it with area of ∆ABC.
Solution:

\

Question 13.
If a = b = 0, prove that the points (a, a²), (b, b²) (0, 0) will not be collinear.
Solution:
∵ We know that three points are collinear if area of triangle = 0
∴ Area of triangle with vertices (a, a²), (b, b²) and (0, 0)

∵ Area of ∆ ≠ 0
∴ Given points are not collinear.

Coordinate Geometry Class 10 Extra Questions HOTS

Question 1.
The line joining the points (2, 1) and (5, -8) is trisected by the points P and Q. If the point P lies on the line 2x – y + k = 0, find the value of k.
Solution:

As line segment AB is trisected by the points P and Q.
Therefore,
Case I: When AP : PB = 1 : 2.

⇒ P (3, -2)
Since the point P (3,-2) lies on the line
2x – y + k = 0 =
⇒ 2 × 3-(-2) + k = 0
⇒ k = -8

Case II: When AP : PB = 2 : 1.

Coordinates of point P are

Since the point P(4, -5) lies on the line
2x – y + k = 0
∴ 2 × 4-(-5) + k = 0
∴ k = -13

Question 2.
Prove that the diagonals of a rectangle bisect each other and are equal.
Solution:

Let OACB be a rectangle such that OA is along x-axis and OB is along y-axis. Let OA = a and OB = b.
Then, the coordinates of A and B are (a,0) and (0, b) respectively.
Since, OACB is a rectangle. Therefore,
AC = OB
⇒ AC = b
Also, OA = a
⇒ BC = a
So, the coordinates of Care (a, b).

∴ OC = AB.

Question 3.
In what ratio does the y-axis divide the line segment joining the point P (4, 5) and Q (3, -7)?
Also, find the coordinates of the point of intersection.
Solution:
Suppose y-axis divides PQ in the ratio k : 1. Then, the coordinates of the point of division are|

Question 4.
Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).
Solution:
Let O(x, y) be the centre of circle. Given points are A(6, -6), B(3, -7) and C(3, 3).

Question 5.
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4). Find its centroid.
Solution:

Let P(1, 1), Q(2, -3), R(3, 4) be the mid-points of sides AB, BC and CA respectively, of triangle ABC. Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of triangle ABC. Then, P is the mid-point of AB.

Question 6.
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).
Solution:
Let P(x₁, y₁) be common point of both lines and divide the line segment joining A(2, -2) and B(3, 7) in ratio k : 1.

Question 7.
Show that ∆ABC with vertices A (-2, 0), B (2, 0) and C (0, 2) is similar to ∆DEF with vertices
D(4, 0) E (4, 0) and F (0, 4).
Solution:
Given vertices of ∆ABC and ∆DEF are

A(-2, 0), B(2, 0), C(0, 2), D(-4, 0), E(4, 0) and F(0, 4)


Here, we see that sides of ∆DEF are twice the sides of a ∆ABC.
Hence, both triangles are similar.

Here we are providing Pair of Arithmetic Progressions Class 10 Extra Questions Maths Chapter 5 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Arithmetic Progressions with Answers Solutions

Extra Questions for Class 10 Maths Chapter 5 Arithmetic Progressions with Solutions Answers

Arithmetic Progressions Class 10 Extra Questions Very Short Answer Type

Question 1.
Which of the following can be the n^th term of a_n AP?
4n + 3, 3n² + 5, n² + 1 give reason.
Solution:
4n + 3 because n^th term of a_n AP ca_n only be a linear relation in n as a_n = a + (n – 1)d.

Question 2.
Is 144 a term of the AP: 3, 7, 11, …? Justify your answer.
Solution:
No, because here a = 3 a_n odd number and d = 4 which is even. so, sum of odd and even must be odd whereas 144 is a_n even number.

Question 3.
The first term of a_n AP is p and its common difference is q. Find its 10^th term.
Solution:
210 = a + 9d = p + 99.

Question 4.
For what value of k: 2k, k + 10 and 3k + 2 are in AP?
Solution:
Given numbers are in AP
∴ (k + 10) – 2k = (3k + 2) – (k + 10)
⇒ -k + 10 = 2k – 8 or 3k = 18 or k = 6.

Question 5.
If a_n = 5 – 11n, find the common difference.
Solution:
We have a_n = 5 – 11n
Let d be the common difference
d = a_n+1 – a_n
= 5 – 11(n + 1) – (5 – 11n)
= 5 – 11n – 11 -5 + 11n = -11

Question 6.
If n^th term of a_n AP is \(\frac{3+n}{4}\) find its 8^th term.
Solution:

Question 7.
For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of AP?
Solution:
since 20 + 1, 13, 5p – 3 are in AP.
∴ second term – First term = Third term – second term
⇒ 13 – (2p + 1) = 5p – 3 – 13
⇒ 13 – 2p – 1 = 5p – 16
⇒ 12 – 2p = 5p – 16
⇒ -7p = – 28
⇒ p = 4

Question 8.
In a_n AP, if d = -4, n = 7, a, = 4 then find a.
Solution:
We know, a_n = a + (n – 1)d
Putting the values given, we get
⇒ 4 = a + (7 – 1)(-4) or a = 4 + 24
⇒ a = 28

Question 9.
Find the 25^th term of the AP: -5, \(\frac{-5}{2}\) , 0, \(\frac{-5}{2}\) ………
Solution:
Here, a = -5, b = –\(\frac{5}{2}\) – (-5) = \(\frac{5}{2}\)
We know,
a₂₅ = a + (25 – 1 )d
= (-5) + 24(\(\frac{5}{2}\)) = -5 + 60 = 55

Question 10.
Find the common difference of an AP in which a₁₈ – a₁₄ = 32.
Solution:
Given, a₁₈ – a₁₄ = 32
⇒ (a + 17d) – (a + 13d) = 32
⇒ 17d – 13d = 32 or d = \(\frac{32}{4}\)

Question 11.
If 7 times the 7^th term of an AP is equal to 11 times its 11^th term, then find its 18^th term.
Solution:
Given, 7a₇= 11a₁₁
⇒ 7(a + 6d) = 11(a + 100) or 7a + 42d = 11a + 110d
⇒ 4a + 68d = 0 or a + 17d = 0
Now, a₁₈ = a + 17d = 0

Question 12.
In an AP, if a = 1, a_n = 20, and s_n = 399, then find n.
Solution:
Given, An = 20
= 1 + (n – 1)d = 20
⇒ (n – 1) d = 19
s_n = \(\frac{n}{2}\) {2a + (n – 1)d}
⇒ 399 = \(\frac{n}{2}\){2 × 1 + 19}
⇒ \(\frac{399 \times 2}{21}\) = n
⇒ n = 38

Question 13.
Find the 9th term from the end (towards the first term) of the AP 5, 9, 13, …, 185.
Solution:
l = 185, d = 4
l₉ = l – (n – 1) d
= 185 – 8 × 4 = 153

Arithmetic Progressions Class 10 Extra Questions Short Answer Type 1

Question 1.
In which of the following situations, does the list of numbers involved to make an AP? If yes, give a reason.
(i) The cost of digging a well after every meter of digging, when it costs 150 for the first meter and rises by 50 for each subsequent meter.
(ii) The amount of money in the account every year, when 10,000 is deposited at simple interest at 8% per annum.
Solution:
(i) The numbers involved are 150, 200, 250, 300, …
Here 200 -150 = 250 – 200 = 300 – 250 and so on
∴ It forms a_n AP with a = 150, d = 50

(ii) The numbers involved are 10,800, 11,600, 12,400, …
which forms a_n AP with a = 10,800 and d = 800.

Question 2.
Find the 20^th term from the last term of the AP: 3, 8, 13, …, 253.
Solution:
We have, last term = 1 = 253
And, common difference d = 2^nd term – 1^st term = 8 – 3 = 5
Therefore, 20^th term from end = 1 -(20 – 1) × d = 253 – 19 × 5 = 253 – 95 = 158.

Question 3.
If the sum of the first p terms of an AP is ap² + bp, find its common difference.
Solution:
a_p = s_p – s_p-1 = (ap² + bp) -[a(p – 1)² + b(p – 1)]
= ap² + bp – (ap² + a – 2ap + bp – b)
= ap² + bp – ap² – a + 2ap – bp + b = 2ap + b-a .
= a₁ = 2a + b – a = a + b and a₂ = 4a + b – a = 3a + b
⇒ d = a₂ – a₁ = (3a + b) – (a + b) = 2a

Question 4.
The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.
Solution:
Let the first term be ‘a’ and common difference be ‘d’.
Given, a = 5, T_n = 45, s_n = 400 .
Tn = a + (m – 1)d
⇒ 45 = 5 + (m – 1)d
⇒ (n – 1) d = 40 ………(i)
s_n = \(\frac{n}{2}\) (a + T_n)
⇒ 400 = \(\frac{n}{2}\) (5 + 45)
⇒ n = 2 × 8 = 16 substituting the value of n in (i)
⇒ (16 – 1)d = 40
⇒ d = \(\frac{40}{15}\) = \(\frac{8}{3}\)

Question 5.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Solution:
Natural numbers between 101 and 999 divisible by both 2 and 5 are 110, 120, … 990.
so, a1 = 110, d = 10, a_n = 990
We know, a_n = a₁ + (n – 1)d
990 = 110 + (n – 1) 10
(n – 1) = \(\frac{990-110}{10}\)
⇒ n = 88 + 1 = 89

Question 6.
Find how many integers between 200 and 500 are divisible by 8.
Solution:
AP formed is 208, 216, 224, …, 496
Here, a_n = 496, a = 208, d = 8
a_n = a + (n – 1) d
⇒ 208 + (n – 1) x 8 = 496
⇒ 8 (n – 1) = 288
⇒ n – 1 = 36
⇒ n = 37

Question 7.
The sum of the first n terms of an AP is 3n² + 6n. Find the nth term of this
Solution:
Given: s_n = 3n² +6n
s_n-1 = 3(n – 1)² + 6(n – 1)
⇒ 3(n² + 1 – 2n) + 6n – 6
⇒ 3m2 + 3 – 6n + 6n – 6 = 3n² – 3
The n^th term will be a_n
s_n = s_n-1 + a_n
a_n = s_n – s_n-1
⇒ 3n² + 6n – 3n² + 3
⇒ 6n + 3

Question 8.
How many terms of the AP 18, 16, 14, …. be taken so that their sum is zero?
Solution:
Here, a = 18, d = -2, s_n = 0
Therefore, \(\frac{n}{2}\) [36 + (n – 1) (- 2)] = 0
⇒ n(36 – 2n + 2) = 0
⇒ n(38 – 2n) = 0
⇒ n = 19

Question 9.
The 4th term of an AP is zero. Prove that the 25^th term of the AP is three times its 11th term.
Solution:
∵ a₄ = 0 (Given)
⇒ a + 3d = 0
⇒ a = -3d
a₂₅ = a + 24d = – 3d + 24d = 21d
3a₁₁ = 3(a + 100) = 3(70) = 21d
∴ a₂₅ = 30₁₁
Hence proved.

Question 10.
If the ratio of sum of the first m and n terms of an AP is m² : n², show that the ratio of its mth and n^th terms is (2m – 1) : (2n – 1).
Solution:

Question 11.
What is the common difference of an AP in which a₂₁ – a₇ = 84?
Solution:
Given: a₂₁ – a₇ = 84
⇒ (a + 20d) – (a + 6d) = 84
⇒ 14d = 84
⇒ d = 6

Question 12.
For what value of n, are the n^th terms of two APs 63, 65, 67,… and 3, 10, 17,… equal?
Solution:
Let nth terms for two given series be a_n and a’_n
According to questions
a_n = a’_n
⇒ a + (n – 1)d = a + (n – 1)d’
⇒ 63 + (n – 1)2 = 3 + (n – 1)7
⇒ 5n = 65
⇒ n = 13.

Arithmetic Progressions Class 10 Extra Questions Short Answer Type 2

Question 1.
Which term of the AP: 3, 8, 13, 18, … , is 78?
Solution:
Let a_n be the required term and we have given AP
3, 8, 13, 18, …..
Here, a = 3, d = 8 – 3 = 5 and a_n = 78
Now, a_n = a + (n – 1)d
⇒ 78 = 3 + (n – 1) 5
⇒ 78 – 3 = (n – 1) × 5
⇒ 75 = (n – 1) × 5
⇒ \(\frac{75}{5}\) = n – 1
⇒ 15 = n – 1
⇒ n = 15 + 1 = 16
Hence, 16^th term of given AP is 78.

Question 2.
Find the 31^st term of an AP whose 11^th term is 38 and the 16^th term is 73.
Solution:
Let the first term be a and common difference be d.
Now, we have

Putting the value of d in equation (i), we have
a + 10 × 7 = 38
⇒ a + 70 = 38
⇒ a = 38 – 70
⇒ a = – 32
We have, a = -32 and d = 7
Therefore, a₃₁ = a + (31 – 1)d
⇒ a₃₁ = a + 30d
⇒ (-32) + 30 × 7
⇒ – 32 + 210
= a₃₁ = 178

Question 3.
An AP consists of 50 terms of which 3^rd term is 12 and the last term is 106. Find the 29^th term.
Solution:
Let a be the first term and d be the common difference.
since, given AP consists of 50 terms, so n = 50
a₃ = 12
⇒ a + 2d = 12 …(i)
Also, a₅₀ = 106
⇒ a + 490 = 106 … (ii)
subtracting (i) from (ii), we have
47d = 94
⇒ d = \(\frac{94}{47}\) = 2
Putting the value of d in equation (i), we have
a + 2 × 2 = 12
⇒ a = 12 – 4 = 8
Here, a = 8, d = 2
∴ 29th term is given by
a₂₉ = a + (29 – 1)d = 8 + 28 × 2
⇒ a₂₉ = 8 + 56
⇒ a₂₉ = 64

Question 4.
If the 8th term of an AP is 31 and the 15^th term is 16 more than the 11^th term, find the AP.
Solution:
Let a be the first term and d be the common difference of the AP.
We have, a₈ = 31 and a₁₅ = 16 + a₁₁
⇒ a + 7d = 31 and a + 14d = 16 + a + 10d
⇒ a + 7d = 31 and 4d = 16
⇒ a + 7d = 31 and d = 4
⇒ a + 7 × 4 = 31
⇒ a + 28 = 31
⇒ a= 3
Hence, the AP is a, a + d, a + 2d, a + 3d…..
i.e., 3, 7, 11, 15, 19, …

Question 5.
Which term of the arithmetic progression 5, 15, 25, …. will be 130 more than its 31^st term?
Solution:
We have, a = 5 and d = 10
∴ a₃₁ = a + 30d = 5 + 30 × 10 = 305
Let n^th term of the given AP be 130 more than its 31^st term. Then,
a_n = 130 + a₃₁
∴ a + (n – 1)d = 130 + 305
⇒ 5 + 10(n – 1) = 435
⇒ 10(n – 1) = 430
⇒ n – 1 = 43
⇒ n = 44
Hence, 44^th term of the given AP is 130 more than its 31^st term.

Question 6.
Which term of the progression \(20,19 \frac{1}{4}, 18 \frac{1}{2}, 17 \frac{3}{4}\), is the first negative term?
Solution:

Question 7.
Find the sum given below:
7 + 10 \(\frac{1}{2}\) + 14 +…+ 84
Solution:
Let a be the first term, d be the common difference and a_n be the last term of given AP.

Question 8.
In an AP: given l = 28, s = 144, and there are total 9 terms. Find a.
Solution:
We have, l = 28, s = 144 and n = 9
Now, l = a_n = 28
28 = a + (n – 1) d 28 = a + (9 – 1)d
⇒ 28 = a + 8d ……(i)
and S = 144
⇒ 141 = \(\frac{1}{2}\) [2a + (n – 1)d]
⇒ 144 = \(\frac{9}{2}\) [12a +(9 – 1) d]
\(\frac{144 \times 2}{9}\) = 2a + 8d
⇒ 32 = 2a + 8d
⇒ 16 = a + 4d … (ii)
Now, subtracting equation (ii) from (i), we get
4d = 12 or d = 3
Putting the value of d in equation (i), we have
a + 8 × 3 = 28
⇒ a + 24 = 28
⇒ a = 28 – 24
∴ a = 4.

Question 9.
How many terms of the AP: 9, 17, 25, … must be taken to give a sum of 636?
Solution:
Let sum of n terms be 636.
s_n = 636, a = 9, d = 17 – 9 = 8
⇒ \(\frac{n}{2}\)[2a + (n – 1) d] = 636
⇒ \(\frac{n}{2}\)[2 x 9 + (n – 1) × 8] = 636
⇒ \(\frac{n}{2}\) × 2[9+ (n – 1) 4] = 636
⇒ n[9 + 4n – 4] = 636
⇒ n[5 + 4n] = 636
⇒ 5n + 4n² = 636
⇒ 4n² + 5n – 636 = 0

Thus, the sum of 12 terms of given AP is 636.

Question 10.
How many terms of the series 54, 51, 48 ……. be taken so that, their sum is 513? Explain the
double answer.
Solution:
Clearly, the given sequence is an AP with first term a = 54 and common difference d = -3. Let
the sum of n terms be 513. Then,
s_n = 513
⇒ \(\frac{n}{2}\) {2a + (n – 1) d} = 513
⇒ \(\frac{n}{2}\) (108 + (n – 1) – 3) = 513
⇒ n[108 – 3n + 3) = 1026
⇒ -3n² + 111n = 1026
⇒ n² – 37n + 342 = 0
⇒ (n – 18) (n – 19) = 0
⇒ n = 18 or 19
Here, the common difference is negative. so, 19th term is given by
a₁₉ = 54 + (19 – 1) × – 3 = 0
Thus, the sum of 18 terms as well as that of 19 terms is 513.

Question 11.
The first term, common difference and last term of an AP are 12, 6 and 252 respectively. Find the sum of all terms of this AP.
Solution:
We have, a = 12, d = 6 and l = 252
Now, l = 252
⇒ a_n = 252
= l = a + (n – 1)d
⇒ 252 = 12 + (n – 1) × 6
⇒ 240 = (n – 1) × 6
⇒ n – 1 = 40 or n = 41
Thus, S_n = \(\frac{n}{2}\)(a + l)
⇒ S₄₁ = \(\frac{41}{2}\)(12 + 252) = \(\frac{41}{2}\) (264) = 41 × 132 = 5412

Question 12.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
Solution:
We have, S₇ = 49
⇒ 49 = \(\frac{7}{2}\)[2a + (7 – 1) × d]
⇒ 49 × \(\frac{2}{7}\) = 2a + 6d
⇒ 14 = 2a + 6d
⇒ a + 3d = 7
and S₁₇ = 289
⇒ 289 = \(\frac{17}{2}\) [2a + (17 – 1)d]
⇒ 2a + 16d = \(\frac{289 \times 2}{17}\) = 34
⇒ a + 8d = 17
Now, subtracting equation (i) from (ii), we have
5d = 10 ⇒ d = 2
Putting the value of d in equation (i), we have
a + 3 × 2 = 7
⇒ a = 7 – 6 = 1
Here, a = 1 and d = 2
Now, s_n = \(\frac{n}{2}\) [2a + (n – 1) d]
= \(\frac{n}{2}\) [2 × 1 + (n – 1) × 2]
= \(\frac{n}{2}\)[2 + 2n – 2]
= \(\frac{n}{2}\) × 2n = n²

Question 13.
The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Solution:

Question 14.
If the seventh term of an AP is a and its ninth term is, find its 63^rd term.
Solution:

Question 15.
The sum of the 5^th and the 9^th terms of an AP is 30. If its 25^th term is three times its 8^th term, find the AP.
Solution:
a₅ + a₉ = 30
⇒ (a + 4d) + (a + 8d) = 30 = 2a + 12d = 30
⇒ a + 6d = 15
a = 15 – 6d …(i)
a₂₅ = 3a₈
⇒ a + 24d = 3(a + 7d)
á + 24d = 3a + 21d
⇒ 2a = 3d
Putting the value of a form (i), we have
2(15 – 6d) = 3d
⇒ 30 – 12d = 3d
⇒ 15d = 30
⇒ d = 2
So, a = 15 – 6 × 2 = 15 – 12 [From equation (i)]
⇒ a = 3
The AP will be 3, 5, 7, 9….

Question 16.
The sum of the first 7 terms of an AP is 63 and the sum of its next 7 terms is 161. Find the 28^th term of this AP.
Solution:
sum of first seven terms,

Question 17.
If the ratio of the sum of first n terms of two AP’s is (7n + 1): (4n + 27), find the ratio of their mth terms.
Solution:

Question 18.
Find the sum of the following series :
5 + (-41) + 9 + (-39) + 13 + (-37) + 17 + … + (-5) + 81 + (-3)
Solution:
The series can be rewritten as,
(5 + 9 + 13 + … +81) + (41 + (-39) + (-37) + … + (-5) + (-3))
For the series 5 + 9 + 13 + … 81
a = 5, d = 4 and a_n = 81
nth term = a + (n – 1)d = a_n
⇒ 5+ (n – 1)4 = 81
⇒ 4n = 80
⇒ n =
20 sum of 20 terms for this series.
s_n = \(\frac{20}{2}\) (5 + 81) = 860 …(i)
[∵ s_n = \(\frac{n}{2}\) (a + a_n)]
For the series (41) + (-39) + (-37)… + (-5) + (-3)
a = 41, d = 2 and and = -3
nth term = a + (n – 1)d = a_n.
⇒ -41 + (n – 1)2 = -3
⇒ 2n = 40
⇒ n = 20
sum of 20 terms for this series
s_n = \(\frac{20}{2}\) (-41 – 3) = – 440 …(ii)
By adding (i) and (ii), we get
sum of series = 860 – 440
= 420

Question 19.
Find the sum of all two digit natural numbers which are divisible by 4.
Solution:
Here a = 12, d = 4, a_n = 96
The formula is a_n = a + (n – 1)d
Therefore 96 = 12 + (n – 1) × 4
⇒ 96 = 8 + 4n
⇒ n = \(\frac{88}{4}\)
⇒ n = 22
Apply the formula for sum,
s_n = \(\frac{n}{2}\) [2a + (n – 1)d]
Hence, s₂₂ = 11/24 + 21 × 4] = 11[24 + 84]
= 11 × 108 = 1188.

Arithmetic Progressions Class 10 Extra Questions Long Answer Type

Question 1.
The sum of the 4^th and 8^th term of an AP is 24 and the sum of the 6th and 10th term is 44. Find the first three terms of the AP.
Solution:
We have, a₄ + a₈ = 24
⇒ a + (4 – 1)d + a + (8 – 1) d = 24
⇒ 2a + 3d + 7d = 24
⇒ 2a + 10d = 24
⇒ 2(a + 5d) = 24
∴ a + 5d = 12
and, a₆ + a₁₀ = 44
⇒ a + (6 – 1)d + a + (10 – 1) d = 44
⇒ 2a + 5d + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22
subtracting (i) from (ii), we have
2d = 10
∴d = \(\frac{10}{2}\) = 5
Putting the value of d in equation (i), we have
a + 5 × 5 = 12
⇒ a = 12 – 25 = -13
Here, a = -13, d = 5
Hence, first three terms are
-13, -13, + 5, -13 + 2 × 5 i.e., -13, -8, -3

Question 2.
The sum of the first n terms of an AP is given by s_n = 3n² – 4n. Determine the AP and the 12^th term.
Solution:
We have, s_n = 3n² – 4n …(i)
Replacing n by (n – 1), we get
s_n-1 = 3(n – 1)² – 4(n – 1) ….(ii)
We know, .
a_n = s_n – s_n-1 = {3n² – 4n} – {3(n – 1)² – 4(n – 1)}.
= {3n² – 4n} – {3n² + 3 – 6n – 4n + 4}
= 3n² – 4n – 3n² – 3 + 6n + 4n – 4 = 6n – 7
so, nth term a_n = 6n – 7
To get the AP, substituting n = 1, 2, 3… respectively in (iii), we get
a₁ = 6 × 1-7 = -1,
a₂ = 6 × 2 – 7 = 5
a₃ = 6 × 3 – 7 = 11,…
Hence, AP is – 1,5, 1:1, …
Also, to get 12th term, substituting n = 12 in (iii), we get
a₁₂ = 6 × 12 – 7 = 72 – 7 = 65

Question 3.
Divide 56 into four parts which are in AP such that the ratio of product of extremes to the product of means is 5 : 6.
Solution:
Let the four parts be a – 3d, a-d, a + d, a + 3d.
Given, (a – 3d) + (a – d) + (a + d) + (a + 3d) = 56

Question 4.
In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.
Solution:
Let ‘a’ be the first term and ‘d be the common difference.

Question 5.
If s, denotes the sum of the first n terms of an AP, prove that s₃₀ = 3 (s₂₀ – s₁₀).
Solution:

Question 6.
A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief?
Solution:
Let total time be n minutes
Total distance covered by thief = 100 n metres
Total distance covered by policeman = 100 + 110 + 120 + … + (n – 1) terms
∴ 100m = \(\frac{n-1}{2}\) [100(2) + (n – 2)10]
⇒ 200n = (n – 1)(180 + 10n)
⇒ 10²– 30n – 180 = 0
⇒ n² – 3n – 18 = 0
⇒ (n-6) (n + 3) = 0
⇒ n = 6
Policeman took (n – 1) = (6 – 1) = 5 minutes to catch the thief.

Question 7.
The houses in a row are numbered consecutively from 1 to 49. show that there exists a value of X such that sum of numbers of houses preceeding the house numbered X is equal to sum of the numbers of houses following X. Find value of X.
Solution:
The numbers of houses are 1, 2, 3, 4……….49.
The numbers of the houses are in AP, where a = 1 and d = 1
sum of n terms of an AP = \(\frac{n}{2}\)[2a + (n – 1)d]
Let X^th number house be the required house.
sum of number of houses preceding X^th house is equal to s_x-1 i.e.,

since number of houses is positive integer,
∴ X = 35

Question 8.
If the ratio of the 11^th term of an AP to its 18th term is 2:3, find the ratio of the sum of the first five terms to the sum of its first 10 terms.
Solution:

Arithmetic Progressions Class 10 Extra Questions HOTS

Question 1.
Find the sum of the first 15 multiples of 8.
Solution:
The first 15 multiples of 8 are
8, 16, 24, … 120
Clearly, these numbers are in AP with first term a = 8 and common difference, d = 16 – 8 = 8

Question 2.
Find the sum of all two digit natural numbers which when divided by 3 yield 1 as remainder.
Solution:
Two digit natural numbers which when divided by 3 yield 1 as remainder are:
10, 13, 16, 19, …, 97, which forms an AP.
with a = 10, d = 3, a_n = 97
a_n = 97 = a + (n – 1) d = 97
or 10 + (n – 1)3 = 97
⇒ (n – 1) = \(\frac{87}{3}\) = 29
⇒ n = 30
Now, s₃₀ = [2 × 10 + 29 × 3) = 15(20 + 87) = 15 × 107 = 1605

Question 3.
A sum of ₹700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes.
Solution:
Let the prizes be a + 60, a + 40, a + 20, a, a – 20, a – 40, a – 60
Therefore, the sum of prizes is
a + 60 + a + 40 + a + 20 + a ta – 20 + a – 40 +a – 60 = 700
= 7a = 700
⇒ a = \(\frac{700}{7}\) = 100
Thus, the value of seven prizes are
100 + 60, 100 + 40, 100 + 20, 100, 100 – 20, 100 – 40, 100 – 60
i.e., ₹160, ₹140, ₹120, ₹100, ₹80, ₹60, ₹340

Question 4.
If the mth term of an AP is \(\frac{1}{n}\) and nth term is \(\frac{1}{m}\), then show that its (mn)th term is 1.
Solution:
Let a and d be the first term and common difference respectively of the given AP. Then
a_m = a + (m – 1) d
⇒ a + (m – 1)d = \(\frac{1}{n}\) …… (i)

Question 5.
If the sum of m terms of a_n AP is the same as the sum of its n terms, show that the sum of its (m + n) terms is zero.
Solution:
Let a be the first term and d be the common difference of the given AP.
Then, s_m = s_n

Question 6.
The ratio of the sums of m and n terms of a_n AP is m² : n². show that the ratio of the mth and nth terms is (2m – 1): (2n – 1).
Solution:
Let a be the first term and d the common difference of the given AP. Then, the sums of m and n terms are given by

Question 7.
The sum of n, 2_n, 3_n terms of a_n AP are s₁, s₂, and s₃ respectively. Prove that s₃ = 3(s₂ – s₁).
Solution:
Let a be the first term and d be the common difference of the AP

Question 8.
If a², b², c², are in AP, prove that \(\frac{a}{b+c}, \frac{b}{c+a}, \frac{c}{a+b}\) are in AP.
Solution:
since a², b², c², are in AP …(i)

Value-Based Questions in Science for Class 10: Provided 10th Class Science CBSE Value Based Questions are free to download from this page. We have jotted down the class 10 science NCERT value-based important question for all chapters to help you score high marks in the annual examination. These NCERT CBSE value-based questions on Science ace up your exam preparation & make you feel confident to attempt any type of examinations.

Chapter Wise Solved CBSE Value Based Questions for Class 10 Science

All important class 10 science topics solved questions are given in this CBSE Value Based Questions Solutions PDF. Download Free PDF Value Based Questions in Science for Class 10 by using the below given accessible quick links.

1. Value Based Questions on Chemical Reactions and Equations Class 10
2. Value Based Questions on Acids, Bases and Salts Class 10
3. Value Based Questions on Metals and Non-metals Class 10
4. Value Based Questions on Carbon and Its Compounds Class 10
5. Value Based Questions on Periodic Classification of Elements Class 10
6. Value Based Questions on Life Processes Class 10
7. Value Based Questions on Control and Coordination Class 10
8. Value Based Questions on How do Organisms Reproduce? Class 10
9. Value Based Questions on Heredity and Evolution Class 10
10. Value Based Questions on Light Reflection and Refraction Class 10
11. Value Based Questions on Human Eye and Colourful World Class 10
12. Value Based Questions on Electricity Class 10
13. Value Based Questions on Magnetic Effects of Electric Current Class 10
14. Value Based Questions on Sources of Energy Class 10
15. Value Based Questions on Our Environment Class 10
16. Value Based Questions on Management of Natural Resources Class 10

More Resources

• Extra Questions
• Value Based Questions in Science for Class 10
• HOTS Questions for Class 10 Science
• NCERT Solutions for Class 10 Science
• NCERT Exemplar Solutions for Class 10 Science
• Previous Year Question Papers for CBSE Class 10 Science

HOTS Questions for Class 10 Science: Higher-order Thinking Skills (HOTS) Questions are very important to practice during your final exam preparation. By practicing HOTS Questions for class 10 science, you can think creatively, and innovatively while answering the board exam papers. To assist students to familiarize with important topic and questions to be prepared for the upcoming board exam, we listed here a set of extra short & long questions with solutions for CBSE Class 10 Science Exam.

Class 10 Science NCERT HOTS Questions with Answers Free PDF

These important HOTS Questions are arranged in a systematic manner by referring to CBSE Class 10 Science previous year question paper, sample papers, etc. So, access the below links and download CBSE HOTS Questions & Answers in PDF format.

1. Hots Questions on Chemical Reactions and Equations
2. Hots Questions on Acids, Bases and Salts
3. Hots Questions on Metals and Non-metals
4. Hots Questions on Carbon and Its Compounds
5. Hots Questions on Periodic Classification of Elements
6. Hots Questions on Life Processes
7. Hots Questions on Control and Coordination
8. Hots Questions on How do Organisms Reproduce?
9. Hots Questions on Heredity and Evolution
10. Hots Questions on Light Reflection and Refraction
11. Hots Questions on Human Eye and Colourful World
12. Hots Questions on Electricity
13. Hots Questions on Magnetic Effects of Electric Current
14. Hots Questions on Sources of Energy
15. Hots Questions on Our Environment
16. Hots Questions on Management of Natural Resources

More Resources

• Extra Questions
• NCERT Solutions for Class 10 Science
• Value Based Questions in Science for Class 10
• NCERT Exemplar Solutions for Class 10 Science
• Previous Year Question Papers for CBSE Class 10 Science

If you have any doubts or questions regarding HOTS Questions for Class 10 Science, you can reach out to us in the comment section below and we will get back to you as soon as possible.