Here we are providing Triangles Class 10 Extra Questions Maths Chapter 6 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.
Extra Questions for Class 10 Maths Triangles with Answers Solutions
Extra Questions for Class 10 Maths Chapter 6 Triangles with Solutions Answers
Triangles Class 10 Extra Questions Very Short Answer Type
Question 1.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Solution:
Since the perimeters and two sides are proportional
∴ The third side is proportional to the corresponding third side.
i.e., The two triangles will be similar by SSS criterion.
Question 2.
A and B are respectively the points on the sides PQ and PR of a ∆PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm, and PB = 4 cm. Is AB || QR? Give reason.
Solution:
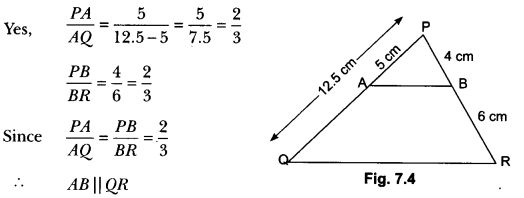
Question 3.
If ∆ABC ~ ∆QRP, \(\frac { ar(∆ABC) }{ ar(∆PQR) } \) = \(\frac{9}{4}\), AB = 18 cm and BC = 15 cm, then find the length of PR.
Solution:
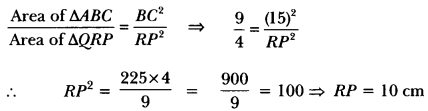
Question 4.
If it is given that ∆ABC ~ ∆PQR with \(\frac{BC}{QR}\) = \(\frac{1}{3}\), then find \(\frac { ar(∆PQR) }{ ar(∆ABC) } \)
Solution:
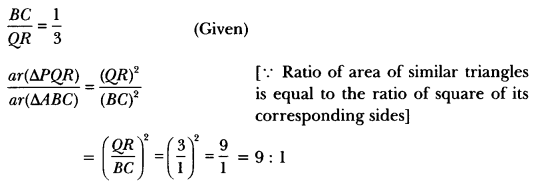
Question 5.
∆DEF ~ ∆ABC, if DE : AB = 2 : 3 and ar(∆DEF) is equal to 44 square units. Find the area (∆ABC).
Solution:

Question 6.
Is the triangle with sides 12 cm, 16 cm and 18 cm a right triangle? Give reason.
Solution:
Here, 122+ 162 = 144 + 256 = 400 ≠ 182
∴ The given triangle is not a right triangle.
Triangles Class 10 Extra Questions Short Answer Type 1
Question 1.
In triangles PQR and TSM, ∠P = 55°, ∠Q = 25°, ∠M = 100°, and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Solution:
Şince, ∠R = 180° – (∠P + ∠Q)
= 180° – (55° + 25°) = 100° = ∠M
∠Q = ∠S = 25° (Given)
∆QPR ~ ∆STM
i.e., . ∆QPR is not similar to ∆TSM.
Question 2.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 63°, then the measures of ∠C = 70°. Is it true? Give reason.
Solution:
Since ∆ABC ~ ∆DEF
∴ ∠A = ∠D = 47°
∠B = ∠E = 63°
∴ ∠C = 180° – (∠A + ∠B) = 180° – (47° + 63°) = 70°
∴ Given statement is true.
Question 3.
Let ∆ABC ~ ∆DEF and their areas be respectively 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution:
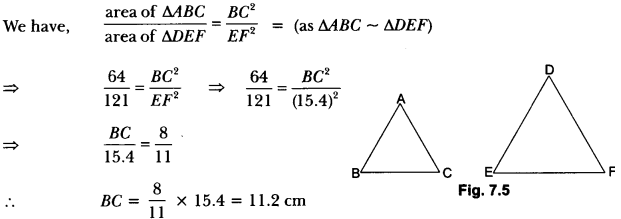
Question 4.
ABC is an isosceles triangle right-angled at C. Prove that AB2 = 2AC2.
Solution:
∆ABC is right-angled at C.
∴ AB2 = AC2 + BC2 [By Pythagoras theorem]
⇒ AB2 = AC2 + AC2
[∵ AC = BC]
⇒ AB2 = 2AC2
Question 5.
Sides of triangle are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
Solution:
(i) Let a = 7 cm, b = 24 cm and c = 25 cm.
Here, largest side, c = 25 cm
We have, a2 + b2 = (7)2 + (24)2 = 49 + 576 = 625 = c2 [∵c = 25]
So, the triangle is a right triangle.
Hence, c is the hypotenuse of right triangle.
(ii) Let a = 3 cm, b = 8 cm and c = 6 cm
Here, largest side, b = 8 cm
We have, a2 + c2 = (3)2 + (6)2 = 9 + 36 = 45 ≠ b2
So, the triangle is not a right triangle.
Question 6.
If triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm. Then find the length of EF.
Solution:
∆ABC ~ ∆DEF (Given)
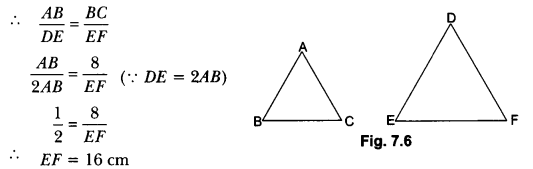
Question 7.
If the ratio of the perimeter of two similar triangles is 4 : 25, then find the ratio of the areas of the similar triangles.
Solution:
∵ Ratio of perimeter of 2 ∆’s = 4 : 25
∵ Ratio of corresponding sides of the two ∆’s = 4 : 25
Now, the ratio of area of 2 ∆’s = Ratio of square of its corresponding sides.
= \(\frac{(4)^{2}}{(25)^{2}}\) = \(\frac{16}{625}\)
Question 8.
In an isosceles ∆ABC, if AC = BC and AB2 = 2AC2, then find ∠C.
Solution:
AB2 = 2AC2 (Given)
AB2 = AC2 + AC2
AB2 = AC2 + BC2 (∵ AC = BC)
Hence AB is the hypotenuse and ∆ABC is a right angle A.
So, ∠C = 90°
Question 9.
The length of the diagonals of a rhombus are 16 cm and 12 cm. Find the length of side of the rhombus.
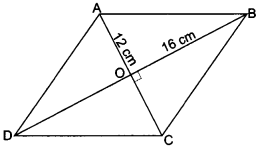
Solution:
∵ The diagonals of rhombus bisect each other at 90°.
∴ In the right angle ∆BOC
BO = 8 cm
CO = 6 cm
∴ By Pythagoras Theorem
BC2 = BO2 + CO2 = 64 + 36
BC2 = 100
BC = 10 cm
Question 10.
A man goes 24 m towards West and then 10 m towards North. How far is he from the starting point?
Solution:
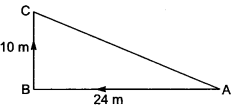
By Pythagoras Theorem
AC2 = AB2 + BC2 = (24)2 + (10)2
AC2 = 676
AC = 26 m
∴ The man is 26 m away from the starting point.
Question 11.
∆ABC ~ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, what is the perimeter of ∆ABC?
Solution:
Since ∆ABC ~ ∆DEF.

Question 12.
∆ABC ~ ∆PQR; if area of ∆ABC = 81 cm2, area of ∆PQR = 169 cm2 and AC = 7.2 cm, find the length of PR.
Solution:
Since ∆ABC ~ ∆PQR

Triangles Class 10 Extra Questions Short Answer Type 2
Question 1.
In Fig. 7.10, DE || BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x.
Solution:
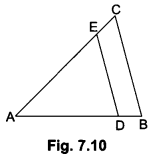
In ∆ABC, we have
DE || BC,
∴ \(\frac{A D}{D B}\) = \(\frac{A E}{E C}\) [By Basic Proportionality Theorem]
⇒ \(\frac{x}{x-2}\) = \(\frac{x+2}{x-1}\)
⇒ x(x – 1) = (x – 2) (x + 2)
⇒ x2 – x = x2 – 4
⇒ x = 4
Question 2.
E and F are points on the sides PQ and PR respectively of a ∆PQR. Show that EF ||QR if PQ = 1.28 cm, PR= 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
Solution:
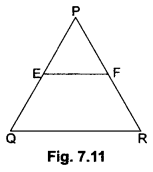
We have, PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm
Now, EQ = PQ-PE = 1.28 – 0.18 = 1.10 cm and
FR = PR – PF = 2.56 – 0.36 = 2.20 cm
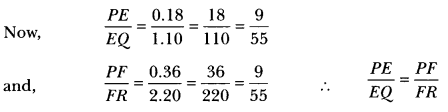
Therefore, EF || QR [By the converse of Basic Proportionality Theorem]
Question 3.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Let AB be a vertical pole of length 6m and BC be its shadow and DE be tower and EF be its shadow. Join AC and DF.
Now, in ∆ABC and ∆DEF, we have

h = 42 Hence, height of tower, DE = 42m
Question 4.
In Fig. 7.13, if LM || CB and LN || CD, prove that \(\frac{A M}{A B}=\frac{A N}{A D}\)
Solution:
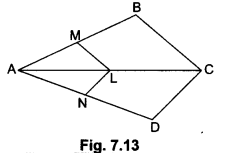
Firstly, in ∆ABC, we have
LM || CB (Given)
Therefore, by Basic Proportionality Theorem, we have


Question 5.
In Fig. 7.14, DE || OQ and DF || OR Show that EF || QR.
Solution:
In ΔPOQ, we have
DE || OQ (Given)

[Applying the converse of Basic Proportionality Theorem in ∆PQR]
Question 6.
Using converse of Basic Proportionality Theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution:
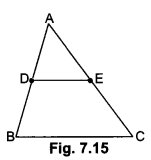
Given: ∆ABC in which D and E are the mid-points of sides AB and AC respectively.
To prove: DE || BC
Proof: Since D and E are the mid-points of AB and AC respectively
∴ AD = DB and AE = EC
DB EC Therefore, DE || BC (By the converse of Basic Proportionality Theorem)
Question 7.
State which pairs of triangles in the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form.

Solution:
(i) In ∆ABC and ∆QRP, we have
![]()

∆NML is not similar to ∆PQR.
Question 8.
In Fig. 7.17, \(\frac{A O}{O C}\) = \(\frac{B O}{O D}\) = \(\frac{1}{2}\) and AB = 5cm. Find the value of DC.
Solution:

⇒ DC = 10 cm.
Question 9.
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:
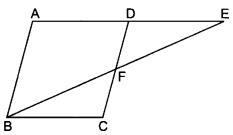
In ∆ABE and ∆CFB, we have
∠AEB = ∠CBF (Alternate angles)
∠A = ∠C (Opposite angles of a parallelogram)
∴ ∆ABE ~ ∆CFB (By AA criterion of similarity)
Question 10.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:
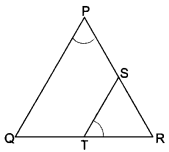
In ∆RPQ and ∆RTS, we have
∠RPQ = ∠RTS (Given)
∠PRQ = ∠TRS = ∠R (Common)
∴ ∆RPQ ~ ∆RTS (By AA criterion of similarity)
Question 11.
In Fig. 7.20, ABC and AMP are two right triangles right-angled at B and M respectively. Prove that:
(i) ∆ABC ~ ∆AMP
(ii) \(\frac{C A}{P A}\) = \(\frac{B C}{M P}\)
Solution:
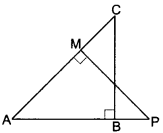
(i) In ∆ABC and ∆AMP, we have
∠ABC = ∠AMP = 90° (Given)
And, ∠BAC = ∠MAP (Common angle)
∴ ∆ABC ~ ∆AMP (By AA criterion of similarity)
(ii) As ∆ABC ~ ∆AMP (Proved above)
∴ \(\frac{C A}{P A}\) = \(\frac{B C}{M P}\) (Sides of similar triangles are proportional)
Question 12.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Solution:

Question 13.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:
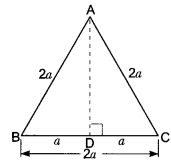
Let ABC be an equilateral triangle of side 2a units.
We draw AD ⊥ BC. Then D is the mid-point of BC.
⇒ \(\frac{B C}{2}\) = \(\frac{2 a}{2}\) = a
Now, ABD is a right triangle right-angled at D.
⇒ AB2 = AD2 + BD2 [By Pythagoras Theorem]
⇒ (2a)2 = AD2 + a2
⇒ AD2 = 4a2 – a2 = 3a2
⇒ AD = √3a
Hence, each altitude = √3a unit.
Question 14.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1 \(\frac{1}{2}\) hours?
Solution:
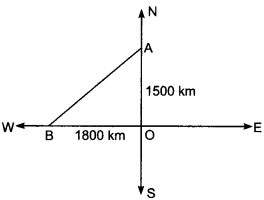
Let the first aeroplane starts from O and goes upto A towards north where
![]()
(Distance = Speed × Time)
Again let second aeroplane starts from O at the same time and goes upto B towards west where
OB = 1200 × \(\frac{3}{2}\) = 1800 km
Now, we have to find AB.
In right angled ∆ABO, we have
AB2 = OA2 + OB2 [By using Pythagoras Theorem]
⇒ AB2 = (1500)2 + (1800)2
⇒ AB2 = 2250000 + 3240000
⇒ AB2 = 5490000
∴ AB = 100 √549 = 100 × 23.4307 = 2343.07 km.
Question 15.
In the given Fig. 7.24, ∆ABC and ADBC are on the same base BC. If AD intersects BC at 0. Prove
that \(\frac { ar(∆ABC) }{ ar(∆DBC) }\) = \(\frac{AO}{DO}\)
Solution:
Given: ∆ABC and ∆DBC are on the same base BC and AD intersects BC at O.

Question 16.
In Fig. 7.25, AB || PQ || CD , AB = x units, CD = y units and PQ = z units. Prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\).
Solution:
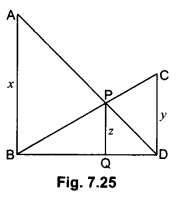
In ∆ADB and ∆PDQ,
Since AB || PQ
∠ABQ = ∠PQD (Corresponding ∠’s)
∠ADB = ∠PDQ (Common)
By AA-Similarity
ΔADB ~ ΔPDQ
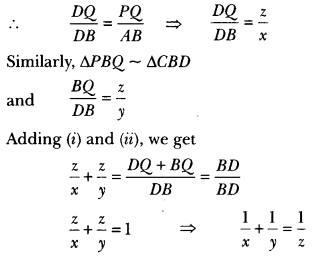
Question 17.
In Fig. 7.26, if ∆ABC ~ ∆DEF and their sides are of lengths (in cm) as marked along with them, then find the lengths of the sides of each triangle.
Solution:
∆ABC ~ ∆DEF (Given)
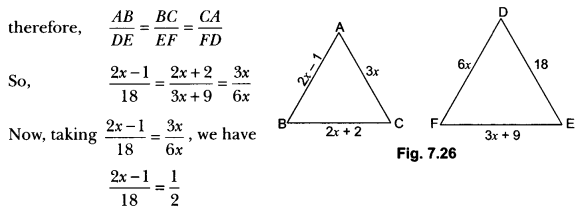
⇒ 4x – 2 = 18
⇒ x = 5
∴ AB = 2 × 5 – 1 = 9, BC = 2 × 5 + 2 = 12
CA = 3 × 5 = 15, DE = 18, EF = 3 × 5 + 9 = 24
and FD = 6 × 5 = 30
Hence, AB = 9 cm, BC = 12 cm, CA = 15 cm
DE = 18 cm, EF = 24 cm, FD = 30 cm
Question 18.
In ΔABC, it is given that \(\frac{A B}{A C}\) = \(\frac{B D}{D C}\) . If ∠B = 70° and ∠C = 50° then find ∠BAD.
Solution:
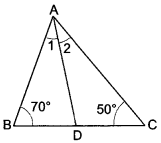
In ∆ABC
∵ ∠A + ∠B + 2C = 180° (Angle sum property)
∠A + 70° + 50° = 180°
⇒ ∠A = 180° – 120°
⇒ ∠A = 60°
∵ \(\frac{A B}{A C}\) = \(\frac{B D}{D C}\) (Given)
∴ ∠1 = ∠2
[Because if a line through one vertex of a triangle divides the opposite sides in the ratio of the other two sides, then the line bisects the angle at the vertex.]
But ∠1 + ∠2 = 60° …(ii)
From (i) and (ii) we get,
2∠1 = 60°
⇒ ∠1 = \(\frac{60°}{2}\) = 30°
Hence, ∠BAD = 30°
Question 19.
If the diagonals of a quadrilateral divide each other proportionally, prove that it is a trapezium.
Solution:

AB || DC
⇒ In quad ABCD, AB || DC
⇒ ABCD is a trapezium.
Question 20.
In the given Fig. 7.29, \(\frac{P S}{S Q}\) = \(\frac{P T}{T R}\) and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
Solution:
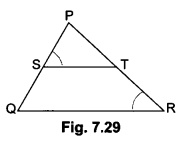
Given: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\) and ∠PST = ∠PRQ
To Prove: PQR is isosceles triangle.
Proof: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\)
By converse of BPT we get
ST || QR
∴ ∠PST = ∠PQR (Corresponding angles) ….(i)
But, ∠PST = ∠PRQ (Given) ….(ii)
From equation (i) and (ii)
∠PQR = ∠PRQ
⇒ PR = PQ
So, ∆PQR is an isosceles triangle.
Question 21.
The diagonals of a trapezium ABCD in which AB || DC, intersect at O. If AB = 2CD, then find the ratio of areas of triangles AOB and COD.
Solution:
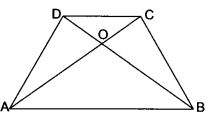
In ∆AOB and ∆COD
∠COD = ∠AOB (Vertically opposite angles)
∠CAB = ∠DCA (Alternate angles)
∆AOB ~ ∆COD (By AA-Similarity)
By area theorem
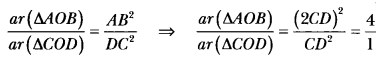
Hence, ar(∆AOB) : ar(∆COD) = 4 : 1.
Question 22.
In the given Fig. 7.31, find the value of x in terms of a, b and c.
Solution:
In ∆LMK and ∆PNK
We have, ∠M = ∠N = 50° and ∠K = ∠K (Common)
∴ ∆LMK ~ ∆PNK (AA – Similarity)
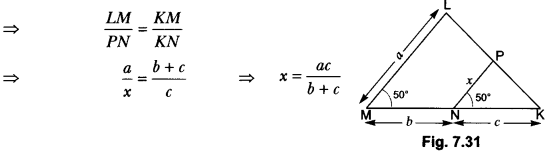
Question 23.
In the given Fig. 7.32, CD || LA and DE || AC. Find the length of CL, if BE = 4 cm and EC = 2 cm.
Solution:
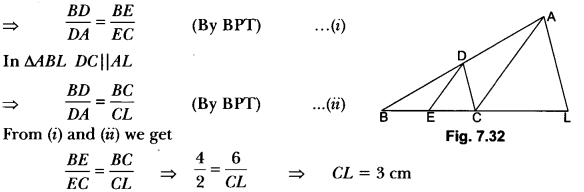
Question 24.
In the given Fig. 7.33, AB = AC. E is a point on CB produced. If AD is perpendicular to BC and EF perpendicular to AC, prove that ∆ABD is similar to ∆ECF.
Solution:
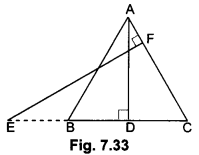
AB = AC (Given)
⇒ ∠ABC = ∠ACB (Equal sides have equal opposite angles)
Now, in ∆ABD and ∆ECF
∠ABD = ∠ECF (Proved above)
∠ADB = ∠EFC (Each 90°)
So, ∆ABD ~ ∆ECF (AA – Similarity)
Triangles Class 10 Extra Questions Long Answer Type
Question 1.
Using Basic Proportionality Theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Solution:
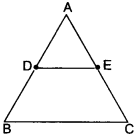
Given: A ∆ABC in which D is the mid-point of AB and DE is drawn parallel to BC, which meets AC at E.
To prove: AE = EC
Proof: In ∆ABC, DE || BC
∴ By Basic Proportionality Theorem, we have
\(\frac{A D}{D B}\) = \(\frac{A E}{E C}\) …(i)
Now, since D is the mid-point of AB
⇒ AD = BD …(ii)
From (i) and (ii), we have
\(\frac{A D}{D B}\) = \(\frac{A E}{E C}\)
⇒ 1 = \(\frac{A E}{E C}\)
Hence, E is the mid-point of AC.
Question 2.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{A O}{B O}\) = \(\frac{C O}{D O}\).
Solution:
Given: ABCD is a trapezium, in which AB || DC and its diagonals intersect each other at point O.

Question 3.
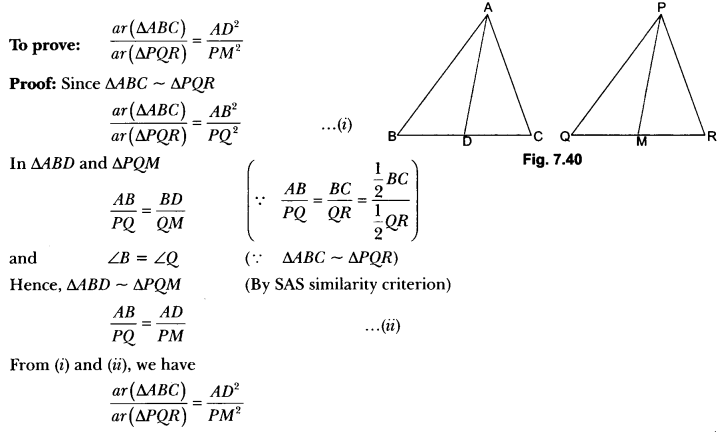
If AD and PM are medians of triangles ABC and PQR respectively, where ∆ABC ~ ∆PQR, prove that \(\frac{A B}{P Q}\) = \(\frac{A D}{P M}\)
Solution:
In ΔABD and ΔPQM we have
∠B = ∠Q (∵ ∆ABC ~ ∆PQR) …(i)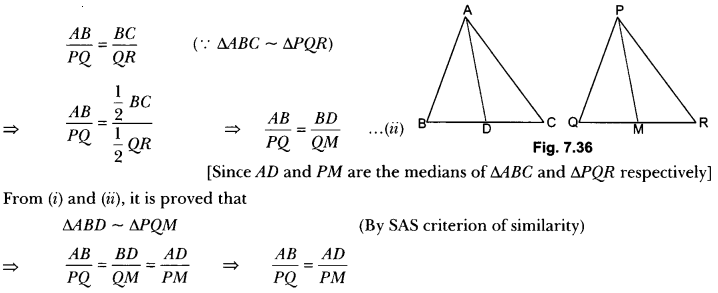
Question 4.
In Fig. 7.37, ABCD is a trapezium with AB || DC. If ∆AED is similar to ΔBEC, prove that AD = BC.
Solution:
In ∆EDC and ∆EBA we have
∠1 = ∠2 [Alternate angles]
∠3 = ∠4 [Alternate angles]
∠CED = ∠AEB [Vertically opposite angles]
∴ ∆EDC ~ ∆EBA [By AA criterion of similarity]
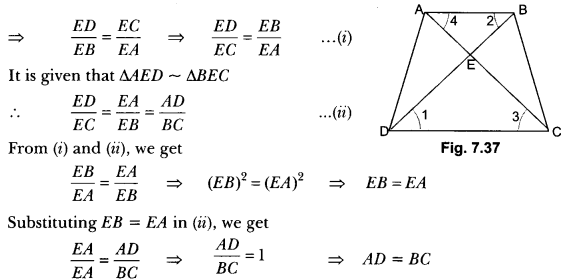
Question 5.
Prove that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.
Solution:
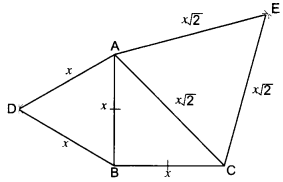
Given: A ∆ABC in which ∠ABC = 90° and AB = BC.
∆ABD and ΔCAE are equilateral triangles.
To Prove: ar(∆ABD) = \(\frac {1}{2}\) × ar(∆CAE)
Proof: Let AB = BC = x units.
∴ hyp. CA = √x2 + √x2 = x√2 units.
Each of the ABD and ∆CAE being equilateral has each angle equal to 60°.
∴ ∆АВD ~ ∆CAE
But, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Question 6.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
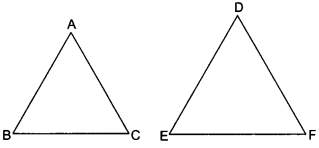
Given: Two triangles ABC and DEF, such that
∆ABC ~ ∆DEF and area (∆ABC) = area (∆DEF)
To prove: ∆ABC ≅ ∆DEF
Proof: ∆ABC ~ ∆DEF
⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
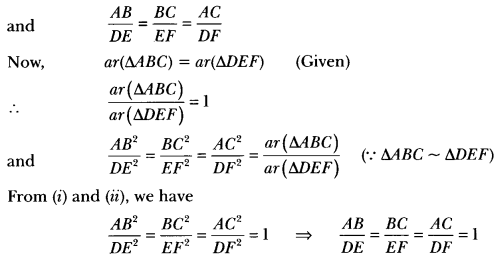
AB = DE, BC = EF, AC = DF
∆ABC ≅ ∆DEF (By SSS criterion of congruency)
Question 7.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
Let ∆ABC and ∆PQR be two similar triangles. AD and PM are the medians of ∆ABC and ∆PQR respectively.
Question 8.
In Fig. 7.41,0 is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Solution:
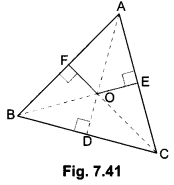
Join OA, OB and OC.
(i) In right ∆’s OFA, ODB and OEC, we have
OA2 = AF2 + OF2 …(i)
OB2 = BD2 + OD2 …(ii)
and C2 = CE2 + OE2
Adding (i), (ii) and (iii), we have
⇒ 0A2 + OB2 + OC2 = AF2 + BD2 + CE2 + OF2 + OD2 + OE2
⇒ 0A2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) We have, OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
⇒ (OA2 – OE2) + (OB2 – OF2) – (OC2 – OD2) = AF2 + BD2 + CE2
⇒ AE2 + CD2 + BF2 = AP2 + BD2 + CE2
[Using Pythagoras Theorem in ∆AOE, ∆BOF and ∆COD]
Question 9.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see Fig. 7.42). Prove that 2AB2 = 2AC2 + BC2
Solution:
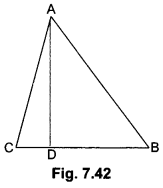
We have, DB = 3CD
Now,
BC = BD + CD
⇒ BC = 3CD + CD = 4CD (Given DB = 3CD)
∴ CD = \(\frac{1}{4}\) BC
and DB = 3CD = \(\frac{1}{4}\)BC
Now, in right-angled triangle ABD using Pythagoras Theorem we have
AB2 = AD2 + DB2 …(i)
Again, in right-angled triangle ∆ADC, we have
AC2 = AD2 + CD2 …(ii)
Subtracting (ii) from (i), we have
AB2 – AC2 = DB2 – CD2
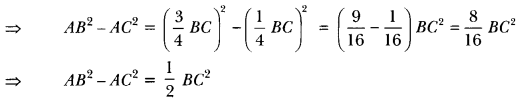
∴ 2AB2 – 2AC2 = BC2
⇒ 2AB2 = 2AC2 + BC2
Question 10.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:
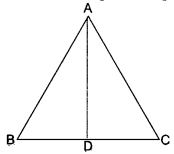
Let ABC be an equilateral triangle and let AD ⊥ BC.
∴ BD = DC
Now, in right-angled triangle ADB, we have
AB2 = AD2 + BD2 [Using Pythagoras Theorem]
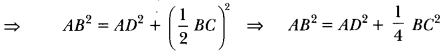
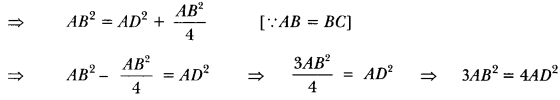
Question 11.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7.44 DE || BC and BD = CE. Prove that ∆ABC is an isosceles triangle.
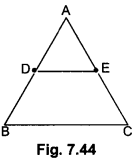
Solution:
Given: A triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively.

⇒ AB = AC (As DB = EC)
∴ ∆ABC is an isosceles triangle.
Question 12.
In Fig. 7.46, ABD is a triangle right-angled at A and AC ⊥ BD Show that
(i) AB2 = BC. BD
(ii) AD2 = BD.CD
(iii) AC2 = BC.DC
Solution:
Given: ABD is a triangle right-angled at A and AC ⊥ BD.
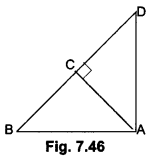
To prove: (i) AB2 = BC .BD
(ii) AD2 = BD.CD
(iii) AC2 = BC . DC
Proof: (i) In ∆ACB and ∆DAB, we have
∠ACB = ∠DAB = 90°
∠ABC = ∠DBA = ∠B [Common]
∴ ∆ACB ~ ∆DAB [By AA criterion of similarity]
\(\frac{BC}{AB}=\frac{AB}{DB}\)
⇒ AB2 = BC.BD
(ii) In ∆ACD and ∆BAD, we have
∠ACD = ∠BAD = 90°
∠CDA = ∠BDA = ∠D [Common]
∴ ∆ACD ~ ∆BAD [By AA criterion of similarity]
\(\frac{AD}{BD}=\frac{CD}{AD}\)
⇒ AD2 = BD.CD
(iii) We have ∆ACB – ∆DAB
⇒ ∆ВСА ~ ∆ВAD …(i)
and ∆ACD ~ ∆BAD …(ii)
From (i) and (ii), we have
∆ВСА ~ ∆АСD
\(\frac{B C}{A C}=\frac{A C}{D C}\)
AC2 = BC . DC
Question 13.
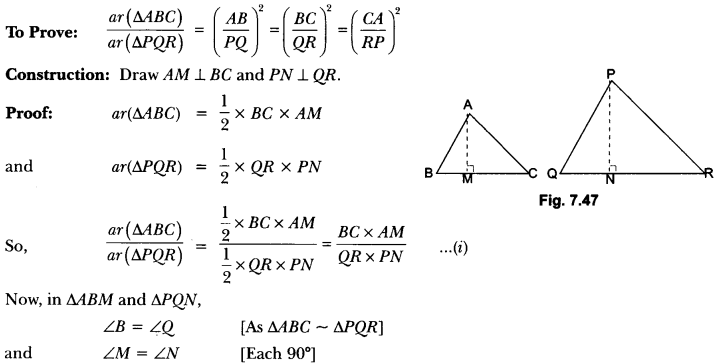
Prove that ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. Using the above result do the following: Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:
Given: Two triangles ABC and PQR such that ∆ABC ~ ∆PQR

Second Part:
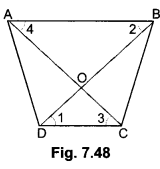
In ∆AOB and ∆COD we have
∠AOB = ∠COD (Vertically opposite angles) and
∠OAB = ∠OCD (Alternate angles)
∆AOB ~ ∆COD (By AA criterion of similarity]

Hence, the ratio of areas of ∆AOB and ∆COD 4 : 1.
Question 14.
Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Using the above, do the following:
Prove that, in a ∆ABC if AD is perpendicular to BC, then AB2 + CD2 = AC2 + BD2.
Solution:
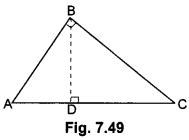
Given: A right triangle ABC right-angled at B.
To Prove: AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC
Proof: In ∆ADB and ∆ABC
∠A = ∠A (Common)
∠ADB = ∠ABC (Both 90°)
∴ ∆ADB ~ ∆ABC (AA similarity criterion)

Adding (i) and (ii), we get
AD. AC + CD . AC = AB2 + BC2
or, AC (AD + CD) = AB2 + BC2
or, AC . AC = AB2 + BC2
or, AC2 = AB2 +BC2
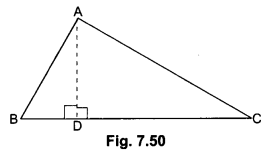
Second Part:
In Fig. 7.50, As AD ⊥ BC
Therefore, ∠ADB = ∠ADC = 90°
By Pythagoras Theorem, we have
AB2 = AD2 + BD2 …..(i)
AC2 = AD2 + DC2 …..(ii)
Subtracting (ii) from (i)
AB2 – AC2 = AD2 + BD2 – (AD2 + DC2)
⇒ AB2 – AC2 = BD2 – DC2 = AB2 + DC2 = BD2 + AC2
Question 15.
In a triangle, if the square on one side is equal to the sum of the squares on the other two sides, prove that the angle opposite to the first side is a right angle. Use the above theorem to find the measure of ∠PKR in Fig. 7.51.
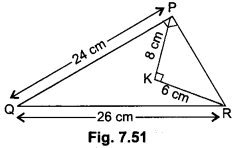
Solution:
Given: A triangle ABC in which AC2 = AB2 + BC2
To Prove: ∠B = 90°.
Construction: We construct a ∆PQR right-angled at Q such that PQ = AB and QR = BC
Proof: Now, from ∆PQR, we have,

Question 16.
ABC is a triangle in which AB = AC and D is a point on AC such that BC2 = AC × CD. Prove that BD = BC.
Solution:
Given: ∆ABC in which AB = AC and D is a point on the side AC such that BC2 = AC × CD
To prove: BD = BC
Construction: Join BD
Proof: We have,

Question 17.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
Let ABCD be a square and ABCE and ∆ACF have been drawn on side BC and the diagonal AC respectively.

Question 18.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.
Solution:
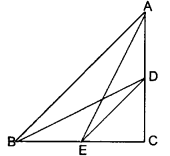
In right angled ΔACE and ΔDCB, we have
AE2 = AC2 + CE2 (Pythagoras Theorem) …(i)
and BD2 = DC2 + BC2… (ii)
Adding (i) and (ii), we have
AE2 + BD2 = AC2 + CE2 + DC2 + BC2
AE2 + BD2 = (AC2 + BC2) + (DC2 + CE2)
AE2 + BD2 = AB2 + DE2
[∵ AC2 + BC2 = AB2 in right-angled triangle ABC and DC2 + EC2 = DE2 in right-angled triangle CDE.]
Triangles Class 10 Extra Questions HOTS
Question 1.
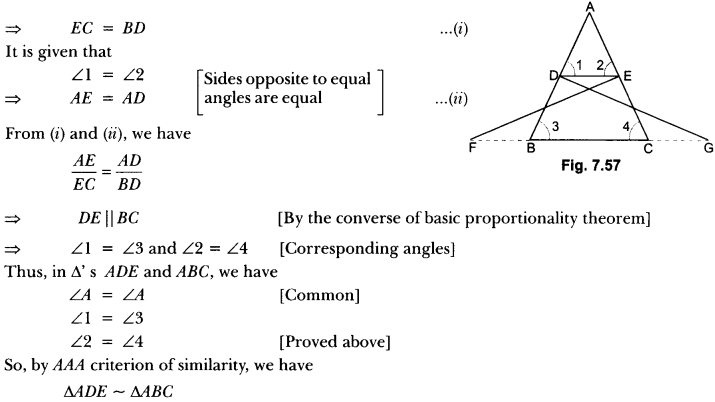
In Fig. 7.57, ΔFEC ≅ ΔGDB and ∠1 = ∠2. Prove that ΔADE ~ ∆ABC.
Solution:
Since ΔFEC ≅ ΔGDB
Question 2.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution:
Given: In ∆ABC and ∆PQR, AD and PM are their medians respectively
![]()
To prove: ∆ABC ~ ∆PQR
Construction: Produce AD to E such that AD = DE and produce PM to N such that PM = MN. Join BE, CE, QN, RN.
Proof: Quadrilateral ABEC and PQNR are ||gm because their diagonals bisect each other at D and M respectively.
⇒ BE = AC and QN = PR
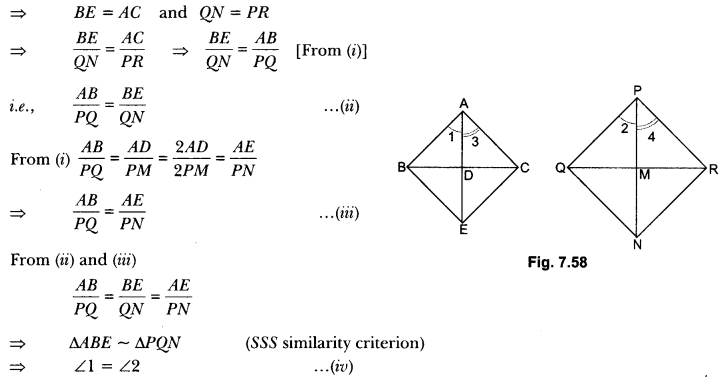
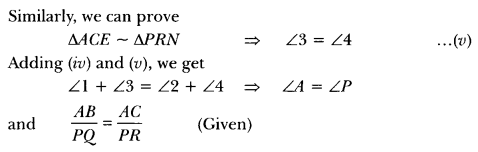
∆ABC ~ ∆PQR (By SAS criterion of similarity)
Question 3.
In Fig. 7.59, P is the mid-point of BC and Q is the mid-point of AP. If BQ when produced meets AC at R, prove that RA = \(\frac{1}{3}\) CA.
Solution:
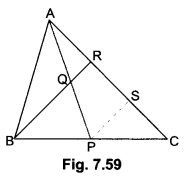
Given: In ∆ABC, P is the mid-point of BC, Q is the mid-point of AP such that BQ produced meets AC at R.
To prove: RA = \(\frac{1}{3}\) CA
Construction: Draw PS || BR, meeting AC at S.
Proof: In ABCR, P is the mid-point of BC and PS || BR.
∴ S is the mid-point of CR.
⇒ CS = SR ….(i)
In ∆APS, Q is the mid-point of AP and QR ||PS
∴ R is the mid-point of AS.
∴ AR = RS …(ii)
From (i) and (ii), we get
AR = RS = SC
⇒ AC = AR + RS + SC = 3 AR
⇒ AR = \(\frac{1}{3}\)AC = \(\frac{1}{3}\)CA
Question 4.
In Fig. 7.60, ABC and DBC are two triangles on the same base BC. If ar(∆ABC) AO AD intersects BC at O, show that \(\frac { ar(∆ABC) }{ ar(∆DBC) }\) = \(\frac{AO}{DO}\)
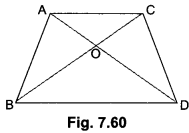
Solution:
Given: Two triangles ∆ABC and ADBC which stand on the same base but on opposite sides of BC.

Question 5.
Two poles of height a metres and b metres are p metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given \(\frac{a b}{a+b}\) metres.
Solution:
Let AB and CD be two poles of height a and b metres respectively such that the poles are p metres
apart i.e., AC = p metres.
Suppose the lines AD and BC meet at O such that OL = h metres.
Let CL = x and LA = y. Then, x + y = p.
In ∆ABC and ALOC, we have
∠CAB = ∠CLO [Each equal to 90°)
∠C = ∠C [Common]
∴ ∆ABC ~ ∆LOC [By AA criterion of similarity]
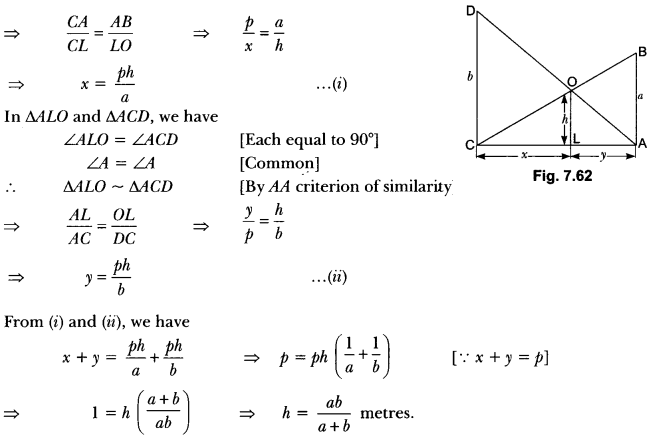
Hence, the height of the intersection of the lines joining the top of each pole to the foot of the opposite pole is \(\frac{a b}{a+b}\) metres.
Question 6.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\) BC. Prove that 9AD2 = 7AB2.
Solution:
Given: An equilateral triangle ABC and D be a point on BC such that
BD = \(\frac{1}{3}\) BC.
To Prove: 9AD2 = 7AB2
Construction: Draw AE ⊥ BC. Join AD.
DE Proof: ∆ABC is an equilateral triangle and AE ⊥ BC
BE = EC
Thus, we have
BD = \(\frac{1}{3}\) BC and DC = \(\frac{2}{3}\) BC and BE = EC = \(\frac{1}{2\) BC
In ∆AEB
AE2 + BE2 = AB2 [Using Pythagoras Theorem]
AE2 = AB2 – BE2
AD2 – DE2 = AB2 – BE2 [∵ In ∆AED, AD2 = AE2 + DE2]
AD2 = AB2 – BE2 + DE2
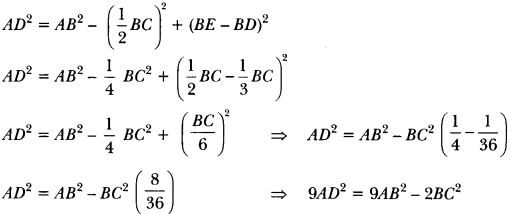
9AD2 = 9AB2 – 2AB2 [∵ AB = BC]
9AD2 = 7AB2
Question 7.
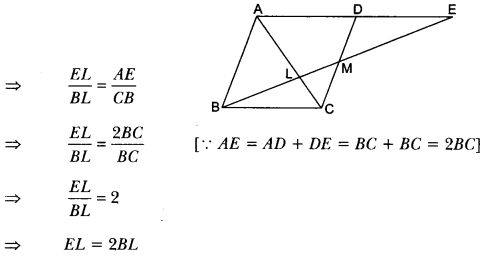
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced to E. Prove that EL = 2BL.
Solution:
In ∆BMC and ∆EMD, we have
MC = MD [∵ M is the mid-point of CD]
∠CMB = ∠DME [Vertically opposite angles]
and ∠MBC = ∠MED [Alternate angles]
So, by AAS criterion of congruence, we have
∆BMC ≅ ∆EMD
⇒ BC = DE [CPCT]
Also, BC = AD [∵ ABCD is a parallelogram]
Now, in ∆AEL and ∆CBL, we have
∠ALE = ∠CLB [Vertically opposite angles]
∠EAL = ∠BCL [Alternate angles]
So, by AA criterion of similarity of triangles, we have
∆AEL ~ ∆CBL