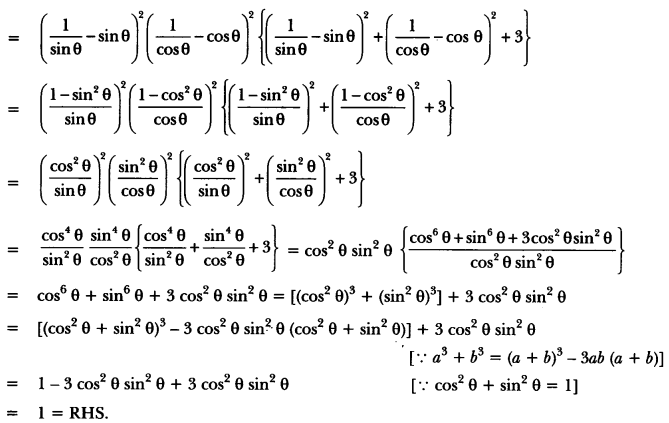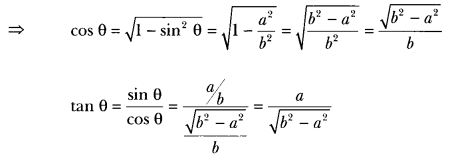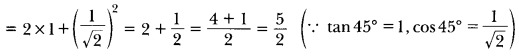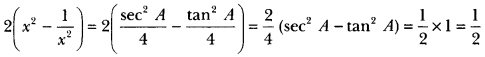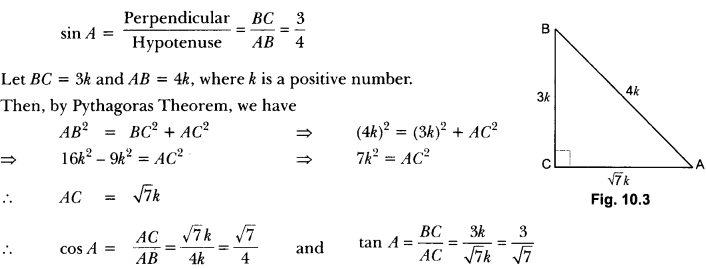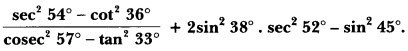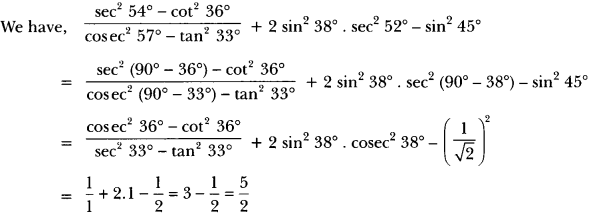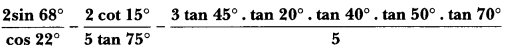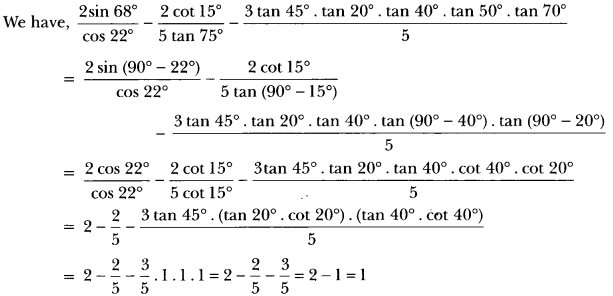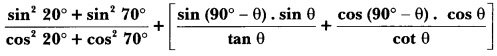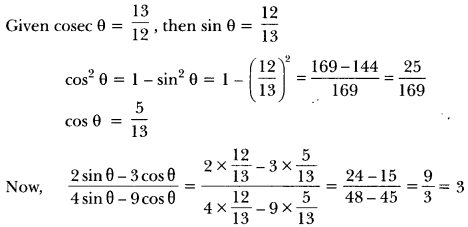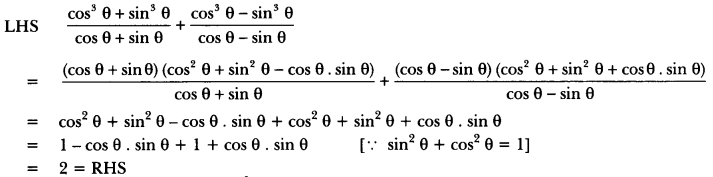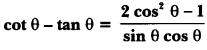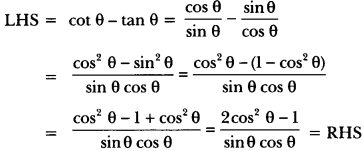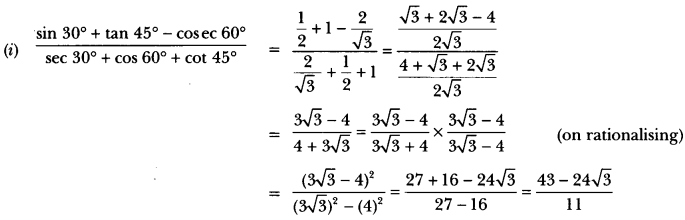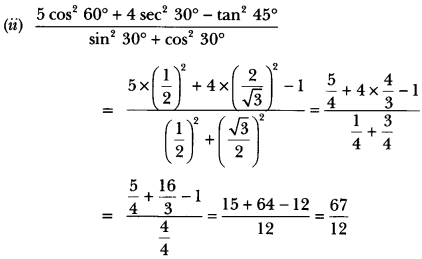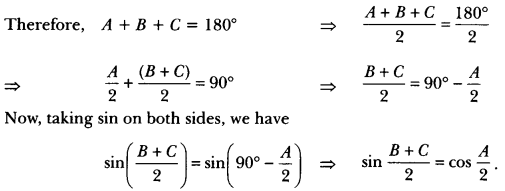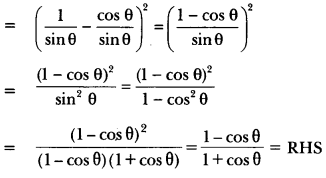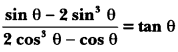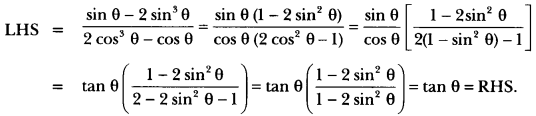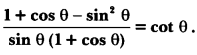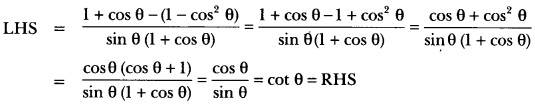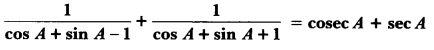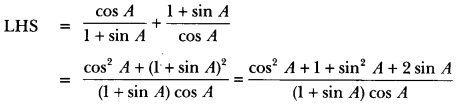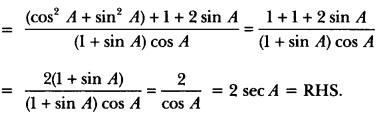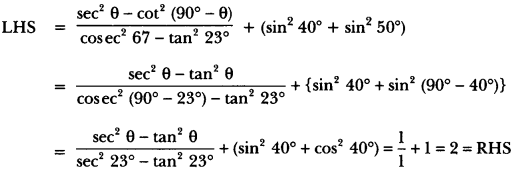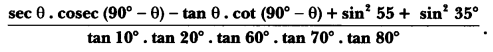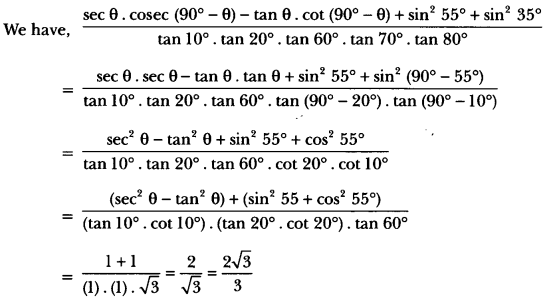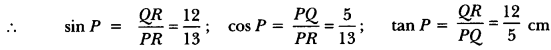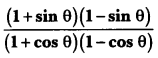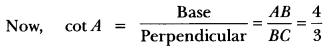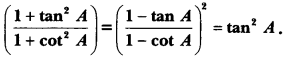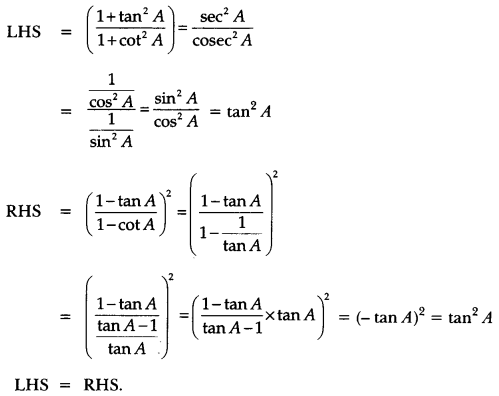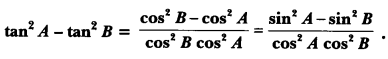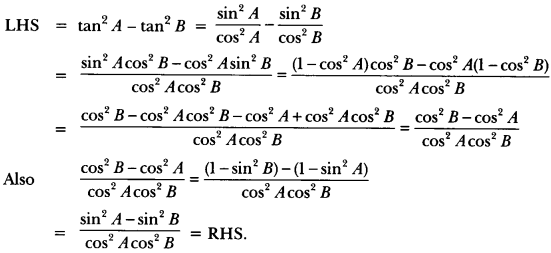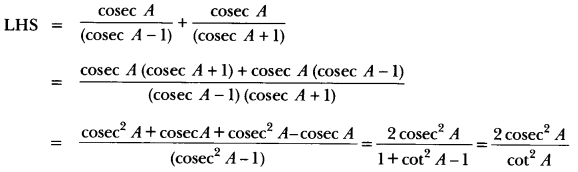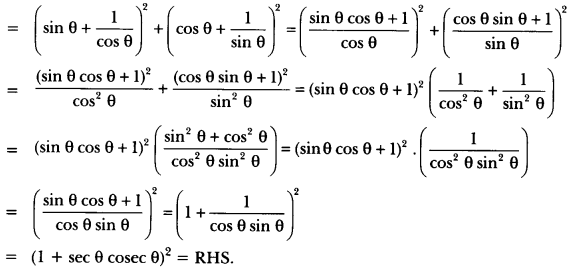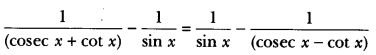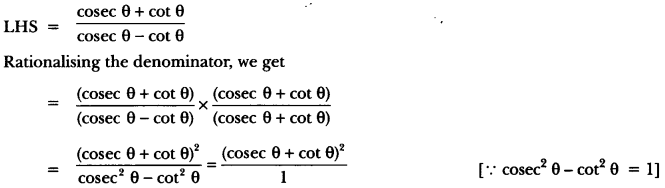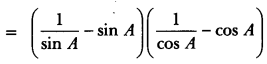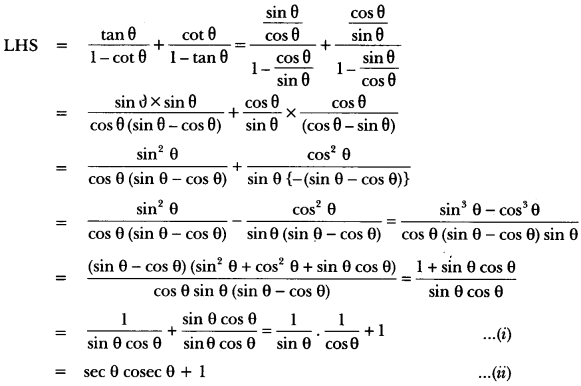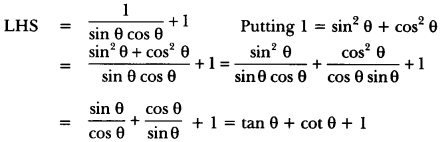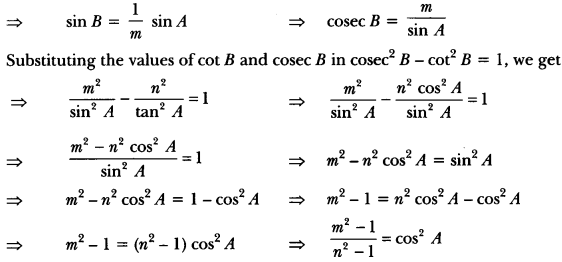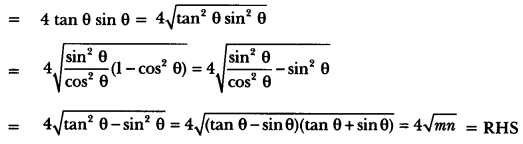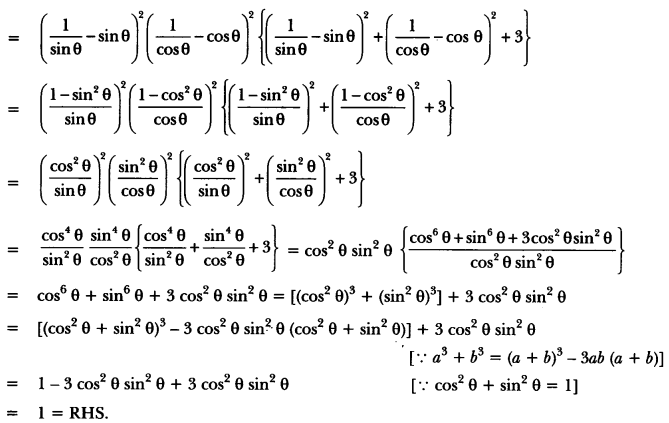Here we are providing Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.
Extra Questions for Class 10 Maths Introduction to Trigonometry with Answers Solutions
Extra Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry with Solutions Answers
Introduction to Trigonometry Class 10 Extra Questions Short Answer Type 1
Question 1.
Find maximum value of \(\frac{1}{\sec \theta}\), 0°≤ θ ≤ 90°.
Solution:
\(\frac{1}{\sec \theta}\), (0° ≤ θ ≤ 90°) (Given)
∵ sec θ is in the denominator
∴ The min. value of sec θ will return max. value for \(\frac{1}{\sec \theta}\).
But the min. value of sec θ is sec 0° = 1.
Hence, the max. value of \(\frac{1}{\sec 0^{\circ}}\) = \(\frac{1}{1}\) = 1
Question 2.
Given that sin θ = \(\frac{a}{b}\), find the value of tan θ.
Solution:
sin θ = \(\frac{a}{b}\)
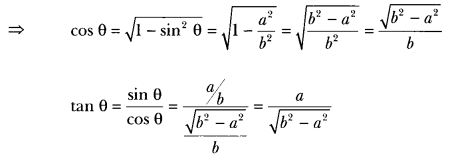
Question 3.
If sin θ = cos θ, then find the value of 2 tan θ + cos2 θ.
Solution:
sin θ = cos θ (Given)
It means value of θ = 45°
Now, 2 tan θ + cos2 θ = 2 tan 45° + cos2 45°
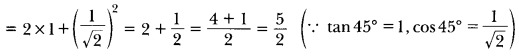
Question 4.
If sin (x – 20)° = cos (3x – 10)°, then find the value of x.
Solution:
sin (x – 20)° = cos (3x – 10)°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficient
90° – x° + 20° = 3x° – 10° = 110° + 10° = 3x° + x°
120° = 4x°
⇒ \(\frac{120^{\circ}}{4}\) = 30°
Question 5.
If sin2 A = \(\frac{1}{2}\)tan2 45°, where A is an acute angle, then find the value of A.
Solution:
sin2A = \(\frac{1}{2}\)tan2 45°
⇒ sin2A = \(\frac{1}{2}\) (1)2 [∵ tan 45° = 1]
= sin2 A = \(\frac{1}{2}\)
⇒ sin A = \(\frac{1}{\sqrt{2}}\)
Hence, ∠A = 45°
Question 6.
If x = a cos θ, y = b sin θ, then find the value of b2x2 + a2y2 – a2b2.
Solution:
Given x = acos θ, y = b sin θ
b2x2 + a2y2 – a2b2 = b2(acos θ)2 + a2(b sin θ)2 – a2b2
= a2b2 cos2θ + a2b2 sin2 θ – a2b2 = a2b2 (sin2 θ + cos2 θ) – a2b2
= a2b2 – a2b2 = θ (∵ sin2 θ + cos2 θ = 1)
Question 7.
If tan A = cot B, prove that A + B = 90°.
Solution: We have
tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°
Question 8.
If sec A = 2x and tan A = \(\frac{2}{x}\), find the value of 2\(\left(x^{2}-\frac{1}{x^{2}}\right)\) .
Solution:
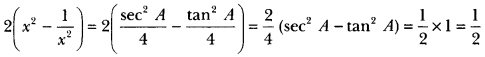
Question 9.
In a ∆ABC, if ∠C = 90°, prove that sin2 A + sin2 B = 1.
Solution:
Since ∠C = 90°
∴ ∠A + ∠B = 180° – ∠C = 90°
Now, sin2 A + sin2 B = sin2 A + sin2 (90° – A) = sin2 A + cos2 A = 1
Question 10.
If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.
Solution:
We have
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
∴ A = \(\frac{110}{5}\) = 22°
Introduction to Trigonometry Class 10 Extra Questions Short Answer Type 2
Question 1.
If sin A = \(\frac{3}{4}\), calculate cos A and tan A.
Solution:
Let us first draw a right ∆ABC in which ∠C = 90°.
Now, we know that
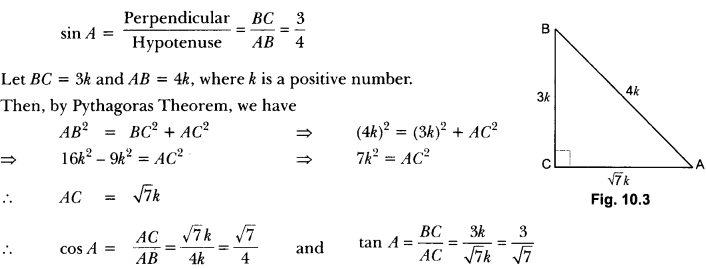
Question 2.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Let us first draw a right ∆ABC in which ∠B = 90°.
Now, we have, 15 cot A = 8

Question 3.
In Fig. 10.5, find tan P – cot R.
Solution:
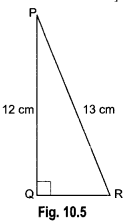
Using Pythagoras Theorem, we have
PR2 = PO2 + QR2
⇒ (13)2 = (12)2 + QR2
⇒ 169 = 144 + QR2
⇒ QR2 = 169 – 144 = 25
⇒ QR = 5 cm
Now, tan P = \(\frac{QR}{PQ}\) = \(\frac{5}{12}\) and cot R = \(\frac{QR}{PQ}\) = \(\frac{5}{12}\)
tan P – cot R = \(\frac{5}{12}\) – \(\frac{5}{12}\) = 0
Question 4.
If sin θ + cos θ = √3 , then prove that tan θ + cot θ = 1.
Solution:
sin θ + cos θ = √3
⇒ (sin θ + cos θ)2 = 3
⇒ sin2 θ + cos2 θ + 2 sin θ cos θ = 3
⇒ 2 sin cos θ = 2 (∵ sin2 θ + cos2 θ = 1)
⇒ sin θ. cos θ = 1 = sin2 θ + cos2 θ
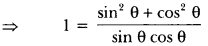
⇒ 1 = tan θ + cot θ = 1
Therefore tan θ + cot θ = 1
Question 5.
Prove that \(\frac { 1-sinθ }{ 1+sinθ } \) = (sec θ – tan θ)2
Solution:

Without using tables, evaluate the following (6 to 10).
Question 6.
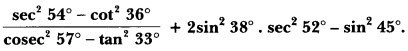
Solution:
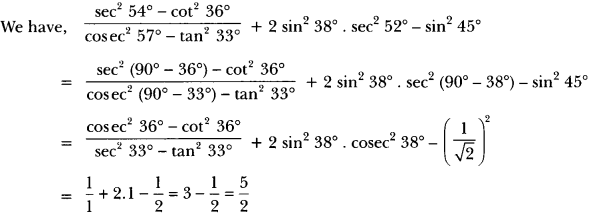
Question 7.
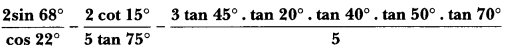
Solution:
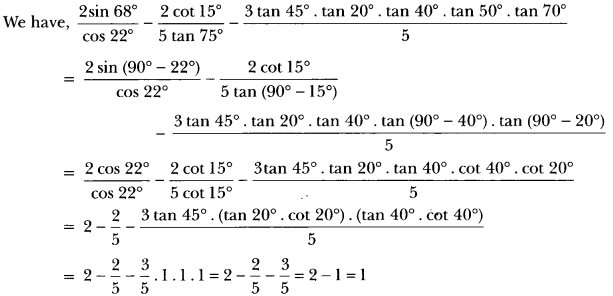
Question 8.
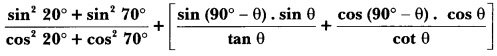
Solution:
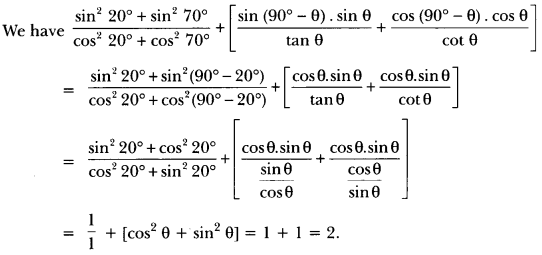
Question 9.
Evaluate: sin 25° cos 65° + cos 25° sin 65°.
Solution:
sin 25°. cos 65° + cos 25° . sin 65°
= sin (90° – 65°). cos 65° + cos (90° – 65°). sin 65°
= cos 65° . cos 65° + sin 65°. sin 65°
= cos2 65° + sin2 65° = 1.
Question 10.
Without using tables, evaluate the following:
3 cos 68°. cosec 22° – \(\frac{1}{2}\) tan 43°. tan 47°. tan 12°. tan 60°. tan 78°
Solution:
We have,
3 cos 68°. cosec 22° – \(\frac{1}{2}\) tan 43°. tan 47°. tan 12°. tan 60°. tan 78°.
= 3 cos (90° – 22°). cosec 22° – \(\frac{1}{2}\) . {tan 43° . tan (90° – 43°)}. {tan 12°. tan (90° – 12°). tan 60°}
= 3 sin 22°. cosec 22° – \(\frac{1}{2}\)(tan 43° . cot 43°). (tan 12°. cot 12°). tan 60°
= 3 × 1 – × 1 × 1 × √3 = 3 – \(\frac{\sqrt{3}}{2}\) = \(\frac{6-\sqrt{3}}{2}\).
Question 11.
If sin 30 = cos (θ – 6°) where 30 and (θ – 6°) are both acute angles, find the value of θ.
Solution:
According to question:
sin 3θ = cos (θ – 6°)
cos (90° – 30) = cos (θ – 6°) [∵ cos (90° – θ ) = sin θ]
90° – 3θ = θ – 6° [comparing the angles)
= 4θ = 90° + 6° = 96°
θ = \(\frac{96}{4}\) = 24°
Hence, θ = 24°
Question 12.
If sec θ = x + \(\frac{1}{4x}\), prove that sec θ + tan θ = 2x or \(\frac{1}{2x}\).
Solution:
Let sec θ + tan θ = λ …..(i)
We know that, sec2 θ – tan2 θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
⇒ λ(sec θ – tan θ) = 1
sec θ – tan θ = \(\frac{1}{\lambda}\) …..(ii)
Adding equations (i) and (ii), we get
Question 13.
Find an acute angle θ, when
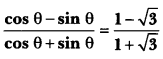
Solution:

On comparing we get
⇒ tan θ = √3
⇒ tan θ = tan 60°
= θ = 60°
Question 14.
The altitude AD of a MABC, in which ∠A is an obtuse angle has length 10 cm. If BD = 10 cm and CD = 10√3 cm, determine ∠A.
Solution:
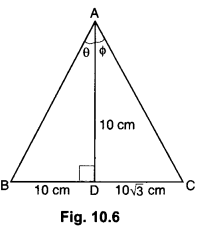
∆ABD is a right triangle right angled at D, such that AD = 10 cm and BD = 10 cm.
Let ∠BAD = θ
∴ tan θ = \(\frac{B D}{A D}\)
⇒ tan θ = \(\frac{10}{10}\) = 1
⇒ tan θ = tan 45°
⇒ θ = ∠BAD = 45° … (i)
∆ACD is a right triangle right angled at D such that AD = 10 cm and DC = 10√3 cm.
Let ∠CAD = Φ
∴ tan Φ = \(\frac{CD}{AD}\)
⇒ tan Φ = \(\frac{10 \sqrt{3}}{10}\) = √3
⇒ tan Φ = tan 60°
⇒ Φ = ∠CAD = 60°
From (i) & (ii), we have
∠BAC = ∠BAD + ∠CAD = 45° + 60° = 105°
Question 15.
If cosec θ = \(\frac{13}{12}\), evaluate \(\frac{2 \sin \theta-3 \cos \theta}{4 \sin \theta-9 \cos \theta}\)
Solution:
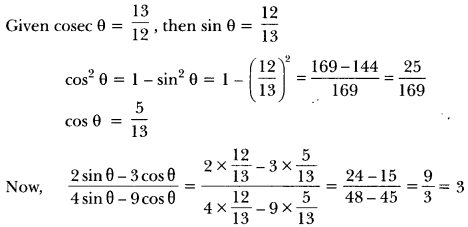
Question 16.
Prove that
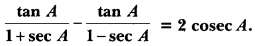
Solution:

Question 17.
Prove that
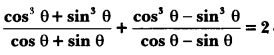
Solution:
We have,
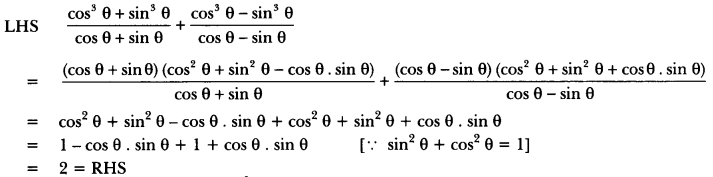
Question 18.
Prove that:
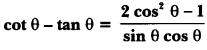
Solution:
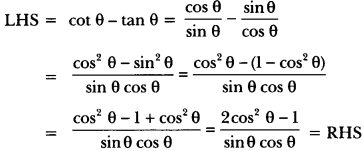
Question 19.
Prove that:
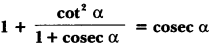
Solution:

Question 20.
Evaluate the following:
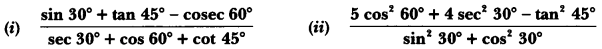
Solution:
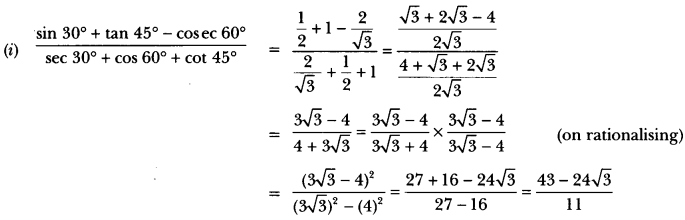
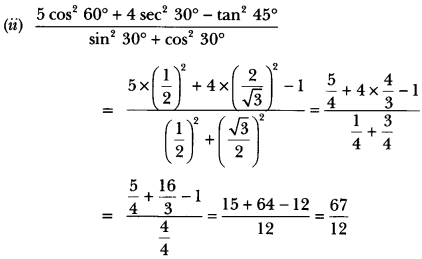
Question 21.
If tan (A +B) = √3 and tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° < A + B ≤ 90°; A > B, find A and B.
Solution:
We have, tan (A + B) = √3
⇒ tan (A + B) = tan 60°
∴ A + B = 60° …(i)
Again, tan (A – B) = \(\frac{1}{\sqrt{3}}\)
∴ A – B = 30° … (ii)
Adding (i) and (ii), we have
2A = 90°
⇒ A = 45°
Putting the value of A in (i), we have
45° + B = 60°
∴ B = 60° – 45o = 15°
Hence, A = 45° and B = 15°
Question 22.
If A, B and C are interior angles of a ∆ABC, then show that sin \(\left(\frac{B+C}{2}\right)\) = cos\(\frac{A}{2}\).
Solution:
Since A, B and C are the interior angles of a ∆ABC,
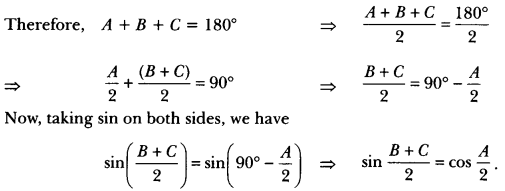
Question 23.
Prove that: (cosec θ – cot θ)2 = \(\frac {1-\cos\theta}{1+\cos\theta}\)
Solution:
LHS = (cosec θ – cot θ)2
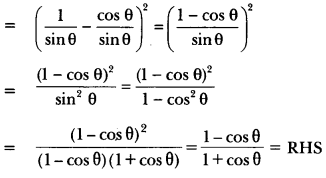
Question 24.
Prove that:
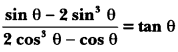
Solution:
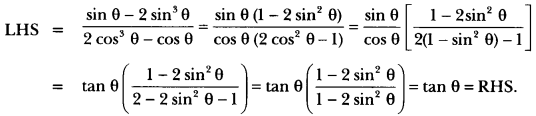
Question 25.
Prove that: (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2A.
Solution:
LHS = (sin A + cosec A)2 + (cos A + sec A)2
= sin2 A + coses2 A + 2sin A . cosec A + cos2 A + sec2 A + 2 cos A . sec A
= (sin2 A + coses2 A + 2) + (cos2 A + sec2 A + 2) [sin A. cosec A = 1]
= (sin2 A + cos2 A) + (coses2 A + sec2 A) + 4 [cos A. sec A = 1]
= 1 + 1 + cot2A + 1 + tan2 A + 4
= 7 + tan2 A + cot2 A = RHS [∵ 1 + cot2A = coses2 A and 1 + tan2 A = sec2 A]
Question 26.
Prove that:
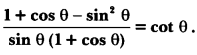
Solution:
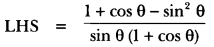
To obtain cot θ in RHS, we have to convert the numerator of LHS in cosine function and denominator in sine function.
Therefore converting sin2 θ = 1 – cos2 θ, we get
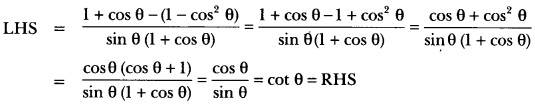
Question 27.
Prove that:
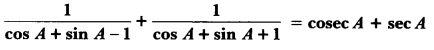
Solution:

Question 28.
Prove that:
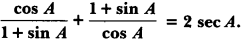
Solution:
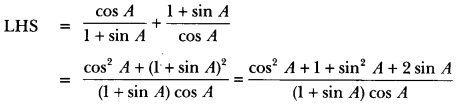
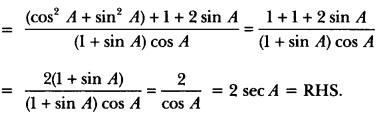
Question 29.
Without using trigonometric tables, prove that:
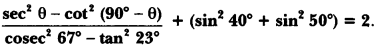
Solution:
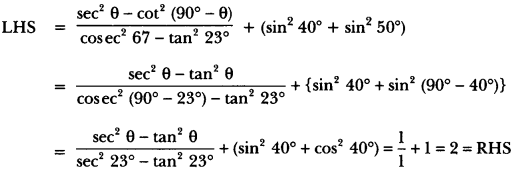
Question 30.
Evaluate:
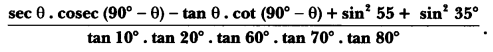
Solution:
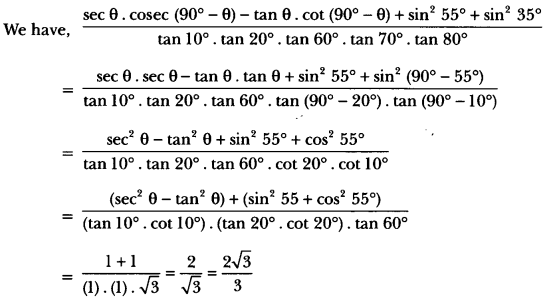
Introduction to Trigonometry Class 10 Extra Questions Long Answer Type
Question 1.
In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
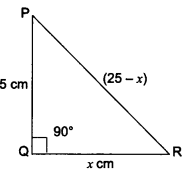
We have a right-angled ∆PQR in which ∠Q = 90°.
Let QR = x cm
Therefore, PR = (25 – x) cm
By Pythagoras Theorem, we have
PR2 = PQ2 + QR2
(25 – x)2 = 52 + x2
= (25 – x)2 – x2 = 25
(25 – x – x) (25 – x + x) = 25
(25 – 2x) 25 = 25
25 – 2x = 1
25 – 1 = 2x
= 24 = 2x
∴ x = 12 cm
Hence, QR = 12 cm
PR = (25 – x) cm = 25 – 12 = 13 cm
PQ = 5 cm
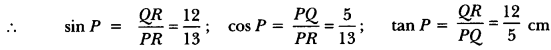
Question 2.
In triangle ABC right-angled at B, if tan A = \(\frac{1}{\sqrt{3}}\) find the value of:
(i) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C.
Solution:
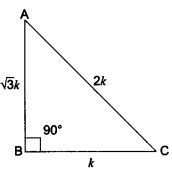
We have a right-angled ∆ABC in which ∠B = 90°.
and, tan A = \(\frac{1}{\sqrt{3}}\)
Now, tan A = \(\frac{1}{\sqrt{3}}\) = \(\frac{BC}{AB}\)
Let BC = k and AB = √3k
∴ By Pythagoras Theorem, we have
⇒ AC2 = AB2 + BC2
⇒ AC2 = (√3k)2 + (k)2 = 3k2 + k2
⇒ AC2 = 4k2

Question 3.
If cot θ = \(\frac{7}{8}\), evaluate:
(i)
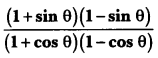
(ii) cot2 θ
Solution:
Let us draw a right triangle ABC in which ∠B = 90° and ∠C = θ.


Question 4.
If 3 cot A = 4, check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos2 A – sin2 A or not.
Solution:
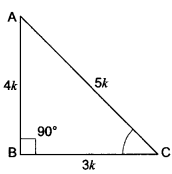
Let us consider a right triangle ABC in which ∠B = 90°
Let AB = 4k and BC = 3k
∴ By Pythagoras Theorem
AC2 = AB2 + BC2
AC = (4k)2 + (3k)2 = 16k2 + 9k2
AC2 = 25k2
∴ AC = 5k

Question 5.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
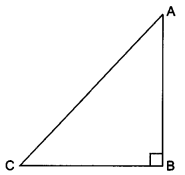
Let us consider a right-angled ∆ABC in which ∠B = 90°.
For ∠A we have

Question 6.
Prove that
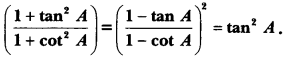
Solution:
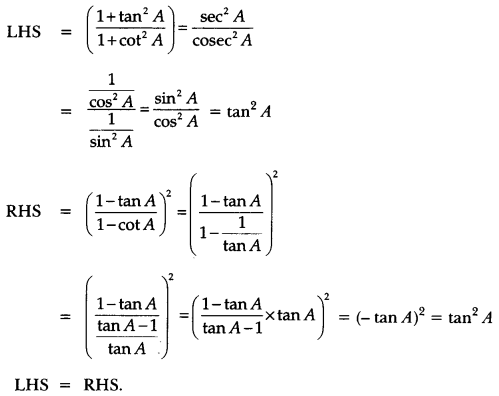
Question 7.
Prove that:
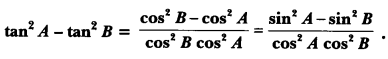
Solution:
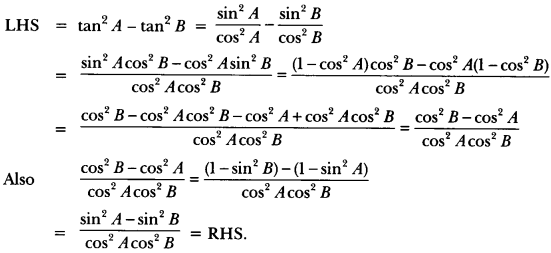
Question 8.
Prove that
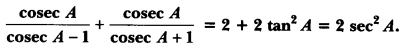
Solution:
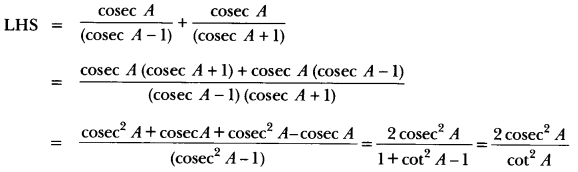
= 2 cosec2 A tan2 A = 2(1 + cot2 A). tan2 A
= 2 tan2 A + 2 tan2 A. cot2 A (∵ tan A cot A = 1)
= 2 + 2 tan2 A = 2(1 + tan2 A) = 2 sec2 A = RHS.
Question 9.
Prove that: (sin θ + sec θ)2 + (cos θ + cosec θ)2 = (1 + sec θ cosec θ)2.
Solution:
LHS = (sin θ + sec θ)2 + (cos θ + cosec θ)2
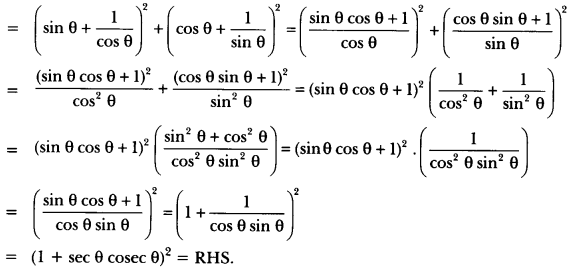
= (1 + sec θ cosec θ)2 = RHS.
Question 10.
Prove that:
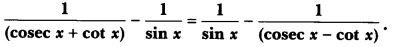
Solution:
In order to show that,
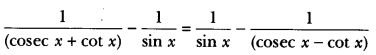

Question 11.
Prove that: \(\frac { cosecθ\quad +\quad cotθ }{ cosecθ\quad -\quad cotθ } \) = (cosec θ + cot θ) = 1 + 2 cot2 θ + 2 cosec θ cot θ.
Solution:
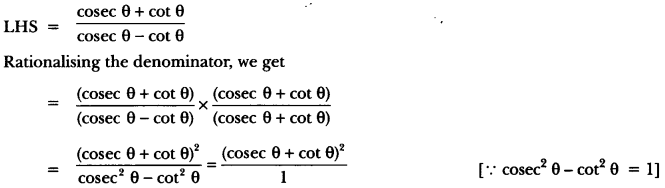
= cosec2 θ + cot2 θ + 2 cosec θ. cot θ
= (1 + cot2 θ) + cot2 θ + 2 cosec θ. cot θ
= 1 + 2 cot2 θ + 2 cosec . cot θ = RHS.
Question 12.
Prove that: 2 sec θ – sec θ – 2 cosec θ + cosec θ = cot – tan θ.
Solution:
LHS = 2 sec θ – sec θ – 2 cosec2 θ + cosec θ
= 2 (sec2 θ) – (sec2 θ)2 – 2 (cosec2 θ) + (cosec θ)2
= 2 (1 + tan2 θ) – (1 + tan4 θ)2 – 2(1 + cot2 θ) + (1 + cot2 θ)4
= 2 + 2 tan2 θ – (1 + 2 tan2 θ + tan2 θ) – 2 – 2 cot2 θ + (1 + 2 cot2 θ + cot θ) =
= 2 + 2 tan2 θ – 1 – 2 tan2 θ – tan4 θ – 2 – 2 cot2 θ + 1 + 2 cot4 θ + cot4 θ
= cot4 θ – tan4 θ = RHS
Question 13.
Prove that: (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\).
Solution:
LHS = (cosec A – sin A) (sec A – cos A)
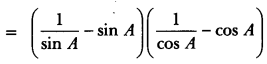

Introduction to Trigonometry Class 10 Extra Questions HOTS
Question 1.
Prove that:
\(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ = 1 + tan θ + cot θ.
Solution:
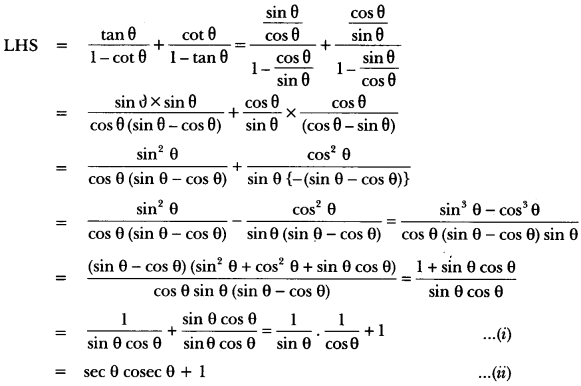
For second part
Now from (i), we have
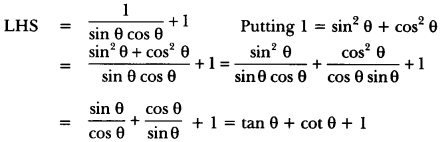
Question 2.
If tan A = n tan B and sin A = m sin B, prove that cos2 A = \(\frac{m^{2}-1}{n^{2}-1}\)
Solution:
We have to find cos2 A in terms of m and n. This means that the angle B is to be eliminated from
the given relations.
Now, tan A = n tan B
⇒ tan B = \(\frac{1}{n}\) tan A
⇒ cot B = \(\frac{n}{\tan A}\)
and
sin A = m sin B
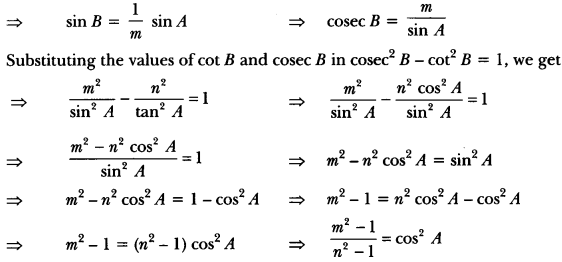
Question 3.
Prove the following identity, where the angle involved is acute angle for which the expressions are defined.
\(\frac { cosA-sinA+1 }{ cos A + sin A-1 } \) = cosec A + cot A, using the identity cosec2 A = 1 + cot2 A.
Solution:

= cosec A + cot A = RHS.
Question 4.
If x sin3 + y cos3 θ = sin θ cos θ and x sin θ = y cos θ, prove x2 + y2 = 1.
Solution:
We have, x sin3 + y cos3 θ = sin θ cos θ
⇒(x sin θ) sin2 θ + (y cos θ) cos2 θ sin θ cos θ
⇒ x sin θ (sin2 θ) + (x sin θ) cos2 = sin θ cos [∵ x sin θ = y cos θ]
⇒ x sin θ (sin2 θ + cos2 θ) = sin θ cos θ
⇒ x sin θ = sin θ cos
⇒ x = cos θ
Now, we have x sin θ = y cos θ
⇒ cos o sin θ = y cos θ [∵ x = cos θ]
⇒ y = sin θ
Hence, x2 + y2 = cos2 θ + sin2 θ = 1.
Question 5.
If tan θ + sin θ = m and tan θ – sin θ = n, show that (m2 – n2) = 4√mn.
Solution:
We have, given tan θ + sin θ = m, and tan θ – sin θ = n, then
LHS = (m2 – n2),= (tan θ + sin θ)2 – (tan θ – sin )2
= tan2 θ + sin2 θ + 2 tan θ sin θ – tan2 θ – sin2 θ + 2 tan θ sin θ
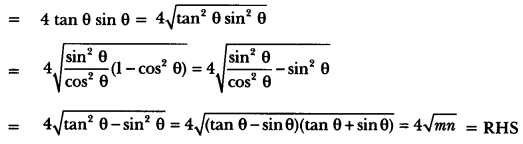
Question 6.
If cosec θ – sin θ = l and sec θ – cos θ = m, prove that l2 m2 (l2 + m2 + 3) = 1.
Solution:
LHS = l2 m2 (l2 + m2 + 3).
= (cosec θ – sin θ)2 (sec θ – cos θ)2 {(cosec θ – sin θ)2 + (sec θ – cos θ)2 + 3}