Dattu

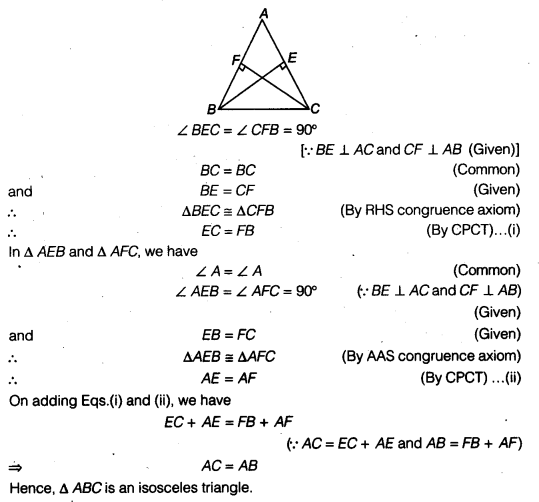
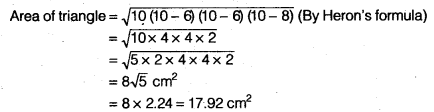NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1

NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1

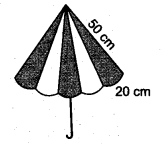
Question 1.
A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side a. Find the area of the signal board, using Heron’s formula.If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
We know that, an equilateral triangle has equal sides. So, all sides are equal to a.

Question 2.
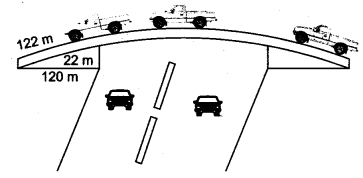
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?

Solution:
Leta = 122m,
b = 22m
c = 120m
We have, b² + c² = (22)² + (120)² = 484 + 14400 = 14884= (122)² = a²
Hence, the side walls are in right triangled shape.

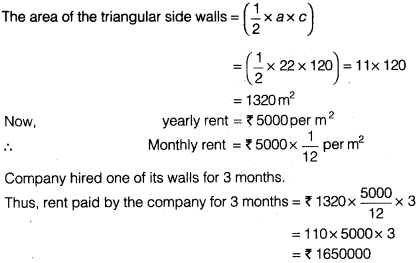
Question 3.
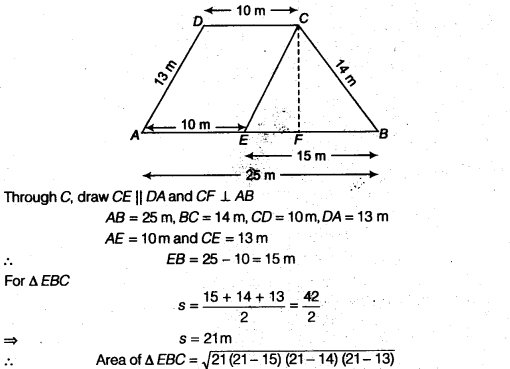
There is a slide in a park. One of its side Company hired one of its walls for 3 months.walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see figure). If the sides of the wall are 15 m, 11 m and 6m, find the area painted in colour.

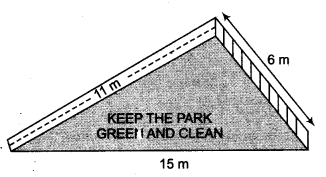
Solution:
The given figure formed a triangle whose sides are
a = 15m
b = 11m,
c = 6m

Question 4.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Solution Let the sides of a triangle, a = 18cm b = 10 cm and c
We have, perimeter = 42 cm

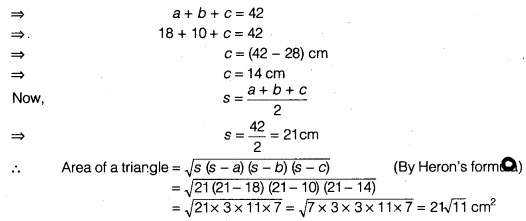
Question 5.
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Solution:
Suppose that the sides in cm, are 12x, 17x and 25x.
Then, we know that 12x + 17x + 25x = 540 (Perimeter of triangle)
⇒ 54x = 540
⇒ x=10
So, the sides of the triangle are 12 x 10 cm, 17 x 10 cm 25 x 10 cm
i.e., 120 cm, 170 cm, 250 cm

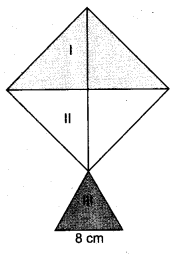
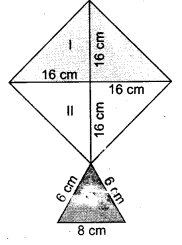
Question 6.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:

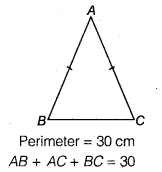
Let in isosceles ∆ ABC,
AB = AC = 12 cm (Given)

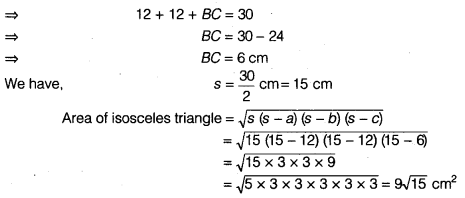
We hope the NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.2.

NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.2

Question 1.
A park, in the shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9m,BC = 12m,CD = 5m and AD = 8 m.
How much area does it occupy?
Solution:
In right ∆ BCD

Question 2.
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
Area of quadrilateral ABCD = Area of ∆ABC+ Area of ∆ACD

In ∆ ABC,
We have, AB = 3 cm, BC = 4 cm, CA = 5 cm
Therefore, AB² + BC² = 3² + 4² = 9 + 16 = 25 = (5)2 = CA²
Hence, ∆ ABC is a right triangle

Question 3.
Radha made a picture of an aeroplane with coloured paper as shown in figure. Find the total area of the paper used.

Solution:
For part I
It is a triangle with sides 5 cm, 5cm and 1cm

For part II
It is a rectangle with sides 6.5 cm and 1 cm
∴ Area of part II = 6.5 x 1
(∵ Area of rectangle = Length x Breadth)
= 6.5 cm2

For part III

Question 4.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram
Solution:
Let ABC be a triangle with sides
AB = 26 cm, BC = 28 cm, CA = 30 cm


We know that,
Area of parallelogram = Base x Height …(i)
We have,
Area of parallelogram = Area of ∆ ABC (Given)
= 336 cm²
From Eq. (i), we have
Base x Height = 336
⇒ 28 x Height = 336
⇒ Height = \(\frac { 336 }{ 28 }\)
⇒ Height =12cm

Question 5.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution:
Let ABCD be a rhombus.
Area of the rhombus ABCD = 2x area of ∆ ABD …(i)
(Since, in a rhombus diagonals divides two equal parts)

Question 6.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

Solution:
In an umbrella, each triangular piece is an isosceles triangle with sides 50 cm, 50 cm, 20 cm.

Since, there are 10 triangular piece, in those of them 5.5 are of different colours.
Hence, total area of cloth of each colour = 5 x 200√6 cm² = 1000√6 cm²

Question 7.
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in figure. How much paper of each shade has been used in it?

Solution:
Since, the kite is in the shape of a square

Each diagonal of square =32 cm (Given)
We know that, the diagonals of a square bisect each other at right angle.


Hence, paper of I colour has been used = 256 cm²
Paper of II colour has been used = 256 cm²
Paper of III colour has been used = 17.92 cm²

Question 8.
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see figure). Find the cost of polishing the tiles at the rate of 50 paise per cm .

Solution:
Given, the sides of a triangular tiles are 9 cm, 28 cm and 35 cm.
For each triangular tile, we have

Question 9.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution:
Here, ABCD is a trapezium and AB || DC.

We hope the NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.2 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 7 Heron’s Formula Ex 7.2, drop a comment below and we will get back to you at the earliest.