NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.5 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.5.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 11 |
| Chapter Name | Circles |
| Exercise | Ex 11.5 |
| Number of Questions Solved | 12 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.5
Question 1.
In figure A,B and C are three points on a circle with centre 0 such that ∠BOC = 30° and ∠ AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ ADC.
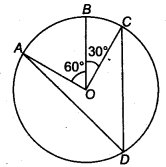
Solution:
∴ ∠AOC = ∠AOB + ∠BOC = 60P + 30° = 90°
∴ Arc ABC makes 90° at the centre of the circle.
∴ ∠ADC = \(\frac { 1 }{ 2 }\) ∠AOC
(∵ The angle subtended by an arc at the centre is double the angle subtended by it any part of the circle.)
= \(\frac { 1 }{ 2 }\) x 90° = 45°
Question 2.
A chord of a circle is equal to the radius of the circle, find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
Let BC be chord, which is equal to the radius. Join OB and OC.
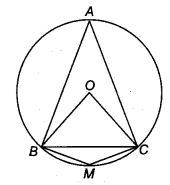
Given, BC=OB = OC
∴ ∆OBC is an equilateral triangle.
∠BOC =60°
∴ BAC = \(\frac { 1 }{ 2 }\) ∠BOC
= \(\frac { 1 }{ 2 }\) x 60° = 30°
(∵ The angle subtended by an arc at the centre is double the angle subtended by it any part of the circle.)
Here, ABMC is a cyclic quadrilateral.
∴ ∠BAC + ∠BMC = 180°
(∵ In a cyclic quadrilateral the sum of opposite angles is 180°)
⇒ ∠BMC= 180° – 30° =150°
Question 3.
In figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
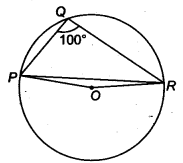
Solution:
∴ ∠POR = 2∠PQR = 2 x 100° = 200°
(Since, the angle subtended by the centre is double the angle subtended by circumference.)
Since, in ∆OPR, ∠POR = 360° – 200° = 160° .. (i)
Again, ∆ OPR, OP = OR (Radii of the circle)
∴ ∠OPR = ∠ORP (By property of isosceles triangle)
In ∆POR, ∠OPR + ∠ORP + ∠POR = 180° …(ii)
From Eqs. (i) and (ii), we get
∠OPR + ∠OPR + 160° = 180°
∴ 2 ∠OPR = 180° – 160° = 20°
∴ ∠OPR = \(\frac { { 120 }^{ circ } }{ 2 }\) = 10°
Question 4.
In figure, ∠ABC = 69°,∠ACB = 31°, find ∠BDC.
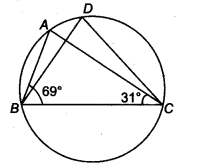
Solution:
∵ ∠BDC = ∠BAC …(i)
(Since, the angles in the same segment are equal)
Now , in ∆ABC
∴ ∠A + ∠B+ ∠C= 180°
⇒ ∠A+ 69°+ 31° = 180°
⇒ ∠A + 100° = 180°
∴ ∠A = 180° – 100° = 80°
⇒ ∠BAC=80°
∴ From Eq.(i)∠BDC = 80°
Question 5.
In figure, A, B and C are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠BAC.
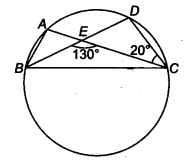
Solution:
∴ ∠AEB = 180° – 130° = 50° (Linear Pair) …(i)
⇒ ∠CED = ∠AEB = 50° (Vertically opposite)
Again ∠ABD = ∠ACD (Since, the angles in the same segment are equal)
∠ABE = ∠ECD
⇒ ∠ABE = 180° …(ii)
∴ In ∆ CDE
∠A+ 20° + 50° = 180° [From Eqs. (i) and (ii)]
∠A + 70° = 180°
∴ ∠A = 180°- 70° =110°
Hence ∠BAC = 110°
Question 6.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Solution:
Angles in the same segment are equal.
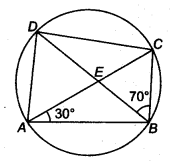
∴ ∠BDC = ∠BAC
∴ ∠BDC = 30°
In ∆ BCD, we have
∴ ∠BDC + ∠DBC + ∠BCD = 180° (Given, ∠DBC = 70° and ∠BDC = 30°)
∴ 30° + 70° + ∠BCD = 180°
∴ ∠BCD= 180°-30°-70° = 80°
If AB = BC, then ∠BCA = ∠BAC= 80° (Angles opposite to equal sides in a triangle are equal)
Now, ∠ECD = ∠BCD – ∠BCA = 80° – 30P = 50° (∵ ∠BCD = 80° and ∠BCA =30°)
Hence, ∠BCD = 80°
and ∠ECD = 50°
Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
Given: Diagonals NP and QM of a cyclic quadrilateral are diameters of the circle through the vertices M, P, Q and N of the quadrilateral NQPM.
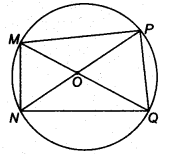
To prove: Quadrilateral NQPM is a rectangle.
Proof: ∵ ON = OP = OQ = OM (Radii of circle)
Now, ON = OP = \(\frac { 1 }{ 2 }\) NP
and OM = OQ = \(\frac { 1 }{ 2 }\) MQ
∴ NP = MQ
Hence, the diagonals of the quadrilateral MPQN are equal and bisect each other. So, quadrilateral NQPM is a rectangle.
Question 8.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:
Given: Non-parallel sides PS and QR of a trapezium PQRS are equal.
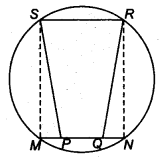
To prove: ABCD is a cyclic trapezium.
Construction: Draw SM ⊥ PQ and RN ⊥ PQ.
Proof In ∆SMP and ∆RNQ, we get
SP = RQ (Given)
∠SMP = ∠RNQ (Each = 90°)
and SM = RN
(∵ Distance between two parallel lines is always equal)
∴ By RHS criterion, we get
∆ SMP ≅ ∆ RNQ
So, ∠P = ∠Q (By CPCT)
and ∠PSM = ∠QRN
Now, ∠PSM = ∠QRN
∴ 90° + ∠PSM = 90° + ∠QRN (Adding both sides 90°)
∴ ∠MSR + ∠PSM = ∠NRS + ∠QRN (∵∠MSR = ∠NRS = 90°)
So, ∠PSR = ∠QRS
i.e., ∠S = ∠R
Thus, ∠P = ∠Q and ∠R = ∠S …(i)
∴ ∠P+ ∠Q+ ∠R+ ∠S = 360° (∵ Sum of the angles of a quadrilateral is 360°)
∴ 2∠S + ∠Q = 360° [From Eq. (i)]
∠S+∠O = 180°
Hence, PQRS is a cyclic trape∠ium.
Question 9.
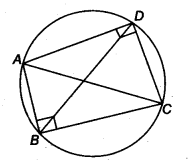
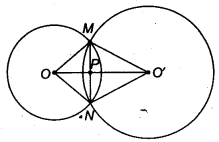
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A,D and P, Q respectively (see figure). Prove that ∠ ACP = ∠QCD.
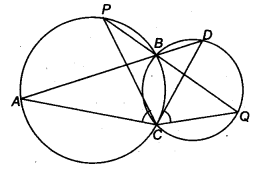
Solution:
Given: Two circles intersect at two points B and C. Through B two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q, respectively.
To prove: ∠ACP = ∠QCD
Proof: In circle I, ∠ACP = ∠ABP (Angles in the same segment) …(i)
In circle II, ∠QCD = ∠QBD{Angles in the same segment)…(ii)
∠ABP = ∠QBD (Vertically opposite angles)
From Eqs. (i) and (ii), we get ∠ACP = ∠QCD
Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution:
Given: Two circles are drawn with sides AC and AB of AABC as diameters . Both circles intersect each other at D.
To prove: D lies on BC.
Construction: Join AD.
Proof: Since, AC and AB are the diameters of the two circles.
∠ADB = 90° ( ∴ Angles in a semi-circle) …(i)
and ∠ADC = 90° (Angles in a semi-circle) …(ii)
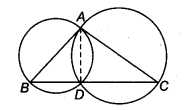
On adding Eqs. (i) and (ii), we get
∠ADB + ∠ADC = 90° + 90° = 180°
Hence, BCD is a straight line.
So, D lies on BC.
Question 11.
ABC and ADC are two right angled triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Solution:
Since, ∆ADC and ∆ABC are right angled triangles with common hypotenuse.
Draw a circle with AC as diameter passing through B and D. Join BD.
∵ Angles in the same segment are equal.
∴ ∠CBD = ∠CAD
Question 12.
Prove that a cyclic parallelogram is a rectangle.
Solution:
Given: PQRS is a parallelogram inscribed in a circle.
To prove: PQRS is a rectangle.
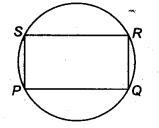
Proof: Since, PQRS is a cyclic quadrilateral.
∴ ∠P+∠R = 180°
(∵ Sum of opposite angles in a cyclic quadrilateral is 180°) …(i)
But ∠P = ∠R (∵ In a || gm opposite angles are equal) …(ii)
From Eqs. (i) and (ii), we get
∠P = ∠R = 90°
Similarly, ∠Q = ∠S = 90
∴ Each angle of PQRS is 90°.
Hence, PQRS is a rectangle.
We hope the NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.5, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.5, drop a comment below and we will get back to you at the earliest.


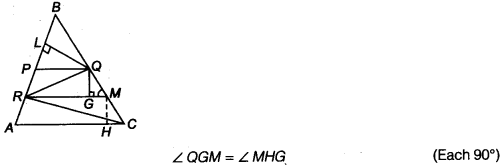
 src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>
src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>