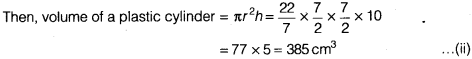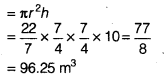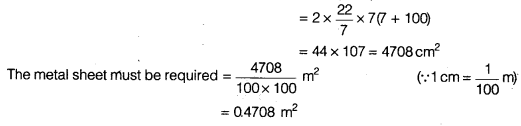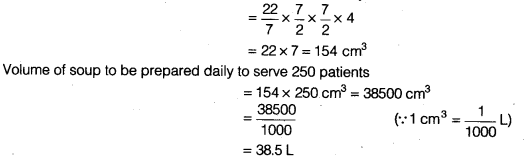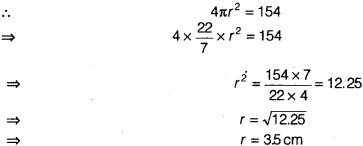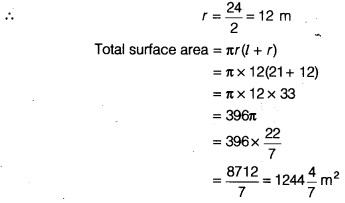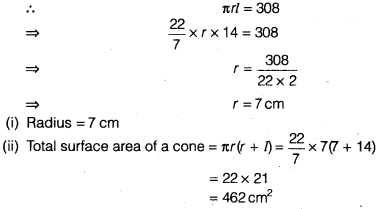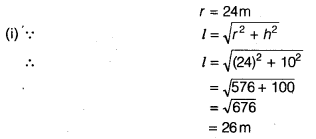Dattu

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7

Question 1.
Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
Solution:
(i) We have, r = 6 cm and h = 7cm

Question 2.
Find the capacity in litres of a conical vessel with
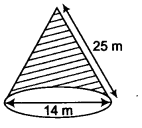
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
Solution:
(i) We have, r = 7 cm and l = 25 cm

Question 3.
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use π = 3.14)
Solution:

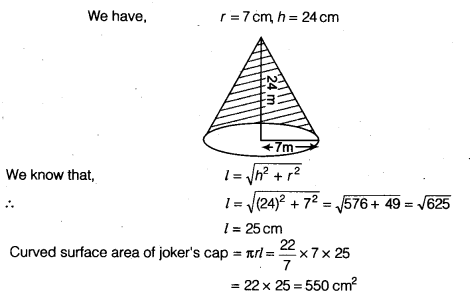
Question 4.
If the volume of a right circular cone of height 9 cm is 48 cm3, find the diameter of its base.
Solution:
We have, volume of a right circular cone = 48 π cm3

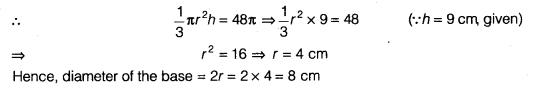
Question 5.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Solution:
We have, diameter = 3.5 m

Question 6.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
Solution:
We have, d = 28cm
⇒ r = 14 cm
∵ Volume of a right circular cone = 9856 cm³

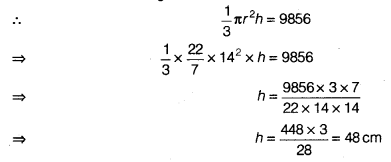
Question 7.
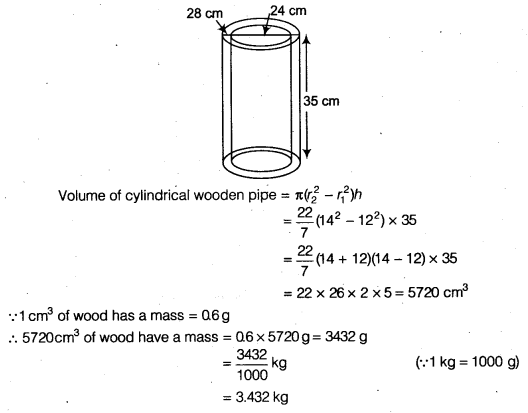
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
On revolving the right ∆ ABC about the side AB, we get a cone as shown in the adjoining figure.

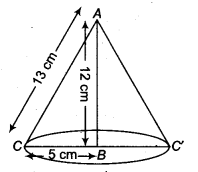
∴ Volume of the solid so obtained = \(\frac { 1 }{ 3 }\) πr²h
= \(\frac { 1 }{ 3 }\) x π x 5 x 5 x 4 = 100π cm³
Hence, the volume of the solid so obtained is 100π cm³.

Question 8.
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
On revolving the right ∆ ABC about the side BC( = 5 cm),
we get a cone as shown in the adjoining figure.

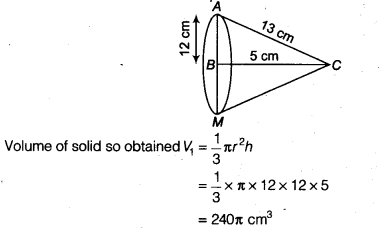
In above Question 7, the volume V₂ obtained by revolving the ∆ ABC about the side 12 cm i.e., V₂ = 100π cm³.

Hence, the required ratio =5:12

Question 9.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Solution:

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6

Question 1.
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000cm3 =1 L.)
Solution:
We have, circumference of the base = 132 cm
∴ 2πr = 132

Question 2.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm³ of wood has a mass of 0.6 g.
Solution:
Given, inner diameter = 24 cm
Inner radius (r₁) = 12cm
Outer diameter = 28 cm
Outer radius (r₂) = 14cm
h = 35cm

Question 3.
A soft drink is available in two packs
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm.
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Solution:
(i) We have, h = 15cm
l = 5cm, b = 4cm, h = 15 cm
Volume of cuboidical body =l x b x h= 5 x 4 x 15 = 300cm3 …(i)
(ii) We have, Diameter = 7cm
Radius, r = \(\frac { 7 }{ 2 }\) cm
Height, h = 10cm

∴ From Eqs. (i) and (ii), we see that volume of a plastic cylinder has greater capacity and its capacity is 385 – 300 = 85 cm3 is more than the tin can.

Question 4.
If the lateral surface of a cylinder is 94.2 cm² and its height is 5 cm, then find
(i) radius of its base,
(ii) its volume. (Use π = 3.14)
Solution:
We have, lateral surface of a cylinder = 94.2 cm² and h = 5 cm
∴ 2πrh = 94.2
⇒ 2 x 3.14 x r x 5 = 94.2
⇒ r = \(\frac { 94.2 }{ 31.4 }\)
⇒ r = 3 cm
(i) Hence, radius of base, r = 3cm
(ii) Volume of a cylinder = πr2h= 3.14(3)²x 5
= 3.14 x 9 x 5
= 141.3 cm³

Question 5.
It costs ₹2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of ₹20 per m², find
(i) inner curved surface area of the vessel,
(ii) radius of the base,
(iii) capacity of the vessel.
Solution:
We have, cost to paint the inner curved surface = ₹2200
Cost to paint per m² = ₹20

(i) Inner curved surface area of the vessel = 110m²
(ii) Hence, radius of the base is 1.75 m.
(iii) Capacity of the vessel = Volume of the vessel

Question 6.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Solution:
Capacity of a closed cylindrical vessel = 15.4 L
= 15.4 x 1000cm3 (∵ 1L = 1000 cm²)
∴ πr²h = 15400 cm³
πr² x 100 = 15400
r² = 154 x \(\frac { 7 }{ 22 }\) (∵ h= 1m= 100cm)
⇒ r² = 7 x 7
⇒ r = 7 cm
Total surface area of closed cylindrical vessel = 2πr(r + h)

Question 7.
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of. the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution:

Question 8.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution:
We have, diameter = 7cm
Radius, r = \(\frac { 7 }{ 22 }\) cm
h= 4 cm
Capacity of the cylindrical bowl = Volume of the cylinder = πr²h

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.6, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5

Question 1.
A matchbox measures 4 cm x 2.5 cm x 1.5 cm. What will be the volume of a packet containing 12 such boxes?
Solution:
Volume of a match box = 4 cm x 2.5 cm x 1.5 cm= 15 cm³
Volume of a packet = 12 x 15 cm³ = 180 cm³

Question 2.
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold? ( 1 m³ = 1000L)
Solution:
Volume of a cuboidal water tank = 6 m x 5 m x 4.5 m
= 30 x 4.5 m³ = 135 m³
= 135 x 1000L = 135000L (∵ 1 m³ = 1000L)

Question 3.
A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid?
Solution:
Volume of a cuboidal vessel = hold liquid
∴ l x b x h = 380 m3
⇒ 10 x 8 x h = 380
⇒ h = \(\frac { 380 }{ 80 }\)
⇒ h= 4.75m
Hence, the cuboidal vessel must be made 4.75 m high.

Question 4.
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of ₹30 per m3.
Solution:
Volume of a cuboidal pit = l x bx h= (8 x 6 x 3)m³ =144 m³
∵ Cost of digging per m³ = ₹ 30
∴ Cost of digging 144m³ = ₹ 30x 144 = ₹ 4320

Question 5.
The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are 2.5 m and 10 m, respectively.
Solution:
Given, l = 2.5 m and h = 10m
Let breadth of tank be b.

Hence, breadth of the cuboidal tank is 2 m.

Question 6.
A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20 m x 15 m x 6 m. For how many days will the water of this tank last?
Solution:

Question 7.
A go down measures 40 m x 25 m x 10 m. Find the maximum number of wooden crates each measuring 15 m x 125 m x 0.5 m that can be stored in the go down.
Solution:
Dimension for godown, l = 40m b = 25 m and c = 10 m
Volume of the godown = l x b x h= 40 m x 25 m x 10 m
Dimension for wooden gate l = 1.5 m, b = 1.25 m, b = 1.25 m, h = 0.5 m
Volume of wooden gates = l x b x h = 1.5 m x 1.25 m x 0.5m

Question 8.
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution:
Volume of a solid cube = 12 cm x 12 cm x 12 cm = 1728 cm³
The solid cube is cut into eight cubes of equal volume.

Question 9.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
Solution:
Given, l = 2 km= 2 x 1000 m = 2000m
b = 40 m
and h = 3 m
Since, the water flows at the rate of 2 km h^-1,
i.e., the water from 2 km of river flows into the sea in one hour.
The volume of water flowing into the sea in one hour = Volume of the cuboid
= l x b x h
= (2000 x 40 x 3) m³
= 240000 m³
∴ The volume of water flowing into the sea in one minute
= \(\frac { 240000 }{ 60 }\) m³
= 4000 m³

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4

Question 1.
Find the surface area of a sphere of radius
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
Solution:
(i) We have, r = 105 cm

Question 2.
Find the surface area of a sphere of diameter
(i) 14 cm
(ii) 21 cm
(iii) 3.5 m
Solution:

Question 3.
Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Solution:
We have, r = 10 cm
Total surface area of a hemisphere = 3πr²
= 3 x 3.14 x (10)²
= 9.42 x 100
= 942 cm²

Question 4.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution:
Let initial radius, r₁ = 7 cm
After increases, r₂ = 14 cm
Surface area for initial balloon = 4πr₁² = 4 x \(\frac { 22 }{ 7 }\) x 7 x 7 = 88 x 7
A₁ = 616 cm²
Surface area for increasing balloon = 4πr₂² = 4x \(\frac { 22 }{ 7 }\) x 14 x 14 = 88 x 28
A₂ = 2464 cm²
∴ Required ratio = A₁ : A₂ = 616 : 2464 = 1 : 4

Question 5.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹16 per 100 cm².
Solution:
We have, inner diameter = 10.5 cm
Inner radius = \(\frac { 10.5 }{ 2 }\) cm = 5.25 cm
Curved surface area of hemispherical bowl of inner side = 2πr²

Question 6.
Find the radius of a sphere whose surface area is 154 cm².
Solution:
Surface area of a sphere = 154 cm²

Hence, the radius of the sphere is 3.5 cm.

Question 7.
The diameter of the Moon is approximately one-fourth of the diameter of the Earth. Find the ratio of their surface areas.
Solution:
Let diameter of the Earth = d₁

Question 8.
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Solution:
Outer radius of the bowl = (Inner radius + Thickness)
= ( 5 + 0.25) cm = 5.25 cm

Question 9.
A right circular cylinder just encloses a sphere of radius r (see figure). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).
Solution:

The radius of the sphere = r
Radius of the cylinder = Radius of the sphere = r
Height of the cylinder = Diameter = 2r
(i) Surface area of the sphere A₁ = 4πr²
(ii) Curved surface area of the cylinder = 2πrh
A₂ = 2π x r x 2r
A₂ = 4πr²
(iii) Required ratio = A₁ :A₂ = 4πr² : 4πr² = 1 : 1

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3.

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3

Question 1.
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Solution:
We have, diameter = 10.5 cm
Radius (r) = \(\frac { 10.5 }{ 2 }\) = 5.25 cm
and slant height l= 10 cm
Curved surface area = πrl= \(\frac { 22 }{ 7 }\) x 5.25 x 10 = 165 cm²

Question 2.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution:
We have, slant height l = 21 m
and diameter = 24 cm

Question 3.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find
(i) radius of the base and
(ii) total surface area of the cone.
Solution:
We have, slant height, l= 14cm
Curved surface area of a cone = 308 cm²

Question 4.
A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹70.
Solution:
We have, h = 10 m

Hence, the slant height of the canvas tent is 26 m.
(ii) Canvas required to make the tent = Curved surface area of tent
= πrl
= π x 24 x 26 = 624π m²
∵ Cost of 1 m2 canvas = ₹ 70
Cost of 624n m2 canvas = ₹ 70 x 624π
= ₹ 70x 624 x \(\frac { 22 }{ 7 }\)
= ₹ 10 x 624 x 22
= ₹ 137280
Hence, the cost of the canvas is ₹ 137280.

Question 5.
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use π = 3.14)
Solution:
Let r, h and l be the radius, height and slant height of the tent, respectively.

The extra material required for stitching margins and cutting = 20 cm = Q² m Hence, the total length of tarpaulin required = 62.8 + Q² = 63 m

Question 6.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m².
Solution:
We have, slant height, l = 25m
and diameter = 14m
∴ Radius, r= 7m

Question 7.
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Solution:

∵ The sheet required to make 1 cap = 550 cm²
∴ The sheet required to make 10 caps = 550 x 10= 5500 cm²

Question 8.
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹12 per m², what will be the cost of painting all these cones? (Use π = 3.14 and take \( \sqrt{104} \) = 102)
Solution:

Curved surface area of a cone = πrl = 3.14 x 0.2 x 1.02 = 0.64056 m²
Cost of painting per m2 = ₹12
Cost of painting 0.64056 m2 = ₹12 x 0.64056= ₹ 7.68672
Cost of painting for 1 cone = ₹ 7.68672
Cost of painting 50 cones = ₹ 7.68672x 50= ₹ 384.336= ₹ 384.34

We hope the NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.3, drop a comment below and we will get back to you at the earliest.