Prasanna

RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Question 1.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm.
Solution:
Sides of triangle are 120 cm, 150 cm, 200 cm

Question 2.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm.
Solution:
Sides of a triangle are 9 cpi, 12 cm, 15 cm

Question 3.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Perimeter of a triangle = 42 cm
Two sides are 18 cm and 10 cm
Third side = 42 – (18 + 10)
= 42 – 28 = 14 cm

Question 4.
In a ∆ABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ∆ABC and hence its altitude on AC.
Solution:
Sides of triangle ABC are AB = 15 cm, BC = 13 cm, AC = 14 cm

Question 5.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 540 m
Ratio in sides = 25 : 17 : 12
Sum of ratios = 25 + 17 + 12 = 54

Question 6.
The perimeter of a triangle is 300 m. If its sides are in the ratio 3:5:7. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 300 m
Ratio in the sides = 3 : 5 : 7
∴ Sum of ratios = 3 + 5 + 7= 15

Question 7.
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution:
Perimeter of a triangular field = 240 dm
Two sides are 78 dm and 50 dm
∴ Third side = 240 – (78 + 50)
= 240 – 128 = 112 dm

Question 8.
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes.
Solution:
Sides of a triangle are 35 cm, 54 cm, 61 cm

Question 9.
The lengths of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Solution:
Ratio in the sides of a triangle = 3:4:5

Question 10.
The perimeter of an isosceles triangle is 42 cm and its base is (3/2) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Solution:
Perimeter of an isosceles triangle = 42 cm
Base = \(\frac { 3 }{ 2 }\) of its one of equal sides
Let each equal side = x, then 3
Base = \(\frac { 3 }{ 2 }\) x

Question 11.
Find the area of the shaded region in figure.

Solution:
In ∆ABC, AC = 52 cm, BC = 48 cm
and in right ∆ADC, ∠D = 90°
AD = 12 cm, BD = 16 cm
∴ AB²=AD² + BD² (Pythagoras Theorem)
(12)² + (16)² = 144 + 256 = 400 = (20)²
∴ AB = 20 cm

Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Construct a ∆ABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B = 60°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 4.8 cm.
(iii) Join EC.
(iv) Draw perpendicular bisector of CE which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 2.
Construct a ∆ABC in which AB + AC = 5.6 cm, BC = 4.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.5 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 5.6 cm and join CE.
(iii) Draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 3.
Construct a AABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.4 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 1.5 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of CE which intersects BE produced at A.
(v) Join AC.
∆ABC is the required triangle.

Question 4.
Using ruler and compasses only, construct a ∆ABC, given base BC = 7 cm, ∠ABC = 60° and AB + AC = 12 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 7 cm!
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 12 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of EC which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 5.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 10 cm.
(ii) At P, draw a ray PX making an angle of 90° and at Q, QY making an angle of 60°.
(iii) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of AP and AQ intersecting PQ at B and C respectively,
(v) Join AB and AC.
∆ABC is the required triangle.

Question 6.
Construct a triangle ABC such that BC = 6cm, AB = 6 cm and median AD = 4 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm and bisect it at D.
(ii) With centre B and radius 6 cm and with centre D and radius 4 cm, draw arcs intersecting each other at A.
(iii) Join AD and AB and AC.
Then ∆ABC is the required triangle.

Question 7.
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm

(ii) At B, draw a ray BX making an angle of 90° and cut off BE = 10 cm.
(iii) Join EC and draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 8.
Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 6.4 cm.
(ii) At P draw a ray PX making an angle of 60° and at Q, a ray QY making an angle of 45°.
(iii) Draw the bisector of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of PA and QA intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 9.
Using ruler and compasses only, construct a ∆ABC, from the following data:
AB + BC + CA = 12 cm, ∠B = 45° and ∠C = 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 12 cm.
(ii) Draw ray PX at P making are angle of 45° and at Q, QY making an angle of 60°.
(Hi) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(v) Draw the perpendicular bisector of AP and AQ intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 10.
Construct a triangle XYZ in which ∠Y = 30° , ∠Z = 90° XY +YZ + ZX = 11
Solution:
Steps of construction :
(i) Draw a line segment PQ =11 cm.
(ii) At P, draw a ray PL making an angle of 30° and Q, draw another ray QM making an angle of 90°.
(iii) Draw the angle bisector of ∠P and ∠Q intersecting each other at X.
(iv) Draw the perpendicular bisector of XP and XQ. Which intersect PQ at Y and Z respectively.
(v) Join XY and XZ.
Then ∆XYZ is the required triangle

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Solution:
Steps of construction :
(i) Draw an angle BAC.
(ii) Draw a line DF.
(iii) With centre A and D, draw arcs of equal radius which intersect AC at L and AB at M and DF at P.
(iv) Cut off PQ = LM and join DQ and produce it to E, then
∠EDF = ∠BAC.

Question 2.
Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Solution:
Steps of construction :
(i) Draw an angle ABC which is an obtuse i.e. more than 90°.
(ii) With centre B and a suitable radius draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
ThenBD is die bisector of ∠ABC.
On measuring each part, we find each angle = 53°.

Question 3.
Using your protractor, draw an angle of measure 108°. With this angle as given, draw an angle of 54°.
Solution:
Steps of construction :
(i) With the help of protractor draw an angle ABC = 108°.
As 54° = \(\frac { 1 }{ 2 }\) x 108°
∴ We shall bisect it.

(ii) With centre B and a suitable radius, draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF, draw arcs intersecting each other at G
(iv) Join BG and produce it to D.
Then ∠DBC = 54°.

Question 4.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Solution:
Steps of construction :
(i) Using protractor, draw a right angle ∆ABC.
i. e. ∠ABC = 90°.
(ii) With centre B and a suitable radius, draw an arc which meets BC at E and BA at F.
(iii) With centre E and F, draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC =\(\frac { 1 }{ 2 }\) x 90° = 45°.

Question 5.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution:
Steps of construction :
(i) Draw a linear pair ∠DCA and ∠DCB.
(ii) Draw the bisectors of ∠DCA and ∠DCB. Forming ∠ECF on measuring we get ∠ECF = 90°.
Verification : ∵∠DCA + ∠DCB = 180°
⇒ \(\frac { 1 }{ 2 }\) ∠DCA + \(\frac { 1 }{ 2 }\) ∠DCB = 180° x \(\frac { 1 }{ 2 }\) = 90°
∴ ∠ECF = 90°
i.e. EC and FC are perpendicular to each other.

Question 6.
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line
Solution:
Steps of construction :
(i) Draw two lines AB and CD intersecting each other at O.
(ii) Draw the bisector of ∠AOD and also the bisector of ∠BOC. Which are OP and OQ respectively. We see that OP and OQ are in the same straight line.

Question 7.
Using ruler and compasses only, draw a right angle.
Solution:
Steps of construction :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius, draw an arc meeting BC at E.
(iii) With centre E and same radius, cut off arcs EF and FG.
(iv) Bisect arc FG at H.
(v) Join BH and produce it to A.
Then ∠ABC = 90°.

Question 8.
Using ruler and compasses only, draw an angle of measure 135°.
Solution:
Steps of construction :
(i) Draw a line DC and take a point B on it.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P, cut off arcs PQ, QR and RS.
(iv) Bisect as QR at T and join BT and produce it to E.
(v) Now bisect the arc KS at RL.
(vi) Join BL and produce it to A.
Now ∠ABC = 135°.

Question 9.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Solution:
Steps of construction :
(i) Draw an angle ABC = 12° with the help of protractor.
(ii) With centre B and a suitable radius, draw an arc EF.
(iii) With centre E and F, draw arcs intersecting
each other at G and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC = 72° x \(\frac { 1 }{ 2 }\) = 36°.
(iv) Again bisect ∠ABD in the same way then PB is the bisector of ∠ABD.
∴ ∠PBC = 36° + \(\frac { 1 }{ 2 }\) x 36°
= 36° + 18° = 54°
Hence ∠PBC = 54°

Question 10.
Construct the following angles at the initial point of a given ray and justify the construction:
(i) 45°
(ii) 90°
Solution:
(i) 45°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) With centre E, cut off equal arcs EF and FG.
(d) Bisect FG at H.
(e) Join BH and produce to X so that ∠XBC = 90°.
(f) Bisect ∠XBC so that ∠ABC = 45°.

(ii) 90°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E and with centre E cut off arcs from E, EF = FG
(c) Now bisect the arc EG at H.
(d) Join BH and produce it to A.
∴ ∠ABC = 90°.

Question 11.
Construct the angles of the following measurements:
(i) 30°
(ii) 75°
(iii) 105°
(iv) 135°
(v) 15°
(vi) 22 \(\frac { 1 }{ 2 }\)°
Solution:
(i) 30°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) Cut off arcs EF and bisect it at G.
So that ∠ABC = 30°.

(ii) 75°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF = FG from E.
(d) Bisect the arc FG at K and join BK so that ∠KBC = 90°.
(e) Now bisect arc HF at L and join BL and produce it to A so that ∠ABC = 75°.

(iii) 105°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) From E, cut off arc EF = FG and divide FG at H.
(d) Join BH meeting the arc at K.
(e) Now bisect the arc KG at L.
Join BL and produce it to A.
Then ∠ABC = 105°.

(iv) 135°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) From E, cut off EF = FG = GH.
(d) Bisect arc FG at K, and join them.
(e) Bisect arc KH at L.
(f) Join BL and produce it to A, then ∠ABC = 135°.

(v) 15°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF from E and bisect it at G. Then ∠GBC = 30°.
(d) Again bisect the arc EJ at H.
(e) Join BH and produce it to A.
Then ∠ABC = 15°.

(vi) 22 \(\frac { 1 }{ 2 }\)°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc and from E, cut off EF = FG
(c) Bisect FG at H so that ∠HBC = 90°.
(d) Now bisect ∠HBC at K. So that ∠YBC = 45°.
(e) Again bisect ∠YBC at J. So thttt ∠ABC = 22 \(\frac { 1 }{ 2 }\)°

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Draw a line segment of length 8.6 cm. Bisect it and measure the length of each part.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8.6 cm.
(ii) With centres A and B, and radius more than half of AB, draw arcs which intersect each other at E and F, on both sides of AB.
(iii) Join EF which intersects AB at D.
D is the required mid point of AB.
Measuring each part, it is 4.3 cm long.

Question 2.
Draw a line segment AB of length 5.8 cm. Draw the perpendicular bisector of this line segment.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5.8 cm.
(ii) With centres A and B and radius more than half of AB, draw arcs intersecting each other at E and F.
(iii) Join EF which is the required perpendicular bisector of AB.

Question 3.
Draw a circle with centre at point O and radius 5 cm. Draw its chord AB, draw the perpendicular bisector of line segment AB. Does it pass through the centre of the circle?
Solution:
Steps of construction :
(i) Draw a circle with centre O and radius 5 cm.
(ii) Draw a chord AB of the circle.
(iii) With centres A and B and radius more than half of AB draw arcs intersecting each other at P and Q.
(iv) Join PQ which intersects AB at D and passes through O, the centre of the circle.

Question 4.
Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not parallel to CD. Draw the perpendicular bisectors of AB and CD. At what point do they intersect?
Solution:
Steps of construction :
(i) Draw a circle with centre O and a suitable radius.
(ii) Draw two chords AB and CD which are not parallel to each other.
(iii) Draw the perpendicular bisectors of AB and CD with the help of ruler and compasses. We see that these two chords intersect each other at the centre O, of the circle.

Question 5.
Draw a line segment of length 10 cm and bisect it. Further bisect one of the equal parts and measure its length.
Solution:
Steps of construction :
(i) Draw a line segment AB = 10 cm.
(ii) With the help of ruler and compasses, bisect AB at C.
(iii) Bisect again AC at D.
Measuring AD, it is 2.5 cm long.

Question 6.
Draw a line segment AB and bisect it. Bisect one of the equal parts to obtain a line segment of length \(\frac { 1 }{ 2 }\) (AB).
Solution:
Steps of construction :
(i) Draw a line segment AB.
(ii) With the help of ruler and compasses, draw the bisector of AB which bisects AB at C.
(iii) Similarly, in the same way draw the bisector of AC at D.
We see that AC = \(\frac { 1 }{ 2 }\) (AB).

Question 7.
Draw a line segment AB and by ruler and compasses, obtain a line segment of length \(\frac { 3 }{ 4 }\) (AB).
Solution:
Steps of construction :
(i) Draw a line segment AB.
(ii) Draw a ray AX making an acute angle with A3 and equal 4 parts at A₁, A₂, A₃ and A₄.
(iii) JoinA₄B.
(iv) From A3, draw a line parallel to A₄B which meets AB at C.
C is the required point and AC = \(\frac { 3 }{ 4 }\) (AB).

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

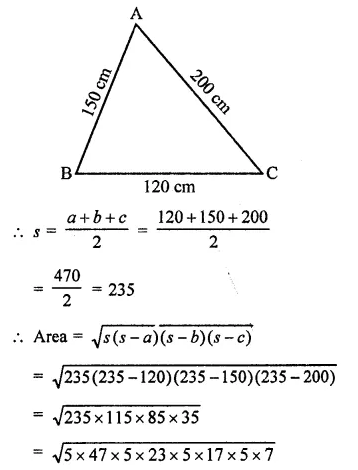
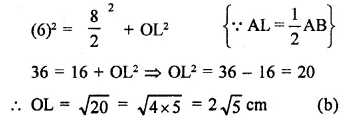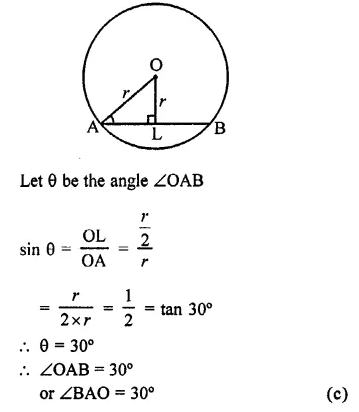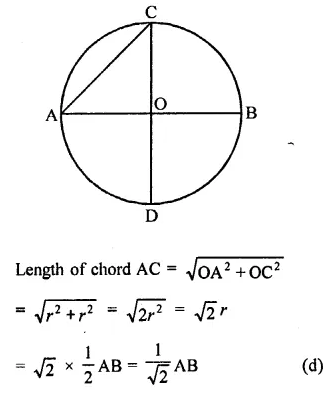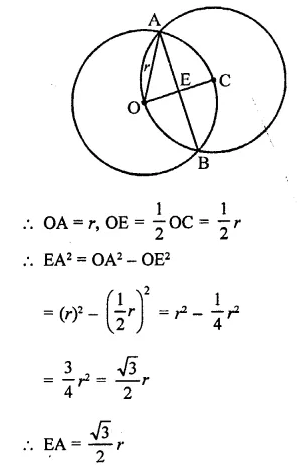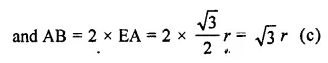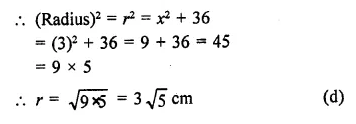RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Mark the correct alternative in each of the following:
Question 1.
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
(a) 15 cm
(b) 16 cm
(c) 17 cm
(d) 34 cm
Solution:
Length of chord AB of circle = 16 cm
Distance from the centre OL = 15 cm

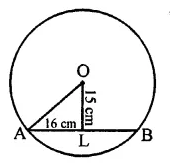
Let OA be the radius, then in right ∆OAL,
OA² = OL² + AL²
16
= (15)² + \(\frac { 16 }{ 2 }\) = 15² + 8²
= 225 + 64 = 289 = (17)²
∴ OA = 17 cm
Hence radius of the circle = 17 cm (c)

Question 2.
The radius of a circle Js 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is

Solution:
Radius of the cirlce (r) = 6 cm
Perpendicular distance from centre = ?
Length of chord = 8 cm

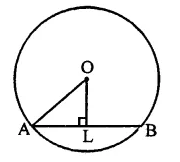
Let AB be chord, OL is the distance
In right ∆OAL
OA² = AL² + OL²

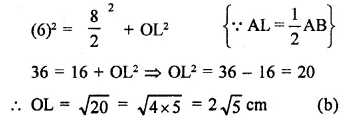
Question 3.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance \(\frac { r }{ 2 }\) from O, then ∠BAO =
(a) 60°
(b) 45°
(c) 30°
(d) 15°
Solution:
r is the radius of the circle with centre O
AB is the chord, at a distance of \(\frac { r }{ 2 }\) from the centre

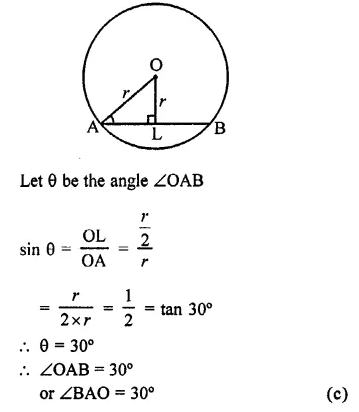
Question 4.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB=
(a) 70°
(b) 100°
(c) 125°
(d) 150°
Solution:
ABCD is a cyclic quadrilateral ∠DCA = 80° and ∠ADB = 30°

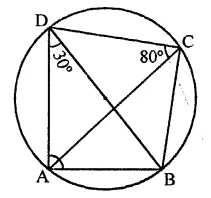
∵∠ADB = ∠ACB (Angles in the same segment)
∴ ∠ACB = 30°
∴ ∠BCD = 80° + 30° = 110°
∵ ABCD is a cyclic quadrilateral
∴∠BAD + ∠BCD = 180°
⇒ ∠BAD + 110°= 180°
⇒ ∠BAD = 180°- 110° = 70°
or ∠DAB = 70° (a)

Question 5.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
(a) 12 cm
(b) 14 cm
(c) 16 cm
(d) 18 cm
Solution:
In a circle AB chord = 14 cm
and distance from centre OL = 6 cm
Let r be the radius of the circle, then OA² = AL² + OL²
⇒ r² = (7)² + (6)² = 49 + 36 = 85

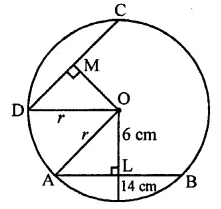
In the same circle length of another chord CD = ?
Distance from centre = 2 cm
∴ r² = OM² + MD²
⇒ 85 = (2)² + DM²
⇒ 85 = 4 + DM²
⇒ DM² = 85-4 = 81 = (9)²
∴ DM = 9
∴ CD = 2 x DM = 2 x 9 = 18 cm
∴Length of another chord = 18 cm (d)

Question 6.
One chord of a circle is known to be 10 cm. The radius of this circle must be
(a) 5 cm
(b) greater than 5 cm
(c) greater than or equal to 5 cm
(d) less than 5 cm
Solution:
Length of chord of a circle = 10 cm
Length of radius of the circle greater than half of the chord
More than \(\frac { 10 }{ 2 }\) = 5 cm (b)

Question 7.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with O as centre and OC as radius. The length of the chord of this circle passing through C and B is
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 6 cm
Solution:
In right ∆ABC, ∠B = 90°
AC = 5 cm, AB = 4 cm

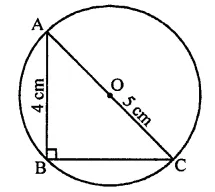
∴ BC² = AC² -AB²
= 5² – 4² = 25 – 16
= 9 = (3)²
∴ BC = 3 cm
∴ Length of chord BC = 3 cm (a)

Question 8.
If AB, BC and CD are equal chords of a circle with O as centre, and AD diameter then ∠AOB =
(a) 60°
(b) 90°
(c) 120°
(d) none of these
Solution:
In a circle chords AB = BC = CD

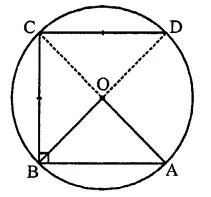
O is the centre of the circle
∴ ∠AOB = cannot be found (d)

Question 9.
Let C be the mid-point of an arc AB of a circle such that m \(\breve { AB }\) = 183°. If the region bounded by the arc ACB and line segment AB is denoted by S, then the centre O of the circle lies
(a) in the interior of S
(b) in the exterior of S
(c) on the segment AB
(d) on AB and bisects AB
Solution:
\(\breve { AB }\) = 183°
∴ AB is the diameter of the circle with centre O and C is the mid point of arc AB

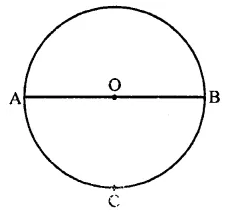
Line segment AB = S
∴ Centre will lie on AB (c)

Question 10.
In a circle, the major arc is 3 ti.nes the minor arc. The corresponding central angles and the degree measures of two arcs are
(a) 90° and 270°
(b) 90° and 90°
(c) 270° adn 90°
(d) 60° and 210°
Solution:
In a circle, major arc is 3 times the minor arc i.e. arc ACB = 3 arc ADB
∴ Reflex ∠AOB = 3∠AOB
But angle at O = 360°

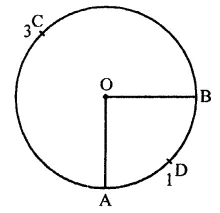
and let ∠AOB = x
Then reflex ∠ADB = x
x + 3x – 360°
⇒ 4x = 360°
⇒ x = \(\frac { { 62 }^{ \circ } }{ 2 }\)  = 90°
∴ 3x = 90° x 3 = 270°
Here angles are 270° and 90° (c)

Question 11.
If A and B are two points on a circle such that m(\(\breve { AB }\)) = 260°. A possible value for the angle subtended by arc BA at a point on the circle is
(a) 100°
(b) 75°
(c) 50°
(d) 25°
Solution:
A and B are two points on the circle such that reflex ∠AOB = 260°

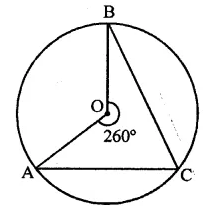
∴ ∠AOB = 360° – 260° = 100°
C is a point on the circle
∴ By joining AC and BC,
∠ACB = \(\frac { 1 }{ 2 }\)∠AOB = \(\frac { 1 }{ 2 }\) x 100° = 50° (c)

Question 12.
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOC is
(a) 30°
(b) 60°
(c) 90°
(d) 120°
Solution:
∆ABC is an equilateral triangle inscribed in a circle with centre O

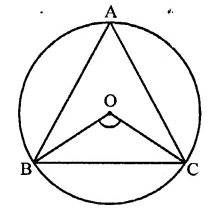
∴ Measure of ∠BOC = 2∠BAC
= 2 x 60° = 120° (d)

Question 13.
If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
(a) rhombus
(b) rectangle
(c) parallelogram
(d) square
Solution:
Two diameter of a circle AB and CD intersect each other at right angles

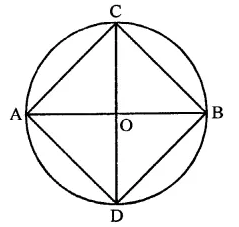
AD, DB, BC and CA are joined forming a quad. ABCD.
∵ The diagonals are equal and bisect each other at right angles
∴ ACBD is a square (d)

Question 14.
In ABC is an arc of a circle and ∠ABC = 135°, then the ratio of arc \(\breve { AB }\) to the circumference is
(a) 1 : 4
(b) 3 : 4
(c) 3 : 8
(d) 1 : 2
Solution:
Arc ABC of a circle and ∠ABC = 135°
Join OA and OC

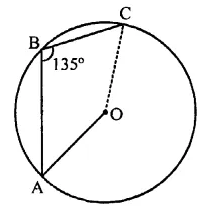
∴ Angle subtended by arc ABC at the centre = 2 x ∠ABC = 2 x 135° = 270°
Angle at the centre of the circle = 360°
∴ Ratio with circumference = 270° : 360° = 3:4 (b)

Question 15.
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
(a) 60°
(b) 75°
(c) 120°
(d) 150°
Solution:
The chord of a circle = radius of the circle In the figure OA = OB = AB

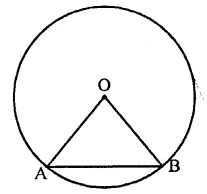
∴ ∠AOB = 60°
(Each angle of an equilateral = 60°) (a)

Question 16.
PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
(a) 41°
(b) 23°
(c) 67°
(d) 18°
Solution:
PQRS is a cyclic quadrilateral with centre O and ∠QPR = 67°
∠SPR = 72°

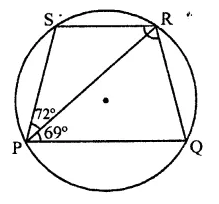
∴ ∠QPS = 67° + 72° = 139°
∵ ∠QPS + ∠QRS = 180° (Sum of opposite angles of a cyclic quad.)
⇒ 139° + ∠QRS = 180°
⇒ ∠QRS = 180° – 139° = 41° (a)

Question 17.
If A, B, C are three points on a circle with centre O such that ∠AOB = 90° and ∠BOC = 120°, then ∠ABC =
(a) 60°
(b) 75°
(c) 90°
(d) 135°
Solution:
A, B and C are three points on a circle with centre O
∠AOB = 90° and ∠BOC = 120°

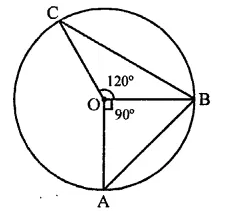
∴ ∠AOC = 360° – (120° + 90°)
= 360° -210°= 150°
But ∠AOC is at the centre made by arc AC and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\) ∠AOC
= \(\frac { 1 }{ 2 }\) x 150° = 75° (b)

Question 18.
The greatest chord of a circle is called its
(a) radius
(b) secant
(c) diameter
(d) none of these
Solution:
The greatest chord of a circle is called its diameter. (c)

Question 19.
Angle formed in minor segment of a circle is
(a) acute
(b) obtuse
(c) right angle
(d) none of these
Solution:
The angle formed in minor segment of a circle is obtuse angle. (b)

Question 20.
Number of circles that can be drawn through three non-collinear points is
(a) 1
(b) 0
(c) 2
(d) 3
Solution:
The number of circles that can pass through three non-collinear points is only one. (a)

Question 21.
In the figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
(a) 45°
(b) 60°
(c) 75°
(d) 90°

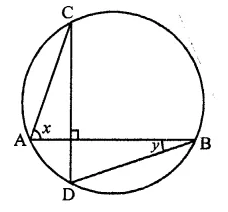
Solution:
In the circle, AB and CD are two chords which intersect each other at P at right angle i.e. ∠CPB = 90°

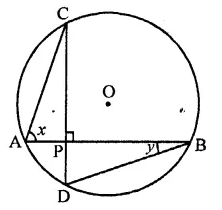
∠CAB and ∠CDB are in the same segment
∴ ∠CDB = ∠CAB = x
Now in ∆PDB,
Ext. ∠CPB = ∠D + ∠DBP
⇒ 90° = x + y (∵ CD ⊥ AB)
Hence x + y = 90° (d)

Question 22.
In the figure, if ∠ABC = 45°, then ∠AOC=
(a) 45°
(b) 60°
(c) 75°
(d) 90°

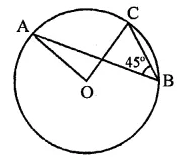
Solution:
∵ arc AC subtends
∠AOC at the centre of the circle and ∠ABC
at the remaining part of the circle

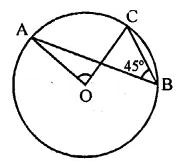
∴ ∠AOC = 2∠ABC
= 2 x 45° = 90°
Hence ∠AOC = 90° (d)

Question 23.
In the figure, chords AD and BC intersect each other at right angles at a point P. If ∠D AB = 35°, then ∠ADC =
(a) 35°
(b) 45°
(c) 55°
(d) 65°

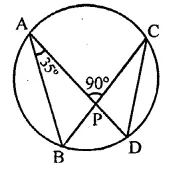
Solution:
Two chords AD and BC intersect each other at right angles at P, ∠DAB = 35°
AB and CD are joined
In ∆ABP,
Ext. ∠APC = ∠B + ∠A

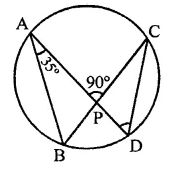
⇒ 90° = ∠B + 35°
∠B = 90° – 35° = 55°
∵ ∠ABC and ∠ADC are in the same segment
∴ ∠ADC = ∠ABC = 55° (c)

Question 24.
In the figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
(a) 42°
(b) 48°
(c) 58°
(d) 52°

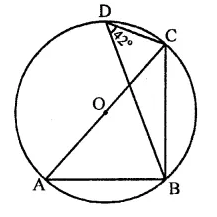
Solution:
In the figure, O is the centre of the circle
∠BDC = 42°
∠ABC = 90° (Angle in a semicircle)
and ∠BAC and ∠BDC are in the same segment of the circle.
∴ ∠BAC = ∠BDC = 42°
Now in ∆ABC,
∠A + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)

⇒ 42° + 90° + ∠ACB = 180°
⇒ 132° + ∠ACB – 180°
⇒ ∠ACB = 180° – 132° = 48° (b)

Question 25.
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is

Solution:
AB and CD are two diameters of a circle with centre O

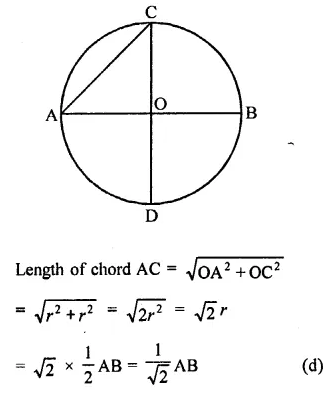
Question 26.
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circles is

Solution:
Two equal circles pass through the centre of the other and intersect each other at A and B
Let r be the radius of each circle

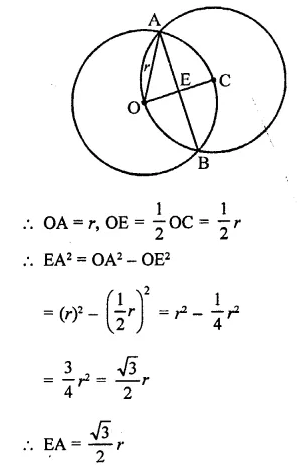
Question 27.
If AB is a chord of a circle, P and Q are the two points on the circle different from A and B,then
(a) ∠APB = ∠AQB
(b) ∠APB + ∠AQB = 180° or ∠APB = ∠AQB
(c) ∠APB + ∠AQB = 90°
(d) ∠APB + ∠AQB = 180°
Solution:
AB is chord of a circle,
P and Q are two points other than from points A and B

∵ ∠APB and ∠AQB are in the same segment of the circle
∴ ∠APB = ∠AQB (a)

Question 28.
AB and CD are two parallel chords of a circle with centre O such that AB = 6 cm and CD = 12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is

Solution:
AB and CD are two parallel chords of a circle with centre O
Let r be the radius of the circle AB = 6 cm, CD = 12 cm
and distance between them = 3 cm
Join OC and OA, LM = 3 cm

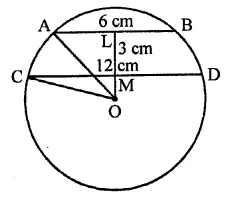
Let OM = x, then OL = x + 3

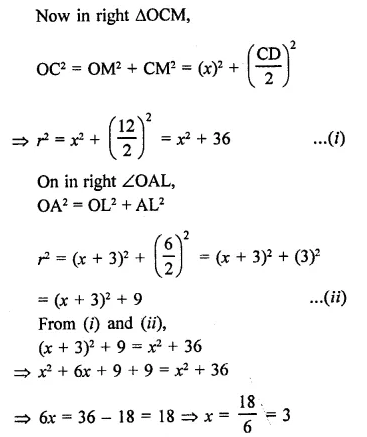
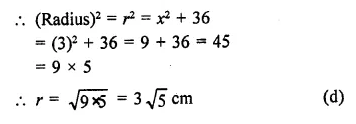
Question 29.
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. This distance between the chords is 23 cm. If the length of one chord is 16 cm then the length of the other is
(a) 34 cm
(b) 15 cm
(c) 23 cm
(d) 30 cm
Solution:
Radius of a circle = 17 cm
The distance between two parallel chords = 23 cm
AB || CD and LM = 23 cm
Join OA and OC,
∴ OA = OC = 17 cm
Let OL = x, then OM = (23 – x) cm
AB = 16 cm
Now in right ∆OAL,
OA² = OL2² + AL²
⇒ (17)² = x² + AL²
⇒ 289 = x² + AL²

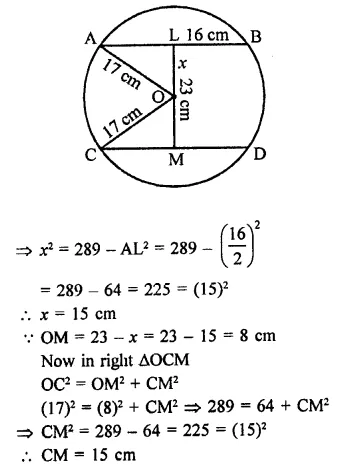
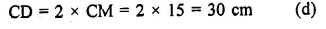
Question 30.
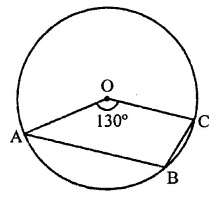
In the figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =
(a) 130°
(b) 115°
(c) 65°
(d) 165°

Solution:
O is the centre of the circle and ∠AOC = 130°
Reflex ∠AOC = 360° – 130° = 230°

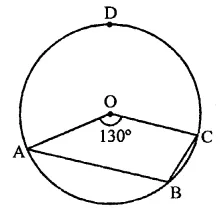
Now arc ADB subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\)reflex ∠AOC
= \(\frac { 1 }{ 2 }\) x 230°= 115° (b)

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.