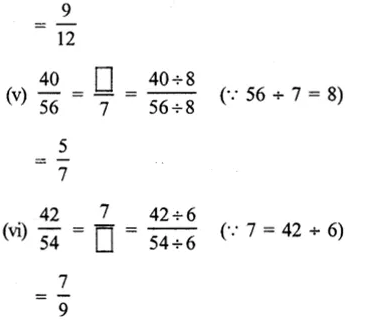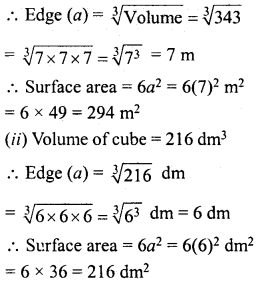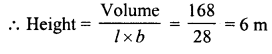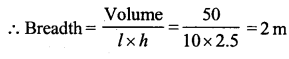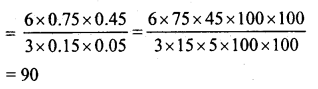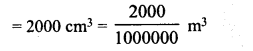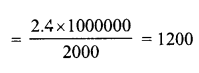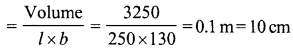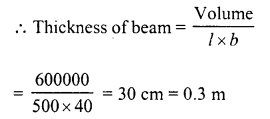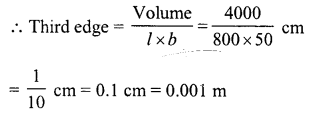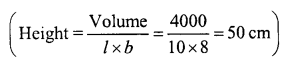Prasanna

RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4

Question 1.
Find the surface area of a cuboid whose :
(i) length = 10 cm, breadth = 12 cm and height = 14 cm
(ii) length = 6 dm, breadth = 8 dm, height = 10 dm
(iii) length = 2 m, breadth = 4 m and height = 5 m
(iv) length = 3.2 m, breadth = 30 dm, height = 250 cm.
Solution:
(i) Length of cuboid (l) = 10 cm
Breadth (b) = 12 cm
Height (h) = 14 cm
∴ Surface area = 2(1 × b + b × h + h × l)
= 2(10 x 12 + 12 x 14 + 14 x 10) cm²
= 2(120+ 168 + 140) cm²
= 2 x 428 = 856 cm²
(ii) Length of cuboid (l) = 6 dm
Breadth (b) = 8 dm
Height (h) = 10 dm
∴ Surface area = 2 ( l × b + b x h + h× l)
= 2(6 x 8 + 8 x 10 + 10 x 6) dm²
= 2(48 + 80 + 60) dm² = 2 x 188 = 376 dm²
(iii) Length of cuboid (l) = 2 m
Breadth (b) = 4 m
Height (h) = 5 m
∴ Surface area = 2(l × b + b × h + h × l)
= 2(2 x 4 + 4 x 5 + 5 x 2) m2
= 2(8 + 20 + 10) m2 = 76 m2
(iv) Length of cuboid (l) = 3.2 m = 32 dm
Breadth (b) = 30 dm
Height (h) = 250 cm = 25 dm
∴ Surface area = 2(1 x b + b x h + h x l)
= 2(32 x 30 + 30 x 25 + 25 x 32) dm²
= 2(960 + 750 + 800) dm²
= 2 x 2510 = 5020 dm²

Question 2.
Find the surface area of a cube whose edge is
(i) 1.2 m
(ii) 27 cm
(iii) 3 cm
(iv) 6 m
(v) 2.1m
Solution:
(i) Edge of the cube (a) = 1.2 m
∴ Surface area = 6a²= 6 x (1,2)² m²
= 6 x 1.44 = 8.64 m²
(ii) Edge of cube (a) = 27 cm
∴ Surface area = 6a² = 6 x (27)² m²
= 6 x 729 = 4374 m²
(iii) Edge of cube (a) = 3 cm
Surface area = 6a² = 6 x (3)² m²
= 6×9 cm² = 54 cm²
(iv) Edge of cube (a) = 6 m
∴ Surface area = 6a² = 6 x (6)2 m²
= 6 x 6 x 6 = 216 m²
(v) Edge of the cube (a) = 2.1 m
∴ Surface area = 6a2 = 6 x (2.1)2 m²
= 6 x 4.41 = 26.46 m²

Question 3.
A cuboidal box is 5 cm by 5 cm by 4 cm. Find its surface area.
Solution:
Length of cuboid box (l) = 5 cm
Breadth (b) = 5 cm
and height (h) = 4 cm
∴ Surface area = 2 (l x b + b x h + h x l)
= 2 (5 x 5 + 5 x 4 + 4 x 5) cm²
= 2 (25 + 20 + 20)
= 2 x 65 cm²
= 130 cm²

Question 4.
Find the surface area of a cube whose volume is :
(i) 343 m³
(ii) 216 dm³.
Solution:
(i) Volume of a cube = 343 m³

Question 5.
Find the volume of a cube whose surface area is
(i) 96 cm²
(ii) 150 m².
Solution:
(i) Surface area of a cube = 96 cm²

Question 6.
The dimensions of a cuboid are in the ratio 5:3:1 and its total surface area is 414 m². Find the dimensions.
Solution:
Ratio in .dimensions = 5 : 3 : 1
Let length (l) = 5x
breadth (b) = 3x
and height (h) = x
∴ Surface area = 2(1 x b + b x h + h x l)
= 2(5x x 3x + 3x x x + x x 5x)
= 2(15×2 + 3×2 + 5×2) = 2 x 23×2 = 46×2

Question 7.
Find the area of the cardboard required to make a closed box of length 25 cm, 0.5 m and height 15 cm.
Solution:
Length of cardboard (l) = 25 cm
Breadth (b) = 0.5 m = 50 cm
Height (h)= 15 cm.
∴ Surface area of cardboard = 2 (l x b + b x h + h x l)
= 2(25 x 50 + 50 x 15 + 15 x 25) cm²
= 2(1250+ 750+ 375) cm²
= 2(2375)
= 4750 cm²

Question 8.
Find the surface area of a wooden box whose shape is of a cube and if the edge of the box is 12 cm.
Solution:
Edge of cubic wooden box = 12 cm
∴ Surface area = 6a² = 6(12)² cm²
= 6 x 144 = 864 cm²

Question 9.
The dimensions of an oil tin are 26 cm x 26 cm x 45 cm. Find the area of the tin sheet required for making 20 such tins. If 1 square metre of the tin sheet costs Rs 10, find the cost of the tin sheet used for these 20 tins.
Solution:
Length of tin (l) = 26 cm = 0.26 m
Breadth (b) = 26 cm = 0.26 m
Height (h) = 45 cm = 0.45 m
∴ Surface area = 2(l x b + b x h +h xl)
= 2(0.26 x 0.26 + 0.26 x 0.45 + 0.45 x 0.26) m²
= 2(0.0676 + 0.117 + 0.117) m²
= 2(0.3016) = 0.6032 m²
Sheet required for such 20 tins
= 0.6032 x 20= 12.064 m²
Cost of 1 m² tin sheet = 10 m
∴ Total cost = Rs 12.064 x 10 = Rs 120.64
and area of sheet = 12.064 m² = 120640 cm²

Question 10.
A classroom is 11 m long, 8 m wide and 5 m high. Find the sum of the areas of its floor and the four walls (including doors, windows etc.)
Solution:
Length of room (l) = 11 m
Width (b) = 8 m
and height (h) = 5 m
Area of floor = l x b = 11 x8 = 88m2
Area of four walls = 2 (l + b) x h
= 2(11 + 8) x 5 m² = 2 x 19×5 = 190 m²
∴ Total area = 88 m² + 190 m² = 278 m²

Question 11.
A swimming pool is 20 m long, 15 m wide and 3 m deep. Find the cost of repairing the floor and wall at the rate of Rs 25 per square metre.
Solution:
Length of pool (l) = 20 m
Breadth (b) = 15 m
and Depth (h) = 3 m.
Area of floor = l x b = 20 x 15 = 300 m²
and area of its walls = 2(l + b) x h
= 2(20 + 15) x 3 = 2 x 35 x 3 m² = 210 m²
∴ Total area = 300 + 210 = 510 m²
Rate of repairing it = Rs 25 per sq. metre
∴ Total cost = Rs 25 x 510 = Rs 12750

Question 12.
The perimeter of a floor of a room is 30 m and its height is 3 m. Find the area of four walls of the room.
Solution:
Perimeter of floor = 30 m
i.e. 2(1 + b) = 30 m
Height = 3 m
∴ Area of four walls = Perimeter x height = 30 x 3 = 90 m²

Question 13.
Show that the product of the areas of the floor and two adjacent walls of a cuboid is the square of its volume.
Solution:
Let length of the room = l
and breadth = b
and height = h
Volume = l x b x h
Area of floor = l x b = lb.
Area of two adjacent walls = hl x bh.
∴ Product of areas of floor and two adjacent walls of the room = lb (hi x bh)
= l²b²h² = (l.b.h)² = (Volume)²
Hence proved

Question 14.
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5, 3m and 350 cm, respectively. Find the cost of plastering at the rate of Rs 8 per square metre.
Solution:
Length of room (l) = 4.5 m
Width (b) = 3 m
and height (h) = 350 cm = 3.5 m
∴ Area of walls = 2(l + b) x h
= 2(4.5 + 3) x 3.5 m² = 2 x 7.5 x 3.5 m² = 52.5 m²
Area of ceiling = l x b = 4.5 x 3 = 13.5 m²
∴ Total area = 52.5 + 13.5 m² = 66 m²
Rate of plastering = Rs 8 per sq. m
∴ Total cost = Rs 8 x 66 = Rs 528

Question 15.
A cuboid has total surface area of 50 m² and lateral surface area its 30 m². Find the area of its base.
Solution:
Total surface area of cuboid = 50 m²
Lateral surface area = 30 m²
∴ Area of floor and ceiling = 50 – 30 = 20 m²
But area of floor = area of ceiling
∴ Area of base (floor) = \(\frac { 20 }{ 2 }\) = 10 m²

Question 16.
A classroom is 7 m long, 6 m broad and 3.5 m high. Doors and windows occupy an area of 17 m². What is the cost of white-washing the walls at the rate of Rs 1.50 per m².
Solution:
Length of room (l) = 7 m
Breadth (b) = 6 m
and height (h) = 3.5 m
∴ Area of four walls = 2(1 + b) x h
= 2(7 + 6) x 3.5 m² = 2 x 13 x 3.5 = 91 m²
Area of doors and windows = 17 m2
∴ Remaining area of walls = 91 – 17 = 74 m²
Rate of whitewashing = Rs 1.50 per m²
∴ Total cost = 74 x Rs 1.50 = Rs 111

Question 17.
The central hall of a school is 80 m long and 8 m high. It has 10 doors each of size 3 m x 1.5 m and 10 windows each of size 1.5 m x l m. If the cost of the white-washing the walls of the hall at the rate of Rs 1.20 per m² is Rs 2385.60, find the breadth of the hall.
Solution:
Length of hall (l) = 80 m
Height (h) = 8 m
Size of each door = 3 m x 1.5 m
∴ Area of 10 doors = 3 x 1,5 x 10 m²
= 45 m²
A size of each windows = 1.5 m x 1 m
∴ Area of 10 windows = 1.5 m x 1 x 10= 15 m²
Total cost of whitewashing the walls = Rs 2385.60
Rate of whitewashing = Rs 1.20 per m²
∴ Area of walls which are whitewashed

Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
• RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4

Question 1.
Find the volume in cubic metres (cu.m) of each of the cuboids whose dimensions are :
(i) length = 12 cm, breadth = 10 m, height = 4.5 m
(ii) length = 4 m, breadth = 2.5 m, height = 50 cm
(iii) length = 10 m, breadth = 25 dm, height = 25 cm.
Solution:
(i) Length of cuboid (l) = 12 m
Breadth (b) = 10m
and height (h) = 4.5 m
∴Volume = l x b x h = 12 x 10 x 4.5 m³
= 540 m³
(ii) Length of cuboid (l) = 4 m
Breadth (b) = 2.5m
Height (h) = 50 cm = 0.5 m
∴ Volume = l x b x h = 4 x 2.5 x 0.5 = 5 m³
(iii) Length of cuboid (l) = 10 m
Breadth (b) = 25 dm = 2.5 m
Height (h) = 25 cm 0.25 m
∴ Volume = l x b x h = 10 x 2.5 x 0.25 m³ = 6.25 m³

Question 2.
Find the volume in cubic decimetre of each of the cubes whose side is
(i) 1.5 m
(it) 75 cm
(iii) 2 dm 5 cm
Solution:
(i) Side of cube (a) = 1.5 m
∴ Volume = a³ = (1.5)³ m³
= 1.5 x 1.5 x 1.5 m³ = 3.375 m³
= 3.375 x 1000 = 3375 dm³
(ii) Side of cube (a) = 75 cm = 7.5 dm
∴ Volume = a³ = (7.5)3 dm³
= 421.875 dm³
(iii) Side of cube (a) = 2 dm 5 cm = 2.5 dm
∴ Volume = (a)³ = (2.5)³ dm³
= 15.625 dm³

Question 3.
How much clay is dug out in digging a well measuring 3m by 2m by 5m?
Solution:
Length of well (l) = 3m
breadth (b) = 2 m
and height (depth) (h) = 5 m
Volume of earth dug out = l x b x h = 3 x 2 x 5 = 30m³

Question 4.
What will be the height of a cuboid of volume 168 m³, if the area of its base is 28 m² ?
Solution:
Volume of a cuboid = 168 m³
Area of its base l.e., l x b = 28 m³

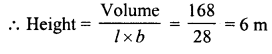
Question 5.
A tank is 8 m long, 6 m broad and 2 m high. How much water can it contain ?
Solution:
Length of tank (l) = 8 m
Breadth (b) = 6 m
Height (h) = 2 m
∴ Volume of water in the tank = l x b x h = 8 x 6 x 2 = 96 m³
= 96 x 1000 = 96000litres (∵1m³ = 1000litre)

Question 6.
The capacity of a certain cuboidal tank is 50000 litres of water. Find the breadth of the tank if its height and length are 10 m and 2.5 m respectively.
Solution:
Capacity of water in the tank = 50000 litres
∴ Volume of water = 50000 x \(\frac { 1 }{ 1000 }\) = 50 m³ (1000 l = 1 m³)
Height of tank (h)= 10 m
and length (l) = 2.5 m
Volume 50

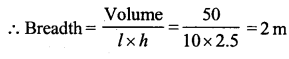
Question 7.
A rectangular diesel tanker is 2 m long, 2 m wide and 40 cm deep. How many litres of diesel can it hold ?
Solution:
Length of tanker (l) = 2 m
Breadth (b) = 2m
Depth (h) = 40 cm = 0.4 m
∴ Volume = l x bx h = 2 x 2 x 0.4=1.6m³
Quantity of diesel = 1.6 x 1000 litres (1 m³= 1000 l)
= 1600 litres

Question 8.
The length, breadth and height of a room are 5 m, 4.5 m and 3 m, respectively. Find the volume of the air it contains.
Solution:
Length of room (l) = 5 m
Breadth (6) = 4.5 m
and height (h) = 3 m
∴ Volume of air it contains
= l x b x h = 5 x 4.5 x 3 m³
= 67.5 m³

Question 9.
A water tank is 3 m long, 2 m broad and 1 m deep. How many litres of water can it hold ?
Solution:
Length of tank (l) = 3 m
Breadth (b) = 2 m
and depth (h) = 1 m
∴ Volume of tank = l x b x h
= 3 x 2 x 1 = 6 m³
∴ Quantity of water it can contains
= 6 x 1000 litres = 6000 litres (1 m³= 1000 litres)

Question 10.
How many planks each of which is 3 m long, 15 cm broad and 5 cm thick can be prepared from a wooden block 6 m long, 75 cm broad and 45 cm thick ?
Solution:
Length of wooden block (l) = 6 m
Width (b) = 75 cm = 0.75 m
Thickness (h) = 45 cm = 0.45 m
∴ Volume = l x b x h = 6 x 0.75 x 0.45 m³
Length of plank (l) = 3 m
Breadth (b) = 15 cm = 0.15 m
Thickness (h) = 5 cm = 0.05 m
∴ Volume = 3 x 0.15 x 0.05 m³
Number of planks

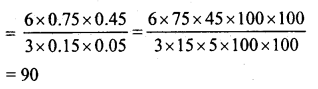
Question 11.
How many bricks each of size 25 cm x 10 cm x 8 cm will be required to build a wall 5 m long, 3 m high and 16 cm thick assuming that the volume of sand and cement used in the construction is negligible ?
Solution:
Size of one brick = 25 cm x 10 cm x 8 cm
∴ Volume of one brick = 25 x 10 x 8 cm³

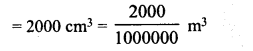
Length of wall (l) = 5 m
Width (b) = 0.16 m
Height (h) = 3 m
∴ Volume of wall = l x b x h
= 5 x 0.16 x 3 m³ = 2.4 m³
∴ Number of bricks required

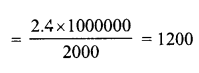
Question 12.
A village, having a population of 4000 requires 150 litres water per head per day. It has a tank which is 20 m long, 15 m broad and 6 m high. For how many days the water of this tank will last ?
Solution:
Total population of a village = 4000
Water required for each person for one day = 150 litres
∴ Water required for 4000 persons for one day = 150 x 4000 = 600000 litres
Length of tank (l) = 20 m
Breadth (b) = 15 m
Height (h) = 6 m
∴ Volume of tank = l x b x h = 20 x 15 x 6 m³ = 1800 m³
Capacity of water in the tank = 1800 x 1000 l= 1800000l (1 m³ = 1000 l)
∴ Number of days, the water will last

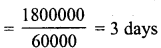
Question 13.
A rectangular field is 70 m long and 60 m broad. A well of dimensions 14 m x 8 m x 6 m is dug outside the field and the earth dugout from this well is spread evenly on the field. How much will the earth level rise ?
Solution:
Length of well (l) = 14 m
Breadth (A) = 8m
Depth (A) = 6m
∴ Volume of earth dugout = l x bx h
= 14 x 8 x 6 = 672 m³ Length of field = 70 m
and breadth = 60 m
Let h be the height of earth spread over
Then 70 x 60 x h = 672
⇒ h = \(\frac { 672 }{ 70×60 }\) = 0.16m
∴ Height of earth = 0.16 m = 16 cm

Question 14.
A swimming pool is 250 m long and 130 m wide. 3250 cubic metres of water is pumped into it. Find the rise in the level of water.
Solution:
Volume of water = 3250 m³
Length of pool (l) = 250 m
Breadth (b)= 130 m
∴ Height of water level

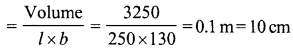
Question 15.
A beam 5 m long and 40 cm wide contains 0.6 cubic metres of wood. How thick is the beam?
Solution:
Volume of wood of the beam = 0.6 m³ = 600000
Length of beam (l) = 5 m = 500 cm
Breadth (b) = 40 cm

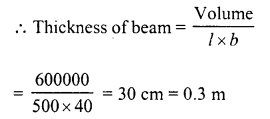
Question 16.
The rainfall on a certain day was 6 cm. How many litres of water fell on 3 hectares of field on that day ?
Solution:
Area of the field = 3 hectares
= 3 x 10000 square metres
= 30000 square metres
Height of rainfall = 6 cm = m³

Question 17.
An 8 m long cuboidal beam of wood when sliced produces four thousand 1 cm cubes and there is no wastage of wood in this process. If one edge of the beam is 0.5 m, find the third edge.
Solution:
Length of cuboidal beam (l) = 8 m = 800 cm
Number of cubical sliced = 4000
Edge of each cube = 1 cm
Volume of beam = 4000 (1)³ cm³ = 4000 cm³
One edge of the beam = 0.5 m = 50 cm.

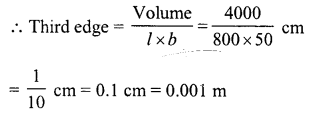
Question 18.
The dimensions of a metal block are 2.25 m by 1.5 m by 27 cm. It is melted and recast into cubes, each of the side 45 cm. How many cubes are formed ?
Solution:
Dimensions of metal block = 2.25 m x 1.5 m x 27 cm
∴ Volume = 2.25 x 1.5 x 0.27 m³
= 225 x 150 x 27 cm³ = 911250 cm³
Side of each cube (a) = 45 cm
∴ Volume of one cube = a³ = (45)³ cm³ = 91125 cm³
∴ Number of cubes = \(\frac { 911250 }{ 91125 }\) = 10

Question 19.
A solid rectangular piece of iron measures 6 m by 6 cm by 2 cm. Find the weight of this piece if 1 cm3 of iron weighs 8 gm.
Solution:
Dimensions of a piece of rectangular iron = 6m x 6cm x 2cm
∴ Volume = 600 x 6 x 2 cm³ = 7200 cm³
Weight of 1 cm³ = 8 gm
∴ Total weight of the piece = 7200 x 8 gm
= 57600 gm = \(\frac { 57600 }{ 1000 }\) kg = 57.6 kg

Question 20.
Fill in the blanks in each of the following so as to make the statement true :
(i) 1 m³ = ……… cm³
(ii) 1 litre = …….. cubic decimetre
(iii) 1 kl = …… m³
(iv) The volume of a cube of side 8 cm is …….. .
(v) The volume of wooden cuboid of length 10 cm and breadth 8 cm is 4000 cm3. The height of the cuboid is …….. cm
(vi) 1 cu.dm = …….. cu.mm
(vii) 1 cu.km = ……cu.m
(viii) 1 litre =…….. cu.cm
(ix) 1 ml = ……… cu.cm
(x) 1 kl = ……… cu.dm = ……. cu.cm.
Solution:
(i) 1 m³ = 1000000 or 10⁶ cm³
(ii) 1 litre = 1 cubic decimetre
(iii) 1 kl = 1 m³
(iv) The volume of a cube of side 8 cm is 512 cm³ (V = a³ = 8 x 8 x 8 = 512 cm³)
(v) The volume of a wooden cuboid of length 10 cm and breadth 8 cm is 4000 cm³. The height of the cuboid is 50 cm

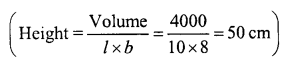
(vi) 1 cu.dm = 1000000 cu mm = 10⁶ cu.mm
(vii) 1 cu.km = 1000 x 1000 x 1000 cu.m = 109 cu.m
(viii) 1 litre = 1000 cu.cm = 10³ cu.cm
(ix) 1 ml = 1 cu.cm
(x) 1 kl = 1000 cu.dm = 100 x 100 x 100 cu.cm = 10⁶ cu.cm

Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.